湘教版九年级下册数学 1.2.5 二次函数y=ax2+bx+c(a≠0)的图象与性质 课件(共23张PPT)
文档属性
| 名称 | 湘教版九年级下册数学 1.2.5 二次函数y=ax2+bx+c(a≠0)的图象与性质 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第一章 二次函数 1.2
二次函数的图象与性质
湘教版(2024)九年级下册数学课件
1.2.5 二次函数y=ax +bx+c
(a≠0)的图象与性质
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
画出 的图象.
配方:
故对称轴是直线 ,
顶点坐标是 .
新课讲解
列表:自变量 x 从顶点的横坐标 开始取值.
x …
…
新课讲解
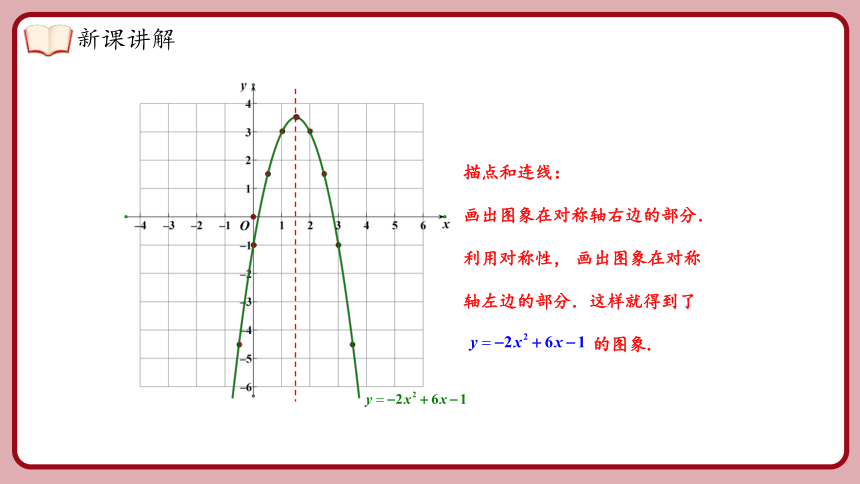
描点和连线:
画出图象在对称轴右边的部分.
利用对称性, 画出图象在对称轴左边的部分.这样就得到了
的图象.
新课讲解
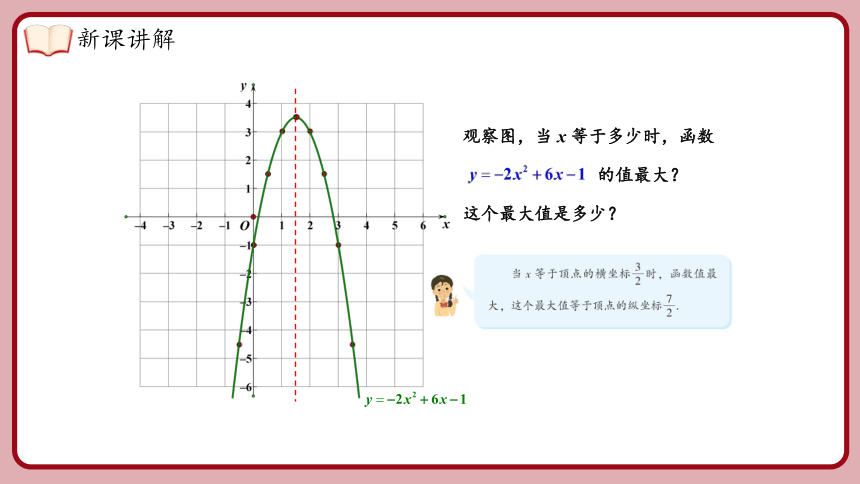
观察图,当 x 等于多少时,函数
的值最大?
这个最大值是多少?
新课讲解
一般地, 有下述结论:
二次函数 y = ax2 + bx + c, 当 x 等于顶点的横坐标时, 达到最大值(a < 0 )或最小值(a > 0 ), 这个最大(小)值等于顶点的纵坐标.
新课讲解
求二次函数 的最大值.
解 配方:
顶点坐标(2,1),于是当 x = 2 时,y达到最大值 1.
【教材P17页】
新课讲解
根据下列关系你能发现二次函数 y=ax2+bx+c 的图象和性质吗?
y = ax2 + bx + c
顶点坐标是
因此,当 时,函数达到最大值(a < 0)或
最小值(a > 0):
新课讲解
1. 写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1) ;
(2) .
(1)对称轴 x = 1,顶点坐标(1,-2),开口向上
(2)对称轴 x = 2,顶点坐标(2,2),开口向下
【教材P18页】
新课讲解
1. 写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1) ;
(2) .
【教材P18页】
新课讲解
2. 求下列二次函数图象的顶点坐标以及最大值或
最小值:
(1) ; (2)
(1)
顶点坐标
最小值
(2)
顶点坐标(-3,4)
最大值 4
【教材P18页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
将二次函数 y = x2+2x-1 的图象沿 x 轴向右平移 2 个单位, 得到的函数表达式是( )
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x-1)2+2
D.y=(x-1)2-2
D
课堂练习
2. 已知二次函数 y = a(x -1)2+b (a ≠ 0)有最小值-1,
则 a 与 b 之间的大小关系是( )
A.a<b B.a = b
C.a>b D.不能确定
C
课堂练习
3. 若一次函数 y = (a+1) x+a 的图象过第一、三、四象限,
则二次函数 y=ax2-ax( )
A.有最大值
B.有最大值-
C.有最小值
D.有最小值-
B
课堂练习
4. 已知抛物线 y=-x2+2x+2.
(1)通过配方求出它的对称轴、顶点坐标,并画出该抛物线;
(2)若该抛物线上两点 A (x1 , y1), B(x2 , y2)的横坐标满足 x1>x2>1,
试比较 y1 与 y2 的大小.
解:(1)配方:y =-x2+2x+2
=-(x-1)2+3
对称轴是直线 x = 1,顶点坐标是(1,3)
(2)y1 < y2
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
用配方法求二次函数 y = ax2 + bx + c 的顶点坐标、对称轴;
y = ax2 + bx + c
课堂小结
二次函数 y = ax2 + bx + c 的图象特征与系数 a,b,c及b2-4ac 的符号之间的关系:
课堂小结
第一章 二次函数 1.2
二次函数的图象与性质
湘教版(2024)九年级下册数学课件
1.2.5 二次函数y=ax +bx+c
(a≠0)的图象与性质
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
画出 的图象.
配方:
故对称轴是直线 ,
顶点坐标是 .
新课讲解
列表:自变量 x 从顶点的横坐标 开始取值.
x …
…
新课讲解
描点和连线:
画出图象在对称轴右边的部分.
利用对称性, 画出图象在对称轴左边的部分.这样就得到了
的图象.
新课讲解
观察图,当 x 等于多少时,函数
的值最大?
这个最大值是多少?
新课讲解
一般地, 有下述结论:
二次函数 y = ax2 + bx + c, 当 x 等于顶点的横坐标时, 达到最大值(a < 0 )或最小值(a > 0 ), 这个最大(小)值等于顶点的纵坐标.
新课讲解
求二次函数 的最大值.
解 配方:
顶点坐标(2,1),于是当 x = 2 时,y达到最大值 1.
【教材P17页】
新课讲解
根据下列关系你能发现二次函数 y=ax2+bx+c 的图象和性质吗?
y = ax2 + bx + c
顶点坐标是
因此,当 时,函数达到最大值(a < 0)或
最小值(a > 0):
新课讲解
1. 写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1) ;
(2) .
(1)对称轴 x = 1,顶点坐标(1,-2),开口向上
(2)对称轴 x = 2,顶点坐标(2,2),开口向下
【教材P18页】
新课讲解
1. 写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1) ;
(2) .
【教材P18页】
新课讲解
2. 求下列二次函数图象的顶点坐标以及最大值或
最小值:
(1) ; (2)
(1)
顶点坐标
最小值
(2)
顶点坐标(-3,4)
最大值 4
【教材P18页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
将二次函数 y = x2+2x-1 的图象沿 x 轴向右平移 2 个单位, 得到的函数表达式是( )
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x-1)2+2
D.y=(x-1)2-2
D
课堂练习
2. 已知二次函数 y = a(x -1)2+b (a ≠ 0)有最小值-1,
则 a 与 b 之间的大小关系是( )
A.a<b B.a = b
C.a>b D.不能确定
C
课堂练习
3. 若一次函数 y = (a+1) x+a 的图象过第一、三、四象限,
则二次函数 y=ax2-ax( )
A.有最大值
B.有最大值-
C.有最小值
D.有最小值-
B
课堂练习
4. 已知抛物线 y=-x2+2x+2.
(1)通过配方求出它的对称轴、顶点坐标,并画出该抛物线;
(2)若该抛物线上两点 A (x1 , y1), B(x2 , y2)的横坐标满足 x1>x2>1,
试比较 y1 与 y2 的大小.
解:(1)配方:y =-x2+2x+2
=-(x-1)2+3
对称轴是直线 x = 1,顶点坐标是(1,3)
(2)y1 < y2
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
用配方法求二次函数 y = ax2 + bx + c 的顶点坐标、对称轴;
y = ax2 + bx + c
课堂小结
二次函数 y = ax2 + bx + c 的图象特征与系数 a,b,c及b2-4ac 的符号之间的关系:
课堂小结
