人教版九下数学 26.2.1 实际问题与反比例函数1 课件 (共20张PPT)
文档属性
| 名称 | 人教版九下数学 26.2.1 实际问题与反比例函数1 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
人教版九年级数学下册课件
第二十六章 反比例函数
实际问题与反比例函数1
26.2.1
复习巩固
01
新课导入
02
课堂检测
03
延伸拓展
04
目
录
复习巩固
01
学习目标
重点难点
前言
1、运用反比例函数的知识解决实际问题。
2、经历“实际问题-建立模型-拓展应用”的过程,发展学生分析、解决问题的能力。
3、经历运用反比例函数解决实际问题的过程,体会数学建模的思想。
运用反比例函数解决实际问题。
把实际问题转化为反比例函数。
新课导入
02
BY YUSHEN
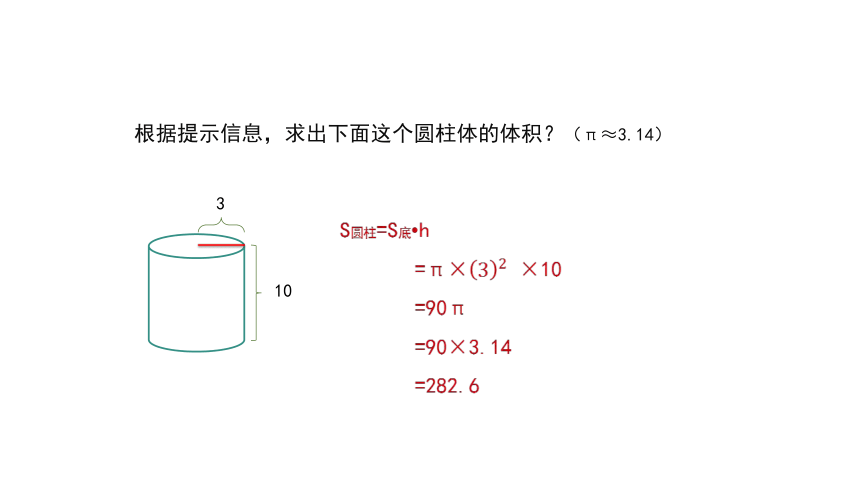
根据提示信息,求出下面这个圆柱体的体积?(π≈3.14)
3
10
S圆柱=S底 h
=π× ×10
=90π
=90×3.14
=282.6
新知探究
BY YUSHEN
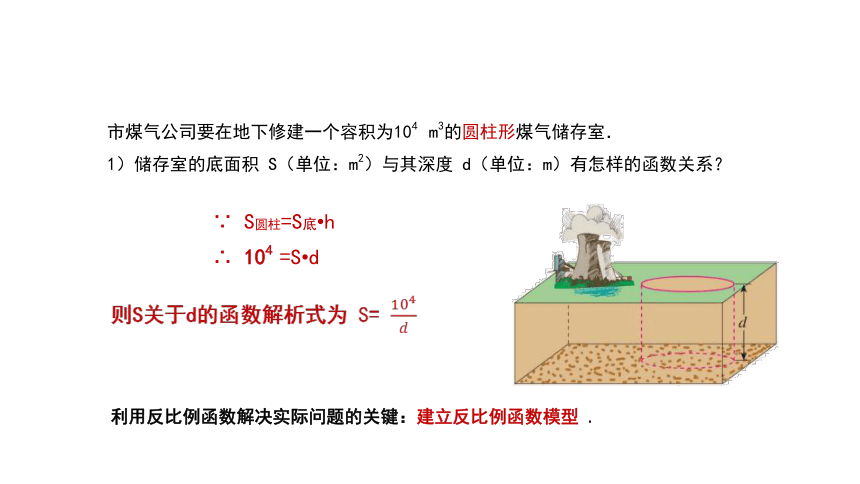
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
1)储存室的底面积 S(单位:m2)与其深度 d(单位:m)有怎样的函数关系?
∵ S圆柱=S底 h
∴ 104 =S d
则S关于d的函数解析式为 S=
利用反比例函数解决实际问题的关键:建立反比例函数模型 .
新知探究
BY YUSHEN
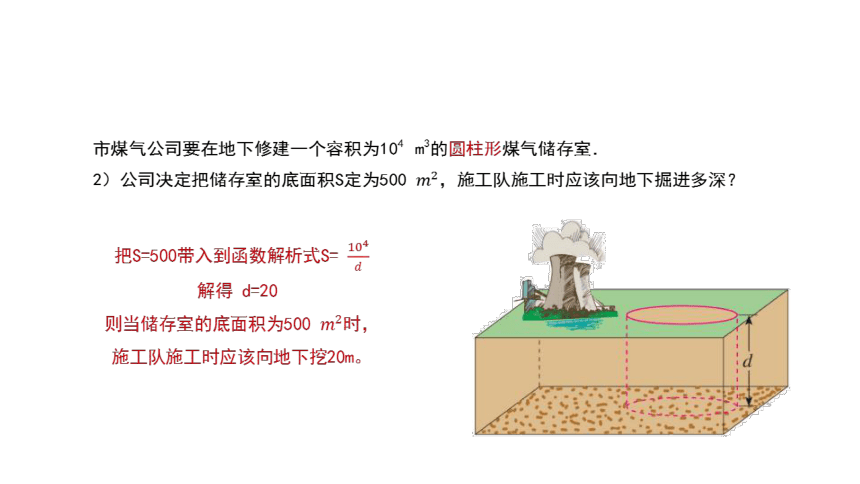
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
2)公司决定把储存室的底面积S定为500 ,施工队施工时应该向地下掘进多深?
把S=500带入到函数解析式S=
解得 d=20
则当储存室的底面积为500 时,
施工队施工时应该向地下挖20m。
新知探究
BY YUSHEN
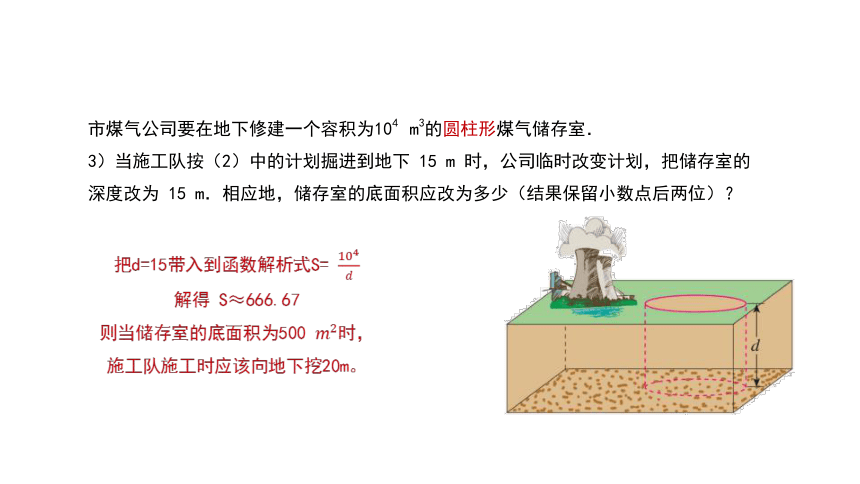
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
3)当施工队按(2)中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
把d=15带入到函数解析式S=
解得 S≈666.67
则当储存室的底面积为500 时,
施工队施工时应该向地下挖20m。
新知探究
BY YUSHEN
1.根据题意找等量关系
2.列出方程,并注明自变量的取值范围
3.解方程
4.写答案
新知探究
实际问题与反比例函数的解题步骤
BY YUSHEN
码头工人每天往一艘轮船上装载30 吨货物,装载完毕恰好用了 8 天时间.
1)轮船到达目的地后开始卸货,平均卸货速度 v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
等量关系:
每日装载量×装载天数=货物的总量
货物的总量÷卸货天数=每日卸货速度
1)解:设货物总量为k吨
k=30×8=240
则v关于t的函数解析式为 v=
新知探究
BY YUSHEN
码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
把t=5带入到函数解析式v=
解得 v=48
若正好5天卸货完毕,则平均每天卸货48吨。
而vt=240(t>0),t的值越小,v的值越大。
则若t≤5,v≥48
这样按照5天卸载完毕,那么平均每天至少要卸载48吨
新知探究
课堂检测
03
BY YUSHEN
1.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ与体积V是反比例函数关系,它的图象如图所示.
(1)求密度ρ关于体积V的函数解析式;
(2)当密度ρ不低于4kg/m3时,求二氧化碳体积的取值范围。
解:设密度ρ与体积V的反比例函数解析式为ρ=,
把点(6,2)代入解ρ=,得k=12,
∴密度ρ与体积V的反比例函数解析式为ρ=(v>0);
(2)由图象得:当ρ≥4时,0<v≤3,
答:当密度ρ不低于4kg/m3时,二氧化碳体积的取值范围是0<v≤3.
课堂练习
BY YUSHEN
2.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:)是体积(单位:)的反比例函数,它的图象如图所示:
1)求与之间的函数关系式,并写出自变量的取值范围;
2)求当时气体的密度.
解:1)设密度ρ与体积V的反比例函数解析式为ρ=,
把点(5,2)代入解ρ=,得k=10,
∴密度ρ与体积V的反比例函数解析式为.
2)把v=10m3代入,得ρ=1.
课堂练习
BY YUSHEN
3.一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
2)如果提速后平均速度为78km/h,求提速后全程运营时间;
3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
1)解:由题意可得,总路程为58×65=3770(km),
则提速后平均速度为vkm/h,全程运营时间为t小时,
故t与v之间的函数表达式为:t=
等量关系:路程=速度×时间
课堂练习
BY YUSHEN
(2)当v=78km/h时,t==48(小时),
答:提速后全程运营时间为48小时;
(3)∵全程运营的时间控制在40h内,
∴平均速度应为:t ≥ =94.25,
答:提速后,平均速度至少应为94.25km.
课堂练习
延伸拓展
04
BY YUSHEN
4.“聚能”电厂现在有5000吨煤.
(1) 这些煤能够使用的天数y(单位:天)与该厂平均每天用煤吨数x(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
1)解:由题意可得,现存煤炭量为5000吨
故x与y之间的函数表达式为:y=
2)把x=200带入y=中得,y=25 答:每天用200吨,可用25天。
等量关系:现存煤炭量=每天用煤吨数×天数
课堂练习
BY YUSHEN
3)前10天用煤量为 10×200=2000(吨)
剩余煤炭量为5000-2000=3000(吨)
后续每天用煤300吨,则
3000÷300=10(天)
答:这批煤共可用20天
4.“聚能”电厂现在有5000吨煤.
(1) 这些煤能够使用的天数y(单位:天)与该厂平均每天用煤吨数x(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
课堂练习
人教版九年级数学下册课件
第二十六章 反比例函数
实际问题与反比例函数1
26.2.1
复习巩固
01
新课导入
02
课堂检测
03
延伸拓展
04
目
录
复习巩固
01
学习目标
重点难点
前言
1、运用反比例函数的知识解决实际问题。
2、经历“实际问题-建立模型-拓展应用”的过程,发展学生分析、解决问题的能力。
3、经历运用反比例函数解决实际问题的过程,体会数学建模的思想。
运用反比例函数解决实际问题。
把实际问题转化为反比例函数。
新课导入
02
BY YUSHEN
根据提示信息,求出下面这个圆柱体的体积?(π≈3.14)
3
10
S圆柱=S底 h
=π× ×10
=90π
=90×3.14
=282.6
新知探究
BY YUSHEN
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
1)储存室的底面积 S(单位:m2)与其深度 d(单位:m)有怎样的函数关系?
∵ S圆柱=S底 h
∴ 104 =S d
则S关于d的函数解析式为 S=
利用反比例函数解决实际问题的关键:建立反比例函数模型 .
新知探究
BY YUSHEN
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
2)公司决定把储存室的底面积S定为500 ,施工队施工时应该向地下掘进多深?
把S=500带入到函数解析式S=
解得 d=20
则当储存室的底面积为500 时,
施工队施工时应该向地下挖20m。
新知探究
BY YUSHEN
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
3)当施工队按(2)中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
把d=15带入到函数解析式S=
解得 S≈666.67
则当储存室的底面积为500 时,
施工队施工时应该向地下挖20m。
新知探究
BY YUSHEN
1.根据题意找等量关系
2.列出方程,并注明自变量的取值范围
3.解方程
4.写答案
新知探究
实际问题与反比例函数的解题步骤
BY YUSHEN
码头工人每天往一艘轮船上装载30 吨货物,装载完毕恰好用了 8 天时间.
1)轮船到达目的地后开始卸货,平均卸货速度 v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
等量关系:
每日装载量×装载天数=货物的总量
货物的总量÷卸货天数=每日卸货速度
1)解:设货物总量为k吨
k=30×8=240
则v关于t的函数解析式为 v=
新知探究
BY YUSHEN
码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
把t=5带入到函数解析式v=
解得 v=48
若正好5天卸货完毕,则平均每天卸货48吨。
而vt=240(t>0),t的值越小,v的值越大。
则若t≤5,v≥48
这样按照5天卸载完毕,那么平均每天至少要卸载48吨
新知探究
课堂检测
03
BY YUSHEN
1.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ与体积V是反比例函数关系,它的图象如图所示.
(1)求密度ρ关于体积V的函数解析式;
(2)当密度ρ不低于4kg/m3时,求二氧化碳体积的取值范围。
解:设密度ρ与体积V的反比例函数解析式为ρ=,
把点(6,2)代入解ρ=,得k=12,
∴密度ρ与体积V的反比例函数解析式为ρ=(v>0);
(2)由图象得:当ρ≥4时,0<v≤3,
答:当密度ρ不低于4kg/m3时,二氧化碳体积的取值范围是0<v≤3.
课堂练习
BY YUSHEN
2.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:)是体积(单位:)的反比例函数,它的图象如图所示:
1)求与之间的函数关系式,并写出自变量的取值范围;
2)求当时气体的密度.
解:1)设密度ρ与体积V的反比例函数解析式为ρ=,
把点(5,2)代入解ρ=,得k=10,
∴密度ρ与体积V的反比例函数解析式为.
2)把v=10m3代入,得ρ=1.
课堂练习
BY YUSHEN
3.一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
2)如果提速后平均速度为78km/h,求提速后全程运营时间;
3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
1)解:由题意可得,总路程为58×65=3770(km),
则提速后平均速度为vkm/h,全程运营时间为t小时,
故t与v之间的函数表达式为:t=
等量关系:路程=速度×时间
课堂练习
BY YUSHEN
(2)当v=78km/h时,t==48(小时),
答:提速后全程运营时间为48小时;
(3)∵全程运营的时间控制在40h内,
∴平均速度应为:t ≥ =94.25,
答:提速后,平均速度至少应为94.25km.
课堂练习
延伸拓展
04
BY YUSHEN
4.“聚能”电厂现在有5000吨煤.
(1) 这些煤能够使用的天数y(单位:天)与该厂平均每天用煤吨数x(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
1)解:由题意可得,现存煤炭量为5000吨
故x与y之间的函数表达式为:y=
2)把x=200带入y=中得,y=25 答:每天用200吨,可用25天。
等量关系:现存煤炭量=每天用煤吨数×天数
课堂练习
BY YUSHEN
3)前10天用煤量为 10×200=2000(吨)
剩余煤炭量为5000-2000=3000(吨)
后续每天用煤300吨,则
3000÷300=10(天)
答:这批煤共可用20天
4.“聚能”电厂现在有5000吨煤.
(1) 这些煤能够使用的天数y(单位:天)与该厂平均每天用煤吨数x(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
课堂练习
