【浙教版】2024-2025学年第二学期七年级数学期中模拟试卷(1)(含解析)
文档属性
| 名称 | 【浙教版】2024-2025学年第二学期七年级数学期中模拟试卷(1)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 817.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年第二学期七年级数学期中模拟试卷(1)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列是二元一次方程的是( )
A.3x﹣6y B.2x﹣3y=x2 C. D.3x﹣2y=0
2.华为麒麟9000处理器采用了5nm工艺制程,5nm=0.000000005m.把数0.000000005用科学记数法表示,记为( )
A.0.5×10﹣9 B.5×10﹣8 C.5×10﹣9 D.0.5×10﹣8
3.如图,直线a、b被直线c所截,则∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.如图,直线AB,CD被直线CE所截,AB∥CD,∠1=140°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
5.下列各运算中,计算正确的是( )
A.x3 (﹣x)2=x5 B.(﹣2x2)3=﹣6x6 C.a6÷a3=a2 D.(x﹣2)2=x2﹣4
6.若是方程2x+3y=﹣1的一个解,则6a+9b+4的值是( )
A.﹣2 B.1 C.3 D.7
7.若am=4,an=2,则a2m﹣n的值为( )
A.8 B.12 C.24 D.48
8.若是方程组的解,则a2﹣b2的值为( )
A. B. C.﹣16 D.16
9.盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )
A. B. C. D.
10.如图,图①所示的小长方形两条边的长分别为1,m(m>1),现将这样5个大小形状完全相同的小长方形不重叠地放入图②所示的大长方形中,图中未被覆盖部分用阴影表示,其面积分别为S1,S2.设面积为S1的长方形一条边为x.若无论x为何值,图中阴影部分S1﹣S2的值总保持不变,此时S1﹣S2的值为( )
A. B.2 C. D.3
二、填空题:本题共6小题,每小题3分,共18分。
11.计算:3x3 (﹣x)2= .
12.已知4x﹣y=3,用含x的代数式表示y,则y= .
13.如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加 (只填出一种即可)的条件.
14.如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于 .
15.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,阴影部分的面积为48,则平移距离为 .
16.若方程组的解是,则方程组的解是 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.因式分解:
(1)8abc﹣2bc2; (2)2x(x+y)﹣6(x+y).
18.计算:
(1)+(﹣1)2023+(π﹣3.14)0﹣|﹣3|; (2)(﹣2x2)3+x2 x4﹣(﹣3x3)2.
19.解方程组:
(1); (2).
20.先化简,再求值:[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷2x,其中x=3,y=﹣1.
21.如图,在所给4×4网格图(每个小格均为边长是1的正方形)中完成下列各题:
(1)△ABC的面积为 ;
(2)按下列要求作格点三角形(图形的顶点都在正方形格纸的格点上).
①在图1中,将△ABC平移,得到△A′B′C′,请画一个△A′B′C′与△ABC无重合部分.
②在图2中,线段AB与CD相交,产生∠α,请画一个△ABE,使得△ABE中的一个角等于∠α.
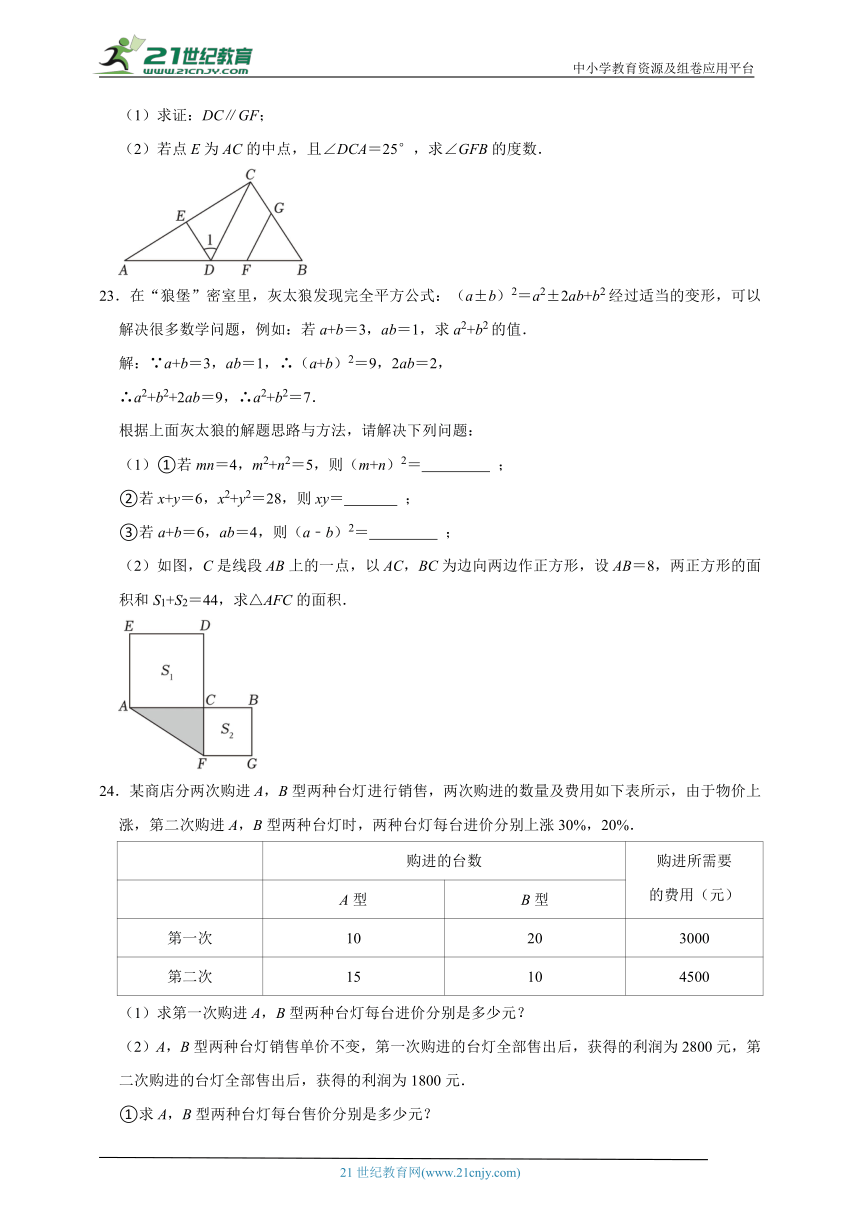
22.如图,在△ABC中,∠ACB=90°,点D,F在边AB上,过点D作DE∥BC交AC于点E,G为BC上一点,连接FG,且∠1+∠CGF=180°.
(1)求证:DC∥GF;
(2)若点E为AC的中点,且∠DCA=25°,求∠GFB的度数.
23.在“狼堡”密室里,灰太狼发现完全平方公式:(a±b)2=a2±2ab+b2经过适当的变形,可以解决很多数学问题,例如:若a+b=3,ab=1,求a2+b2的值.
解:∵a+b=3,ab=1,∴(a+b)2=9,2ab=2,
∴a2+b2+2ab=9,∴a2+b2=7.
根据上面灰太狼的解题思路与方法,请解决下列问题:
(1)①若mn=4,m2+n2=5,则(m+n)2= ;
②若x+y=6,x2+y2=28,则xy= ;
③若a+b=6,ab=4,则(a﹣b)2= ;
(2)如图,C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=44,求△AFC的面积.
24.某商店分两次购进A,B型两种台灯进行销售,两次购进的数量及费用如下表所示,由于物价上涨,第二次购进A,B型两种台灯时,两种台灯每台进价分别上涨30%,20%.
购进的台数 购进所需要的费用(元)
A型 B型
第一次 10 20 3000
第二次 15 10 4500
(1)求第一次购进A,B型两种台灯每台进价分别是多少元?
(2)A,B型两种台灯销售单价不变,第一次购进的台灯全部售出后,获得的利润为2800元,第二次购进的台灯全部售出后,获得的利润为1800元.
①求A,B型两种台灯每台售价分别是多少元?
②若按照第二次购进A,B型两种台灯的价格再购进一次,将再次购进的台灯全部售出后,要想使获得的利润为1000元,求有哪几种购进方案?
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列是二元一次方程的是( )
A.3x﹣6y B.2x﹣3y=x2 C. D.3x﹣2y=0
【点拨】利用二元一次方程的定义,逐一分析四个选项中的方程,即可得出结论.
【解答】解:A.方程3x﹣6不是一元一次方程,选项A不符合题意;
B.方程2x﹣3y=x2是二元二次方程,选项B不符合题意;
C.方程2x﹣=1是分式方程,选项C不符合题意;
D.方程3x﹣2y=0是二元一次方程,选项D符合题意.
故选:D.
【点睛】本题考查了二元一次方程的定义,牢记“含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程”是解题的关键.
2.华为麒麟9000处理器采用了5nm工艺制程,5nm=0.000000005m.把数0.000000005用科学记数法表示,记为( )
A.0.5×10﹣9 B.5×10﹣8 C.5×10﹣9 D.0.5×10﹣8
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:0.000000005=5×10﹣9.
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.如图,直线a、b被直线c所截,则∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【点拨】根据内错角的定义求解.
【解答】解:∠1的内错角是∠3.
故选:B.
【点睛】本题主要考查了同位角、内错角、同旁内角,对顶角、邻补角,关键掌握两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
4.如图,直线AB,CD被直线CE所截,AB∥CD,∠1=140°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
【点拨】先根据补角的定义得出∠AEC的度数,再由平行线的性质即可得出结论.
【解答】解:∵∠1=140°,
∴∠AEC=180°﹣140°=40°,
∵AB∥CD,
∴∠C=∠AEC=40°.
故选:B.
【点睛】本题考查的是平行线的性质,熟知两直线平行,内错角相等是解题的关键.
5.下列各运算中,计算正确的是( )
A.x3 (﹣x)2=x5 B.(﹣2x2)3=﹣6x6 C.a6÷a3=a2 D.(x﹣2)2=x2﹣4
【点拨】利用完全平方公式,同底数幂的乘除法运算法则以及积的乘方分别分析得出即可.
【解答】解:A、x3 (﹣x)2=x5,故正确,符合题意;
B、(﹣2x2)3=﹣8x6,故故错误,不符合题意;
C、x6÷x3=x3,故错误,不符合题意;
D、(x﹣2)2=x2﹣4x+4,故错误,不符合题意.
故选:A.
【点睛】此题主要考查了完全平方公式,同底数幂的乘除法,幂的乘方与积的乘方,掌握相应的运算法则是解题关键.
6.若是方程2x+3y=﹣1的一个解,则6a+9b+4的值是( )
A.﹣2 B.1 C.3 D.7
【点拨】将x=a,y=b代入方程2x+3y=﹣1,得,2a+3b=﹣1,可得6a+9b=﹣3,即得6a+9b+4的值.
【解答】解:将x=a,y=b代入方程2x+3y=﹣1,
得,2a+3b=﹣1,
∴6a+9b=﹣3,
∴6a+9b+4=1,
故选:B.
【点睛】本题考查了二元一次方程的解,将方程的一个解x=a,y=b代入方程求得2a+3b的值是本题的关键.
7.若am=4,an=2,则a2m﹣n的值为( )
A.8 B.12 C.24 D.48
【点拨】利用幂的乘方与积的乘方的法则,同底数幂的除法法则进行计算,即可得出答案.
【解答】解:∵am=4,an=2,
∴a2m﹣n
=a2m÷an
=(am)2÷an
=42÷2
=16÷2
=8,
故选:A.
【点睛】本题考查了幂的乘方与积的乘方,同底数幂的除法,掌握幂的乘方与积的乘方的法则,同底数幂的除法法则是解决问题的关键.
8.若是方程组的解,则a2﹣b2的值为( )
A. B. C.﹣16 D.16
【点拨】把代入原方程组得,解出a+b与a﹣b,再进一步即可求出答案.
【解答】解:把代入原方程组
得,
∴两个方程相加得:3a+3b=8即,
两个方程相减得:a﹣b=6,
∴,
故选:D.
【点睛】本题考查了二元一次方程和利用平方差公式分解因式,学生们熟练掌握二元一次方程的计算和平方差公式的计算即可.
9.盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )
A. B. C. D.
【点拨】设用x米布料做玩偶A,用y米布料做玩偶B,根据等量关系式:玩偶A的个数×2=玩偶B的个数,玩偶A用的布料+玩偶B用的布料=136米,列出方程组即可.
【解答】解:设用x米布料做玩偶A,用y米布料做玩偶B,由题意可得,
,故C正确.
故选:C.
【点睛】本题主要考查了二元一次方程组的应用,根据题意找出题目中的等量关系式,是解题的关键.
10.如图,图①所示的小长方形两条边的长分别为1,m(m>1),现将这样5个大小形状完全相同的小长方形不重叠地放入图②所示的大长方形中,图中未被覆盖部分用阴影表示,其面积分别为S1,S2.设面积为S1的长方形一条边为x.若无论x为何值,图中阴影部分S1﹣S2的值总保持不变,此时S1﹣S2的值为( )
A. B.2 C. D.3
【点拨】由题意可得图②中AB=m+3,BC=x+2,由此表示出阴影部分S1﹣S2的面积,然后令含x的项的系数之和为0,列方程求得m的值,从而求解.
【解答】解:由题意可得:AB=m+3,BC=x+2,
∴S1﹣S2=xm﹣3(x+2﹣m)
=xm﹣3x﹣6+3m
=(m﹣3)x﹣6+3m,
又∵阴影部分S1﹣S2的值总保持不变,
∴m﹣3=0,
解得:m=3,
∴S1﹣S2=﹣6+3×3=3,
故选:D.
【点睛】本题考查整式加减运算的应用,准确识图,用含x和m的式子表示出S1﹣S2是解题关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.计算:3x3 (﹣x)2= 3x5 .
【点拨】先根据积的乘方法则计算乘方,再根据单项式乘单项式法则计算乘法即可.
【解答】解:原式=3x3 x2
=3x5,
故答案为:3x5.
【点睛】本题主要考查了整式的混合运算,解题关键是熟练掌握积的乘方法则、同底数幂相乘法则和单项式乘单项式法则.
12.已知4x﹣y=3,用含x的代数式表示y,则y= 4x﹣3 .
【点拨】根据等式的性质解答即可.
【解答】解:4x﹣y=3,
等式两边同时加上y,得4x﹣y+y=3+y,即4x=3+y,
等式两边同时减去3,得4x﹣3=3+y﹣3,
∴y=4x﹣3,
故答案为:y=4x﹣3.
【点睛】本题考查了等式的性质,二元一次方程,掌握等式的性质是解题的关键.
13.如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加 ∠ACD=90°(答案不唯一). (只填出一种即可)的条件.
【点拨】由平行线的判定,即可得到答案.
【解答】解:∵AB⊥AC,
∴∠BAC=90°,
若∠ACD=90°,则∠BAC=∠ACD,
∴AB∥CD,
∴要使AB∥CD,可添加∠ACD=90°(答案不唯一).
故答案为:∠ACD=90°(答案不唯一).
【点睛】本题考查平行线的判定,关键是掌握平行线的判定方法.
14.如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于 55° .
【点拨】利用平行线的性质及角的和差即可求得答案.
【解答】解:如图,设直角三角形的顶点分别为A,B,C,其斜边交直线b于点D,
∵直线a∥b∥c,
∴∠1=∠ACD,∠2=∠BCD,
∵∠ACD+∠BCD=90°,
∴∠1+∠2=90°,
∵∠1=35°,
∴∠2=90°﹣35°=55°,
故答案为:55°.
【点睛】本题考查平行线性质及角的计算,结合已知条件求得∠1+∠2=90°是解题的关键.
15.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,阴影部分的面积为48,则平移距离为 6 .
【点拨】根据平移的性质可知:AB=DE,由此可求出EH的长.由S阴影DHCF=S梯形ABEH结合梯形的面积公式即可求出BE.
【解答】解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DE=AB=10,DE∥AB,S△ABC=S△DEF,
∴EH=10﹣4=6,S阴影DHCF=S梯形ABEH=48,
∴(EH+AB)BE=48,
∴(6+10)BE=48,
∴BE=6,即平移的距离为6.
故答案为:6.
【点睛】本题考查了平移的性质,对应点连线的长度等于平移距离,平移变化只改变图形的位置不改变图形的形状,熟记各性质并判断出阴影部分面积等于梯形ABEH的面积是解题的关键.
16.若方程组的解是,则方程组的解是 .
【点拨】仿照已知方程组的解确定出所求方程组的解即可.
【解答】解:∵方程组的解是,
∴方程组的解是,即.
故答案为:.
【点睛】此题考查了二次一次方程组的解,以及解二元一次方程组,利用了类比的思想,熟练掌握运算法则是解本题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.因式分解:
(1)8abc﹣2bc2; (2)2x(x+y)﹣6(x+y).
【点拨】(1)提公因式法因式分解;
(2)提公因式法因式分解.
【解答】解:(1)8abc﹣2bc2=2bc(4a﹣c);
(2)2x(x+y)﹣6(x+y)=2(x+y)(x﹣3).
【点睛】本题考查了因式分解﹣提公因式法,解题的关键是掌握因式分解的方法.
18.计算:
(1)+(﹣1)2023+(π﹣3.14)0﹣|﹣3|;
(2)(﹣2x2)3+x2 x4﹣(﹣3x3)2.
【点拨】(1)先化简各式,然后再进行计算即可解答;
(2)先算乘方,再算乘法,后算加减,即可解答.
【解答】解:(1)+(﹣1)2023+(π﹣3.14)0﹣|﹣3|
=4+(﹣1)+1﹣3
=3+1﹣3
=1;
(2)(﹣2x2)3+x2 x4﹣(﹣3x3)2
=﹣8x6+x6﹣9x6
=﹣16x6.
【点睛】本题考查了整式的混合运算,实数的运算,幂的乘方与积的乘方,同底数幂的乘法,零指数幂,负整数指数幂,准确熟练地进行计算是解题的关键.
19.解方程组:
(1); (2).
【点拨】(1)利用加减消元法解方程组即可;
(2)将原方程组整理后利用加减消元法解方程组即可.
【解答】解:(1),
①﹣②×3得:8y=0,
解得:y=0,
将y=0代入①得:3x=6,
解得:x=2,
故原方程组的解为;
(2)原方程组整理得,
①×3﹣②得:25y=150,
解得:y=6,
将y=6代入②得:3x﹣6=12,
解得:x=6,
故原方程组的解为.
【点睛】本题考查解二元一次方程组,熟练掌握解方程组的方法是解题的关键.
20.先化简,再求值:[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷2x,其中x=3,y=﹣1.
【点拨】先利用完全平方公式、平方差公式、多项式除以单项式法则化简整式,再代入求值.
【解答】解:[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷2x
=[9x2﹣6xy+y2﹣(x2﹣y2)﹣2y2]÷2x
=(9x2﹣6xy+y2﹣x2+y2﹣2y2)÷2x
=(8x2﹣6xy)÷2x
=4x﹣3y.
当x=3,y=﹣1时,
原式=4×3﹣3×(﹣1)
=12+3
=15.
【点睛】本题考查了整式的化简求值,掌握整式的运算法则、乘法公式等知识点是解决本题的关键.
21.如图,在所给4×4网格图(每个小格均为边长是1的正方形)中完成下列各题:
(1)△ABC的面积为 2.5 ;
(2)按下列要求作格点三角形(图形的顶点都在正方形格纸的格点上).
①在图1中,将△ABC平移,得到△A′B′C′,请画一个△A′B′C′与△ABC无重合部分.
②在图2中,线段AB与CD相交,产生∠α,请画一个△ABE,使得△ABE中的一个角等于∠α.
【点拨】(1)利用割补法求解即可;
(2)①把△ABC向右平移2个单位即可;
②把CD向右平移2个单位,C点与A点重合,则D点的对应点为E点.
【解答】解:(1),
故答案为:2.5;
(2)①如图1,△A′B′C′为所作;
②如图2,△ABE为所作.
∵AE∥CD,
∴∠A=∠α,
∴△ABE即为所求.
【点睛】本题考查了平移作图,割补法求面积,解答本题的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
22.如图,在△ABC中,∠ACB=90°,点D,F在边AB上,过点D作DE∥BC交AC于点E,G为BC上一点,连接FG,且∠1+∠CGF=180°.
(1)求证:DC∥GF;
(2)若点E为AC的中点,且∠DCA=25°,求∠GFB的度数.
【点拨】(1)先由DE∥BC得∠1=∠BCD,进而可得∠BCD+∠CGF=180°,然后根据平行线的判定可得出结论;
(2)先证DE⊥AC,进而得DE是线段AC的垂直平分线,则DC=DA,由此得∠A=∠DCA=25°,从而可求出∠ADE=65°,∠1=65°,进而得∠ADC=∠ADE+∠1=130°,由此可得∠CDB=180°﹣∠ADC=50°,然后在由(1)的结论可知DC∥GF,最后根据平行线的性质可得∠GFB的度数.
【解答】(1)证明:∵DE∥BC,
∴∠1=∠BCD,
又∵∠1+∠CGF=180°,
∴∠BCD+∠CGF=180°,
∴DC∥GF;
(2)解:∵∠ACB=90°,DE∥BC,
∴∠DEA=∠ACB=90°,
即DE⊥AC,
又∵点E为AC的中点,
∴DE是线段AC的垂直平分线,
∴DC=DA,
∴∠A=∠DCA=25°,
∴∠ADE=90°﹣∠A=65°,∠1=90°﹣∠DCA=65°,
∴∠ADC=∠ADE+∠1=130°,
∴∠CDB=180°﹣∠ADC=50°,
由(1)可知:DC∥GF,
∴∠GFB=∠CDB=50°.
【点睛】此题主要考查了平行线的判定和性质,线段垂直平分线的性质,等腰三角形的性质,直角三角形的性质等,熟练掌握平行线的判定和性质,线段垂直平分线的性质,理解等腰三角形的两个底角相等,直角三角形的两个锐角互余是解决问题的关键.
23.在“狼堡”密室里,灰太狼发现完全平方公式:(a±b)2=a2±2ab+b2经过适当的变形,可以解决很多数学问题,例如:若a+b=3,ab=1,求a2+b2的值.
解:∵a+b=3,ab=1,∴(a+b)2=9,2ab=2,
∴a2+b2+2ab=9,∴a2+b2=7.
根据上面灰太狼的解题思路与方法,请解决下列问题:
(1)①若mn=4,m2+n2=5,则(m+n)2= 13 ;
②若x+y=6,x2+y2=28,则xy= 4 ;
③若a+b=6,ab=4,则(a﹣b)2= 20 ;
(2)如图,C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=44,求△AFC的面积.
【点拨】(1)①运用完全平方公式,将mn=4,m2+n2=5代入(m+n)2=m2+2mn+n2进行求解;
②先将(x+y)2=x2+2xy+y2变形为xy=,再将x+y=6,x2+y2=28代入求解;
③先由(a±b)2=a2±2ab+b2可得(a﹣b)2=(a+b)2﹣4ab,再将a+b=6,ab=4代入求解;
(2)设AC=k,BC=l,可得k+l=8,k2+l2=44,再由完全平方公式可得kl=,最后将k+l=8,k2+l2=44代入后求解即可.
【解答】解:(1)①由题意得,
(m+n)2
=m2+2mn+n2
=(m2+n2)+2mn,
∴当mn=4,m2+n2=5时,
(m+n)2=5+2×4=5+8=13,
故答案为:13;
②∵(x+y)2=x2+2xy+y2,
∴xy===4,
故答案为:4;
③∵(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,
∴(a﹣b)2=(a+b)2﹣4ab=62﹣4×4=36﹣16=20,
故答案为:20;
(2)设AC=k,BC=l,可得k+l=8,k2+l2=44,
由完全平方公式(k+l)2=k2+2kl+l2,
可得kl=,
∴S△AFC=kl=×=5.
【点睛】此题考查了完全平方公式几何背景问题的解决能力,关键是能准确理解并运用完全平方公式和数形结合思想进行求解.
24.某商店分两次购进A,B型两种台灯进行销售,两次购进的数量及费用如下表所示,由于物价上涨,第二次购进A,B型两种台灯时,两种台灯每台进价分别上涨30%,20%.
购进的台数 购进所需要的费用(元)
A型 B型
第一次 10 20 3000
第二次 15 10 4500
(1)求第一次购进A,B型两种台灯每台进价分别是多少元?
(2)A,B型两种台灯销售单价不变,第一次购进的台灯全部售出后,获得的利润为2800元,第二次购进的台灯全部售出后,获得的利润为1800元.
①求A,B型两种台灯每台售价分别是多少元?
②若按照第二次购进A,B型两种台灯的价格再购进一次,将再次购进的台灯全部售出后,要想使获得的利润为1000元,求有哪几种购进方案?
【点拨】(1)设第一次购进A型台灯每台进价为x元,B型台灯每台进价为y元,由表中数据列出二元一次方程组,解方程组即可;
(2)①设A型台灯每台售价为m元,B型台灯每台售价为n元,由题意:第一次购进的台灯全部售出后,获得的利润为2800元,第二次购进的台灯全部售出后,获得的利润为1800元.列出二元一次方程组,解方程组即可;
②设购进A型台灯a台,B型台灯B台,由题意:想使获得的利润为1000元,列出二元一次方程,求出自然数解,即可解决问题.
【解答】解:(1)设第一次购进A型台灯每台进价为x元,B型台灯每台进价为y元,
由题意得:,
解得:,
答:第一次购进A型台灯每台进价为200元,B型台灯每台进价为50元;
(2)①设A型台灯每台售价为m元,B型台灯每台售价为n元,
由题意得:,
解得:,
答:A型台灯每台售价为340元,B型台灯每台售价为120元;
②第二次购进的A型台灯的价格为:200(1+30%)=260(元),B型台灯的价格为:50(1+20%)=60(元),
设购进A型台灯a台,B型台灯B台,
由题意得:(340﹣260)a+(120﹣60)b=1000,
整理得:4a+3b=50,
∵a、b为自然数,
∴或或或,
∴有4种购进方案:
①购进A型台灯2台,B型台灯14台;②购进A型台灯5台,B型台灯10台;③购进A型台灯8台,B型台灯6台;④购进A型台灯11台,B型台灯2台.
【点睛】本题考查二元一次方程组的应用以及二元一次方程的应用,找准等量关系,正确列出二元一次方程组或二元一次方程是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年第二学期七年级数学期中模拟试卷(1)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列是二元一次方程的是( )
A.3x﹣6y B.2x﹣3y=x2 C. D.3x﹣2y=0
2.华为麒麟9000处理器采用了5nm工艺制程,5nm=0.000000005m.把数0.000000005用科学记数法表示,记为( )
A.0.5×10﹣9 B.5×10﹣8 C.5×10﹣9 D.0.5×10﹣8
3.如图,直线a、b被直线c所截,则∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.如图,直线AB,CD被直线CE所截,AB∥CD,∠1=140°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
5.下列各运算中,计算正确的是( )
A.x3 (﹣x)2=x5 B.(﹣2x2)3=﹣6x6 C.a6÷a3=a2 D.(x﹣2)2=x2﹣4
6.若是方程2x+3y=﹣1的一个解,则6a+9b+4的值是( )
A.﹣2 B.1 C.3 D.7
7.若am=4,an=2,则a2m﹣n的值为( )
A.8 B.12 C.24 D.48
8.若是方程组的解,则a2﹣b2的值为( )
A. B. C.﹣16 D.16
9.盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )
A. B. C. D.
10.如图,图①所示的小长方形两条边的长分别为1,m(m>1),现将这样5个大小形状完全相同的小长方形不重叠地放入图②所示的大长方形中,图中未被覆盖部分用阴影表示,其面积分别为S1,S2.设面积为S1的长方形一条边为x.若无论x为何值,图中阴影部分S1﹣S2的值总保持不变,此时S1﹣S2的值为( )
A. B.2 C. D.3
二、填空题:本题共6小题,每小题3分,共18分。
11.计算:3x3 (﹣x)2= .
12.已知4x﹣y=3,用含x的代数式表示y,则y= .
13.如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加 (只填出一种即可)的条件.
14.如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于 .
15.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,阴影部分的面积为48,则平移距离为 .
16.若方程组的解是,则方程组的解是 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.因式分解:
(1)8abc﹣2bc2; (2)2x(x+y)﹣6(x+y).
18.计算:
(1)+(﹣1)2023+(π﹣3.14)0﹣|﹣3|; (2)(﹣2x2)3+x2 x4﹣(﹣3x3)2.
19.解方程组:
(1); (2).
20.先化简,再求值:[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷2x,其中x=3,y=﹣1.
21.如图,在所给4×4网格图(每个小格均为边长是1的正方形)中完成下列各题:
(1)△ABC的面积为 ;
(2)按下列要求作格点三角形(图形的顶点都在正方形格纸的格点上).
①在图1中,将△ABC平移,得到△A′B′C′,请画一个△A′B′C′与△ABC无重合部分.
②在图2中,线段AB与CD相交,产生∠α,请画一个△ABE,使得△ABE中的一个角等于∠α.
22.如图,在△ABC中,∠ACB=90°,点D,F在边AB上,过点D作DE∥BC交AC于点E,G为BC上一点,连接FG,且∠1+∠CGF=180°.
(1)求证:DC∥GF;
(2)若点E为AC的中点,且∠DCA=25°,求∠GFB的度数.
23.在“狼堡”密室里,灰太狼发现完全平方公式:(a±b)2=a2±2ab+b2经过适当的变形,可以解决很多数学问题,例如:若a+b=3,ab=1,求a2+b2的值.
解:∵a+b=3,ab=1,∴(a+b)2=9,2ab=2,
∴a2+b2+2ab=9,∴a2+b2=7.
根据上面灰太狼的解题思路与方法,请解决下列问题:
(1)①若mn=4,m2+n2=5,则(m+n)2= ;
②若x+y=6,x2+y2=28,则xy= ;
③若a+b=6,ab=4,则(a﹣b)2= ;
(2)如图,C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=44,求△AFC的面积.
24.某商店分两次购进A,B型两种台灯进行销售,两次购进的数量及费用如下表所示,由于物价上涨,第二次购进A,B型两种台灯时,两种台灯每台进价分别上涨30%,20%.
购进的台数 购进所需要的费用(元)
A型 B型
第一次 10 20 3000
第二次 15 10 4500
(1)求第一次购进A,B型两种台灯每台进价分别是多少元?
(2)A,B型两种台灯销售单价不变,第一次购进的台灯全部售出后,获得的利润为2800元,第二次购进的台灯全部售出后,获得的利润为1800元.
①求A,B型两种台灯每台售价分别是多少元?
②若按照第二次购进A,B型两种台灯的价格再购进一次,将再次购进的台灯全部售出后,要想使获得的利润为1000元,求有哪几种购进方案?
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列是二元一次方程的是( )
A.3x﹣6y B.2x﹣3y=x2 C. D.3x﹣2y=0
【点拨】利用二元一次方程的定义,逐一分析四个选项中的方程,即可得出结论.
【解答】解:A.方程3x﹣6不是一元一次方程,选项A不符合题意;
B.方程2x﹣3y=x2是二元二次方程,选项B不符合题意;
C.方程2x﹣=1是分式方程,选项C不符合题意;
D.方程3x﹣2y=0是二元一次方程,选项D符合题意.
故选:D.
【点睛】本题考查了二元一次方程的定义,牢记“含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程”是解题的关键.
2.华为麒麟9000处理器采用了5nm工艺制程,5nm=0.000000005m.把数0.000000005用科学记数法表示,记为( )
A.0.5×10﹣9 B.5×10﹣8 C.5×10﹣9 D.0.5×10﹣8
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:0.000000005=5×10﹣9.
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.如图,直线a、b被直线c所截,则∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【点拨】根据内错角的定义求解.
【解答】解:∠1的内错角是∠3.
故选:B.
【点睛】本题主要考查了同位角、内错角、同旁内角,对顶角、邻补角,关键掌握两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
4.如图,直线AB,CD被直线CE所截,AB∥CD,∠1=140°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
【点拨】先根据补角的定义得出∠AEC的度数,再由平行线的性质即可得出结论.
【解答】解:∵∠1=140°,
∴∠AEC=180°﹣140°=40°,
∵AB∥CD,
∴∠C=∠AEC=40°.
故选:B.
【点睛】本题考查的是平行线的性质,熟知两直线平行,内错角相等是解题的关键.
5.下列各运算中,计算正确的是( )
A.x3 (﹣x)2=x5 B.(﹣2x2)3=﹣6x6 C.a6÷a3=a2 D.(x﹣2)2=x2﹣4
【点拨】利用完全平方公式,同底数幂的乘除法运算法则以及积的乘方分别分析得出即可.
【解答】解:A、x3 (﹣x)2=x5,故正确,符合题意;
B、(﹣2x2)3=﹣8x6,故故错误,不符合题意;
C、x6÷x3=x3,故错误,不符合题意;
D、(x﹣2)2=x2﹣4x+4,故错误,不符合题意.
故选:A.
【点睛】此题主要考查了完全平方公式,同底数幂的乘除法,幂的乘方与积的乘方,掌握相应的运算法则是解题关键.
6.若是方程2x+3y=﹣1的一个解,则6a+9b+4的值是( )
A.﹣2 B.1 C.3 D.7
【点拨】将x=a,y=b代入方程2x+3y=﹣1,得,2a+3b=﹣1,可得6a+9b=﹣3,即得6a+9b+4的值.
【解答】解:将x=a,y=b代入方程2x+3y=﹣1,
得,2a+3b=﹣1,
∴6a+9b=﹣3,
∴6a+9b+4=1,
故选:B.
【点睛】本题考查了二元一次方程的解,将方程的一个解x=a,y=b代入方程求得2a+3b的值是本题的关键.
7.若am=4,an=2,则a2m﹣n的值为( )
A.8 B.12 C.24 D.48
【点拨】利用幂的乘方与积的乘方的法则,同底数幂的除法法则进行计算,即可得出答案.
【解答】解:∵am=4,an=2,
∴a2m﹣n
=a2m÷an
=(am)2÷an
=42÷2
=16÷2
=8,
故选:A.
【点睛】本题考查了幂的乘方与积的乘方,同底数幂的除法,掌握幂的乘方与积的乘方的法则,同底数幂的除法法则是解决问题的关键.
8.若是方程组的解,则a2﹣b2的值为( )
A. B. C.﹣16 D.16
【点拨】把代入原方程组得,解出a+b与a﹣b,再进一步即可求出答案.
【解答】解:把代入原方程组
得,
∴两个方程相加得:3a+3b=8即,
两个方程相减得:a﹣b=6,
∴,
故选:D.
【点睛】本题考查了二元一次方程和利用平方差公式分解因式,学生们熟练掌握二元一次方程的计算和平方差公式的计算即可.
9.盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )
A. B. C. D.
【点拨】设用x米布料做玩偶A,用y米布料做玩偶B,根据等量关系式:玩偶A的个数×2=玩偶B的个数,玩偶A用的布料+玩偶B用的布料=136米,列出方程组即可.
【解答】解:设用x米布料做玩偶A,用y米布料做玩偶B,由题意可得,
,故C正确.
故选:C.
【点睛】本题主要考查了二元一次方程组的应用,根据题意找出题目中的等量关系式,是解题的关键.
10.如图,图①所示的小长方形两条边的长分别为1,m(m>1),现将这样5个大小形状完全相同的小长方形不重叠地放入图②所示的大长方形中,图中未被覆盖部分用阴影表示,其面积分别为S1,S2.设面积为S1的长方形一条边为x.若无论x为何值,图中阴影部分S1﹣S2的值总保持不变,此时S1﹣S2的值为( )
A. B.2 C. D.3
【点拨】由题意可得图②中AB=m+3,BC=x+2,由此表示出阴影部分S1﹣S2的面积,然后令含x的项的系数之和为0,列方程求得m的值,从而求解.
【解答】解:由题意可得:AB=m+3,BC=x+2,
∴S1﹣S2=xm﹣3(x+2﹣m)
=xm﹣3x﹣6+3m
=(m﹣3)x﹣6+3m,
又∵阴影部分S1﹣S2的值总保持不变,
∴m﹣3=0,
解得:m=3,
∴S1﹣S2=﹣6+3×3=3,
故选:D.
【点睛】本题考查整式加减运算的应用,准确识图,用含x和m的式子表示出S1﹣S2是解题关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.计算:3x3 (﹣x)2= 3x5 .
【点拨】先根据积的乘方法则计算乘方,再根据单项式乘单项式法则计算乘法即可.
【解答】解:原式=3x3 x2
=3x5,
故答案为:3x5.
【点睛】本题主要考查了整式的混合运算,解题关键是熟练掌握积的乘方法则、同底数幂相乘法则和单项式乘单项式法则.
12.已知4x﹣y=3,用含x的代数式表示y,则y= 4x﹣3 .
【点拨】根据等式的性质解答即可.
【解答】解:4x﹣y=3,
等式两边同时加上y,得4x﹣y+y=3+y,即4x=3+y,
等式两边同时减去3,得4x﹣3=3+y﹣3,
∴y=4x﹣3,
故答案为:y=4x﹣3.
【点睛】本题考查了等式的性质,二元一次方程,掌握等式的性质是解题的关键.
13.如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加 ∠ACD=90°(答案不唯一). (只填出一种即可)的条件.
【点拨】由平行线的判定,即可得到答案.
【解答】解:∵AB⊥AC,
∴∠BAC=90°,
若∠ACD=90°,则∠BAC=∠ACD,
∴AB∥CD,
∴要使AB∥CD,可添加∠ACD=90°(答案不唯一).
故答案为:∠ACD=90°(答案不唯一).
【点睛】本题考查平行线的判定,关键是掌握平行线的判定方法.
14.如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于 55° .
【点拨】利用平行线的性质及角的和差即可求得答案.
【解答】解:如图,设直角三角形的顶点分别为A,B,C,其斜边交直线b于点D,
∵直线a∥b∥c,
∴∠1=∠ACD,∠2=∠BCD,
∵∠ACD+∠BCD=90°,
∴∠1+∠2=90°,
∵∠1=35°,
∴∠2=90°﹣35°=55°,
故答案为:55°.
【点睛】本题考查平行线性质及角的计算,结合已知条件求得∠1+∠2=90°是解题的关键.
15.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,阴影部分的面积为48,则平移距离为 6 .
【点拨】根据平移的性质可知:AB=DE,由此可求出EH的长.由S阴影DHCF=S梯形ABEH结合梯形的面积公式即可求出BE.
【解答】解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DE=AB=10,DE∥AB,S△ABC=S△DEF,
∴EH=10﹣4=6,S阴影DHCF=S梯形ABEH=48,
∴(EH+AB)BE=48,
∴(6+10)BE=48,
∴BE=6,即平移的距离为6.
故答案为:6.
【点睛】本题考查了平移的性质,对应点连线的长度等于平移距离,平移变化只改变图形的位置不改变图形的形状,熟记各性质并判断出阴影部分面积等于梯形ABEH的面积是解题的关键.
16.若方程组的解是,则方程组的解是 .
【点拨】仿照已知方程组的解确定出所求方程组的解即可.
【解答】解:∵方程组的解是,
∴方程组的解是,即.
故答案为:.
【点睛】此题考查了二次一次方程组的解,以及解二元一次方程组,利用了类比的思想,熟练掌握运算法则是解本题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.因式分解:
(1)8abc﹣2bc2; (2)2x(x+y)﹣6(x+y).
【点拨】(1)提公因式法因式分解;
(2)提公因式法因式分解.
【解答】解:(1)8abc﹣2bc2=2bc(4a﹣c);
(2)2x(x+y)﹣6(x+y)=2(x+y)(x﹣3).
【点睛】本题考查了因式分解﹣提公因式法,解题的关键是掌握因式分解的方法.
18.计算:
(1)+(﹣1)2023+(π﹣3.14)0﹣|﹣3|;
(2)(﹣2x2)3+x2 x4﹣(﹣3x3)2.
【点拨】(1)先化简各式,然后再进行计算即可解答;
(2)先算乘方,再算乘法,后算加减,即可解答.
【解答】解:(1)+(﹣1)2023+(π﹣3.14)0﹣|﹣3|
=4+(﹣1)+1﹣3
=3+1﹣3
=1;
(2)(﹣2x2)3+x2 x4﹣(﹣3x3)2
=﹣8x6+x6﹣9x6
=﹣16x6.
【点睛】本题考查了整式的混合运算,实数的运算,幂的乘方与积的乘方,同底数幂的乘法,零指数幂,负整数指数幂,准确熟练地进行计算是解题的关键.
19.解方程组:
(1); (2).
【点拨】(1)利用加减消元法解方程组即可;
(2)将原方程组整理后利用加减消元法解方程组即可.
【解答】解:(1),
①﹣②×3得:8y=0,
解得:y=0,
将y=0代入①得:3x=6,
解得:x=2,
故原方程组的解为;
(2)原方程组整理得,
①×3﹣②得:25y=150,
解得:y=6,
将y=6代入②得:3x﹣6=12,
解得:x=6,
故原方程组的解为.
【点睛】本题考查解二元一次方程组,熟练掌握解方程组的方法是解题的关键.
20.先化简,再求值:[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷2x,其中x=3,y=﹣1.
【点拨】先利用完全平方公式、平方差公式、多项式除以单项式法则化简整式,再代入求值.
【解答】解:[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷2x
=[9x2﹣6xy+y2﹣(x2﹣y2)﹣2y2]÷2x
=(9x2﹣6xy+y2﹣x2+y2﹣2y2)÷2x
=(8x2﹣6xy)÷2x
=4x﹣3y.
当x=3,y=﹣1时,
原式=4×3﹣3×(﹣1)
=12+3
=15.
【点睛】本题考查了整式的化简求值,掌握整式的运算法则、乘法公式等知识点是解决本题的关键.
21.如图,在所给4×4网格图(每个小格均为边长是1的正方形)中完成下列各题:
(1)△ABC的面积为 2.5 ;
(2)按下列要求作格点三角形(图形的顶点都在正方形格纸的格点上).
①在图1中,将△ABC平移,得到△A′B′C′,请画一个△A′B′C′与△ABC无重合部分.
②在图2中,线段AB与CD相交,产生∠α,请画一个△ABE,使得△ABE中的一个角等于∠α.
【点拨】(1)利用割补法求解即可;
(2)①把△ABC向右平移2个单位即可;
②把CD向右平移2个单位,C点与A点重合,则D点的对应点为E点.
【解答】解:(1),
故答案为:2.5;
(2)①如图1,△A′B′C′为所作;
②如图2,△ABE为所作.
∵AE∥CD,
∴∠A=∠α,
∴△ABE即为所求.
【点睛】本题考查了平移作图,割补法求面积,解答本题的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
22.如图,在△ABC中,∠ACB=90°,点D,F在边AB上,过点D作DE∥BC交AC于点E,G为BC上一点,连接FG,且∠1+∠CGF=180°.
(1)求证:DC∥GF;
(2)若点E为AC的中点,且∠DCA=25°,求∠GFB的度数.
【点拨】(1)先由DE∥BC得∠1=∠BCD,进而可得∠BCD+∠CGF=180°,然后根据平行线的判定可得出结论;
(2)先证DE⊥AC,进而得DE是线段AC的垂直平分线,则DC=DA,由此得∠A=∠DCA=25°,从而可求出∠ADE=65°,∠1=65°,进而得∠ADC=∠ADE+∠1=130°,由此可得∠CDB=180°﹣∠ADC=50°,然后在由(1)的结论可知DC∥GF,最后根据平行线的性质可得∠GFB的度数.
【解答】(1)证明:∵DE∥BC,
∴∠1=∠BCD,
又∵∠1+∠CGF=180°,
∴∠BCD+∠CGF=180°,
∴DC∥GF;
(2)解:∵∠ACB=90°,DE∥BC,
∴∠DEA=∠ACB=90°,
即DE⊥AC,
又∵点E为AC的中点,
∴DE是线段AC的垂直平分线,
∴DC=DA,
∴∠A=∠DCA=25°,
∴∠ADE=90°﹣∠A=65°,∠1=90°﹣∠DCA=65°,
∴∠ADC=∠ADE+∠1=130°,
∴∠CDB=180°﹣∠ADC=50°,
由(1)可知:DC∥GF,
∴∠GFB=∠CDB=50°.
【点睛】此题主要考查了平行线的判定和性质,线段垂直平分线的性质,等腰三角形的性质,直角三角形的性质等,熟练掌握平行线的判定和性质,线段垂直平分线的性质,理解等腰三角形的两个底角相等,直角三角形的两个锐角互余是解决问题的关键.
23.在“狼堡”密室里,灰太狼发现完全平方公式:(a±b)2=a2±2ab+b2经过适当的变形,可以解决很多数学问题,例如:若a+b=3,ab=1,求a2+b2的值.
解:∵a+b=3,ab=1,∴(a+b)2=9,2ab=2,
∴a2+b2+2ab=9,∴a2+b2=7.
根据上面灰太狼的解题思路与方法,请解决下列问题:
(1)①若mn=4,m2+n2=5,则(m+n)2= 13 ;
②若x+y=6,x2+y2=28,则xy= 4 ;
③若a+b=6,ab=4,则(a﹣b)2= 20 ;
(2)如图,C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=44,求△AFC的面积.
【点拨】(1)①运用完全平方公式,将mn=4,m2+n2=5代入(m+n)2=m2+2mn+n2进行求解;
②先将(x+y)2=x2+2xy+y2变形为xy=,再将x+y=6,x2+y2=28代入求解;
③先由(a±b)2=a2±2ab+b2可得(a﹣b)2=(a+b)2﹣4ab,再将a+b=6,ab=4代入求解;
(2)设AC=k,BC=l,可得k+l=8,k2+l2=44,再由完全平方公式可得kl=,最后将k+l=8,k2+l2=44代入后求解即可.
【解答】解:(1)①由题意得,
(m+n)2
=m2+2mn+n2
=(m2+n2)+2mn,
∴当mn=4,m2+n2=5时,
(m+n)2=5+2×4=5+8=13,
故答案为:13;
②∵(x+y)2=x2+2xy+y2,
∴xy===4,
故答案为:4;
③∵(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,
∴(a﹣b)2=(a+b)2﹣4ab=62﹣4×4=36﹣16=20,
故答案为:20;
(2)设AC=k,BC=l,可得k+l=8,k2+l2=44,
由完全平方公式(k+l)2=k2+2kl+l2,
可得kl=,
∴S△AFC=kl=×=5.
【点睛】此题考查了完全平方公式几何背景问题的解决能力,关键是能准确理解并运用完全平方公式和数形结合思想进行求解.
24.某商店分两次购进A,B型两种台灯进行销售,两次购进的数量及费用如下表所示,由于物价上涨,第二次购进A,B型两种台灯时,两种台灯每台进价分别上涨30%,20%.
购进的台数 购进所需要的费用(元)
A型 B型
第一次 10 20 3000
第二次 15 10 4500
(1)求第一次购进A,B型两种台灯每台进价分别是多少元?
(2)A,B型两种台灯销售单价不变,第一次购进的台灯全部售出后,获得的利润为2800元,第二次购进的台灯全部售出后,获得的利润为1800元.
①求A,B型两种台灯每台售价分别是多少元?
②若按照第二次购进A,B型两种台灯的价格再购进一次,将再次购进的台灯全部售出后,要想使获得的利润为1000元,求有哪几种购进方案?
【点拨】(1)设第一次购进A型台灯每台进价为x元,B型台灯每台进价为y元,由表中数据列出二元一次方程组,解方程组即可;
(2)①设A型台灯每台售价为m元,B型台灯每台售价为n元,由题意:第一次购进的台灯全部售出后,获得的利润为2800元,第二次购进的台灯全部售出后,获得的利润为1800元.列出二元一次方程组,解方程组即可;
②设购进A型台灯a台,B型台灯B台,由题意:想使获得的利润为1000元,列出二元一次方程,求出自然数解,即可解决问题.
【解答】解:(1)设第一次购进A型台灯每台进价为x元,B型台灯每台进价为y元,
由题意得:,
解得:,
答:第一次购进A型台灯每台进价为200元,B型台灯每台进价为50元;
(2)①设A型台灯每台售价为m元,B型台灯每台售价为n元,
由题意得:,
解得:,
答:A型台灯每台售价为340元,B型台灯每台售价为120元;
②第二次购进的A型台灯的价格为:200(1+30%)=260(元),B型台灯的价格为:50(1+20%)=60(元),
设购进A型台灯a台,B型台灯B台,
由题意得:(340﹣260)a+(120﹣60)b=1000,
整理得:4a+3b=50,
∵a、b为自然数,
∴或或或,
∴有4种购进方案:
①购进A型台灯2台,B型台灯14台;②购进A型台灯5台,B型台灯10台;③购进A型台灯8台,B型台灯6台;④购进A型台灯11台,B型台灯2台.
【点睛】本题考查二元一次方程组的应用以及二元一次方程的应用,找准等量关系,正确列出二元一次方程组或二元一次方程是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
