【专项培优】沪科版数学(2024)七年级下册第十章相交线平行线与平移(含答案)
文档属性
| 名称 | 【专项培优】沪科版数学(2024)七年级下册第十章相交线平行线与平移(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 520.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 08:58:01 | ||
图片预览



文档简介
)
中小学教育资源及组卷应用平台
【专项培优】沪科版数学(2024)七年级下册第十章相交线平行线与平移
一、单选题
1.(2019七下·鹿邑期末)如图,已知 ,则 ( )
A. B. C. D.
2.(2023七下·霸州期中)如图,以每秒的速度沿着射线向右平移,平移2秒后所得图形是,连接,如果,那么的长是( )
A. B. C. D.
3.下列生活实例:①“车让人”路口的斑马线;②天上的彩虹; ③长方形门框的上 下边;④百米直线跑道;⑤高速铁路的平直轨道.其中给我们以“平行线”的印象的实例有( )
A.1个 B.2个 C.3个 D.4个
4.(2021七下·襄汾期末)如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中,不正确的是( )
A. B.
C. D.
5.(2023七下·南宁期中)下图是德胜中学的校徽,将它通过平移可得到的图形是( )
A. B. C. D.
6.(2024七下·鄞州期中)如图,∠1=80°,∠2=80°,∠3=84°,则∠4=( )
A.84° B.94° C.86° D.96°
7.(2022七下·馆陶期末)如图,正方形网格中,能由平移得到的线段是( )
A. B. C. D.
8.如图,下列说法错误的是( )
A.∠1与∠3是同位角 B.∠A与∠C是同旁内角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
9.(2022七下·老边期中)如图,如果AB∥CD,那么下面说法错误的是( )
A.∠3=∠7 B.∠2=∠6
C.∠3+∠4+∠5+∠6=180° D.∠4=∠8
10.(2023七下·黄岩期末)如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A.或或 B.或或
C.或或 D.或或
二、填空题
11.(2024七下·涟水期中)如图,写出能判定的一个条件 (写出一个即可).
12.(2024七下·江门期中)如图,已知长方形ABCD的长为a,宽为b,若将长方形ABCD向右平移a,再向下平移b,得到长方形,则阴影部分的面积为 (用含a、b的代数式表示).
13.(2024七下·醴陵期末)如图,中,,将边向右平移4个单位得到,则四边形的周长为 .
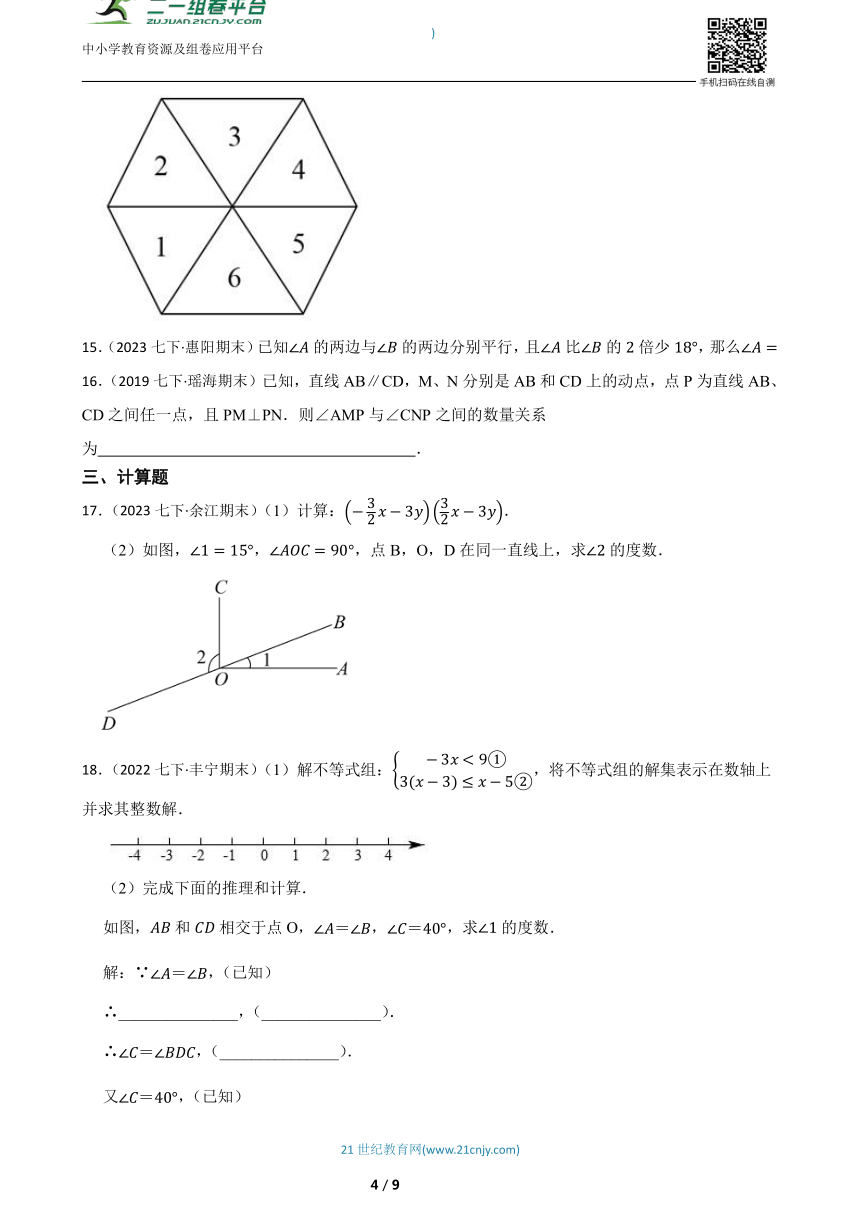
14.(2020七下·澄迈期末)下图是由六个大小一样的等边三角形拼成的图形,能由标号为1的三角形平移而得到的是 号三角形(填写序号即可).
15.(2023七下·惠阳期末)已知的两边与的两边分别平行,且比的倍少,那么
16.(2019七下·瑶海期末)已知,直线AB∥CD,M、N分别是AB和CD上的动点,点P为直线AB、CD之间任一点,且PM⊥PN.则∠AMP与∠CNP之间的数量关系为 .
三、计算题
17.(2023七下·余江期末)(1)计算:.
(2)如图,,,点B,O,D在同一直线上,求的度数.
18.(2022七下·丰宁期末)(1)解不等式组:,将不等式组的解集表示在数轴上并求其整数解.
(2)完成下面的推理和计算.
如图,和相交于点O,,,求的度数.
解:∵,(已知)
∴_______________,(_______________).
∴,(_______________).
又,(已知)
∴_______________(等量代换)
∴_______________=_______________.
19.(2021七下·大兴期中)在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F.
(1)如图,当点E在线段CD上时,求证:∠DEF=∠DCB.
(2)若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .
四、解答题
20.(2023七下·惠城月考)如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
21.(2023七下·南岸期中)阅读下列推理过程,在括号中填写理由.
如图,已知,,垂足分别为、,.试说明:.
解:∵,(已知)
∴( )
∴EF∥AD( )
∴ ( )
又∵(已知)
∴ ( )
∴ ∥ ( )
∴( )
22.(2023七下·韩城期末)如图,为上一点,为上一点,,.与平行吗?说明理由.
23.(2024七下·江夏月考)江夏文旅局计划“五·一”期间在中央公园举行大型灯光秀活动,沿湖两岸设置两座可以旋转的射灯,如图1,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射,若灯A转动的速度是2度/秒,灯B转动的速度是1度/秒,假定湖两岸是平行的,即PQ//MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=
(2)若灯B射线先转动30s,灯A射线才开始转动,在灯B射线到达BQ之前,灯A转动几秒,两灯的光束互相平行
(3)如图2,若两灯同时转动,在灯A射线到达AN之前,假设射出的光束交点C,过点C作∠ACD交PQ于点D,且∠ACD=1200,请探究:在转动过程中,∠BAC与∠BCD之间的数量关系是否发生变化 若不变,请求出其数量关系;若改变,请说明理由 .
答案解析部分
1.【答案】C
【知识点】平行线的判定与性质
2.【答案】B
【知识点】平移的性质
3.【答案】D
【知识点】平行线的定义与现象
4.【答案】A
【知识点】平移的性质
5.【答案】C
【知识点】生活中的平移现象
6.【答案】D
【知识点】平行线的判定与性质
7.【答案】B
【知识点】图形的平移
8.【答案】A
【知识点】同位角的概念;内错角的概念;同旁内角的概念
9.【答案】D
【知识点】平行线的性质
10.【答案】C
【知识点】平行线的性质
11.【答案】(答案不唯一)
【知识点】平行线的判定
12.【答案】1.2ab
【知识点】整式的加减运算;平移的性质;用代数式表示几何图形的数量关系
13.【答案】
【知识点】平移的性质
14.【答案】3和5
【知识点】平移的性质
15.【答案】或
【知识点】平行线的性质
16.【答案】∠AMP+∠CNP=90°或∠AMP+∠CNP=270°
【知识点】平行线的判定与性质
17.【答案】(1);(2)
【知识点】平方差公式及应用;邻补角
18.【答案】(1);整数解为,,0,1,2;(2);内错角相等,两直线平行;两直线平行,内错角相等;;;140
【知识点】解一元一次不等式组;一元一次不等式组的特殊解;平行线的判定与性质
19.【答案】(1)证明:∵AB∥DC,
∴∠B+∠BCD=180°,
∵∠BAD=∠BCD,
∴∠B+∠BAD=180°,
∴AD∥BC,
∵EF∥AD,
∴EF∥BC,
∴∠DEF=∠DCB.
(2)∠DEF+∠DCB=180°
【知识点】平行线的判定与性质
20.【答案】(1)
(2)
【知识点】平行线的性质;平行线的判定与性质
21.【答案】垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;∠3;同角的补角相等; AB;DG;内错角相等,两直线平行;两直线平行,同位角相等
【知识点】余角、补角及其性质;垂线的概念;平行线的判定与性质
22.【答案】解:平行
理由:∵,,
∴,
∴,
∴
∵.
∴,
∴.
【知识点】平行线的判定与性质
23.【答案】(1)60°
(2)解:设灯转动时间为秒两灯的光束互相平行.
①当时,
解得,
②当时,
解得,
综上:或
(3)解:和关系不会变化
理由:设灯射线转动时间为秒,
和关系不会变化
【知识点】平行线的判定与性质;一元一次方程的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 9
中小学教育资源及组卷应用平台
【专项培优】沪科版数学(2024)七年级下册第十章相交线平行线与平移
一、单选题
1.(2019七下·鹿邑期末)如图,已知 ,则 ( )
A. B. C. D.
2.(2023七下·霸州期中)如图,以每秒的速度沿着射线向右平移,平移2秒后所得图形是,连接,如果,那么的长是( )
A. B. C. D.
3.下列生活实例:①“车让人”路口的斑马线;②天上的彩虹; ③长方形门框的上 下边;④百米直线跑道;⑤高速铁路的平直轨道.其中给我们以“平行线”的印象的实例有( )
A.1个 B.2个 C.3个 D.4个
4.(2021七下·襄汾期末)如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中,不正确的是( )
A. B.
C. D.
5.(2023七下·南宁期中)下图是德胜中学的校徽,将它通过平移可得到的图形是( )
A. B. C. D.
6.(2024七下·鄞州期中)如图,∠1=80°,∠2=80°,∠3=84°,则∠4=( )
A.84° B.94° C.86° D.96°
7.(2022七下·馆陶期末)如图,正方形网格中,能由平移得到的线段是( )
A. B. C. D.
8.如图,下列说法错误的是( )
A.∠1与∠3是同位角 B.∠A与∠C是同旁内角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
9.(2022七下·老边期中)如图,如果AB∥CD,那么下面说法错误的是( )
A.∠3=∠7 B.∠2=∠6
C.∠3+∠4+∠5+∠6=180° D.∠4=∠8
10.(2023七下·黄岩期末)如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A.或或 B.或或
C.或或 D.或或
二、填空题
11.(2024七下·涟水期中)如图,写出能判定的一个条件 (写出一个即可).
12.(2024七下·江门期中)如图,已知长方形ABCD的长为a,宽为b,若将长方形ABCD向右平移a,再向下平移b,得到长方形,则阴影部分的面积为 (用含a、b的代数式表示).
13.(2024七下·醴陵期末)如图,中,,将边向右平移4个单位得到,则四边形的周长为 .
14.(2020七下·澄迈期末)下图是由六个大小一样的等边三角形拼成的图形,能由标号为1的三角形平移而得到的是 号三角形(填写序号即可).
15.(2023七下·惠阳期末)已知的两边与的两边分别平行,且比的倍少,那么
16.(2019七下·瑶海期末)已知,直线AB∥CD,M、N分别是AB和CD上的动点,点P为直线AB、CD之间任一点,且PM⊥PN.则∠AMP与∠CNP之间的数量关系为 .
三、计算题
17.(2023七下·余江期末)(1)计算:.
(2)如图,,,点B,O,D在同一直线上,求的度数.
18.(2022七下·丰宁期末)(1)解不等式组:,将不等式组的解集表示在数轴上并求其整数解.
(2)完成下面的推理和计算.
如图,和相交于点O,,,求的度数.
解:∵,(已知)
∴_______________,(_______________).
∴,(_______________).
又,(已知)
∴_______________(等量代换)
∴_______________=_______________.
19.(2021七下·大兴期中)在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F.
(1)如图,当点E在线段CD上时,求证:∠DEF=∠DCB.
(2)若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .
四、解答题
20.(2023七下·惠城月考)如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
21.(2023七下·南岸期中)阅读下列推理过程,在括号中填写理由.
如图,已知,,垂足分别为、,.试说明:.
解:∵,(已知)
∴( )
∴EF∥AD( )
∴ ( )
又∵(已知)
∴ ( )
∴ ∥ ( )
∴( )
22.(2023七下·韩城期末)如图,为上一点,为上一点,,.与平行吗?说明理由.
23.(2024七下·江夏月考)江夏文旅局计划“五·一”期间在中央公园举行大型灯光秀活动,沿湖两岸设置两座可以旋转的射灯,如图1,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射,若灯A转动的速度是2度/秒,灯B转动的速度是1度/秒,假定湖两岸是平行的,即PQ//MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=
(2)若灯B射线先转动30s,灯A射线才开始转动,在灯B射线到达BQ之前,灯A转动几秒,两灯的光束互相平行
(3)如图2,若两灯同时转动,在灯A射线到达AN之前,假设射出的光束交点C,过点C作∠ACD交PQ于点D,且∠ACD=1200,请探究:在转动过程中,∠BAC与∠BCD之间的数量关系是否发生变化 若不变,请求出其数量关系;若改变,请说明理由 .
答案解析部分
1.【答案】C
【知识点】平行线的判定与性质
2.【答案】B
【知识点】平移的性质
3.【答案】D
【知识点】平行线的定义与现象
4.【答案】A
【知识点】平移的性质
5.【答案】C
【知识点】生活中的平移现象
6.【答案】D
【知识点】平行线的判定与性质
7.【答案】B
【知识点】图形的平移
8.【答案】A
【知识点】同位角的概念;内错角的概念;同旁内角的概念
9.【答案】D
【知识点】平行线的性质
10.【答案】C
【知识点】平行线的性质
11.【答案】(答案不唯一)
【知识点】平行线的判定
12.【答案】1.2ab
【知识点】整式的加减运算;平移的性质;用代数式表示几何图形的数量关系
13.【答案】
【知识点】平移的性质
14.【答案】3和5
【知识点】平移的性质
15.【答案】或
【知识点】平行线的性质
16.【答案】∠AMP+∠CNP=90°或∠AMP+∠CNP=270°
【知识点】平行线的判定与性质
17.【答案】(1);(2)
【知识点】平方差公式及应用;邻补角
18.【答案】(1);整数解为,,0,1,2;(2);内错角相等,两直线平行;两直线平行,内错角相等;;;140
【知识点】解一元一次不等式组;一元一次不等式组的特殊解;平行线的判定与性质
19.【答案】(1)证明:∵AB∥DC,
∴∠B+∠BCD=180°,
∵∠BAD=∠BCD,
∴∠B+∠BAD=180°,
∴AD∥BC,
∵EF∥AD,
∴EF∥BC,
∴∠DEF=∠DCB.
(2)∠DEF+∠DCB=180°
【知识点】平行线的判定与性质
20.【答案】(1)
(2)
【知识点】平行线的性质;平行线的判定与性质
21.【答案】垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;∠3;同角的补角相等; AB;DG;内错角相等,两直线平行;两直线平行,同位角相等
【知识点】余角、补角及其性质;垂线的概念;平行线的判定与性质
22.【答案】解:平行
理由:∵,,
∴,
∴,
∴
∵.
∴,
∴.
【知识点】平行线的判定与性质
23.【答案】(1)60°
(2)解:设灯转动时间为秒两灯的光束互相平行.
①当时,
解得,
②当时,
解得,
综上:或
(3)解:和关系不会变化
理由:设灯射线转动时间为秒,
和关系不会变化
【知识点】平行线的判定与性质;一元一次方程的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 9
