2025年中考数学压轴题专练:旋转综合题(面积问题)(含解析)
文档属性
| 名称 | 2025年中考数学压轴题专练:旋转综合题(面积问题)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 07:28:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2025年中考数学压轴题专练:旋转综合题(面积问题)
1.如图1,在中,,,点、分别在边、上,,连接,点、、分别为、、的中点.
(1)观察猜想:图1中,线段与的数量关系是 ,位置关系是 ;
(2)探究证明:把绕点A逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点A在平面内自由旋转,若,,直接写出面积的最大值.
2.已知正方形边长为1,对角线相交于点O,过点O作射线,分别交于点E,F,且.
(1)如图1,当时,求证:四边形是正方形;
(2)如图2,将射线绕着点O进行旋转.
①在旋转过程中,判断线段与的数量关系,并给出证明;
②四边形的面积为 ;
(3)如图3,在四边形中,,连接.若,请直接写出四边形的面积.
3.如图1,在等腰中,,点D、E分别在边、上,,连接,点M、P、N分别为、、的中点.
(1)观察猜想:
图1中,线段与的数量关系是______,位置关系是______;
(2)探究证明:
把绕点A逆时针方向旋转到图2的位置,连接,,判断的形状,并说明理由;
(3)拓展延伸:
把绕点A在平面内自由旋转,若,,求面积的最大值.
4.在中,,连接,已知,点E在线段上,将线段绕点D顺时针旋转 为线段.
(1)如图1,线段与线段的交点和点E重合,连接,求线段的长度;
(2)如图2,点G为延长线上一点,使得,连接交于点H,求证:;
(3)如图3,在(2)的条件下,平面内一点P,当最小时,求的面积.
5.【问题初探】(1)如图1,为等边三角形内一点,满足,,,试求的大小.李明同学的思路是:将绕点逆时针旋转60°,点的对应点为,画出旋转后的图形,再连接.将求分成求和的和即可.请你按照李明同学给出的旋转的思路,求的大小;
【问题解决】(2)如图2,在正方形中,,分别为,边上的点,满足,若,,求的面积;
【问题拓展】(3)如图3,在四边形,,,,求的长.
6.在和中,,,,若,.
(1)如图1,当点在线段上时,连接,求;
(2)如图2.将图1中绕着点旋转,使点在的内部,连接,.线段,相交于点,且,此时_______;
(3)如图3,在绕着点旋转过程中,当点落在线段上时,过点作交直线于点,直接写出的面积.
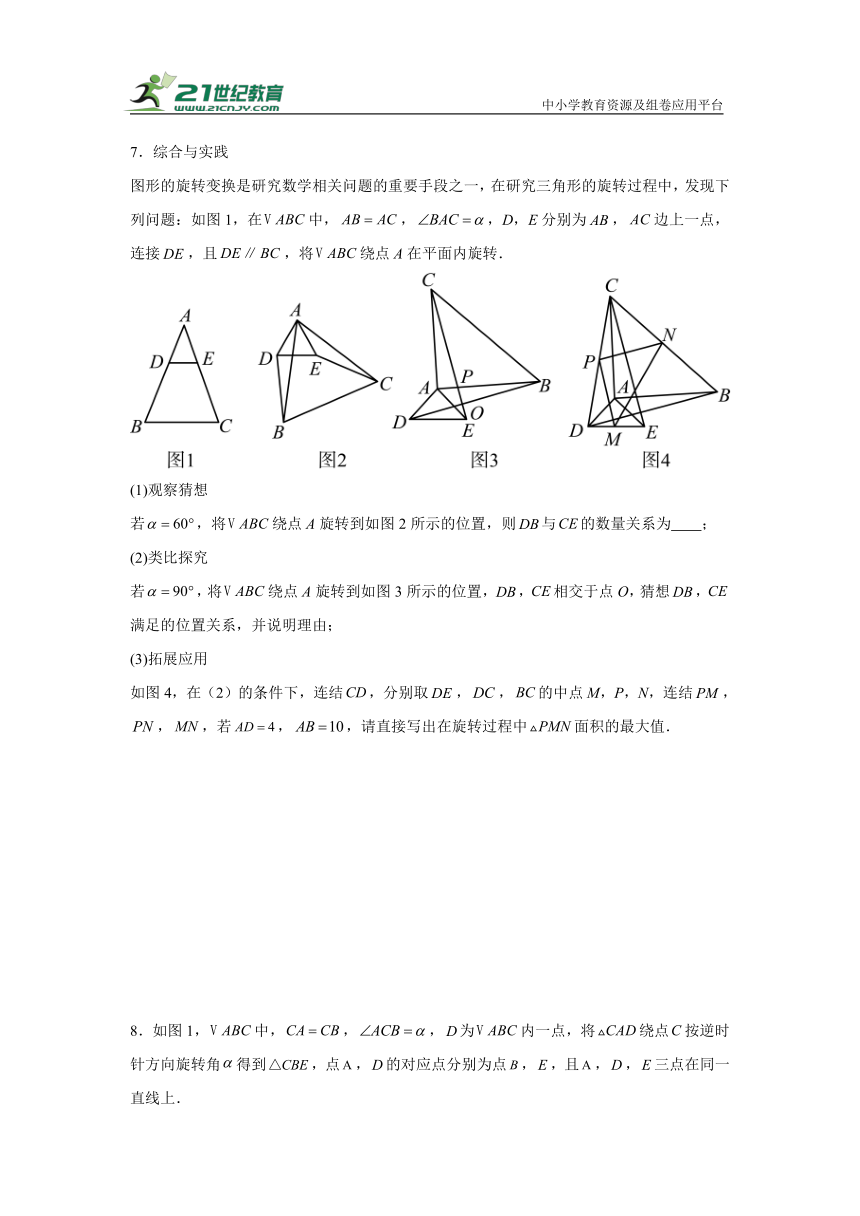
7.综合与实践
图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图1,在中,,,D,E分别为,边上一点,连接,且,将绕点A在平面内旋转.
(1)观察猜想
若,将绕点A旋转到如图2所示的位置,则与的数量关系为 ;
(2)类比探究
若,将绕点A旋转到如图3所示的位置,,相交于点O,猜想,满足的位置关系,并说明理由;
(3)拓展应用
如图4,在(2)的条件下,连结,分别取,,的中点M,P,N,连结,,,若,,请直接写出在旋转过程中面积的最大值.
8.如图1,中,,,为内一点,将绕点按逆时针方向旋转角得到,点,的对应点分别为点,,且,,三点在同一直线上.
(1)填空: ;(用含α的代数式表示)
(2)如图2,若,请补全图形,再过点作于点,然后探究线段,,之间的数量关系,并证明你的结论;
(3)如图3,若,,求四边形面积的最大值.
9.如图1,矩形中,,,将矩形绕着点B顺时针旋转,得到矩形.
(1)当点E落在上时,则线段的长度等于 ;
(2)如图2,当点E落在上时,求的面积;
(3)如图3,连接、、、,判断线段与的位置关系且说明理由;
(4)在旋转过程中,请直接写出的最大值.
10.已知和都是等腰三角形,.
(1)如图①,当点D在外部,点E在内部时,求证:.
(2)如图②,和都是等腰直角三角形,,点C,D,E在同一直线上,为中边上的高.求的度数;判断线段之间的数量关系,并说明理由.
(3)如图③,和都是等腰直角三角形,,将绕点A逆时针旋转,连结.当时,在旋转过程中,与的面积和是否存在最大值?若存在,写出计算过程;若不存在,请说明理由.
11.如图,将不是矩形的绕点A旋转得到.
(1)当点落在边上,且与边相交于点E时,
①点D____上(填“在”或“不在”);
②如果点、E分别为边、的中点,求的值;
(2)当点落在对角线上,且经过边的中点M时,设,,求y关于x的函数关系式,并写出x的取值范围.
12.如图1,中,,,,将绕点B顺时针旋转得到,其中是点A的对应点,且,连接,.
(1)求证:;
(2)如图2,当点在线段上时,求的面积;
(3)直线与直线交于点D,点E是边的中点,连接,在旋转过程中,求的最大值.
13.在 中,,是斜边的中点,把一三角尺的直角顶点放在点处,以为旋转中心,旋转三角尺,三角尺的两直角边与的两直角边分别交于点,.
(1)求证:;
(2)在旋转三角尺的过程中,四边形的面积大小是否有变化?若没有变化,请求出四边形的面积;若有变化,请说明理由;
(3)连接,在旋转三角尺的过程中,周长的最小值是 .
14.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.
(1)观察猜想:图1中,线段NM、NP的数量关系是 ,∠MNP的大小为 ;
(2)探究证明:把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP、BD、CE,判断△MNP的形状,并说明理由;
(3)拓展延伸:当∠BAC=90°,AB=AC=10,AD=AE=6时,把△ADE绕点A在平面内自由旋转,如图3,请求出△MNP面积的最大值.
15.如图,中,,,点、在边上,,将绕点顺时针旋转得.
(1)求证:;
(2)连接,求证:;
(3)若,,则______,四边形的面积=______.
16.如图1,在中,,,点,分别在边,上,,连接,点,,分别为,,的中点.
(1)观察猜想:图1中,线段与的数量关系是______,位置关系是______;
(2)探究证明:把绕点逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点在平面内自由旋转,若,,请直接写出面积的最大值______.
17.如图,在△ABC中,AB=,∠A=45°,AC=,过点C作直线平行AB,将△ABC绕点A顺时针旋转得到△(点B,C的对应点分别为,),射线,分别交直线于点P、Q.
(1)如图1,求BC的长;
(2)如图2,当点C为PQ中点时,求tan∠APQ;
(3)如图3,当点P,Q分别在线段,上时,试探究四边形的面积是否存在最大值.若存在,求出其最大值;若不存在,请说明理由.
18.定义:两个顶角相等且顶角顶点重合的等腰三角形组合称为“相似等腰组”.如图1,等腰△ABC和等腰△ADE即为“相似等腰组”.
(1)如图2,将上述“相似等腰组”中的△ADE绕看点A逆时针旋转一定角度,判断△ABD和△ACE是否全等,并说明理由;
(2)如图3,等腰△ABC和等腰△ADE是“相似等腰组”,且∠BAC=90°,DC和BE相交于点O,判断DC和BE的位置及大小关系,并说明理由;
(3)如图4,在等边△ABC中,D是△ABC内部一点,且,,,直接写出△ABC的面积.
19.在△ABC中,CA=CB,∠ACB=a,将△CAD绕点C按逆时针方向旋转角a得到△CBE,点A,D的对应点分别为点B,E.
(1)如图1,若A,D,E三点在同一直线上,则∠CDE= (用含a的代数式表示);
(2)如图2,若A,D,E三点在同一直线上,a=60°,过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论;
(3)图3中,若CA=2,CD=2,将△DCE绕点C旋转,当 时,△CAD的面积最大,最大面积是 .
20.问题提出
(1)如图1,在中,,,则面积的最大值是______;
(2)问题探究
如图2,在中,,,.点P是边BC上一点,连接AP,将线段AP绕点P顺时针旋转90°,得线段PE,过点E作交BC于点H,求PH的长.
(3)问题解决
如图3,在中,,,P为边AC上一动点(C点除外).将线段BP绕点P顺时针旋转90°,得线段PE,连接CE,则的面积是否存在最大值?若存在请求出面积的最大值,若不存在请说明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025年中考数学压轴题专练:旋转综合题(面积问题)》参考答案
1.(1),
(2)是等腰直角三角形
(3)
【分析】(1)根据三角形中位线定理得,,,,从而得出,;
(2)首先利用证明,得,,再由(1)同理说明结论成立;
(3)先判断出最大时,的面积最大,进而求出,,即可得出最大,最后用面积公式即可得出结论.
【详解】(1)解:点,是,的中点,
,,
点,是,的中点,
,,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:,;
(2)解:是等腰直角三角形.
理由如下:由旋转知,,
,,
,
,,
利用三角形的中位线得,,,
,
是等腰三角形,
同(1)的方法得,,
,
同(1)的方法得,,
,
,
,
,
,
,
是等腰直角三角形;
(3)解:如图,同(2)的方法得,是等腰直角三角形,连接,
∵,
∴当点三点共线时,最大,
如图:
最大时,的面积最大,
最大,
在中,,,
∴由勾股定理得:,
∵点M为中点,
,
在中,,同上可求,
,
同上可得:,
∴,
.
【点睛】本题是几何变换综合题,主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,三角形中位线定理,三角形的三边关系和旋转的性质等知识,证明是等腰直角三角形是解题的关键.
2.(1)见解析
(2)①,证明见解析;②
(3)
【分析】(1)根据正方形的性质证明四边形是矩形,再得,即可解决问题;
(2)①证明,可得即可;
②先根据正方形的性质得,则,,所以,由得,则,即可证明,于是得,根据四边形的面积的面积正方形的面积,即可解决问题;
(3)延长至点G,使,连接,证明,可得,,所以为等腰直角三角形,所以四边形的面积等腰直角三角形的面积,进而可以解决问题.
【详解】(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴四边形是矩形,
∵,
∴,
∴四边形是正方形;
(2)解:①,
证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
∴;
②∵四边形是正方形,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴的面积的面积,
∴四边形的面积的面积正方形的面积;
(3)解:如图,延长至点G,使,连接,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴为等腰直角三角形,
∵,
∴四边形的面积等腰直角三角形的面积.
【点睛】此题是四边形的综合题,考查正方形的性质,全等三角形的判定与性质,旋转的性质,根据正方形性质求出三角形全等的条件是解题的关键.
3.(1);
(2)是等腰直角三角形,见解析
(3)
【分析】(1)由题可知、均是中位线,由,根据,,,得到,继而得到,结合平行线的性质,得到即可.
(2)先证,转化成(1)证明即可.
(3)由(2)可得,要使面积的最大,只需有最大值,则只需有最大值,根据点A是定点,是定长,判定点D在以A圆心,以4为半径的圆上,根据直径是最大的弦,确定点B,A,D三点共线时,有最大值,且为14,计算的最大值即可.
【详解】(1)∵点M、P、N分别为、、的中点,
∴、均是中位线,
∴,
∴,
∵,
∴,
∵,,,
∴,
∴,,
故答案:;.
(2)是等腰直角三角形,理由如下:
连接,
∵,,,
∴,
∵,
∴,
∴,
∵点M、P、N分别为、、的中点,
∴、均是中位线,
∴,
∴,
∵,
∴
,
∵,
∴
∴,,
故是等腰直角三角形.
(3)由(2)可得,要使面积的最大,只需有最大值,则只需有最大值,
∵点A是定点,是定长,,
∴点D在以A圆心,以4为半径的圆上,
∵直径是最大的弦,
∴点B,A,D三点共线时,且B,D在点A的两侧时,有最大值,且为14,
∴,
∴的最大值为49.
∴面积的最大值为.
【点睛】本题考查了等腰直角三角形的性质,三角形中位线定理,三角形全等的判定和性质,旋转的性质,构造辅助圆求最值,熟练掌握中位线定理,构造辅助圆是解题的关键.
4.(1)
(2)见解析
(3)
【分析】(1)作,根据等腰直角三角形的性质与判定,得到,,在中,应用勾股定理,求出的长,根据平行四边形的性质得到的长,根据等腰直角三角形的性质与判定,即可求解,
(2)连接,,根据全等三角形的性质与判定得到,,,结合旋转的性质得到,,根据平行四边形的判定得到,,根据平行四边形的性质得到的长度,即可求解,
(3)将绕点顺时针旋转,得到,由旋转的性质可得,根据两点之间线段最短,得到,当在线段上时取得最小值,作, 根据等腰直角三角形的判定与性质,得到,在中,应用勾股定理得到,,,,由,得到,
在中,得到,在中,得到,,根据,即可求解,
本题考查了,平行四边形的性质,旋转的性质,等腰直角三角形的性质与判定,勾股定理,全等三角形的性质与判定,解题的关键是:通过旋转得到.
【详解】(1)解:过点作,交延长线于点,
∵,,
∴,,
∴,
∵,
∴,,,
∵,
∴,
在中,,,
∴,
由旋转的性质可得:,,
∴是等腰直角三角形,
∴,
故答案为:,
(2)解:连接,,
∵,,
∴,,
又∵,,
∴,
∴,,
∵,,
∴,,
∴,
∴四边形是平行四边形,
∴,
∴,
∴,
(3)解:将绕点顺时针旋转,得到,连接,
由旋转的性质可得,,,,
∴,
∴,当在线段上时取得最小值,
延长与延长线交于点,过点作于点,连接,
由旋转的性质可得,,,
∵,
∴,,
∴,
在中,,,,
∵,即:,解得:,
在中,,
在中,,
∴,
∴,
故答案为:.
5.(1);(2);(3)
【分析】(1)将绕B点逆时针旋转得到,连接,则为等边三角形,.再由 得到,用勾股定理逆定理得到是直角三角形,,从而得到;
(2)将绕点逆时针旋转得到,得到,证明得到;
(3)证明是等腰直角三角形,,将绕点顺时针旋转得到,连接,则为等腰直角三角形,,再计算得,用勾股定理得到,从而利用全等三角形的性质得到.
【详解】解:(1)如图,将绕B点逆时针旋转得到,连接,则
,,
∴为等边三角形.
∴,
又∵
∴
∴ 是直角三角形,,
(2)由正方形的性质得:,,
如图,将绕点逆时针旋转得到,
,,
∴,
,
∵,,,
(3)∵,,
∴是等腰直角三角形,,
如图,将绕点顺时针旋转得到,连接.
则,,,
为等腰直角三角形.
,
又
【点睛】本题考查正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,等边三角形的判定与性质,旋转的性质,勾股定理及其逆定理等知识,利用旋转作出正确作出辅助线是解题的关键.
6.(1)
(2)
(3)的面积为或
【分析】(1)过点B作,交的延长线于点F,求出,,即可求出的值;
(2)过点D作于点H,过点A作于点G,连结,先证明,得到,进一步推得,然后证明,得到,可知点D在上,由此即可得到答案;
(3)当点E在左上方时,过点C作于点M,过点E作于点N,延长交于点T,设交于点,利用和逐步求出,,,求得,的值,最后再利用相似三角形的性质即可求得答案.
【详解】(1)如图1,过点B作,交的延长线于点F,
,,,
,
,
,
是等腰直角三角形,,
,
,
在中,;
(2)如图2,过点D作于点H,过点A作于点G,连结,
,
,,
,
,
,,
,
,
,
,
,
,
,
又,
,
,
点D在上,
,
,
故答案为:.
(3)当点E在右下方时(如图3),
过点C作于点M,过点E作于点N,延长交于点T,设交于点,
,, ,
,
,, ,
,
,
,
,,
,
,
,
,,
,
,
,
,,
,
,
,
,
,
,
,,
,
,
,
,
解得;
当点E在右下方时(如图4),
同理可求得,,,,
;
综上所述,的面积为或.
【点睛】本题属于几何变换综合题,主要考查了图形的旋转,等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,三角函数的定义等知识,构造全等三角形和相似三角形是解答本题的关键.
7.(1)
(2),见解析
(3)
【分析】(1)由旋转性质和“”可证,即可求解;
(2)由旋转性质和“”可证,可得,由外角的性质可得结论;
(3)先证明是等腰直角三角形,可得,则当点A,点D,点B三点共线时,有最大值,即可求面积最大值.
【详解】(1)解:如图1,,
,
,
,
,
,
,
由旋转得:
,
,
在和中
,
,
,
故答案为:;
(2)解:,
理由如下:如图,设与的交点为点P,
绕点A旋转到如图3所示的位置,,
,
,
在和中,
,
,
,
是的外角,也是的外角,
,
,
;
(3)解: M,P,N分别是,,的中点,
,,
,,
,
,
,
,,,
,
是等腰直角三角形,
,
,,
∴当点A,点D,点B三点共线时,有最大值,即面积有最大值,
的最大值为,
面积的最大值为.
【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,三角形中位线定理,三角形的外角性质,掌握“手拉手”型的旋转模型、线段和最值问题的解法,灵活运性质解决问题是解题的关键.
8.(1)
(2),证明见解析
(3)
【分析】(1)由旋转的性质可得,,即可求解;
(2)由旋转的性质可得,,,可证是等边三角形,由等边三角形的性质可得,即可求解;
(3)如图3中,过点作交的延长线于,设交于.由旋转的性质可得,因为,得出,则点在以为直径的圆上运动,即图中上运动,当,四边形的面积最大,此时,又因为,,得出,因为,则,因为,得出,可得,设,求出,在中,,则,所以,则,求出四边形最大面积.
【详解】(1)解:将绕点按逆时针方向旋转角得到,
,,
,
,
故答案为:;
(2);
理由如下:如图,
将绕点按逆时针方向旋转角得到,
,
,,,
是等边三角形,且,
,
,
,
,,之间的数量关系为;
(3)如图3中,过点作交的延长线于,设交于.
绕点按逆时针方向旋转 得到,
,
,
,
,
点在以为直径的圆上运动,即图中上运动,
当,四边形的面积最大,此时,
,,
,
,
,
,
,
,
设,
则,
,
,
,
四边形最大面积.
【点睛】本题是几何变换综合题,考查了全等三角形的性质,旋转的性质,等边三角形的性质,勾股定理,方程思想.
9.(1)2
(2)
(3),理由见解析
(4)的最大为12
【分析】(1)求出的长度,利用旋转的性质得出,进而求出的长度即可;
(2)过点B作于点M,利用等面积法求出的长度,利用勾股定理求出、的长度,进而求出的长度,从而求出的面积;
(3)连接、,设与相交于点N,与相交于点P,利用和是等腰三角形,且从而得出,然后利用得出,从而得出;
(4)过点C作直线于点H,过点G作直线于点Q,, ,利用得出:当最大时,最大,从而得出当A、B、E三点共线时,最大,从而得出的最大值.
【详解】(1)解:当落在上时,如图所示:
∵四边形是矩形,
∴每个内角都等于,
∵,由勾股定理得:
,
由旋转的性质可知:,
∴,
故答案为:2;
(2)解:当点E落在上时,过点B作于点M,
在中,由勾股定理得:
,
∵是直角三角形,,
∴,
∴,
在中,由勾股定理得:
,
在中,由勾股定理得:
,
∴,
∴;
(3)解:,理由如下:
证明:连接、,设与相交于点N,与相交于点P,
由旋转的性质知:,,
∴在等腰和等腰中得到:,,
∴,
∵,
∴,
即;
(4)解:过点C作直线于点H,过点G作直线于点Q,
∴, ,
∵
∴,
∴当最大时,最大,
在旋转过程中,,
∴,
∴当点三点共线时,,此时最大,
∴的最大值为:.
【点睛】本题主要考查了矩形的性质,旋转的性质,勾股定理以及面积的计算,属于中考压轴题,难度较大,在旋转的过程中,找到变化的量和不变的量,通过分析得出三点共线时.最大是解题的突破口.
10.(1)见解析
(2),见解析
(3)存在,7
【分析】(1)证明 ,即可得出结论;
(2)由等腰直角三角形的性质得 ,则 ,同 (1) 得 ,则 , 然后由等腰直角三角形的性质得 ,即可解决问题;
(3)根据旋转的过程中 的面积始终保持不变,而在旋转的过程中, 的边 始终保持不变,即可解决问题;
【详解】(1)证明:∵,
即 ,
在 和 中,
(2),理由如下:
∵ 是等腰直角三角形,
∴,
∴,
同 (1)得: (SAS),
∴,
∴,
∵ 是等腰直角三角形, 为 中 边上的高,
∴,
∵,
∴;
(3) 与 的面积和存在最大值为7,理由如下:
如图(4)
由旋转可知,在旋转的过程中 的面积始终保持不变 ,
∵ 与 面积的和达到最大,
∴ 面积最大,
∵在旋转的过程中, 始终保持不变, ,
∴ 面积最大时, 点 到 的距离最大,
∴,
∴ 与 面积的和达到的最大值为:
【点睛】此题是三角形综合题,考查了等腰三角形的性质、等腰直角三角形的性质、旋转的性 质以及三角形面积等知识,本题综合性强, 熟练掌握等腰三角形的性质和旋转的性质,证明三角形全等是解题的关键,属于中考常考题型
11.(1)①在;②
(2)
【分析】(1)①先证明,得出,再结合旋转的性质和平行四边形的性质,得出,从而得到D在上;
②设,,,则,利用求出,继而求出,再利用得到即,再消去m得到,从而得到或,检验发现不合题意,取,即;
(2)依然设,,则,作于E,于F,证明得到,从而得到,再证明得到,从而得到,利用,即即得到,至此得解.
【详解】(1)解:①在,理由如下:
旋转的性质可知:,,,
∴,
∴
∴
又∵四边形是平行四边形,
∴
又∵绕点A旋转得到,
∴
∴点D在上,
故答案是:在;
②设,,,则,
∵四边形是平行四边形,
∴,,
又∵点、E分别为边、的中点,
∴,
旋转的性质可知:,,,,
∴,
∴
∴,即,
∴
又∵绕点A旋转得到,
∴,,,
∴.
∵,,
∴
∴,即
由得:
由得:,
∴,
∴即
∴,
∴整理得:,即
∴或
∴或
当时,如下图所示,
则,
∴,
∴,
又∵,
∴,
又∵
∴,
∴(不合题意,舍去)
∴,即
(2)依然设,,则,
根据题意画出图形如下:作于E,于F,
∵经过边的中点M,
∴,
由旋转可知:,
又∵
∴
∵,
∴
∴,即
∴
又∵,
∴
∴,
∴,
由,即得:,即,
∴求y关于x的函数关系式为, x的取值范围为.
【点睛】本题考查旋转的性质,平行四边形的性质,相似三角形的判定与性质,利用相似三角形对应边成比例求线段长是解题的关键.
12.(1)见解析
(2)
(3)4
【分析】(1)通过证明,可得结论;
(2)先求出的面积,由相似三角形的性质可求解;
(3)先确定点D在以为直径的圆上运动,由三角形中位线定理可求的长,即可求解.
【详解】(1)∵在,,,,
∴,
∵将绕点B顺时针旋转得到,
∴
∴,
∴,
∴;
(2)如图2,过点B作于H,
∵将绕点B顺时针旋转得到,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴;
(3)如图3,
∵,
∴,
∵,
∴,
∴,
∴,
∴点D在以为直径的圆上运动,
设的中点为P,
当点P在线段上时,有最大值,
∵,
∴,
∴,
∴DE的最大值为4.
【点睛】本题主要考查相似三角形的判定和性质,旋转的性质,勾股定理等知识,添加恰当辅助线构造直角三角形是解题的关键.
13.(1)证明见解析;
(2)四边形的面积没有变化,为1;
(3)
【分析】(1)过点作于点,作于点,可得四边形是矩形,再证得.可得四边形是正方形,从而得到,即可;
(2)根据,可得,从而得到 ,即可求解;
(3)由(1)得:,从而得到,进而得到,可得到当最小时,的周长最小,为,然后取的中点G连接,,再根据直角三角形的性质可得,即可求解.
【详解】(1)证明:如图,过点作于点,作于点,
.
,
四边形是矩形.
∴, ,,
∴,
,
.
四边形是正方形.
,
.
.
.
(2)解:四边形 的面积没有变化.
由(1)可知 ,
,
四边形是正方形,且,
,
即四边形的面积没有变化,为1;
(3)解:由(1)得:,
∴,
∴,
∴当最小时,的周长最小,为,
如图,取的中点G连接,,
∵,
∴,
∴,
∵是斜边的中点,
∴,
∴在旋转三角尺的过程中,周长的最小值是.
故答案为:
【点睛】本题主要考查了全等三角形的判定和性质,平行线分线段成比例,正方形的判定和性质,直角三角形的性质,根据题意证得是解题的关键.
14.(1)MN=NP,∠MNP=60°;
(2)△MNP是等边三角形,理由见解析;
(3)△MNP面积的最大值是32.
【分析】(1)根据AB=AC,AD=AE,得BD=CE,再根据三角形中位线定理可知MN=BD,PN=CE,MN∥AB,PN∥AC,利用平行线的性质可证得∠MNP=60°;
(2)先通过SAS证明△ABD≌△ACE,得BD=CE,∠ABD=∠ACE,再由(1)同理可证;
(3)由三角形三边关系可知:BD≤8,由题意证得△MNP是等腰直角三角形,MN=BD,则MN最大值为8,即可求得△MNP的最大面积.
【详解】(1)解:∵AB=AC,AD=AE,
∴BD=CE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MN=BD,PN=CE,MN∥AB,PN∥AC,
∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,
∴∠MNE+∠ENP=∠ABE+∠AEB,
∵∠ABE+∠AEB=180° ∠BAE=60°,
∴∠MNP=60°,
故答案为:MN=NP,∠MNP=60°.
(2)△MNP是等边三角形,理由如下:
由旋转得:∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MN=BD,PN=CE,MN∥BD,PN∥CE,
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,
∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB,
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,
∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC ∠ECB=180° ∠BAC=60°,
∴△MNP是等边三角形;
(3)由旋转得:∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MP=EC,PN=BD,MP∥EC,PN∥BD,
∴MP=PN,∠ACE=∠ABD,∠MPD=∠ECD,∠PNC=∠DBC,
∴∠MPD=∠ECA+∠ACD=∠ABD+∠ACD,
∠DPN=∠PCB+∠PNC=∠PCB+∠DBC,
∴∠MPN=∠MPD+∠DPN=∠ABD+∠ACD+∠PCB+∠DBC=∠ABC+∠ACB=180° ∠BAC=90°,
∴△MPN是等腰直角三角形,
由三角形三边关系可知:BD≤AB+AD,
即BD≤16,
PM=,
∴PM=8时,S△MNP最大,
∴S△MNP最大为:×8×8=32.
【点睛】此题是几何变换综合题,主要了旋转的性质,全等三角形的判定与性质,三角形中位线定理,等边三角形的判定,等腰直角三角形的判定等知识,利用平行线的性质求∠MNP的度数是解题的关键.
15.(1)证明见解析
(2)证明见解析
(3);
【分析】(1)由旋转的性质得,从而得到,即可证明结论;
(2)由旋转的性质得,,则,再利用即可证明;
(3)如图,过点作于,由(1)得,,在中,由勾股定理得,则,再根据直角三角形斜边上的中线等于斜边的一半求出,再利用可得出答案.
【详解】(1)证明:∵将绕点顺时针旋转得,
∴,
∵在中,,,
∴,
∴,
∴.
(2)证明:∵将绕点顺时针旋转得,
∴,,
∵,,
∴,
∴,
∴,
在和中,
,
∴.
(3)解:如图,过点作于,
∵将绕点顺时针旋转得,,,
∴,
由(1)得,,
在中,,
由(2)得,,
∴,,
∴,
∵在中,,,
∴,
∴,
∴四边形的面积:
.
故答案为:;.
【点睛】本题主要考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定与性质,勾股定理,等腰三角形三线合一的性质等知识.证明是解题的关键.
16.(1),
(2)等腰直角三角形,理由见解析
(3)8
【分析】(1)利用三角形的中位线得出,,进而判断出,即可得出结论,再利用三角形的中位线得出、PN∥BD得出、∠DPN=∠ADC,最后用互余即可得出结论;
(2)先判断出,得出,同(1)的方法得出,,即可得出,同(1)的方法即可得出结论;
(3)先判断出最大时,的面积最大,而最大是,即可得出结论.
【详解】(1)解:点N,分别是,的中点,
,,
点,是,的中点,
,,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:,;
(2)是等腰直角三角形.理由如下:
由旋转知,,
,,
,
,,
利用三角形的中位线得,,,
,
是等腰三角形,
同(1)的方法得,,
,
同(1)的方法得,,
,
,
,
,
,
,
是等腰直角三角形;
(3)由(2)知,是等腰直角三角形,,
最大时,面积最大,
点在的延长线上时,BD最大,
,
,
故答案为:8
【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质的综合运用;解(1)的关键是判断出,,解(2)的关键是判断出,解(3)的关键是判断出最大时,的面积最大.
17.(1)
(2)
(3)存在;
【分析】(1)过点C作CD⊥AB于D,则可得CD=AD,在Rt△ADC中,由勾股定理,得2AD2=AC2=,即可求得AD=CD=2,则BD=AB-AD=3-2=,在Rt△BDC中,由勾股定理,即可求得BC长;
(2)延长AC至E,使CE=AC,连接PE,过点A作AF⊥l于F,证△ACQ≌△ECP(SAS),得∠E=∠CAQ,从而证得∠BAP=∠CAQ,继而证△APC∽△AEP,得,即可求出AP=4,又因为AF=CD=2,在Rt△AFP中,由勾股定理,求得PF=6,即可由tan∠APQ=求解;
(3)过点P作PH⊥AQ于H,S四边形PQC′B′=S△AB′C′-S△APQ=-=,当AP·AQ取最小值时,取最大值,当AP=AQ时,S四边形PQC′B′的面积取最大值,最大值为:,此时∠APQ=∠AQP=67.5°,旋转角∠BAP=∠CAQ=67.5°,则CQ=AC=,过A作AT⊥CQ于T,则AT=,由勾股定理得:CT=,所以TQ=CQ-CT=-由勾股定理得:AQ2=AT2+TQ2==,即可求出S四边形PQC′B′的最大值.
【详解】(1)解:如图1,过点C作CD⊥AB于D,
∵CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠A=45°,
∴∠ACD=45°,
∴AD=CD,
在Rt△ADC中,由勾股定理,得
2AD2=AC2=,
∴AD=CD=2,
∴BD=AB-AD=3-2=,
在Rt△BDC中,由勾股定理,得
BC=;
(2)解:如图2,延长AC至E,使CE=AC,连接PE,过点A作AF⊥l于F,
当点C为PQ中点时,则PC=CQ,
在△ACQ和△ECP中,
,
∴△ACQ≌△ECP(SAS),
∴∠E=∠CAQ,
∵∠PAC+∠CAQ=∠PAQ=45°,∠BAP+∠PAC=∠BAC=45°,
∴∠BAP=∠CAQ,
∵lAB,
∴∠APC=∠E,
∵∠PAC=∠EAP,
∴△APC∽△AEP,
∴,
∵AC=2,AE=2AC=2×2=4,
∴AP2=ACAE==48,
∴AP=4,
由(1)知,CD=2,CD⊥AB,
∵ABCF,AF⊥CF,
∴四边形ADCF是矩形,
∴AF=CD=2,
在Rt△AFP中,由勾股定理,得PF==6,
∴tan∠APQ=;
(3)解:如图所示,过点P作PH⊥AQ于H,
∴S四边形PQC’B’=S△AB’C’-S△APQ
=-
=
=,
当AP·AQ取最小值时,取最大值.
设a、b是两个正数,则:
即
ab≥,
当且仅当a=b时取等号,此时ab取最小值.
∴S四边形PQC′B′=,
当AP=AQ时,S四边形PQC′B′的面积取最大值,最大值为:,
此时∠APQ=∠AQP=67.5°,旋转角∠BAP=∠CAQ=67.5°,
则CQ=AC=,
过A作AT⊥CQ于T,则AT=,
由勾股定理得:CT=,
∴TQ=CQ-CT=-,
由勾股定理得:AQ2=AT2+TQ2==,
S四边形PQC′B′的面积最大值为:==.
【点睛】本题属旋转综合题目,考查了旋转的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,矩形的判定与性质,三角函数的定义,熟练掌握相关性质和正确作辅助线,转换所求问题是解题的关键.
18.(1)全等;理由见解析
(2);
(3)
【分析】(1)由∠BAC=∠DAE,得∠BAD=∠CAE,利用SAS可证结论;
(2)由(1)同理可证△ABE≌△ACD(SAS),得DC=BE,∠ABE=∠ACD,从而得BE⊥CD;
(3)将△ABD绕点A逆时针旋转60°得△ACE,可证DE2+CE2=CD2,则∠CED=90°,过点C作CF⊥AE,交AE的延长线于F,得CF=CE=2,EF=,在Rt△ACF中,运用勾股定理求出AC的长,从而求出等边△ABC的面积.
【详解】(1)解:全等,理由如下:
∵等腰△ABC和等腰△ADE为“相似等腰组”,
∴∠BAC=∠DAE,
∵∠BAD=∠BAC ∠DAC,∠CAE=∠EAD ∠DAC,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
∴△ABD≌△ACE(SAS);
(2)解:DC⊥BE,DC=BE,理由如下:
∵等腰△ABC和等腰△ADE为“相似等腰组”,
∴∠BAC=∠DAE=90°,
∵∠BAE=∠BAC+∠EAC,∠CAD=∠EAD+∠EAC,
∴∠BAE=∠CAD,
在△ABE与△ACD中,
∴△ABE≌△ACD(SAS),
∴DC=BE,∠ABE=∠ACD,
∵∠ABE+∠EBC+∠ACB=90°,
∴∠ACD+∠EBC+∠ACB=90°,
∴∠EAC+∠DCB=90°,
∴DC⊥BE;
(3)解:将△ABD绕点A逆时针旋转60°得△ACE,如图所示:
∴AD=AE,∠DAE=60°,CE=BD=4,
∴△ADE是等边三角形,
∴DE=AD=3,∠AED=60°,
∵,,
∴,
∴∠CED=90°,
∴∠AEC=∠AED+∠DEC=60°+90°=150°,
过点C作CF⊥AE,交AE的延长线于F,
∴CF=CE=2,EF=,
∴,
在Rt△ACF中,,
∴.
【点睛】本题主要考查了等边三角形的性质,全等三角形的判定与性质,勾股定理以及逆定理等知识,解题的关键是运用旋转将分散条件集中到一个三角形中进行求解.
19.(1)
(2)AE=BE+CF;证明见解析
(3)CD⊥AC;2
【分析】(1)由旋转的性质可得CD=CE,∠DCE=α,即可求解;
(2)由旋转的性质可得AD=BE,CD=CE,∠DCE=60°,可证△CDE是等边三角形,由等边三角形的性质可得DF=EF=CF,即可求解;
(3)过点D作DF⊥AC于点F,当DF取得最大值时,△CAD面积最大,当CD=DF=2时可得出答案.
【详解】(1)解:如图1中,
∵将△CAD绕点C按逆时针方向旋转角α得到△CBE,
∴△ACD≌△BCE,∠DCE=α,
∴CD=CE,
∴∠CDE=.
故答案为:.
(2)解:如图2中,
∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE,
∴△ACD≌△BCE,
∴AD=BE,CD=CE,∠DCE=60°,
∴△CDE是等边三角形,且CF⊥DE,
∴DF=EF=CF,
∵AE=AD+DF+EF,
∴AE=BE+CF.
(3)解:如图,过点D作DF⊥AC于点F,
∵S△ACD=AC DF=DF,
∴当DF取得最大值时,△CAD面积最大,
又∵在△CFD中,DF<CD,
∴只有当CD旋转到与AC垂直时,FD才能取得最大值,即FD=CD=2,
∴△CAD的面积最大,最大面积是2,
故答案为:CD⊥AC;2.
【点睛】本题属于几何变换综合题,考查了等腰三角形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(1)
(2)
(3)存在,最大值为8
【分析】(1)设AC=x,则AB=6-x,表示出△ABC的面积,然后利用二次函数的性质求最大值;
(2)作AG⊥BC于G,利用AAS证明△APG≌△PEH,得PH=AG,再利用含30°角的直角三角形的性质求出AG的长即可;
(3)结合(1)(2)的方法,过点E作EG⊥CA,交CA延长线于G,BH⊥CA,交CA延长线于H,作AD⊥BC于D,首先利用等积法求出BH的长,设CP=x,则AP=6-x,表示出面积,利用二次函数的性质解决问题.
【详解】(1)解:设,则,
,
当时,最大为,
故答案为:;
(2)作于,
将线段绕点顺时针旋转90度,得线段,
,,
,
,
,
,
,
,
,,
,
,
;
(3)的面积存在最大值,理由如下:
过点作,交延长线于,,交延长线于,作于,
由(2)同理知,,
,
,,
,
由勾股定理得,,
,
,
,
在中,,
设,则,
,
的面积为,
当时,的面积最大值为8.
【点睛】本题是三角形综合题,主要考查了旋转的性质,等腰直角三角形的判定与性质,二次函数的性质,全等三角形的判定与性质等知识,构造全等三角形是解题的关键.
中小学教育资源及组卷应用平台
2025年中考数学压轴题专练:旋转综合题(面积问题)
1.如图1,在中,,,点、分别在边、上,,连接,点、、分别为、、的中点.
(1)观察猜想:图1中,线段与的数量关系是 ,位置关系是 ;
(2)探究证明:把绕点A逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点A在平面内自由旋转,若,,直接写出面积的最大值.
2.已知正方形边长为1,对角线相交于点O,过点O作射线,分别交于点E,F,且.
(1)如图1,当时,求证:四边形是正方形;
(2)如图2,将射线绕着点O进行旋转.
①在旋转过程中,判断线段与的数量关系,并给出证明;
②四边形的面积为 ;
(3)如图3,在四边形中,,连接.若,请直接写出四边形的面积.
3.如图1,在等腰中,,点D、E分别在边、上,,连接,点M、P、N分别为、、的中点.
(1)观察猜想:
图1中,线段与的数量关系是______,位置关系是______;
(2)探究证明:
把绕点A逆时针方向旋转到图2的位置,连接,,判断的形状,并说明理由;
(3)拓展延伸:
把绕点A在平面内自由旋转,若,,求面积的最大值.
4.在中,,连接,已知,点E在线段上,将线段绕点D顺时针旋转 为线段.
(1)如图1,线段与线段的交点和点E重合,连接,求线段的长度;
(2)如图2,点G为延长线上一点,使得,连接交于点H,求证:;
(3)如图3,在(2)的条件下,平面内一点P,当最小时,求的面积.
5.【问题初探】(1)如图1,为等边三角形内一点,满足,,,试求的大小.李明同学的思路是:将绕点逆时针旋转60°,点的对应点为,画出旋转后的图形,再连接.将求分成求和的和即可.请你按照李明同学给出的旋转的思路,求的大小;
【问题解决】(2)如图2,在正方形中,,分别为,边上的点,满足,若,,求的面积;
【问题拓展】(3)如图3,在四边形,,,,求的长.
6.在和中,,,,若,.
(1)如图1,当点在线段上时,连接,求;
(2)如图2.将图1中绕着点旋转,使点在的内部,连接,.线段,相交于点,且,此时_______;
(3)如图3,在绕着点旋转过程中,当点落在线段上时,过点作交直线于点,直接写出的面积.
7.综合与实践
图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图1,在中,,,D,E分别为,边上一点,连接,且,将绕点A在平面内旋转.
(1)观察猜想
若,将绕点A旋转到如图2所示的位置,则与的数量关系为 ;
(2)类比探究
若,将绕点A旋转到如图3所示的位置,,相交于点O,猜想,满足的位置关系,并说明理由;
(3)拓展应用
如图4,在(2)的条件下,连结,分别取,,的中点M,P,N,连结,,,若,,请直接写出在旋转过程中面积的最大值.
8.如图1,中,,,为内一点,将绕点按逆时针方向旋转角得到,点,的对应点分别为点,,且,,三点在同一直线上.
(1)填空: ;(用含α的代数式表示)
(2)如图2,若,请补全图形,再过点作于点,然后探究线段,,之间的数量关系,并证明你的结论;
(3)如图3,若,,求四边形面积的最大值.
9.如图1,矩形中,,,将矩形绕着点B顺时针旋转,得到矩形.
(1)当点E落在上时,则线段的长度等于 ;
(2)如图2,当点E落在上时,求的面积;
(3)如图3,连接、、、,判断线段与的位置关系且说明理由;
(4)在旋转过程中,请直接写出的最大值.
10.已知和都是等腰三角形,.
(1)如图①,当点D在外部,点E在内部时,求证:.
(2)如图②,和都是等腰直角三角形,,点C,D,E在同一直线上,为中边上的高.求的度数;判断线段之间的数量关系,并说明理由.
(3)如图③,和都是等腰直角三角形,,将绕点A逆时针旋转,连结.当时,在旋转过程中,与的面积和是否存在最大值?若存在,写出计算过程;若不存在,请说明理由.
11.如图,将不是矩形的绕点A旋转得到.
(1)当点落在边上,且与边相交于点E时,
①点D____上(填“在”或“不在”);
②如果点、E分别为边、的中点,求的值;
(2)当点落在对角线上,且经过边的中点M时,设,,求y关于x的函数关系式,并写出x的取值范围.
12.如图1,中,,,,将绕点B顺时针旋转得到,其中是点A的对应点,且,连接,.
(1)求证:;
(2)如图2,当点在线段上时,求的面积;
(3)直线与直线交于点D,点E是边的中点,连接,在旋转过程中,求的最大值.
13.在 中,,是斜边的中点,把一三角尺的直角顶点放在点处,以为旋转中心,旋转三角尺,三角尺的两直角边与的两直角边分别交于点,.
(1)求证:;
(2)在旋转三角尺的过程中,四边形的面积大小是否有变化?若没有变化,请求出四边形的面积;若有变化,请说明理由;
(3)连接,在旋转三角尺的过程中,周长的最小值是 .
14.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.
(1)观察猜想:图1中,线段NM、NP的数量关系是 ,∠MNP的大小为 ;
(2)探究证明:把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP、BD、CE,判断△MNP的形状,并说明理由;
(3)拓展延伸:当∠BAC=90°,AB=AC=10,AD=AE=6时,把△ADE绕点A在平面内自由旋转,如图3,请求出△MNP面积的最大值.
15.如图,中,,,点、在边上,,将绕点顺时针旋转得.
(1)求证:;
(2)连接,求证:;
(3)若,,则______,四边形的面积=______.
16.如图1,在中,,,点,分别在边,上,,连接,点,,分别为,,的中点.
(1)观察猜想:图1中,线段与的数量关系是______,位置关系是______;
(2)探究证明:把绕点逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点在平面内自由旋转,若,,请直接写出面积的最大值______.
17.如图,在△ABC中,AB=,∠A=45°,AC=,过点C作直线平行AB,将△ABC绕点A顺时针旋转得到△(点B,C的对应点分别为,),射线,分别交直线于点P、Q.
(1)如图1,求BC的长;
(2)如图2,当点C为PQ中点时,求tan∠APQ;
(3)如图3,当点P,Q分别在线段,上时,试探究四边形的面积是否存在最大值.若存在,求出其最大值;若不存在,请说明理由.
18.定义:两个顶角相等且顶角顶点重合的等腰三角形组合称为“相似等腰组”.如图1,等腰△ABC和等腰△ADE即为“相似等腰组”.
(1)如图2,将上述“相似等腰组”中的△ADE绕看点A逆时针旋转一定角度,判断△ABD和△ACE是否全等,并说明理由;
(2)如图3,等腰△ABC和等腰△ADE是“相似等腰组”,且∠BAC=90°,DC和BE相交于点O,判断DC和BE的位置及大小关系,并说明理由;
(3)如图4,在等边△ABC中,D是△ABC内部一点,且,,,直接写出△ABC的面积.
19.在△ABC中,CA=CB,∠ACB=a,将△CAD绕点C按逆时针方向旋转角a得到△CBE,点A,D的对应点分别为点B,E.
(1)如图1,若A,D,E三点在同一直线上,则∠CDE= (用含a的代数式表示);
(2)如图2,若A,D,E三点在同一直线上,a=60°,过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论;
(3)图3中,若CA=2,CD=2,将△DCE绕点C旋转,当 时,△CAD的面积最大,最大面积是 .
20.问题提出
(1)如图1,在中,,,则面积的最大值是______;
(2)问题探究
如图2,在中,,,.点P是边BC上一点,连接AP,将线段AP绕点P顺时针旋转90°,得线段PE,过点E作交BC于点H,求PH的长.
(3)问题解决
如图3,在中,,,P为边AC上一动点(C点除外).将线段BP绕点P顺时针旋转90°,得线段PE,连接CE,则的面积是否存在最大值?若存在请求出面积的最大值,若不存在请说明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025年中考数学压轴题专练:旋转综合题(面积问题)》参考答案
1.(1),
(2)是等腰直角三角形
(3)
【分析】(1)根据三角形中位线定理得,,,,从而得出,;
(2)首先利用证明,得,,再由(1)同理说明结论成立;
(3)先判断出最大时,的面积最大,进而求出,,即可得出最大,最后用面积公式即可得出结论.
【详解】(1)解:点,是,的中点,
,,
点,是,的中点,
,,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:,;
(2)解:是等腰直角三角形.
理由如下:由旋转知,,
,,
,
,,
利用三角形的中位线得,,,
,
是等腰三角形,
同(1)的方法得,,
,
同(1)的方法得,,
,
,
,
,
,
,
是等腰直角三角形;
(3)解:如图,同(2)的方法得,是等腰直角三角形,连接,
∵,
∴当点三点共线时,最大,
如图:
最大时,的面积最大,
最大,
在中,,,
∴由勾股定理得:,
∵点M为中点,
,
在中,,同上可求,
,
同上可得:,
∴,
.
【点睛】本题是几何变换综合题,主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,三角形中位线定理,三角形的三边关系和旋转的性质等知识,证明是等腰直角三角形是解题的关键.
2.(1)见解析
(2)①,证明见解析;②
(3)
【分析】(1)根据正方形的性质证明四边形是矩形,再得,即可解决问题;
(2)①证明,可得即可;
②先根据正方形的性质得,则,,所以,由得,则,即可证明,于是得,根据四边形的面积的面积正方形的面积,即可解决问题;
(3)延长至点G,使,连接,证明,可得,,所以为等腰直角三角形,所以四边形的面积等腰直角三角形的面积,进而可以解决问题.
【详解】(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴四边形是矩形,
∵,
∴,
∴四边形是正方形;
(2)解:①,
证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
∴;
②∵四边形是正方形,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴的面积的面积,
∴四边形的面积的面积正方形的面积;
(3)解:如图,延长至点G,使,连接,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴为等腰直角三角形,
∵,
∴四边形的面积等腰直角三角形的面积.
【点睛】此题是四边形的综合题,考查正方形的性质,全等三角形的判定与性质,旋转的性质,根据正方形性质求出三角形全等的条件是解题的关键.
3.(1);
(2)是等腰直角三角形,见解析
(3)
【分析】(1)由题可知、均是中位线,由,根据,,,得到,继而得到,结合平行线的性质,得到即可.
(2)先证,转化成(1)证明即可.
(3)由(2)可得,要使面积的最大,只需有最大值,则只需有最大值,根据点A是定点,是定长,判定点D在以A圆心,以4为半径的圆上,根据直径是最大的弦,确定点B,A,D三点共线时,有最大值,且为14,计算的最大值即可.
【详解】(1)∵点M、P、N分别为、、的中点,
∴、均是中位线,
∴,
∴,
∵,
∴,
∵,,,
∴,
∴,,
故答案:;.
(2)是等腰直角三角形,理由如下:
连接,
∵,,,
∴,
∵,
∴,
∴,
∵点M、P、N分别为、、的中点,
∴、均是中位线,
∴,
∴,
∵,
∴
,
∵,
∴
∴,,
故是等腰直角三角形.
(3)由(2)可得,要使面积的最大,只需有最大值,则只需有最大值,
∵点A是定点,是定长,,
∴点D在以A圆心,以4为半径的圆上,
∵直径是最大的弦,
∴点B,A,D三点共线时,且B,D在点A的两侧时,有最大值,且为14,
∴,
∴的最大值为49.
∴面积的最大值为.
【点睛】本题考查了等腰直角三角形的性质,三角形中位线定理,三角形全等的判定和性质,旋转的性质,构造辅助圆求最值,熟练掌握中位线定理,构造辅助圆是解题的关键.
4.(1)
(2)见解析
(3)
【分析】(1)作,根据等腰直角三角形的性质与判定,得到,,在中,应用勾股定理,求出的长,根据平行四边形的性质得到的长,根据等腰直角三角形的性质与判定,即可求解,
(2)连接,,根据全等三角形的性质与判定得到,,,结合旋转的性质得到,,根据平行四边形的判定得到,,根据平行四边形的性质得到的长度,即可求解,
(3)将绕点顺时针旋转,得到,由旋转的性质可得,根据两点之间线段最短,得到,当在线段上时取得最小值,作, 根据等腰直角三角形的判定与性质,得到,在中,应用勾股定理得到,,,,由,得到,
在中,得到,在中,得到,,根据,即可求解,
本题考查了,平行四边形的性质,旋转的性质,等腰直角三角形的性质与判定,勾股定理,全等三角形的性质与判定,解题的关键是:通过旋转得到.
【详解】(1)解:过点作,交延长线于点,
∵,,
∴,,
∴,
∵,
∴,,,
∵,
∴,
在中,,,
∴,
由旋转的性质可得:,,
∴是等腰直角三角形,
∴,
故答案为:,
(2)解:连接,,
∵,,
∴,,
又∵,,
∴,
∴,,
∵,,
∴,,
∴,
∴四边形是平行四边形,
∴,
∴,
∴,
(3)解:将绕点顺时针旋转,得到,连接,
由旋转的性质可得,,,,
∴,
∴,当在线段上时取得最小值,
延长与延长线交于点,过点作于点,连接,
由旋转的性质可得,,,
∵,
∴,,
∴,
在中,,,,
∵,即:,解得:,
在中,,
在中,,
∴,
∴,
故答案为:.
5.(1);(2);(3)
【分析】(1)将绕B点逆时针旋转得到,连接,则为等边三角形,.再由 得到,用勾股定理逆定理得到是直角三角形,,从而得到;
(2)将绕点逆时针旋转得到,得到,证明得到;
(3)证明是等腰直角三角形,,将绕点顺时针旋转得到,连接,则为等腰直角三角形,,再计算得,用勾股定理得到,从而利用全等三角形的性质得到.
【详解】解:(1)如图,将绕B点逆时针旋转得到,连接,则
,,
∴为等边三角形.
∴,
又∵
∴
∴ 是直角三角形,,
(2)由正方形的性质得:,,
如图,将绕点逆时针旋转得到,
,,
∴,
,
∵,,,
(3)∵,,
∴是等腰直角三角形,,
如图,将绕点顺时针旋转得到,连接.
则,,,
为等腰直角三角形.
,
又
【点睛】本题考查正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,等边三角形的判定与性质,旋转的性质,勾股定理及其逆定理等知识,利用旋转作出正确作出辅助线是解题的关键.
6.(1)
(2)
(3)的面积为或
【分析】(1)过点B作,交的延长线于点F,求出,,即可求出的值;
(2)过点D作于点H,过点A作于点G,连结,先证明,得到,进一步推得,然后证明,得到,可知点D在上,由此即可得到答案;
(3)当点E在左上方时,过点C作于点M,过点E作于点N,延长交于点T,设交于点,利用和逐步求出,,,求得,的值,最后再利用相似三角形的性质即可求得答案.
【详解】(1)如图1,过点B作,交的延长线于点F,
,,,
,
,
,
是等腰直角三角形,,
,
,
在中,;
(2)如图2,过点D作于点H,过点A作于点G,连结,
,
,,
,
,
,,
,
,
,
,
,
,
,
又,
,
,
点D在上,
,
,
故答案为:.
(3)当点E在右下方时(如图3),
过点C作于点M,过点E作于点N,延长交于点T,设交于点,
,, ,
,
,, ,
,
,
,
,,
,
,
,
,,
,
,
,
,,
,
,
,
,
,
,
,,
,
,
,
,
解得;
当点E在右下方时(如图4),
同理可求得,,,,
;
综上所述,的面积为或.
【点睛】本题属于几何变换综合题,主要考查了图形的旋转,等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,三角函数的定义等知识,构造全等三角形和相似三角形是解答本题的关键.
7.(1)
(2),见解析
(3)
【分析】(1)由旋转性质和“”可证,即可求解;
(2)由旋转性质和“”可证,可得,由外角的性质可得结论;
(3)先证明是等腰直角三角形,可得,则当点A,点D,点B三点共线时,有最大值,即可求面积最大值.
【详解】(1)解:如图1,,
,
,
,
,
,
,
由旋转得:
,
,
在和中
,
,
,
故答案为:;
(2)解:,
理由如下:如图,设与的交点为点P,
绕点A旋转到如图3所示的位置,,
,
,
在和中,
,
,
,
是的外角,也是的外角,
,
,
;
(3)解: M,P,N分别是,,的中点,
,,
,,
,
,
,
,,,
,
是等腰直角三角形,
,
,,
∴当点A,点D,点B三点共线时,有最大值,即面积有最大值,
的最大值为,
面积的最大值为.
【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,三角形中位线定理,三角形的外角性质,掌握“手拉手”型的旋转模型、线段和最值问题的解法,灵活运性质解决问题是解题的关键.
8.(1)
(2),证明见解析
(3)
【分析】(1)由旋转的性质可得,,即可求解;
(2)由旋转的性质可得,,,可证是等边三角形,由等边三角形的性质可得,即可求解;
(3)如图3中,过点作交的延长线于,设交于.由旋转的性质可得,因为,得出,则点在以为直径的圆上运动,即图中上运动,当,四边形的面积最大,此时,又因为,,得出,因为,则,因为,得出,可得,设,求出,在中,,则,所以,则,求出四边形最大面积.
【详解】(1)解:将绕点按逆时针方向旋转角得到,
,,
,
,
故答案为:;
(2);
理由如下:如图,
将绕点按逆时针方向旋转角得到,
,
,,,
是等边三角形,且,
,
,
,
,,之间的数量关系为;
(3)如图3中,过点作交的延长线于,设交于.
绕点按逆时针方向旋转 得到,
,
,
,
,
点在以为直径的圆上运动,即图中上运动,
当,四边形的面积最大,此时,
,,
,
,
,
,
,
,
设,
则,
,
,
,
四边形最大面积.
【点睛】本题是几何变换综合题,考查了全等三角形的性质,旋转的性质,等边三角形的性质,勾股定理,方程思想.
9.(1)2
(2)
(3),理由见解析
(4)的最大为12
【分析】(1)求出的长度,利用旋转的性质得出,进而求出的长度即可;
(2)过点B作于点M,利用等面积法求出的长度,利用勾股定理求出、的长度,进而求出的长度,从而求出的面积;
(3)连接、,设与相交于点N,与相交于点P,利用和是等腰三角形,且从而得出,然后利用得出,从而得出;
(4)过点C作直线于点H,过点G作直线于点Q,, ,利用得出:当最大时,最大,从而得出当A、B、E三点共线时,最大,从而得出的最大值.
【详解】(1)解:当落在上时,如图所示:
∵四边形是矩形,
∴每个内角都等于,
∵,由勾股定理得:
,
由旋转的性质可知:,
∴,
故答案为:2;
(2)解:当点E落在上时,过点B作于点M,
在中,由勾股定理得:
,
∵是直角三角形,,
∴,
∴,
在中,由勾股定理得:
,
在中,由勾股定理得:
,
∴,
∴;
(3)解:,理由如下:
证明:连接、,设与相交于点N,与相交于点P,
由旋转的性质知:,,
∴在等腰和等腰中得到:,,
∴,
∵,
∴,
即;
(4)解:过点C作直线于点H,过点G作直线于点Q,
∴, ,
∵
∴,
∴当最大时,最大,
在旋转过程中,,
∴,
∴当点三点共线时,,此时最大,
∴的最大值为:.
【点睛】本题主要考查了矩形的性质,旋转的性质,勾股定理以及面积的计算,属于中考压轴题,难度较大,在旋转的过程中,找到变化的量和不变的量,通过分析得出三点共线时.最大是解题的突破口.
10.(1)见解析
(2),见解析
(3)存在,7
【分析】(1)证明 ,即可得出结论;
(2)由等腰直角三角形的性质得 ,则 ,同 (1) 得 ,则 , 然后由等腰直角三角形的性质得 ,即可解决问题;
(3)根据旋转的过程中 的面积始终保持不变,而在旋转的过程中, 的边 始终保持不变,即可解决问题;
【详解】(1)证明:∵,
即 ,
在 和 中,
(2),理由如下:
∵ 是等腰直角三角形,
∴,
∴,
同 (1)得: (SAS),
∴,
∴,
∵ 是等腰直角三角形, 为 中 边上的高,
∴,
∵,
∴;
(3) 与 的面积和存在最大值为7,理由如下:
如图(4)
由旋转可知,在旋转的过程中 的面积始终保持不变 ,
∵ 与 面积的和达到最大,
∴ 面积最大,
∵在旋转的过程中, 始终保持不变, ,
∴ 面积最大时, 点 到 的距离最大,
∴,
∴ 与 面积的和达到的最大值为:
【点睛】此题是三角形综合题,考查了等腰三角形的性质、等腰直角三角形的性质、旋转的性 质以及三角形面积等知识,本题综合性强, 熟练掌握等腰三角形的性质和旋转的性质,证明三角形全等是解题的关键,属于中考常考题型
11.(1)①在;②
(2)
【分析】(1)①先证明,得出,再结合旋转的性质和平行四边形的性质,得出,从而得到D在上;
②设,,,则,利用求出,继而求出,再利用得到即,再消去m得到,从而得到或,检验发现不合题意,取,即;
(2)依然设,,则,作于E,于F,证明得到,从而得到,再证明得到,从而得到,利用,即即得到,至此得解.
【详解】(1)解:①在,理由如下:
旋转的性质可知:,,,
∴,
∴
∴
又∵四边形是平行四边形,
∴
又∵绕点A旋转得到,
∴
∴点D在上,
故答案是:在;
②设,,,则,
∵四边形是平行四边形,
∴,,
又∵点、E分别为边、的中点,
∴,
旋转的性质可知:,,,,
∴,
∴
∴,即,
∴
又∵绕点A旋转得到,
∴,,,
∴.
∵,,
∴
∴,即
由得:
由得:,
∴,
∴即
∴,
∴整理得:,即
∴或
∴或
当时,如下图所示,
则,
∴,
∴,
又∵,
∴,
又∵
∴,
∴(不合题意,舍去)
∴,即
(2)依然设,,则,
根据题意画出图形如下:作于E,于F,
∵经过边的中点M,
∴,
由旋转可知:,
又∵
∴
∵,
∴
∴,即
∴
又∵,
∴
∴,
∴,
由,即得:,即,
∴求y关于x的函数关系式为, x的取值范围为.
【点睛】本题考查旋转的性质,平行四边形的性质,相似三角形的判定与性质,利用相似三角形对应边成比例求线段长是解题的关键.
12.(1)见解析
(2)
(3)4
【分析】(1)通过证明,可得结论;
(2)先求出的面积,由相似三角形的性质可求解;
(3)先确定点D在以为直径的圆上运动,由三角形中位线定理可求的长,即可求解.
【详解】(1)∵在,,,,
∴,
∵将绕点B顺时针旋转得到,
∴
∴,
∴,
∴;
(2)如图2,过点B作于H,
∵将绕点B顺时针旋转得到,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴;
(3)如图3,
∵,
∴,
∵,
∴,
∴,
∴,
∴点D在以为直径的圆上运动,
设的中点为P,
当点P在线段上时,有最大值,
∵,
∴,
∴,
∴DE的最大值为4.
【点睛】本题主要考查相似三角形的判定和性质,旋转的性质,勾股定理等知识,添加恰当辅助线构造直角三角形是解题的关键.
13.(1)证明见解析;
(2)四边形的面积没有变化,为1;
(3)
【分析】(1)过点作于点,作于点,可得四边形是矩形,再证得.可得四边形是正方形,从而得到,即可;
(2)根据,可得,从而得到 ,即可求解;
(3)由(1)得:,从而得到,进而得到,可得到当最小时,的周长最小,为,然后取的中点G连接,,再根据直角三角形的性质可得,即可求解.
【详解】(1)证明:如图,过点作于点,作于点,
.
,
四边形是矩形.
∴, ,,
∴,
,
.
四边形是正方形.
,
.
.
.
(2)解:四边形 的面积没有变化.
由(1)可知 ,
,
四边形是正方形,且,
,
即四边形的面积没有变化,为1;
(3)解:由(1)得:,
∴,
∴,
∴当最小时,的周长最小,为,
如图,取的中点G连接,,
∵,
∴,
∴,
∵是斜边的中点,
∴,
∴在旋转三角尺的过程中,周长的最小值是.
故答案为:
【点睛】本题主要考查了全等三角形的判定和性质,平行线分线段成比例,正方形的判定和性质,直角三角形的性质,根据题意证得是解题的关键.
14.(1)MN=NP,∠MNP=60°;
(2)△MNP是等边三角形,理由见解析;
(3)△MNP面积的最大值是32.
【分析】(1)根据AB=AC,AD=AE,得BD=CE,再根据三角形中位线定理可知MN=BD,PN=CE,MN∥AB,PN∥AC,利用平行线的性质可证得∠MNP=60°;
(2)先通过SAS证明△ABD≌△ACE,得BD=CE,∠ABD=∠ACE,再由(1)同理可证;
(3)由三角形三边关系可知:BD≤8,由题意证得△MNP是等腰直角三角形,MN=BD,则MN最大值为8,即可求得△MNP的最大面积.
【详解】(1)解:∵AB=AC,AD=AE,
∴BD=CE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MN=BD,PN=CE,MN∥AB,PN∥AC,
∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,
∴∠MNE+∠ENP=∠ABE+∠AEB,
∵∠ABE+∠AEB=180° ∠BAE=60°,
∴∠MNP=60°,
故答案为:MN=NP,∠MNP=60°.
(2)△MNP是等边三角形,理由如下:
由旋转得:∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MN=BD,PN=CE,MN∥BD,PN∥CE,
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,
∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB,
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,
∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC ∠ECB=180° ∠BAC=60°,
∴△MNP是等边三角形;
(3)由旋转得:∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M、N、P分别为DE、BE、BC的中点,
∴MP=EC,PN=BD,MP∥EC,PN∥BD,
∴MP=PN,∠ACE=∠ABD,∠MPD=∠ECD,∠PNC=∠DBC,
∴∠MPD=∠ECA+∠ACD=∠ABD+∠ACD,
∠DPN=∠PCB+∠PNC=∠PCB+∠DBC,
∴∠MPN=∠MPD+∠DPN=∠ABD+∠ACD+∠PCB+∠DBC=∠ABC+∠ACB=180° ∠BAC=90°,
∴△MPN是等腰直角三角形,
由三角形三边关系可知:BD≤AB+AD,
即BD≤16,
PM=,
∴PM=8时,S△MNP最大,
∴S△MNP最大为:×8×8=32.
【点睛】此题是几何变换综合题,主要了旋转的性质,全等三角形的判定与性质,三角形中位线定理,等边三角形的判定,等腰直角三角形的判定等知识,利用平行线的性质求∠MNP的度数是解题的关键.
15.(1)证明见解析
(2)证明见解析
(3);
【分析】(1)由旋转的性质得,从而得到,即可证明结论;
(2)由旋转的性质得,,则,再利用即可证明;
(3)如图,过点作于,由(1)得,,在中,由勾股定理得,则,再根据直角三角形斜边上的中线等于斜边的一半求出,再利用可得出答案.
【详解】(1)证明:∵将绕点顺时针旋转得,
∴,
∵在中,,,
∴,
∴,
∴.
(2)证明:∵将绕点顺时针旋转得,
∴,,
∵,,
∴,
∴,
∴,
在和中,
,
∴.
(3)解:如图,过点作于,
∵将绕点顺时针旋转得,,,
∴,
由(1)得,,
在中,,
由(2)得,,
∴,,
∴,
∵在中,,,
∴,
∴,
∴四边形的面积:
.
故答案为:;.
【点睛】本题主要考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定与性质,勾股定理,等腰三角形三线合一的性质等知识.证明是解题的关键.
16.(1),
(2)等腰直角三角形,理由见解析
(3)8
【分析】(1)利用三角形的中位线得出,,进而判断出,即可得出结论,再利用三角形的中位线得出、PN∥BD得出、∠DPN=∠ADC,最后用互余即可得出结论;
(2)先判断出,得出,同(1)的方法得出,,即可得出,同(1)的方法即可得出结论;
(3)先判断出最大时,的面积最大,而最大是,即可得出结论.
【详解】(1)解:点N,分别是,的中点,
,,
点,是,的中点,
,,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:,;
(2)是等腰直角三角形.理由如下:
由旋转知,,
,,
,
,,
利用三角形的中位线得,,,
,
是等腰三角形,
同(1)的方法得,,
,
同(1)的方法得,,
,
,
,
,
,
,
是等腰直角三角形;
(3)由(2)知,是等腰直角三角形,,
最大时,面积最大,
点在的延长线上时,BD最大,
,
,
故答案为:8
【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质的综合运用;解(1)的关键是判断出,,解(2)的关键是判断出,解(3)的关键是判断出最大时,的面积最大.
17.(1)
(2)
(3)存在;
【分析】(1)过点C作CD⊥AB于D,则可得CD=AD,在Rt△ADC中,由勾股定理,得2AD2=AC2=,即可求得AD=CD=2,则BD=AB-AD=3-2=,在Rt△BDC中,由勾股定理,即可求得BC长;
(2)延长AC至E,使CE=AC,连接PE,过点A作AF⊥l于F,证△ACQ≌△ECP(SAS),得∠E=∠CAQ,从而证得∠BAP=∠CAQ,继而证△APC∽△AEP,得,即可求出AP=4,又因为AF=CD=2,在Rt△AFP中,由勾股定理,求得PF=6,即可由tan∠APQ=求解;
(3)过点P作PH⊥AQ于H,S四边形PQC′B′=S△AB′C′-S△APQ=-=,当AP·AQ取最小值时,取最大值,当AP=AQ时,S四边形PQC′B′的面积取最大值,最大值为:,此时∠APQ=∠AQP=67.5°,旋转角∠BAP=∠CAQ=67.5°,则CQ=AC=,过A作AT⊥CQ于T,则AT=,由勾股定理得:CT=,所以TQ=CQ-CT=-由勾股定理得:AQ2=AT2+TQ2==,即可求出S四边形PQC′B′的最大值.
【详解】(1)解:如图1,过点C作CD⊥AB于D,
∵CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠A=45°,
∴∠ACD=45°,
∴AD=CD,
在Rt△ADC中,由勾股定理,得
2AD2=AC2=,
∴AD=CD=2,
∴BD=AB-AD=3-2=,
在Rt△BDC中,由勾股定理,得
BC=;
(2)解:如图2,延长AC至E,使CE=AC,连接PE,过点A作AF⊥l于F,
当点C为PQ中点时,则PC=CQ,
在△ACQ和△ECP中,
,
∴△ACQ≌△ECP(SAS),
∴∠E=∠CAQ,
∵∠PAC+∠CAQ=∠PAQ=45°,∠BAP+∠PAC=∠BAC=45°,
∴∠BAP=∠CAQ,
∵lAB,
∴∠APC=∠E,
∵∠PAC=∠EAP,
∴△APC∽△AEP,
∴,
∵AC=2,AE=2AC=2×2=4,
∴AP2=ACAE==48,
∴AP=4,
由(1)知,CD=2,CD⊥AB,
∵ABCF,AF⊥CF,
∴四边形ADCF是矩形,
∴AF=CD=2,
在Rt△AFP中,由勾股定理,得PF==6,
∴tan∠APQ=;
(3)解:如图所示,过点P作PH⊥AQ于H,
∴S四边形PQC’B’=S△AB’C’-S△APQ
=-
=
=,
当AP·AQ取最小值时,取最大值.
设a、b是两个正数,则:
即
ab≥,
当且仅当a=b时取等号,此时ab取最小值.
∴S四边形PQC′B′=,
当AP=AQ时,S四边形PQC′B′的面积取最大值,最大值为:,
此时∠APQ=∠AQP=67.5°,旋转角∠BAP=∠CAQ=67.5°,
则CQ=AC=,
过A作AT⊥CQ于T,则AT=,
由勾股定理得:CT=,
∴TQ=CQ-CT=-,
由勾股定理得:AQ2=AT2+TQ2==,
S四边形PQC′B′的面积最大值为:==.
【点睛】本题属旋转综合题目,考查了旋转的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,矩形的判定与性质,三角函数的定义,熟练掌握相关性质和正确作辅助线,转换所求问题是解题的关键.
18.(1)全等;理由见解析
(2);
(3)
【分析】(1)由∠BAC=∠DAE,得∠BAD=∠CAE,利用SAS可证结论;
(2)由(1)同理可证△ABE≌△ACD(SAS),得DC=BE,∠ABE=∠ACD,从而得BE⊥CD;
(3)将△ABD绕点A逆时针旋转60°得△ACE,可证DE2+CE2=CD2,则∠CED=90°,过点C作CF⊥AE,交AE的延长线于F,得CF=CE=2,EF=,在Rt△ACF中,运用勾股定理求出AC的长,从而求出等边△ABC的面积.
【详解】(1)解:全等,理由如下:
∵等腰△ABC和等腰△ADE为“相似等腰组”,
∴∠BAC=∠DAE,
∵∠BAD=∠BAC ∠DAC,∠CAE=∠EAD ∠DAC,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
∴△ABD≌△ACE(SAS);
(2)解:DC⊥BE,DC=BE,理由如下:
∵等腰△ABC和等腰△ADE为“相似等腰组”,
∴∠BAC=∠DAE=90°,
∵∠BAE=∠BAC+∠EAC,∠CAD=∠EAD+∠EAC,
∴∠BAE=∠CAD,
在△ABE与△ACD中,
∴△ABE≌△ACD(SAS),
∴DC=BE,∠ABE=∠ACD,
∵∠ABE+∠EBC+∠ACB=90°,
∴∠ACD+∠EBC+∠ACB=90°,
∴∠EAC+∠DCB=90°,
∴DC⊥BE;
(3)解:将△ABD绕点A逆时针旋转60°得△ACE,如图所示:
∴AD=AE,∠DAE=60°,CE=BD=4,
∴△ADE是等边三角形,
∴DE=AD=3,∠AED=60°,
∵,,
∴,
∴∠CED=90°,
∴∠AEC=∠AED+∠DEC=60°+90°=150°,
过点C作CF⊥AE,交AE的延长线于F,
∴CF=CE=2,EF=,
∴,
在Rt△ACF中,,
∴.
【点睛】本题主要考查了等边三角形的性质,全等三角形的判定与性质,勾股定理以及逆定理等知识,解题的关键是运用旋转将分散条件集中到一个三角形中进行求解.
19.(1)
(2)AE=BE+CF;证明见解析
(3)CD⊥AC;2
【分析】(1)由旋转的性质可得CD=CE,∠DCE=α,即可求解;
(2)由旋转的性质可得AD=BE,CD=CE,∠DCE=60°,可证△CDE是等边三角形,由等边三角形的性质可得DF=EF=CF,即可求解;
(3)过点D作DF⊥AC于点F,当DF取得最大值时,△CAD面积最大,当CD=DF=2时可得出答案.
【详解】(1)解:如图1中,
∵将△CAD绕点C按逆时针方向旋转角α得到△CBE,
∴△ACD≌△BCE,∠DCE=α,
∴CD=CE,
∴∠CDE=.
故答案为:.
(2)解:如图2中,
∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE,
∴△ACD≌△BCE,
∴AD=BE,CD=CE,∠DCE=60°,
∴△CDE是等边三角形,且CF⊥DE,
∴DF=EF=CF,
∵AE=AD+DF+EF,
∴AE=BE+CF.
(3)解:如图,过点D作DF⊥AC于点F,
∵S△ACD=AC DF=DF,
∴当DF取得最大值时,△CAD面积最大,
又∵在△CFD中,DF<CD,
∴只有当CD旋转到与AC垂直时,FD才能取得最大值,即FD=CD=2,
∴△CAD的面积最大,最大面积是2,
故答案为:CD⊥AC;2.
【点睛】本题属于几何变换综合题,考查了等腰三角形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(1)
(2)
(3)存在,最大值为8
【分析】(1)设AC=x,则AB=6-x,表示出△ABC的面积,然后利用二次函数的性质求最大值;
(2)作AG⊥BC于G,利用AAS证明△APG≌△PEH,得PH=AG,再利用含30°角的直角三角形的性质求出AG的长即可;
(3)结合(1)(2)的方法,过点E作EG⊥CA,交CA延长线于G,BH⊥CA,交CA延长线于H,作AD⊥BC于D,首先利用等积法求出BH的长,设CP=x,则AP=6-x,表示出面积,利用二次函数的性质解决问题.
【详解】(1)解:设,则,
,
当时,最大为,
故答案为:;
(2)作于,
将线段绕点顺时针旋转90度,得线段,
,,
,
,
,
,
,
,
,,
,
,
;
(3)的面积存在最大值,理由如下:
过点作,交延长线于,,交延长线于,作于,
由(2)同理知,,
,
,,
,
由勾股定理得,,
,
,
,
在中,,
设,则,
,
的面积为,
当时,的面积最大值为8.
【点睛】本题是三角形综合题,主要考查了旋转的性质,等腰直角三角形的判定与性质,二次函数的性质,全等三角形的判定与性质等知识,构造全等三角形是解题的关键.
同课章节目录
