湘教版九年级下册数学第一章 二次函数 小结与复习 课件(共26张PPT)
文档属性
| 名称 | 湘教版九年级下册数学第一章 二次函数 小结与复习 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第一章 二次函数
小结与复习
湘教版(2024)九年级下册数学课件
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
二次函数
二次函数的概念
二次函数的图象与性质
不共线三点确定二次函数的表达式
二次函数与一元二次方程的联系
二次函数的应用
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
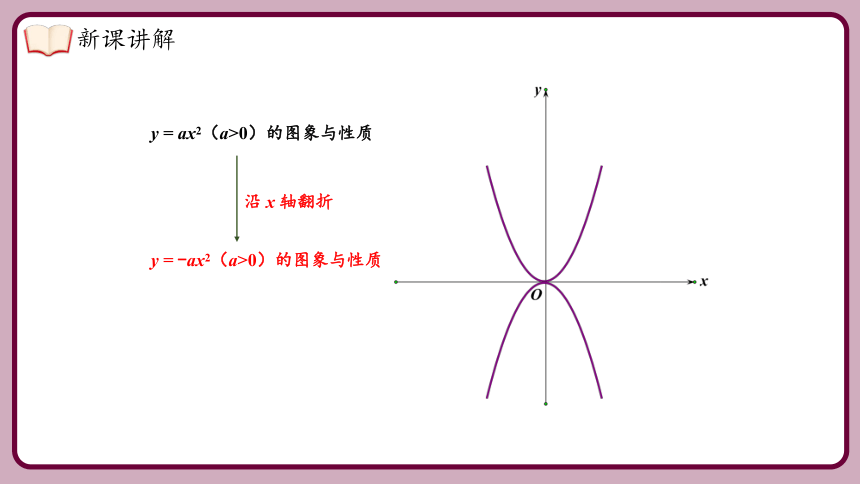
y = ax2(a>0)的图象与性质
沿 x 轴翻折
y = -ax2(a>0)的图象与性质
新课讲解
y = ax2(a>0)的图象与性质
当h < 0时,
向左平移 |h| 个单位
y = a(x - h)2(a>0)的图象与性质
新课讲解
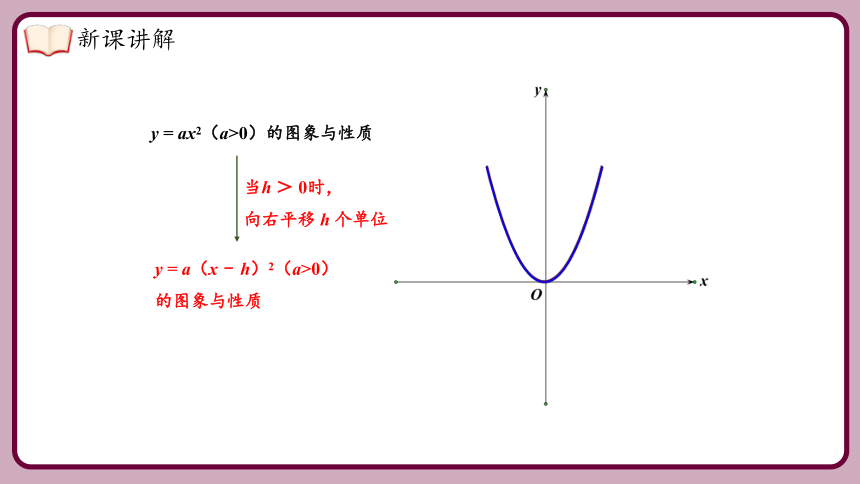
y = ax2(a>0)的图象与性质
当h > 0时,
向右平移 h 个单位
y = a(x - h)2(a>0)的图象与性质
新课讲解
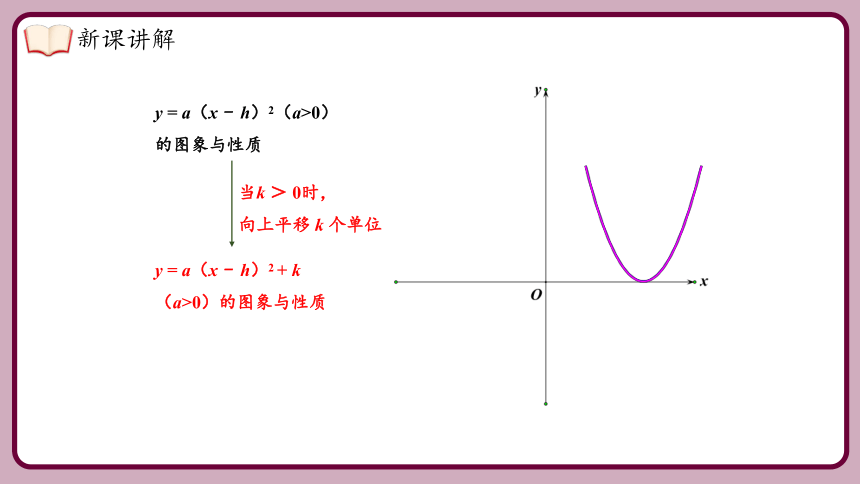
当k > 0时,
向上平移 k 个单位
y = a(x - h)2(a>0)的图象与性质
y = a(x - h)2 + k(a>0)的图象与性质
新课讲解
当k < 0时,
向下平移 |k| 个单位
y = a(x - h)2(a>0)的图象与性质
y = a(x - h)2 + k(a>0)的图象与性质
写成一般形式
y = ax2 + bx + c 的图象与性质
新课讲解
二次函数 y = ax2 + bx + c (a≠0) 中 a,b,c 的变化会引起图象发生哪些变化?
点击播放
新课讲解
课堂练习
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.如图,一张正方形纸板的边长为 4,将它剪去 4 个全等的直角三角形,设这 4 个直角三角形短直角边的长度为 x,四边形ABCD 的面积为 y,求 y 关于 x 的函数表达式.
【教材P37页】
y = 2(x-2)2 + 8 ( 0 < x ≤ 2 )
( 0 < x ≤ 2 )
课堂练习
2. 画出下列二次函数的图象, 并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
课堂练习
2. 画出下列二次函数的图象, 并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
课堂练习
2. 画出下列二次函数的图象, 并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
课堂练习
3. 填空:
(1)抛物线 y = 3x2 先向左平移 2 个单位,得到抛物线_____________; 接着向上平移 1 个单位,得到抛物线__________________.
(2)抛物线 沿着 x 轴翻折并“复制”出来,得到抛物线_______;
接着向右平移 5 个单位, 得到抛物线_______________; 接着向下平移 2 个单位, 得到抛物线__________________ .
y = 3(x+2)2
y = 3(x+2)2+1
【教材P37页】
课堂练习
4. 已知二次函数的图象的顶点坐标为 , 且过点 .
求这个二次函数的表达式及它与 y 轴的交点坐标.
解 设二次函数的表达式为
将点 代入,得
所以,二次函数表达式
与 y 轴交点
【教材P37页】
课堂练习
5. 用配方法求下列二次函数的最大值或最小值.
解
最大值
最小值 -3
【教材P37页】
课堂练习
6. 已知二次函数的图象与 x 轴交于点(2,0) , (-1,0), 与 y 轴
交于点(0,-1). 求这个二次函数的表达式及顶点坐标.
解 设二次函数表达式为
将点(0,-1)代入,得
顶点坐标
【教材P37页】
课堂练习
7. 用图象法求一元二次方程 x2+ 4x - 3 = 0 的根的
近似值(精确到 0.1).
y = x2+ 4x - 3
x1 ≈ -4.6
x2 ≈ 0.6
【教材P37页】
课堂练习
8. 将一个小球以 20m/s 的初速度从地面垂直抛向空中,经过时间
t (s),小球的高度 h(m)为 h = 20t - 5t2 .
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
点击播放
【教材P38页】
课堂练习
8. 将一个小球以 20m/s 的初速度从地面垂直抛向空中,经过时间
t (s),小球的高度 h(m)为 h = 20t - 5t2 .
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
【教材P38页】
解 (1) h = 20t - 5t2 = -5(t-2)2 + 20
当t=2时,h最大,最大值为20
答:经过2s,小球达到最高点,离地面 20 。
(2) h = -5(t-2)2 + 20
令h=0,解得 t=4或t=0(舍去)
答:经过4s,小球落到地上。
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
课堂小结
第一章 二次函数
小结与复习
湘教版(2024)九年级下册数学课件
第一章 二次函数
小结与复习
湘教版(2024)九年级下册数学课件
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
二次函数
二次函数的概念
二次函数的图象与性质
不共线三点确定二次函数的表达式
二次函数与一元二次方程的联系
二次函数的应用
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
y = ax2(a>0)的图象与性质
沿 x 轴翻折
y = -ax2(a>0)的图象与性质
新课讲解
y = ax2(a>0)的图象与性质
当h < 0时,
向左平移 |h| 个单位
y = a(x - h)2(a>0)的图象与性质
新课讲解
y = ax2(a>0)的图象与性质
当h > 0时,
向右平移 h 个单位
y = a(x - h)2(a>0)的图象与性质
新课讲解
当k > 0时,
向上平移 k 个单位
y = a(x - h)2(a>0)的图象与性质
y = a(x - h)2 + k(a>0)的图象与性质
新课讲解
当k < 0时,
向下平移 |k| 个单位
y = a(x - h)2(a>0)的图象与性质
y = a(x - h)2 + k(a>0)的图象与性质
写成一般形式
y = ax2 + bx + c 的图象与性质
新课讲解
二次函数 y = ax2 + bx + c (a≠0) 中 a,b,c 的变化会引起图象发生哪些变化?
点击播放
新课讲解
课堂练习
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.如图,一张正方形纸板的边长为 4,将它剪去 4 个全等的直角三角形,设这 4 个直角三角形短直角边的长度为 x,四边形ABCD 的面积为 y,求 y 关于 x 的函数表达式.
【教材P37页】
y = 2(x-2)2 + 8 ( 0 < x ≤ 2 )
( 0 < x ≤ 2 )
课堂练习
2. 画出下列二次函数的图象, 并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
课堂练习
2. 画出下列二次函数的图象, 并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
课堂练习
2. 画出下列二次函数的图象, 并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
课堂练习
3. 填空:
(1)抛物线 y = 3x2 先向左平移 2 个单位,得到抛物线_____________; 接着向上平移 1 个单位,得到抛物线__________________.
(2)抛物线 沿着 x 轴翻折并“复制”出来,得到抛物线_______;
接着向右平移 5 个单位, 得到抛物线_______________; 接着向下平移 2 个单位, 得到抛物线__________________ .
y = 3(x+2)2
y = 3(x+2)2+1
【教材P37页】
课堂练习
4. 已知二次函数的图象的顶点坐标为 , 且过点 .
求这个二次函数的表达式及它与 y 轴的交点坐标.
解 设二次函数的表达式为
将点 代入,得
所以,二次函数表达式
与 y 轴交点
【教材P37页】
课堂练习
5. 用配方法求下列二次函数的最大值或最小值.
解
最大值
最小值 -3
【教材P37页】
课堂练习
6. 已知二次函数的图象与 x 轴交于点(2,0) , (-1,0), 与 y 轴
交于点(0,-1). 求这个二次函数的表达式及顶点坐标.
解 设二次函数表达式为
将点(0,-1)代入,得
顶点坐标
【教材P37页】
课堂练习
7. 用图象法求一元二次方程 x2+ 4x - 3 = 0 的根的
近似值(精确到 0.1).
y = x2+ 4x - 3
x1 ≈ -4.6
x2 ≈ 0.6
【教材P37页】
课堂练习
8. 将一个小球以 20m/s 的初速度从地面垂直抛向空中,经过时间
t (s),小球的高度 h(m)为 h = 20t - 5t2 .
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
点击播放
【教材P38页】
课堂练习
8. 将一个小球以 20m/s 的初速度从地面垂直抛向空中,经过时间
t (s),小球的高度 h(m)为 h = 20t - 5t2 .
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
【教材P38页】
解 (1) h = 20t - 5t2 = -5(t-2)2 + 20
当t=2时,h最大,最大值为20
答:经过2s,小球达到最高点,离地面 20 。
(2) h = -5(t-2)2 + 20
令h=0,解得 t=4或t=0(舍去)
答:经过4s,小球落到地上。
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
课堂小结
第一章 二次函数
小结与复习
湘教版(2024)九年级下册数学课件
