湘教版九年级下册数学1.3不共线三点确定二次函数的表达式 课件(共22张PPT)
文档属性
| 名称 | 湘教版九年级下册数学1.3不共线三点确定二次函数的表达式 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第一章 二次函数 1.3
不共线三点确定
二次函数的表达式
湘教版(2024)九年级下册数学课件
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
一次函数的表达式是 y = kx + b ,只要求出____和____的值, 就可以确定一次函数的表达式.
二次函数的表达式是 y = ax2 + bx + c (a ≠ 0 ),因此,要确定这个表达式,就需要求出___,___,___的值.
k
b
a
b
c
新课导入
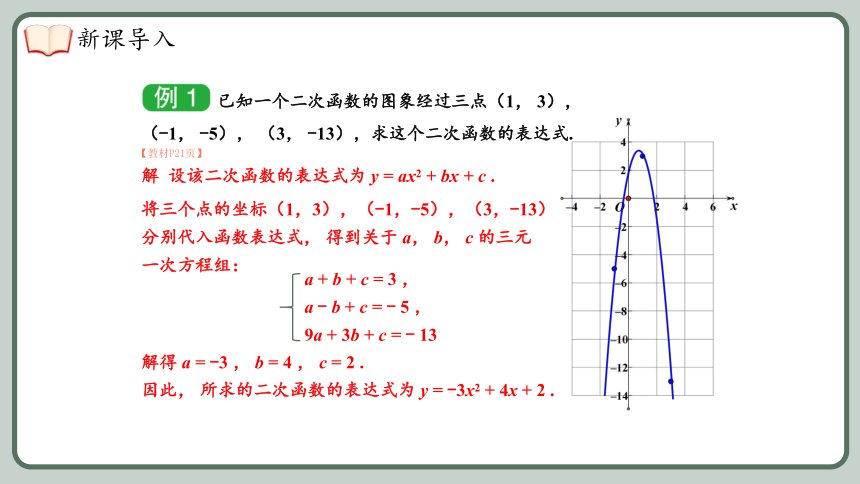
已知一个二次函数的图象经过三点(1, 3), (-1, -5), (3, -13),求这个二次函数的表达式.
解 设该二次函数的表达式为 y = ax2 + bx + c .
将三个点的坐标(1,3),(-1,-5),(3,-13) 分别代入函数表达式, 得到关于 a, b, c 的三元一次方程组:
a + b + c = 3 ,
a - b + c = - 5 ,
9a + 3b + c = - 13
解得 a = -3 , b = 4 , c = 2 .
因此, 所求的二次函数的表达式为 y = -3x2 + 4x + 2 .
【教材P21页】
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
已知三个点的坐标, 是否有一个二次函数, 它的图象经过这三个点?
(1) P(1,-5), Q(-1,3), R(2,-3);
(2) P(1,-5), Q(-1,3), M(2,-9).
解 (1)设有二次函数 y = ax2 + bx + c , 它的图象经过 P, Q, R 三点, 则得到关于 a, b, c 的三元一次方程组:
a+ b + c = -5,
a - b + c = 3 ,
4a + 2b + c = -3,
解得 a = 2 , b = - 4 , c = -3.
因此, 二次函数 y = 2x2 - 4x – 3 的图象经过 P, Q, R 三点.
【教材P21页】
新课讲解
(2) P(1,-5), Q(-1,3), M(2,-9).
解 (2)设有二次函数 y = ax2 + bx + c ,
它的图象经过 P, Q, M 三点,
则得到关于 a, b, c 的三元一次方程组:
a+ b + c = -5,
a - b + c = 3 ,
4a + 2b + c = -9,
解得 a = 0 , b = - 4 , c = -1.
因此, 一次函数 y = - 4x – 1 的图象经过 P, Q, M 三点.
y = - 4x – 1
新课讲解
例2中:两点P(1, -5), Q(-1, 3)确定了一个一次函数 y = - 4x - 1 .
点 R(2, -3)的坐标不适合 y = - 4x - 1 , 因此点 R 不在直线 PQ 上,即P, Q, R 三点不共线.
点 M(2, -9)的坐标适合 y = - 4x - 1,因此点 M在直线 PQ 上,即 P,Q,M 三点共线.
(1) P(1,-5), Q(-1,3), R(2,-3);
(2) P(1,-5), Q(-1,3), M(2,-9).
新课讲解
例2表明: 若给定不共线三点的坐标, 且它们的横坐标两两不等, 则可以确定一个二次函数; 而给定共线三点的坐标, 不能确定二次函数.
(1) P(1,-5), Q(-1,3), R(2,-3);
(2) P(1,-5), Q(-1,3), M(2,-9).
新课讲解
可以证明: 二次函数 y = ax2 + bx + c 的图象上任意三个不同的点都不在一条直线上.
还可以证明: 若给定不共线三点的坐标, 且它们的横坐标两两不等, 则可以确定唯一的一个二次函数, 它的图象经过这三点.
新课讲解
用顶点式求二次函数解析式.
已知二次函数的顶点为A(1,-4)且过B(3,0), 求二次函数解析式.
解:∵抛物线顶点为A(1,-4),
∴设抛物线解析式为 y = a(x-1)2-4,
∵点 B(3,0)在图象上,
∴0 = 4a-4, ∴ a = 1,
∴ y = (x-1)2 - 4,即 y = x2-2x-3.
新课讲解
用交点式求二次函数解析式
已知一抛物线与x轴交于点 A(-2,0),B(1,0),且经过点 C(2,8).求二次函数解析式.
解:A(-2,0),B(1,0)在 x 轴上,设二次函数解析式为 y = a(x+2)(x-1).
又∵图象过点 C(2,8),
∴ 8 = a(2+2)(2-1), ∴a=2,
∴ y = 2(x+2)(x-1)=2x2+2x-4.
新课讲解
已知二次函数 y = ax2+ bx + c 的图象经过三点 A(0,2), B(1,3),C(-1,-1), 求这个二次函数的表达式.
c = 2,
a + b + c = 3 ,
a - b + c = -1,
解 设这个二次函数为 y = ax2 + bx + c
解得 a = -1 , b = 2 , c = 2.
二次函数表达式 y = -x2 + 2x+ 2.
【教材P23页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 若抛物线经过点 (3, 0)和(2, -3), 且以直线 x =1为对称轴,
则该抛物线的表达式为( )
A.y=-x2-2x-3 B.y=x2-2x+3
C.y=x2-2x-3 D.y=-x2+2x-3
C
课堂练习
2. 抛物线 y= ax2+bx+c 与 x 轴的两个交点分别为(-1, 0),
(3, 0),其形状和开口方向与抛物线 y=-2x2 相同,则抛物线
y=ax2+bx+c 的表达式为( )
A.y=-2x2-x+3
B.y=-2x2+4x+5
C.y=-2x2+4x+8
D.y=-2x2+4x+6
D
课堂练习
3.(分类讨论题)已知抛物线过点 A(2,0),B(-1,0),
与 y 轴交于点 C, 且 OC =2, 则这条抛物线的表达式
为( )
A.y=x2-x-2
B.y=-x2+x+2
C.y=x2-x-2 或 y=-x2+x+2
D.y=-x2-x-2 或 y=x2+x+2
C
课堂练习
4. 已知抛物线 y=-x2+bx+c 如图所示, 则此抛物线
的表达式为_________________.
y =-x2+2x+3
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
求二次函数解析式的三种表达式的形式.
(1)已知三点坐标,设二次函数解析式为 y = ax2+bx+c.
(2)已知顶点坐标:设二次函数解析式为 y=a(x-h)2+k.
(3)已知抛物线与 x 轴两交点坐标为(x1,0),(x2,0)可设二次函数解析式为 y = a(x-x1)(x-x2).
课堂小结
第一章 二次函数 1.3
不共线三点确定
二次函数的表达式
湘教版(2024)九年级下册数学课件
第一章 二次函数 1.3
不共线三点确定
二次函数的表达式
湘教版(2024)九年级下册数学课件
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
一次函数的表达式是 y = kx + b ,只要求出____和____的值, 就可以确定一次函数的表达式.
二次函数的表达式是 y = ax2 + bx + c (a ≠ 0 ),因此,要确定这个表达式,就需要求出___,___,___的值.
k
b
a
b
c
新课导入
已知一个二次函数的图象经过三点(1, 3), (-1, -5), (3, -13),求这个二次函数的表达式.
解 设该二次函数的表达式为 y = ax2 + bx + c .
将三个点的坐标(1,3),(-1,-5),(3,-13) 分别代入函数表达式, 得到关于 a, b, c 的三元一次方程组:
a + b + c = 3 ,
a - b + c = - 5 ,
9a + 3b + c = - 13
解得 a = -3 , b = 4 , c = 2 .
因此, 所求的二次函数的表达式为 y = -3x2 + 4x + 2 .
【教材P21页】
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
已知三个点的坐标, 是否有一个二次函数, 它的图象经过这三个点?
(1) P(1,-5), Q(-1,3), R(2,-3);
(2) P(1,-5), Q(-1,3), M(2,-9).
解 (1)设有二次函数 y = ax2 + bx + c , 它的图象经过 P, Q, R 三点, 则得到关于 a, b, c 的三元一次方程组:
a+ b + c = -5,
a - b + c = 3 ,
4a + 2b + c = -3,
解得 a = 2 , b = - 4 , c = -3.
因此, 二次函数 y = 2x2 - 4x – 3 的图象经过 P, Q, R 三点.
【教材P21页】
新课讲解
(2) P(1,-5), Q(-1,3), M(2,-9).
解 (2)设有二次函数 y = ax2 + bx + c ,
它的图象经过 P, Q, M 三点,
则得到关于 a, b, c 的三元一次方程组:
a+ b + c = -5,
a - b + c = 3 ,
4a + 2b + c = -9,
解得 a = 0 , b = - 4 , c = -1.
因此, 一次函数 y = - 4x – 1 的图象经过 P, Q, M 三点.
y = - 4x – 1
新课讲解
例2中:两点P(1, -5), Q(-1, 3)确定了一个一次函数 y = - 4x - 1 .
点 R(2, -3)的坐标不适合 y = - 4x - 1 , 因此点 R 不在直线 PQ 上,即P, Q, R 三点不共线.
点 M(2, -9)的坐标适合 y = - 4x - 1,因此点 M在直线 PQ 上,即 P,Q,M 三点共线.
(1) P(1,-5), Q(-1,3), R(2,-3);
(2) P(1,-5), Q(-1,3), M(2,-9).
新课讲解
例2表明: 若给定不共线三点的坐标, 且它们的横坐标两两不等, 则可以确定一个二次函数; 而给定共线三点的坐标, 不能确定二次函数.
(1) P(1,-5), Q(-1,3), R(2,-3);
(2) P(1,-5), Q(-1,3), M(2,-9).
新课讲解
可以证明: 二次函数 y = ax2 + bx + c 的图象上任意三个不同的点都不在一条直线上.
还可以证明: 若给定不共线三点的坐标, 且它们的横坐标两两不等, 则可以确定唯一的一个二次函数, 它的图象经过这三点.
新课讲解
用顶点式求二次函数解析式.
已知二次函数的顶点为A(1,-4)且过B(3,0), 求二次函数解析式.
解:∵抛物线顶点为A(1,-4),
∴设抛物线解析式为 y = a(x-1)2-4,
∵点 B(3,0)在图象上,
∴0 = 4a-4, ∴ a = 1,
∴ y = (x-1)2 - 4,即 y = x2-2x-3.
新课讲解
用交点式求二次函数解析式
已知一抛物线与x轴交于点 A(-2,0),B(1,0),且经过点 C(2,8).求二次函数解析式.
解:A(-2,0),B(1,0)在 x 轴上,设二次函数解析式为 y = a(x+2)(x-1).
又∵图象过点 C(2,8),
∴ 8 = a(2+2)(2-1), ∴a=2,
∴ y = 2(x+2)(x-1)=2x2+2x-4.
新课讲解
已知二次函数 y = ax2+ bx + c 的图象经过三点 A(0,2), B(1,3),C(-1,-1), 求这个二次函数的表达式.
c = 2,
a + b + c = 3 ,
a - b + c = -1,
解 设这个二次函数为 y = ax2 + bx + c
解得 a = -1 , b = 2 , c = 2.
二次函数表达式 y = -x2 + 2x+ 2.
【教材P23页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 若抛物线经过点 (3, 0)和(2, -3), 且以直线 x =1为对称轴,
则该抛物线的表达式为( )
A.y=-x2-2x-3 B.y=x2-2x+3
C.y=x2-2x-3 D.y=-x2+2x-3
C
课堂练习
2. 抛物线 y= ax2+bx+c 与 x 轴的两个交点分别为(-1, 0),
(3, 0),其形状和开口方向与抛物线 y=-2x2 相同,则抛物线
y=ax2+bx+c 的表达式为( )
A.y=-2x2-x+3
B.y=-2x2+4x+5
C.y=-2x2+4x+8
D.y=-2x2+4x+6
D
课堂练习
3.(分类讨论题)已知抛物线过点 A(2,0),B(-1,0),
与 y 轴交于点 C, 且 OC =2, 则这条抛物线的表达式
为( )
A.y=x2-x-2
B.y=-x2+x+2
C.y=x2-x-2 或 y=-x2+x+2
D.y=-x2-x-2 或 y=x2+x+2
C
课堂练习
4. 已知抛物线 y=-x2+bx+c 如图所示, 则此抛物线
的表达式为_________________.
y =-x2+2x+3
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
求二次函数解析式的三种表达式的形式.
(1)已知三点坐标,设二次函数解析式为 y = ax2+bx+c.
(2)已知顶点坐标:设二次函数解析式为 y=a(x-h)2+k.
(3)已知抛物线与 x 轴两交点坐标为(x1,0),(x2,0)可设二次函数解析式为 y = a(x-x1)(x-x2).
课堂小结
第一章 二次函数 1.3
不共线三点确定
二次函数的表达式
湘教版(2024)九年级下册数学课件
