5.1.2 数列中的递推 课件(18页)
文档属性
| 名称 | 5.1.2 数列中的递推 课件(18页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 646.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览






文档简介
5.1.2 数列中的递推
第五章 数列
1.了解递推公式是给出数列的一种方法.
2.理解递推公式的含义,能够根据递推公式写出数列的前n项.
3.掌握由数列的前n项和求数列的通项公式的方法.
问题:如图,某会议室有若干排座位,每一排的座位数构成的数列设为{an}.从第二排起,后一排都比前一排多2个座位.
(1)第n排与第n-1排座位有什么关系?
(2)若第一排有7个座位,数列{an}是怎样的一列数?
(1)an=an-1+2(n∈N+且n≥2)
(2)7,9,11,13,15,…
一、数列的递推关系
如果已知数列的首项(或前几项),且数列的相邻两项或两项以上的关系都可以用一个公式来表示,则称这个公式为数列的递推关系(也称为递推公式或递归公式).
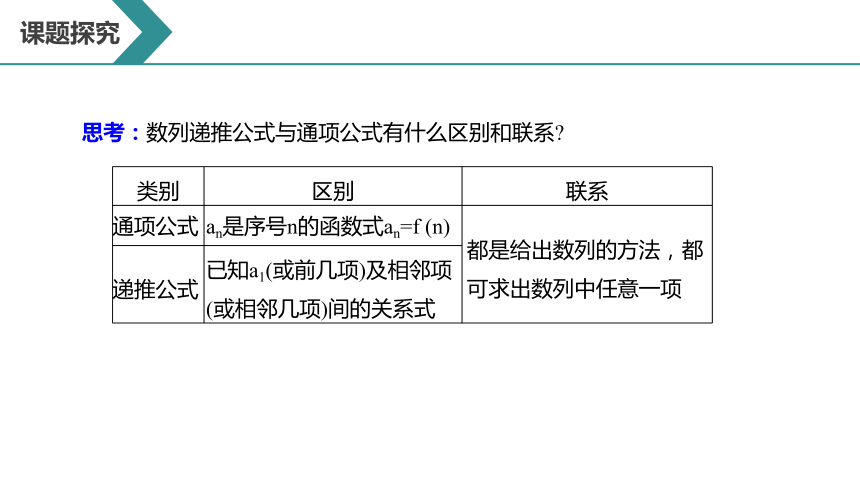
思考:数列递推公式与通项公式有什么区别和联系?
{5940675A-B579-460E-94D1-54222C63F5DA} 类别
区别
联系
通项公式
an是序号n的函数式an=f (n)
都是给出数列的方法,都可求出数列中任意一项
递推公式
已知a1(或前几项)及相邻项(或相邻几项)间的关系式
例1 数列12, 14, 18, 116,…的递推关系可以是( )
?
A. ????????=12????+1(?????∈????+?) B. ????????=12????(?????∈????+?)
C. ????????+1=12????????(?????∈????+?) D. ????????+1=2????????(?????∈????+?)
?
解析:观察数列,发现 ????2????1=????3????2=????4????3=12,
即从数列第二项起,后一项除以前一项的值都为12,
所以递推关系为????????+1=12????????(?????∈????+?)
?
C
例2 已知数列{????????}的第1项????1=1,以后的各项由公式????????+1=2????????????????+2给出,试写出这个数列的前5项.
?
解:因为????1=1,????????+1=2????????????????+2,所以 ????2=2????1????1+2=23, ????3=2????2????2+2=2×2323+2=12,
?
????4=2????3????3+2=2×1212+2=25, ????5=2????4????4+2=2×2525+2=13.
?
故该数列的前5项为1,23,12,25,13.
?
应用数列的递推关系求数列的项的方法
①如果项的序号较小,一般直接代入递推关系,利用顺推或倒推递进行求解;
②如果项的序号较大,一般先根据递推关系写出数列的前几项,进而发现数列的周期或其他规律,然后利用周期性或其他规律求项.
归纳总结
讨论:已知某电子书,今年上半年每个月的销售量构成数列
220,530,950,1360,1820,2350.
假设你是该电子书的销售人员,关于上述数列除了每一个数字的大小和增长趋势外,你还会关心什么?
作为销售人员,一般来说还会关心上半年电子书的总销售量,即
220+530+950+1360+1820+2350=7230.
二、数列的前n项和
一般地,给定数列{an},称
Sn=a1+a2+a3+…+an
为数列{an}的前n项和.
例如,对于探究中的数列来说,
S1=a1=220,
S2=a1+a2=220+530=750,
S3=a1+a2+a3=S2+a3=750+1360=2110,等等.
问题:已知数列{an}的前????项和为Sn=2?????+1,你能写出a1,a2,a3吗?
?
∵????1=2×1+1=3,又∵????1=????1,∴????1=3.
∵ ????2=2×2+1=5,又∵????2=????1+????2, ∴????2=S2?????1=5?3=2.
∵ ????3=2×3+1=7,又∵????3=????1+????2+????3=????2+????3, ∴????3=????3?S2=7-5=2.
?
追问:你发现规律了吗?如何来求????????呢?
?
三、 an与Sn的关系
一般的如果数列{an}的前????项和为Sn,那么当????≥2有,
Sn-1=a1+a2+a3+…+an-1
Sn=a1+a2+a3+…+an
所以Sn=Sn-1+an
因此
?
例3 设Sn为数列{an}的前n项和,Sn=2n2-30n.求a1及an.
解:因为Sn=2n2-30n,所以当n=1时,a1=S1=2×12-30×1=-28,
当n≥2时,an=Sn-Sn-1=2n2-30n-[2(n-1)2-30(n-1)]=4n-32.
验证当n=1时上式成立,
所以an=4n-32,n∈N+.
变式:设Sn为数列{an}的前n项和,Sn=2n2-30n+1,求an.
解:因为Sn=2n2-30n+1,所以当n=1时,a1=S1=2×12-30×1+1=-27,
当n≥2时,an=Sn-Sn-1=2n2-30n+1-[2(n-1)2-30(n-1)+1]=4n-32.
当n=1时,a1=-27不符合上式.
所以an=?27,n=1,??????????4n?32,n≥2.
?
已知前????项和????????求通项公式????????的步骤
?
(1)当????=1时,????1=????1;
(2)当????≥2时,根据????????写出?????????1,化简????????=??????????????????1;
(3)如果????1满足通项公式????????=??????????????????1,那么数列{????????}的通项公式为????????=??????????????????1;如果????1不满足通项公式????????=??????????????????1,那么数列{????????}的通项公式要分段表示为????????=????1,????=1,&??????????????????1,????≥2.
?
方法归纳
1. 数列的递推公式是什么?它与通项公式有什么区别联系?
2. 怎样求数列的前 n 项和公式?如何利用该公式求数列的通项公式?
结合本节课所学,回答下列问题?
1.已知数列{an}满足a1=12,anan-1=an+an-1,则这个数列的第5项是( )
A.1 B.12
C.34 D.58
2.观察下列各式:
a+b=1,????2+????2=3 ,????3+????3=4 ,????4+????4=7 ,????5+????5=11 ,…,
则????10+????10=_________.
?
B
123
3.数列{an}的构成法则如下:a1=1,如果an-2为自然数且之前未出现过,则用递推公式an+1=an-2,否则用递推公式an+1=3an,则a6= .?
15
第五章 数列
1.了解递推公式是给出数列的一种方法.
2.理解递推公式的含义,能够根据递推公式写出数列的前n项.
3.掌握由数列的前n项和求数列的通项公式的方法.
问题:如图,某会议室有若干排座位,每一排的座位数构成的数列设为{an}.从第二排起,后一排都比前一排多2个座位.
(1)第n排与第n-1排座位有什么关系?
(2)若第一排有7个座位,数列{an}是怎样的一列数?
(1)an=an-1+2(n∈N+且n≥2)
(2)7,9,11,13,15,…
一、数列的递推关系
如果已知数列的首项(或前几项),且数列的相邻两项或两项以上的关系都可以用一个公式来表示,则称这个公式为数列的递推关系(也称为递推公式或递归公式).
思考:数列递推公式与通项公式有什么区别和联系?
{5940675A-B579-460E-94D1-54222C63F5DA} 类别
区别
联系
通项公式
an是序号n的函数式an=f (n)
都是给出数列的方法,都可求出数列中任意一项
递推公式
已知a1(或前几项)及相邻项(或相邻几项)间的关系式
例1 数列12, 14, 18, 116,…的递推关系可以是( )
?
A. ????????=12????+1(?????∈????+?) B. ????????=12????(?????∈????+?)
C. ????????+1=12????????(?????∈????+?) D. ????????+1=2????????(?????∈????+?)
?
解析:观察数列,发现 ????2????1=????3????2=????4????3=12,
即从数列第二项起,后一项除以前一项的值都为12,
所以递推关系为????????+1=12????????(?????∈????+?)
?
C
例2 已知数列{????????}的第1项????1=1,以后的各项由公式????????+1=2????????????????+2给出,试写出这个数列的前5项.
?
解:因为????1=1,????????+1=2????????????????+2,所以 ????2=2????1????1+2=23, ????3=2????2????2+2=2×2323+2=12,
?
????4=2????3????3+2=2×1212+2=25, ????5=2????4????4+2=2×2525+2=13.
?
故该数列的前5项为1,23,12,25,13.
?
应用数列的递推关系求数列的项的方法
①如果项的序号较小,一般直接代入递推关系,利用顺推或倒推递进行求解;
②如果项的序号较大,一般先根据递推关系写出数列的前几项,进而发现数列的周期或其他规律,然后利用周期性或其他规律求项.
归纳总结
讨论:已知某电子书,今年上半年每个月的销售量构成数列
220,530,950,1360,1820,2350.
假设你是该电子书的销售人员,关于上述数列除了每一个数字的大小和增长趋势外,你还会关心什么?
作为销售人员,一般来说还会关心上半年电子书的总销售量,即
220+530+950+1360+1820+2350=7230.
二、数列的前n项和
一般地,给定数列{an},称
Sn=a1+a2+a3+…+an
为数列{an}的前n项和.
例如,对于探究中的数列来说,
S1=a1=220,
S2=a1+a2=220+530=750,
S3=a1+a2+a3=S2+a3=750+1360=2110,等等.
问题:已知数列{an}的前????项和为Sn=2?????+1,你能写出a1,a2,a3吗?
?
∵????1=2×1+1=3,又∵????1=????1,∴????1=3.
∵ ????2=2×2+1=5,又∵????2=????1+????2, ∴????2=S2?????1=5?3=2.
∵ ????3=2×3+1=7,又∵????3=????1+????2+????3=????2+????3, ∴????3=????3?S2=7-5=2.
?
追问:你发现规律了吗?如何来求????????呢?
?
三、 an与Sn的关系
一般的如果数列{an}的前????项和为Sn,那么当????≥2有,
Sn-1=a1+a2+a3+…+an-1
Sn=a1+a2+a3+…+an
所以Sn=Sn-1+an
因此
?
例3 设Sn为数列{an}的前n项和,Sn=2n2-30n.求a1及an.
解:因为Sn=2n2-30n,所以当n=1时,a1=S1=2×12-30×1=-28,
当n≥2时,an=Sn-Sn-1=2n2-30n-[2(n-1)2-30(n-1)]=4n-32.
验证当n=1时上式成立,
所以an=4n-32,n∈N+.
变式:设Sn为数列{an}的前n项和,Sn=2n2-30n+1,求an.
解:因为Sn=2n2-30n+1,所以当n=1时,a1=S1=2×12-30×1+1=-27,
当n≥2时,an=Sn-Sn-1=2n2-30n+1-[2(n-1)2-30(n-1)+1]=4n-32.
当n=1时,a1=-27不符合上式.
所以an=?27,n=1,??????????4n?32,n≥2.
?
已知前????项和????????求通项公式????????的步骤
?
(1)当????=1时,????1=????1;
(2)当????≥2时,根据????????写出?????????1,化简????????=??????????????????1;
(3)如果????1满足通项公式????????=??????????????????1,那么数列{????????}的通项公式为????????=??????????????????1;如果????1不满足通项公式????????=??????????????????1,那么数列{????????}的通项公式要分段表示为????????=????1,????=1,&??????????????????1,????≥2.
?
方法归纳
1. 数列的递推公式是什么?它与通项公式有什么区别联系?
2. 怎样求数列的前 n 项和公式?如何利用该公式求数列的通项公式?
结合本节课所学,回答下列问题?
1.已知数列{an}满足a1=12,anan-1=an+an-1,则这个数列的第5项是( )
A.1 B.12
C.34 D.58
2.观察下列各式:
a+b=1,????2+????2=3 ,????3+????3=4 ,????4+????4=7 ,????5+????5=11 ,…,
则????10+????10=_________.
?
B
123
3.数列{an}的构成法则如下:a1=1,如果an-2为自然数且之前未出现过,则用递推公式an+1=an-2,否则用递推公式an+1=3an,则a6= .?
15
