5.2.1 等差数列 课件(共35张PPT) 2024-2025学年高二数学人教B版(2019)选择性必修第三册
文档属性
| 名称 | 5.2.1 等差数列 课件(共35张PPT) 2024-2025学年高二数学人教B版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 22:00:57 | ||
图片预览











文档简介
(共35张PPT)
5.2.1 等差数列
第五章 数列
5.2.1 课时1
等差数列的定义
第五章 数列
1.理解等差数列的概念.
2.掌握等差数列的通项公式及运用.
3.会判断一个数列是否为等差数列.
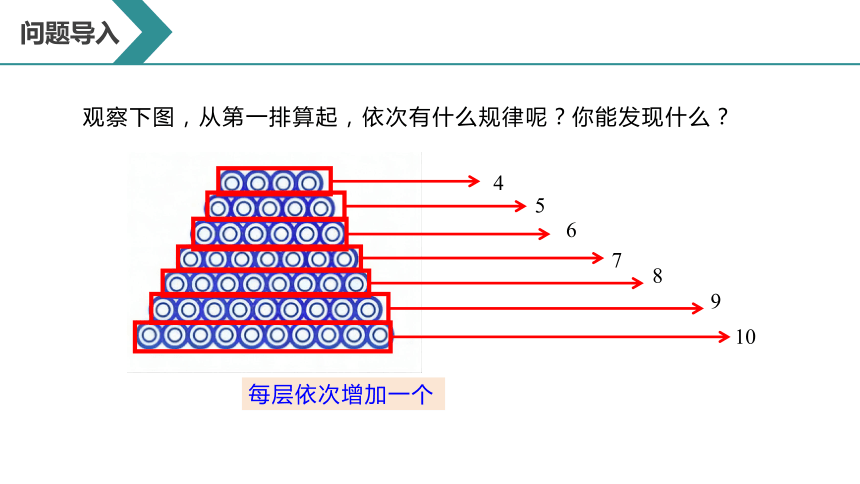
观察下图,从第一排算起,依次有什么规律呢?你能发现什么?
4
5
6
7
8
9
10
每层依次增加一个
观察上述几组数列,你能发现什么共同特点:
(1)1,2,3,4,5...
(2)3000,3500,4000,4500...
(3)250,245,240,235,230...
d=1
d=500
d=-5
共同特点:从第2项起,每一项与前一项的差都等于同一常数.
对于一个数列,如果从第 2 项起,每一项与它的前一项的差都是同一个常数 ,那么称这样的数列为等差数列,称这个常数为等差数列的公差,通常用字母d表示.
等差数列{an}中,a2-a1=a3-a2=…=an-an-1=…= d ,d∈R.
概念讲解
练习:判断下列数列是否是等差数列,如果是,写出它的公差.
(1)1,1.1,1.11,1.111,1.1111,1.11111;
(2)-1,-3,-5,-7;
(3)1,2,4,6,8,10;
(4)7,7,7,7,7;
(5)
不是,公差不是同一个常数
不是,数列从第2项起差不是同一常数
是,公差
是,公差
分析:要确定一个数列是不是等差数列,可根据定义 进行判断,或其变形式,进行判断.
是,公差
归纳总结
一个数列从第2项起,每一项与它前一项的差即使等于常数,这个数列也不一定是等差数列,因为当这些常数不同时,该数列不是等差数列,因此定义中强调“同一个常数”,即该常数与n无关.
数列{an}是等差数列 an - an -1= d (n≥2,且n ∈ N*)
讨论:已知等差数列{an}的首项为a1,公差为d,如何求得它的通项公式
由等差数列的定义可知,an-an-1=d(n≥2),
思路一:an=an-1+d,
故有a2=a1+d,a3=a2+d=a1+2d,a4=a3+d=a1+3d,…
归纳可得,an=a1+(n-1)d(n≥2).
思路二:a2-a1=d,a3-a2=d,a4-a3=d,…an-an-1=d,
左右两边分别相加可得,an-a1=(n-1)d,即an=a1+(n-1)d(n≥2).
若一个等差数列{an},首项是a1,公差是d,则其通项公式为an=a1+(n-1)d.
概念讲解
可以看成是an关于n的一次函数
等差数列的通项公式是关于三个基本量a1,d和n的表达式,所以由首项a1和公差d可以求出数列中的任意一项.
注意:
(1)等差数列的通项公式是关于三个基本量a1,d,n的表达式,所以由首项a1和公差d可以求出数列中的任意一项.
(2)等差数列的通项公式可以推广为an=am+(n-m)d,它阐明了等差数列中任意两项的关系;也可以变形为d= ,知道等差数列中任意两项,可以求公差d.
例1 若数列{an}是等差数列,a15=8,a60=20,求an.
解:设等差数列{an}的公差为d,
例2 在等差数列{an}中,
(1)若a5=15,a17=39,试判断91是否为此数列中的项;
(2)若a2=11,a8=5,求a10.
∴an=7+2(n-1)=2n+5.
令2n+5=91,得n=43.
∵43为正整数,∴91是此数列中的项.
(2)若a2=11,a8=5,求a10.
∴an=12+(n-1)×(-1)=13-n,
∴a10=13-10=3.
方法总结
1.等差数列的通项公式可由首项与公差确定,所以要求等差数列的通项公式,只需求出首项与公差.
2.等差数列{an}的通项公式an=a1+(n-1)d中共含有四个参数,即a1,d,n,an,如果知道了其中的任意三个数,那么就可以由通项公式求出第四个数,这一求未知量的过程,我们通常称之为“知三求一”.
3.通项公式可变形为an=dn+(a1-d),可把an看作自变量为n的一次函数.
等差数列通项公式的求法与应用技巧
从函数角度研究等差数列{an}
若首项是a1,公差是d,则等差数列{an}的通项公式为an=a1+(n-1)d.就通项公式而言,确定一个数列的每一项的要素是首项a1和公差d,因此,二者可以视为常数,项数n是自变量,项an是函数值.
对于an=a1+(n-1)d=dn+(a1-d),可将an记作f(n),它是定义在正整数集(或其子集)上的函数.其图象是直线y=dx+(a1-d)上的一些等间隔的点,这些点的横坐标是正整数,其中公差d是该直线的斜率,即自变量每增加1,函数值增加d.
1
2
3
4
O
n
an
1
2
3
4
O
n
an
a1-d
1
2
3
4
O
n
an
a1
d>0
d<0
d=0
数列{an}为递增数列
数列{an}为递减数列
数列{an}为常数列
例3 设{an}是等差数列,则“a1A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:由题意可得公差d=a2-a1=a3-a2>0,
所以数列{an}是递增数列,即充分性成立;
若数列{an}是递增数列,则必有a1C
1.(多选)下列数列是等差数列的是( )
A.1,1,1,1,1 B.4,7,10,13,16
C. D.-3,-2,-1,1,2
2.已知等差数列的前三项依次为a-1,a+1,2a+3,则此数列的第n项为( )
A.2n-5 B.2n-3 C.2n-1 D.2n+1
ABC
B
3.在等差数列{an}中,a2=-5,a6=a4+6,则a1等于( )
A.-9 B.-8 C.-7 D.-4
4.等差数列{an}:-3,-7,-11,…的一个通项公式为an=________.
B
11
5.2.1 课时2
等差数列的性质
第五章 数列
1.掌握等差中项的概念,会求等差中项.
2.掌握等差数列的有关性质,并能灵活运用性质简化运算,解决简单的数列问题.
观察发现:某种卷筒卫生纸绕在盘上,空盘时盘芯直径为
上面这个数列,其任意连续三项之间有什么样的关系?
前一项与后一项的和是中间项的2倍.
如果在a与b之间插入一个数A,使a,A,b成等差数列,那么A叫作a与b的等差中项.A=.
概念讲解
例1 若m和2n的等差中项为4,2m和n的等差中项为5,求m和n的等差中项.
解:由m和2n的等差中项为4,得m+2n=8.
又由2m和n的等差中项为5,得2m+n=10.
两式相加,得3m+3n=18,即m+n=6.
所以m和n的等差中项为=3.
思考:对于等差数列{an},首项为a1,公差为d,回答下列问题:
(1)a10+a20与a14+a16是什么关系
(2)a6,a10,a14成等差数列吗
(3)2am=am-1+am+1(m∈N+,m>1)是否恒成立
(1)相等.
(2)成等差数列.
(3)是.
等差数列的项与序号的性质
①两项关系
通项公式的推广:an=am+(n-m)d (m,n∈N+).
②多项关系
项的运算性质:若m+n=p+q(m,n,p,q∈N+),则am+an=ap+aq.
特别地,若m+n=2p(m,n,p∈N+),则am+an=2ap .
归纳总结
例2 在等差数列{an}中,已知a2=5,a8=17,求数列的公差及通项公式.
解:设等差数列{an}的公差为d.
因为a8=a2+(8-2)d,所以17=5+6d,解得d=2.
又因为an=a2+(n-2)d,所以an=5+(n-2)×2=2n+1,n∈N+.
灵活利用等差数列的性质,可以减少运算.令m=1,an=am+(n-m)d即变为an=a1+(n-1)d,可以减少记忆负担.
例3 在公差为d的等差数列{an}中,
(1)已知a2+a3+a23+a24=48,求a13;
(2)已知a2+a3+a4+a5=34,a2·a5=52,求d.
解:(1)根据已知条件a2+a3+a23+a24=48及a2+a24=a3+a23=2a13,
得4a13=48,
∴a13=12.
(2)已知a2+a3+a4+a5=34,a2·a5=52,求d.
(2)由a2+a3+a4+a5=34及a3+a4=a2+a5得2(a2+a5)=34,
即a2+a5=17.
例4 一个木制梯架的上、下两底边分别为33 cm,75cm,把梯形的两腰各6等分,用平行木条连接各对应分点,构成梯形架的各级.试计算梯形架间各级的宽度.
解:记梯形架自上而下各级宽度所构成的数列为{an},则由梯形中位线的性质,易知相邻三项均成等差数列,即数列{an}成等差数列.
依题意,有a1=33cm,a7=75cm,
现要求a2,a3,a4,a5,a6,即中间5级的宽度.由等差数列的定义,有
所以a2=33+7=40(cm),a3=40+7=47(cm),a4=47+7=54(cm),a5=54+7=61(cm),a6=61+7=68(cm).
因此梯形架中间各级的宽度自上而下依次是40cm,47cm,54cm,61cm,68cm.
例4 一个木制梯架的上、下两底边分别为33 cm,75cm,把梯形的两腰各6等分,用平行木条连接各对应分点,构成梯形架的各级.试计算梯形架间各级的宽度.
根据今天所学,回答下列问题:
1.什么是等差中项,怎样求等差中项?
2.等差数列的性质有哪些?
3.如何利用等差数列解决实际问题?
1.已知{an}为等差数列,a4+a7+a10=30,则a3-2a5的值为( )
A.10 B.-10 C.15 D.-15
2.等差数列20,17,14,11,…中第一个负数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
3.在等差数列{an}中,已知a4+a8=16,则a2+a10=________.
4.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )
A.1升 B.升 C.升 D.升
D
B
B
16
5.2.1 等差数列
第五章 数列
5.2.1 课时1
等差数列的定义
第五章 数列
1.理解等差数列的概念.
2.掌握等差数列的通项公式及运用.
3.会判断一个数列是否为等差数列.
观察下图,从第一排算起,依次有什么规律呢?你能发现什么?
4
5
6
7
8
9
10
每层依次增加一个
观察上述几组数列,你能发现什么共同特点:
(1)1,2,3,4,5...
(2)3000,3500,4000,4500...
(3)250,245,240,235,230...
d=1
d=500
d=-5
共同特点:从第2项起,每一项与前一项的差都等于同一常数.
对于一个数列,如果从第 2 项起,每一项与它的前一项的差都是同一个常数 ,那么称这样的数列为等差数列,称这个常数为等差数列的公差,通常用字母d表示.
等差数列{an}中,a2-a1=a3-a2=…=an-an-1=…= d ,d∈R.
概念讲解
练习:判断下列数列是否是等差数列,如果是,写出它的公差.
(1)1,1.1,1.11,1.111,1.1111,1.11111;
(2)-1,-3,-5,-7;
(3)1,2,4,6,8,10;
(4)7,7,7,7,7;
(5)
不是,公差不是同一个常数
不是,数列从第2项起差不是同一常数
是,公差
是,公差
分析:要确定一个数列是不是等差数列,可根据定义 进行判断,或其变形式,进行判断.
是,公差
归纳总结
一个数列从第2项起,每一项与它前一项的差即使等于常数,这个数列也不一定是等差数列,因为当这些常数不同时,该数列不是等差数列,因此定义中强调“同一个常数”,即该常数与n无关.
数列{an}是等差数列 an - an -1= d (n≥2,且n ∈ N*)
讨论:已知等差数列{an}的首项为a1,公差为d,如何求得它的通项公式
由等差数列的定义可知,an-an-1=d(n≥2),
思路一:an=an-1+d,
故有a2=a1+d,a3=a2+d=a1+2d,a4=a3+d=a1+3d,…
归纳可得,an=a1+(n-1)d(n≥2).
思路二:a2-a1=d,a3-a2=d,a4-a3=d,…an-an-1=d,
左右两边分别相加可得,an-a1=(n-1)d,即an=a1+(n-1)d(n≥2).
若一个等差数列{an},首项是a1,公差是d,则其通项公式为an=a1+(n-1)d.
概念讲解
可以看成是an关于n的一次函数
等差数列的通项公式是关于三个基本量a1,d和n的表达式,所以由首项a1和公差d可以求出数列中的任意一项.
注意:
(1)等差数列的通项公式是关于三个基本量a1,d,n的表达式,所以由首项a1和公差d可以求出数列中的任意一项.
(2)等差数列的通项公式可以推广为an=am+(n-m)d,它阐明了等差数列中任意两项的关系;也可以变形为d= ,知道等差数列中任意两项,可以求公差d.
例1 若数列{an}是等差数列,a15=8,a60=20,求an.
解:设等差数列{an}的公差为d,
例2 在等差数列{an}中,
(1)若a5=15,a17=39,试判断91是否为此数列中的项;
(2)若a2=11,a8=5,求a10.
∴an=7+2(n-1)=2n+5.
令2n+5=91,得n=43.
∵43为正整数,∴91是此数列中的项.
(2)若a2=11,a8=5,求a10.
∴an=12+(n-1)×(-1)=13-n,
∴a10=13-10=3.
方法总结
1.等差数列的通项公式可由首项与公差确定,所以要求等差数列的通项公式,只需求出首项与公差.
2.等差数列{an}的通项公式an=a1+(n-1)d中共含有四个参数,即a1,d,n,an,如果知道了其中的任意三个数,那么就可以由通项公式求出第四个数,这一求未知量的过程,我们通常称之为“知三求一”.
3.通项公式可变形为an=dn+(a1-d),可把an看作自变量为n的一次函数.
等差数列通项公式的求法与应用技巧
从函数角度研究等差数列{an}
若首项是a1,公差是d,则等差数列{an}的通项公式为an=a1+(n-1)d.就通项公式而言,确定一个数列的每一项的要素是首项a1和公差d,因此,二者可以视为常数,项数n是自变量,项an是函数值.
对于an=a1+(n-1)d=dn+(a1-d),可将an记作f(n),它是定义在正整数集(或其子集)上的函数.其图象是直线y=dx+(a1-d)上的一些等间隔的点,这些点的横坐标是正整数,其中公差d是该直线的斜率,即自变量每增加1,函数值增加d.
1
2
3
4
O
n
an
1
2
3
4
O
n
an
a1-d
1
2
3
4
O
n
an
a1
d>0
d<0
d=0
数列{an}为递增数列
数列{an}为递减数列
数列{an}为常数列
例3 设{an}是等差数列,则“a1
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:由题意可得公差d=a2-a1=a3-a2>0,
所以数列{an}是递增数列,即充分性成立;
若数列{an}是递增数列,则必有a1
1.(多选)下列数列是等差数列的是( )
A.1,1,1,1,1 B.4,7,10,13,16
C. D.-3,-2,-1,1,2
2.已知等差数列的前三项依次为a-1,a+1,2a+3,则此数列的第n项为( )
A.2n-5 B.2n-3 C.2n-1 D.2n+1
ABC
B
3.在等差数列{an}中,a2=-5,a6=a4+6,则a1等于( )
A.-9 B.-8 C.-7 D.-4
4.等差数列{an}:-3,-7,-11,…的一个通项公式为an=________.
B
11
5.2.1 课时2
等差数列的性质
第五章 数列
1.掌握等差中项的概念,会求等差中项.
2.掌握等差数列的有关性质,并能灵活运用性质简化运算,解决简单的数列问题.
观察发现:某种卷筒卫生纸绕在盘上,空盘时盘芯直径为
上面这个数列,其任意连续三项之间有什么样的关系?
前一项与后一项的和是中间项的2倍.
如果在a与b之间插入一个数A,使a,A,b成等差数列,那么A叫作a与b的等差中项.A=.
概念讲解
例1 若m和2n的等差中项为4,2m和n的等差中项为5,求m和n的等差中项.
解:由m和2n的等差中项为4,得m+2n=8.
又由2m和n的等差中项为5,得2m+n=10.
两式相加,得3m+3n=18,即m+n=6.
所以m和n的等差中项为=3.
思考:对于等差数列{an},首项为a1,公差为d,回答下列问题:
(1)a10+a20与a14+a16是什么关系
(2)a6,a10,a14成等差数列吗
(3)2am=am-1+am+1(m∈N+,m>1)是否恒成立
(1)相等.
(2)成等差数列.
(3)是.
等差数列的项与序号的性质
①两项关系
通项公式的推广:an=am+(n-m)d (m,n∈N+).
②多项关系
项的运算性质:若m+n=p+q(m,n,p,q∈N+),则am+an=ap+aq.
特别地,若m+n=2p(m,n,p∈N+),则am+an=2ap .
归纳总结
例2 在等差数列{an}中,已知a2=5,a8=17,求数列的公差及通项公式.
解:设等差数列{an}的公差为d.
因为a8=a2+(8-2)d,所以17=5+6d,解得d=2.
又因为an=a2+(n-2)d,所以an=5+(n-2)×2=2n+1,n∈N+.
灵活利用等差数列的性质,可以减少运算.令m=1,an=am+(n-m)d即变为an=a1+(n-1)d,可以减少记忆负担.
例3 在公差为d的等差数列{an}中,
(1)已知a2+a3+a23+a24=48,求a13;
(2)已知a2+a3+a4+a5=34,a2·a5=52,求d.
解:(1)根据已知条件a2+a3+a23+a24=48及a2+a24=a3+a23=2a13,
得4a13=48,
∴a13=12.
(2)已知a2+a3+a4+a5=34,a2·a5=52,求d.
(2)由a2+a3+a4+a5=34及a3+a4=a2+a5得2(a2+a5)=34,
即a2+a5=17.
例4 一个木制梯架的上、下两底边分别为33 cm,75cm,把梯形的两腰各6等分,用平行木条连接各对应分点,构成梯形架的各级.试计算梯形架间各级的宽度.
解:记梯形架自上而下各级宽度所构成的数列为{an},则由梯形中位线的性质,易知相邻三项均成等差数列,即数列{an}成等差数列.
依题意,有a1=33cm,a7=75cm,
现要求a2,a3,a4,a5,a6,即中间5级的宽度.由等差数列的定义,有
所以a2=33+7=40(cm),a3=40+7=47(cm),a4=47+7=54(cm),a5=54+7=61(cm),a6=61+7=68(cm).
因此梯形架中间各级的宽度自上而下依次是40cm,47cm,54cm,61cm,68cm.
例4 一个木制梯架的上、下两底边分别为33 cm,75cm,把梯形的两腰各6等分,用平行木条连接各对应分点,构成梯形架的各级.试计算梯形架间各级的宽度.
根据今天所学,回答下列问题:
1.什么是等差中项,怎样求等差中项?
2.等差数列的性质有哪些?
3.如何利用等差数列解决实际问题?
1.已知{an}为等差数列,a4+a7+a10=30,则a3-2a5的值为( )
A.10 B.-10 C.15 D.-15
2.等差数列20,17,14,11,…中第一个负数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
3.在等差数列{an}中,已知a4+a8=16,则a2+a10=________.
4.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )
A.1升 B.升 C.升 D.升
D
B
B
16
