【专项培优】人教版数学八年级下册第18章平行四边形(含答案)
文档属性
| 名称 | 【专项培优】人教版数学八年级下册第18章平行四边形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 413.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 09:00:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【专项培优】人教版数学八年级下册第18章平行四边形
一、单选题
1.(2023九上·迎泽期中)如图,将矩形ABCD沿对角线BD折叠,点A落在点E处,DE交BC于点F,若∠CFD=40°,则∠ABD的度数为( )
A.50° B.60° C.70° D.80°
2.(2024八下·大连月考)下列命题正确的是 ( )
A.两组对边分别相等的四边形是矩形
B.有一个角是直角的平行四边形是矩形
C.有两个角是直角的四边形是矩形
D.一组邻边相等的平行四边形是矩形
3.(2024九下·广西壮族自治区模拟)如图,在一次数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在外选择一点C,测得两边中点的距离为,则A,B两点的距离是( ).
A.12 B.14 C.16 D.24
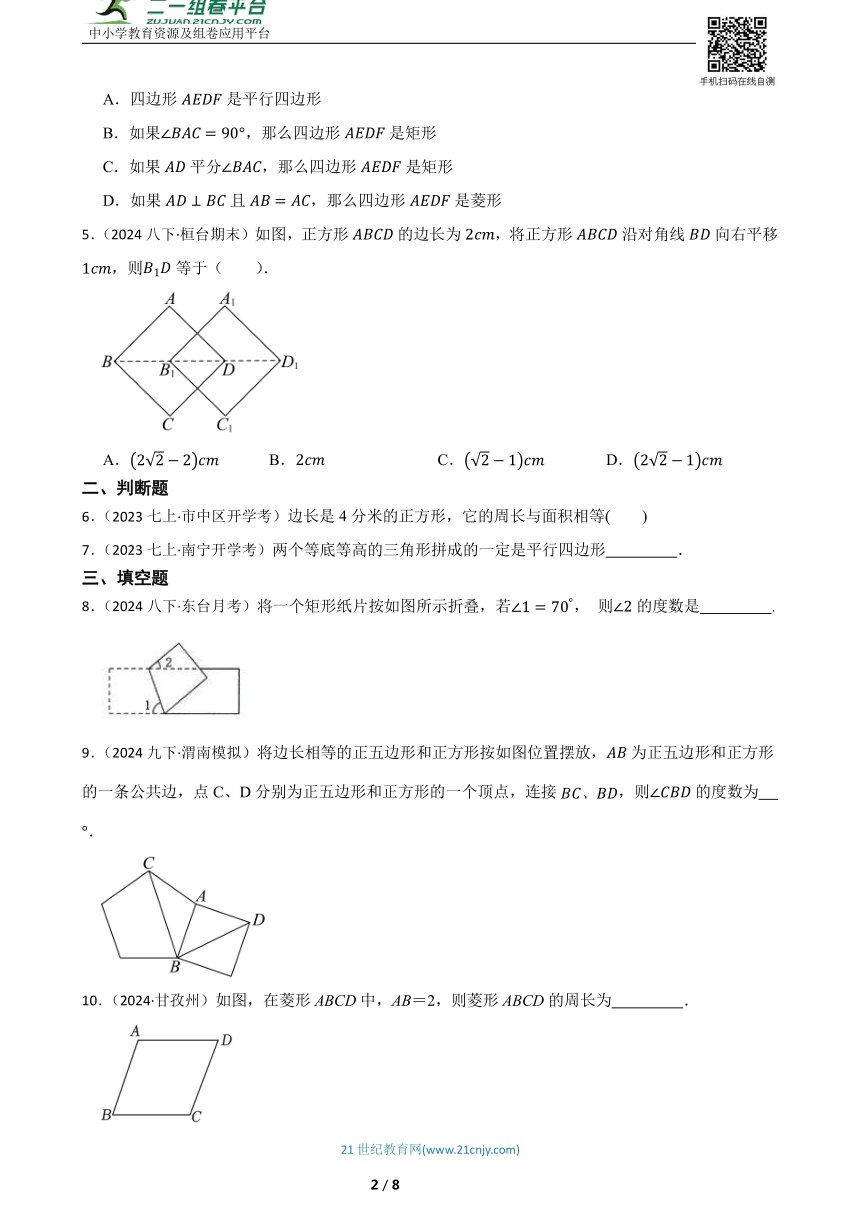
4.(2024八下·竹溪期中)如图,在中,点E,D,F分别在、、上,且,.下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分,那么四边形是矩形
D.如果且,那么四边形是菱形
5.(2024八下·桓台期末)如图,正方形的边长为,将正方形沿对角线向右平移,则等于( ).
A. B. C. D.
二、判断题
6.(2023七上·市中区开学考)边长是4分米的正方形,它的周长与面积相等( )
7.(2023七上·南宁开学考)两个等底等高的三角形拼成的一定是平行四边形 .
三、填空题
8.(2024八下·东台月考)将一个矩形纸片按如图所示折叠,若, 则的度数是 .
9.(2024九下·渭南模拟)将边长相等的正五边形和正方形按如图位置摆放,为正五边形和正方形的一条公共边,点C、D分别为正五边形和正方形的一个顶点,连接,则的度数为 .
10.(2024·甘孜州)如图,在菱形ABCD中,AB=2,则菱形ABCD的周长为 .
11.(2021八下·临汾期中)如图.在中,对角线、相交于点O,若,,,则的周长为 .
12.(2024八下·广州期中)在中,,则的度数为 .
13.(2024八下·惠来期末)如图,平行四边形中,平分交于点E,若,,则 .
四、计算题
14.(2024八下·长沙月考)如图,在平行四边形中,,,平分交于点,求的长.
15.(2024八上·南京月考)已知,如图所示,折叠长方形的一边,使点落在边的点处,已知,求:
(1)求的坐标;
(2)求的坐标.
五、解答题
16.(2022八下·钦南月考)如图,已知菱形的顶点,的坐标分别为,,点在轴上.
(1)求点的坐标;
(2)如图,对角线,相交于点,求,的长及点的坐标.
17.(2023八下·江海期中)如图,一块长方形场地的长与宽之比为,于点E,于点F,连结.现计划在四边形区域内种植花草,求四边形与长方形的面积之比.
六、综合题
18.(2023·武昌模拟)如图,在平行四边形中,的平分线交于点,交的延长线于点.
(1)求证:;
(2)若,求的度数.
19.(2023八下·临潼期末)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由
20.(2019·瑞安模拟)如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,AB=6,求四边形BEDF的周长.
七、实践探究题
21.小惠自编一题: “如图, 在四边形 中, 对角线 交于点 . 求证: 四边形 是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 小洁:
证明: , 这个题目还缺少条件, 需要补充一个条件才 能证明.
垂直平分 .
,
四边形 是菱形.
若赞同小惠的证法,请在第一个方框内打 “ √ ”;若赞成小洁的说法, 请你补充一个条件, 并证明.
答案解析部分
1.【答案】C
【知识点】矩形的性质
2.【答案】B
【知识点】平行四边形的判定;菱形的判定;矩形的判定
3.【答案】C
【知识点】三角形的中位线定理
4.【答案】C
【知识点】平行四边形的判定;菱形的判定;矩形的判定
5.【答案】D
【知识点】勾股定理;正方形的性质;平移的性质
6.【答案】错误
【知识点】正方形的性质
7.【答案】
【知识点】平行四边形的判定
8.【答案】40°
【知识点】矩形的性质
9.【答案】81
【知识点】多边形内角与外角;正方形的性质
10.【答案】8
【知识点】菱形的性质
11.【答案】21
【知识点】平行四边形的性质
12.【答案】
【知识点】平行四边形的性质
13.【答案】2
【知识点】平行四边形的性质
14.【答案】的长为3.
【知识点】等腰三角形的判定与性质;平行四边形的性质
15.【答案】(1)
(2)
【知识点】勾股定理;矩形的性质
16.【答案】(1)
(2),,.
【知识点】勾股定理;菱形的性质
17.【答案】
【知识点】二次根式的乘除法;平行四边形的判定与性质;矩形的性质
18.【答案】(1)证明:四边形是平行四边形,
,
,
平分,
,
,
;
(2)解:平分,
,∠ABC=2∠2,
∵四边形ABCD是平行四边形,
,
,
,,
,
,
.
四边形ABCD是平行四边形,
,
,
.
【知识点】等腰三角形的判定与性质;平行四边形的性质
19.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形
(2)解:当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形
【知识点】正方形的判定
20.【答案】(1)证明:在 ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
∴△ADE≌△CBF
(2)解:∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BE= AB,BF=DF= CD,
∴DE=BE=BF=DF=3,
∴四边形DEBF是菱形,周长为12.
【知识点】全等三角形的判定与性质;平行四边形的性质;直角三角形斜边上的中线
21.【答案】解:赞成小洁的说法, 补充条件: ,
证明如下:
,
四边形ABCD是平行四边形.
又
∴ 平行四边形 是菱形.
【知识点】菱形的判定
21世纪教育网(www.21cnjy.com)
1 / 8
【专项培优】人教版数学八年级下册第18章平行四边形
一、单选题
1.(2023九上·迎泽期中)如图,将矩形ABCD沿对角线BD折叠,点A落在点E处,DE交BC于点F,若∠CFD=40°,则∠ABD的度数为( )
A.50° B.60° C.70° D.80°
2.(2024八下·大连月考)下列命题正确的是 ( )
A.两组对边分别相等的四边形是矩形
B.有一个角是直角的平行四边形是矩形
C.有两个角是直角的四边形是矩形
D.一组邻边相等的平行四边形是矩形
3.(2024九下·广西壮族自治区模拟)如图,在一次数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在外选择一点C,测得两边中点的距离为,则A,B两点的距离是( ).
A.12 B.14 C.16 D.24
4.(2024八下·竹溪期中)如图,在中,点E,D,F分别在、、上,且,.下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分,那么四边形是矩形
D.如果且,那么四边形是菱形
5.(2024八下·桓台期末)如图,正方形的边长为,将正方形沿对角线向右平移,则等于( ).
A. B. C. D.
二、判断题
6.(2023七上·市中区开学考)边长是4分米的正方形,它的周长与面积相等( )
7.(2023七上·南宁开学考)两个等底等高的三角形拼成的一定是平行四边形 .
三、填空题
8.(2024八下·东台月考)将一个矩形纸片按如图所示折叠,若, 则的度数是 .
9.(2024九下·渭南模拟)将边长相等的正五边形和正方形按如图位置摆放,为正五边形和正方形的一条公共边,点C、D分别为正五边形和正方形的一个顶点,连接,则的度数为 .
10.(2024·甘孜州)如图,在菱形ABCD中,AB=2,则菱形ABCD的周长为 .
11.(2021八下·临汾期中)如图.在中,对角线、相交于点O,若,,,则的周长为 .
12.(2024八下·广州期中)在中,,则的度数为 .
13.(2024八下·惠来期末)如图,平行四边形中,平分交于点E,若,,则 .
四、计算题
14.(2024八下·长沙月考)如图,在平行四边形中,,,平分交于点,求的长.
15.(2024八上·南京月考)已知,如图所示,折叠长方形的一边,使点落在边的点处,已知,求:
(1)求的坐标;
(2)求的坐标.
五、解答题
16.(2022八下·钦南月考)如图,已知菱形的顶点,的坐标分别为,,点在轴上.
(1)求点的坐标;
(2)如图,对角线,相交于点,求,的长及点的坐标.
17.(2023八下·江海期中)如图,一块长方形场地的长与宽之比为,于点E,于点F,连结.现计划在四边形区域内种植花草,求四边形与长方形的面积之比.
六、综合题
18.(2023·武昌模拟)如图,在平行四边形中,的平分线交于点,交的延长线于点.
(1)求证:;
(2)若,求的度数.
19.(2023八下·临潼期末)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由
20.(2019·瑞安模拟)如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,AB=6,求四边形BEDF的周长.
七、实践探究题
21.小惠自编一题: “如图, 在四边形 中, 对角线 交于点 . 求证: 四边形 是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 小洁:
证明: , 这个题目还缺少条件, 需要补充一个条件才 能证明.
垂直平分 .
,
四边形 是菱形.
若赞同小惠的证法,请在第一个方框内打 “ √ ”;若赞成小洁的说法, 请你补充一个条件, 并证明.
答案解析部分
1.【答案】C
【知识点】矩形的性质
2.【答案】B
【知识点】平行四边形的判定;菱形的判定;矩形的判定
3.【答案】C
【知识点】三角形的中位线定理
4.【答案】C
【知识点】平行四边形的判定;菱形的判定;矩形的判定
5.【答案】D
【知识点】勾股定理;正方形的性质;平移的性质
6.【答案】错误
【知识点】正方形的性质
7.【答案】
【知识点】平行四边形的判定
8.【答案】40°
【知识点】矩形的性质
9.【答案】81
【知识点】多边形内角与外角;正方形的性质
10.【答案】8
【知识点】菱形的性质
11.【答案】21
【知识点】平行四边形的性质
12.【答案】
【知识点】平行四边形的性质
13.【答案】2
【知识点】平行四边形的性质
14.【答案】的长为3.
【知识点】等腰三角形的判定与性质;平行四边形的性质
15.【答案】(1)
(2)
【知识点】勾股定理;矩形的性质
16.【答案】(1)
(2),,.
【知识点】勾股定理;菱形的性质
17.【答案】
【知识点】二次根式的乘除法;平行四边形的判定与性质;矩形的性质
18.【答案】(1)证明:四边形是平行四边形,
,
,
平分,
,
,
;
(2)解:平分,
,∠ABC=2∠2,
∵四边形ABCD是平行四边形,
,
,
,,
,
,
.
四边形ABCD是平行四边形,
,
,
.
【知识点】等腰三角形的判定与性质;平行四边形的性质
19.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形
(2)解:当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形
【知识点】正方形的判定
20.【答案】(1)证明:在 ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
∴△ADE≌△CBF
(2)解:∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BE= AB,BF=DF= CD,
∴DE=BE=BF=DF=3,
∴四边形DEBF是菱形,周长为12.
【知识点】全等三角形的判定与性质;平行四边形的性质;直角三角形斜边上的中线
21.【答案】解:赞成小洁的说法, 补充条件: ,
证明如下:
,
四边形ABCD是平行四边形.
又
∴ 平行四边形 是菱形.
【知识点】菱形的判定
21世纪教育网(www.21cnjy.com)
1 / 8
