【专项培优】人教版数学八年级下册第20章数据的分析(含答案)
文档属性
| 名称 | 【专项培优】人教版数学八年级下册第20章数据的分析(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 08:59:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【专项培优】人教版数学八年级下册第20章数据的分析
一、单选题
1.(2024八下·赵县期末)已知两组数据(1),,,,;(2),,,,.设第一组数据的平均值为,方差为,设第二组数据的平均值为,方差为,下列结论正确的是( )
A., B.,
C., D.,
2.(2022八下·义乌期末)为了加强安全教育,某校组织以防溺水为主题的演讲比赛,参加决赛的7名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,8.3,9.5.这7名选手成绩的众数是( )
A.8.8分 B.9.5分 C.8.9分 D.9.0分
3.(2024九上·信都月考)下表是某公司25位员工收入的资料.
月收入/元 45000 18000 10000 5500 5000 3400 3000 1000
人数 1 1 1 3 6 1 11 1
能够反映该公司全体员工月收入水平的统计量是( )
A.平均数和众数 B.平均数和中位数
C.中位数和众数 D.平均数和方差
4.我市五月份连续五天的最高气温分别为23、20、20、21、26(单位: ),这组数据的中位数和众数分别是( )
A.22,26 B.22,20 C.21,26 D.21,20
5.(2022八下·钦州期末)某班10名学生的体育测试成绩分别为(单位:分)57,58.56,54,58,60,58,57,56,57,则这组数据的众数是( )
A.57 B.58 C.60 D.57,58
二、填空题
6.(2024八下·萧山月考)疫情期间居家学习,小兰和小丽积极进行体育锻炼,增强体质.她们进行1分钟跳绳比赛,每人5次跳绳成绩的平均数都是165个,方差分别是,,则这5次跳绳成绩更稳定的是 .(填“小兰”或“小丽”)
7.(2024八下·南乐期末)学校要选拔一名短跑运动员,参加校际联赛.小明、小亮、小龙、小江四位同学报名参加,老师对四位同学进行了百米测试,经过3场测试,计算出来他们的平均成绩及方差如下表:
小明 小亮 小龙 小江
根据表中数据,要选拔成绩好且发挥稳定的同学参加校际比赛,应选择 .
8.(2024八下·固始期末)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是环,方差分别为,,,,则成绩最稳定的是 .
9.(2017·乌拉特前旗模拟)一次数学模考后,刘老师统计了20名学生的成绩,记录如下:有6人得了85分,有5人得了80分,有4人得了65分,有5人得了90分.则这组数据的中位数和平均数分别是 .
10.(2021八下·青山期末)小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是S小刘2=0.6,S小李2=1.4,那么两人中射击成绩比较稳定的是 ;
11.(2022九上·黄冈开学考)如表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择 .
甲 乙 丙 丁
平均数(环) 9.14 9.15 9.14 9.15
方差 6.6 6.8 6.7 6.6
三、计算题
12.(2024八下·海曙月考)小青在本学期的数学成绩如下表所示(成绩均取整数):
测验类别 平时 期中考试 期末考试
测验1 测验1 测验1 课题学习
成绩 88 70 96 86 85
(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
13.(2022八下·金东期末)甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 93 89 90
学生乙 94 92 94 86
(1)分别求学生甲、乙成绩的中位数.
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按计算,那么甲、乙的数学综合素质成绩谁更好?
四、解答题
14.(2024九下·蚌山模拟)在一节体育课上,某班的名女同学的跳远成绩如表所示:
成绩
人数
求出这些女同学跳远成绩的众数、中位数和平均数.
15.(2022九上·海淀开学考)初二年级在小学段期间开展名著阅读比赛,从参赛的400名学生中抽取了部分学生的成绩进行分析,绘制了频数分布表与频数分布直方图.
成绩x(分) 频数
60≤x<70 3
70≤x<80 9
80≤x<90 a
90≤x<100 6
其中,成绩在80≤x<90这一组的是:
83 80 86 81 82 89
85 86 81 87 88 84
请根据图表信息解答下列问题:
(1)表中的a的值为 ;
(2)补全频数分布直方图;
(3)抽取的这部分学生成绩的中位数是 ;
(4)若成绩不低于85分属于优秀,估计初二年级参赛学生中有多少人达到优秀水平?
五、综合题
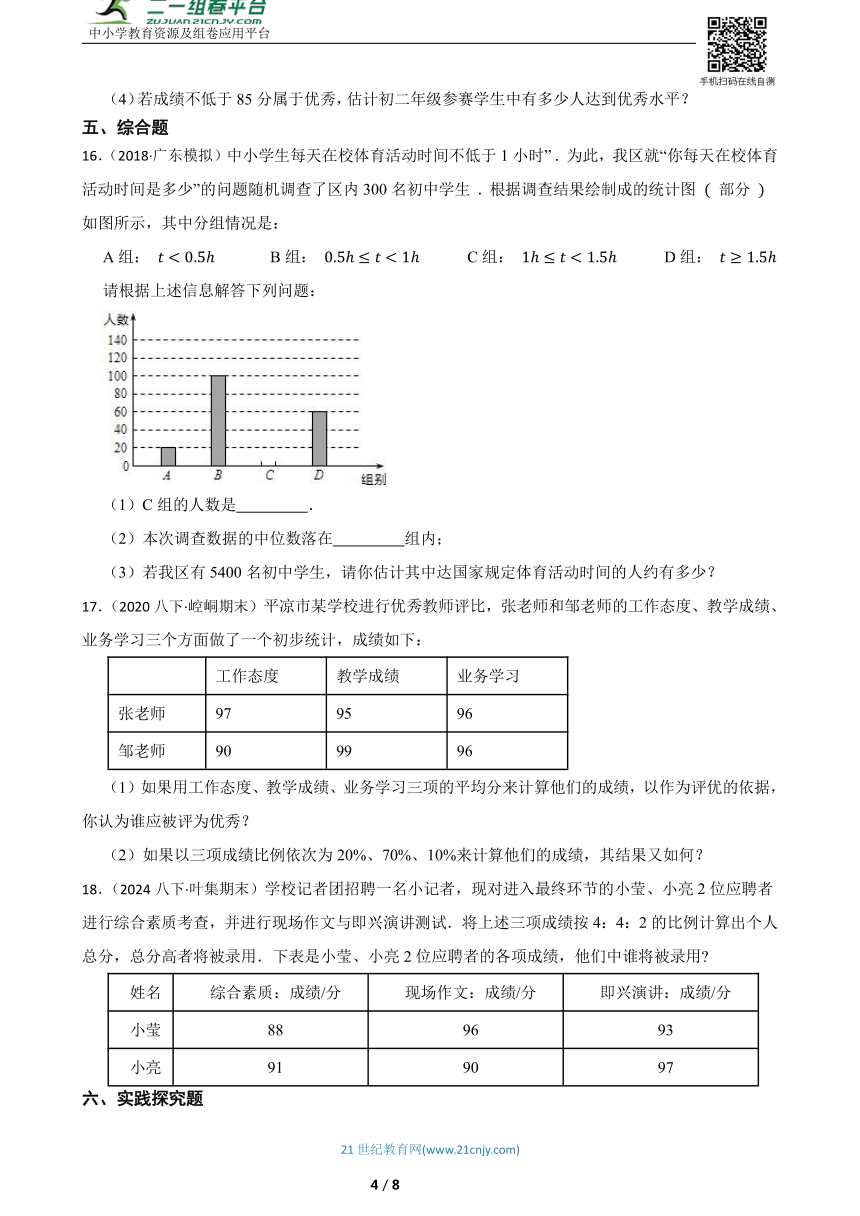
16.(2018·广东模拟)中小学生每天在校体育活动时间不低于1小时” 为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生 根据调查结果绘制成的统计图 部分 如图所示,其中分组情况是:
A组: B组: C组: D组:
请根据上述信息解答下列问题:
(1)C组的人数是 .
(2)本次调查数据的中位数落在 组内;
(3)若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
17.(2020八下·崆峒期末)平凉市某学校进行优秀教师评比,张老师和邹老师的工作态度、教学成绩、业务学习三个方面做了一个初步统计,成绩如下:
工作态度 教学成绩 业务学习
张老师 97 95 96
邹老师 90 99 96
(1)如果用工作态度、教学成绩、业务学习三项的平均分来计算他们的成绩,以作为评优的依据,你认为谁应被评为优秀?
(2)如果以三项成绩比例依次为20%、70%、10%来计算他们的成绩,其结果又如何?
18.(2024八下·叶集期末)学校记者团招聘一名小记者,现对进入最终环节的小莹、小亮2位应聘者进行综合素质考查,并进行现场作文与即兴演讲测试.将上述三项成绩按4:4:2的比例计算出个人总分,总分高者将被录用.下表是小莹、小亮2位应聘者的各项成绩,他们中谁将被录用
姓名 综合素质:成绩/分 现场作文:成绩/分 即兴演讲:成绩/分
小莹 88 96 93
小亮 91 90 97
六、实践探究题
19.(2023九下·玉州模拟)综合与实践
【问题情境】某校组织九年级800名学生开展体育中考前的“引体向上提升”训练活动.
【实践发现】为了考查训练效果,在进行提升训练前学校先组织全体学生进行了摸底测试,经过提升训练后再进行模拟考试,并用抽样调查的方式从中随机抽取了50名学生提升训练前后的摸底测试和模拟考试的成绩,收集整理后,制成如下表格:
摸底测试 成绩(个) 6 7 8 9 10
人数(人) 16 8 9 9 8
模拟考试 成绩(个) 6 7 8 9 10
人数(人) 5 8 6 12 19
【实践探究】分析数据如下:(单位:个数)
中位数 众数
摸底测试 a 6
模拟考试 9 b
(1)上述表格中,_____,_______;
(2)这50名学生经过训练后,模拟考试的平均成绩比摸底测试的平均成绩多多少个?
(3)若考试成绩达到9个以上(含9个)为优秀,请估计该校九年级800名学生经过训练后,模拟考试成绩优秀的人数约有多少人?
答案解析部分
1.【答案】D
【知识点】平均数及其计算;方差
2.【答案】A
【知识点】众数
3.【答案】C
【知识点】中位数;众数
4.【答案】D
【知识点】中位数;众数
5.【答案】D
【知识点】众数
6.【答案】小丽
【知识点】方差
7.【答案】小江或小明
【知识点】方差
8.【答案】丁
【知识点】方差
9.【答案】85;81
【知识点】平均数及其计算;中位数
10.【答案】小刘
【知识点】方差
11.【答案】丁
【知识点】方差
12.【答案】(1)85分(2)94分
【知识点】一元一次不等式的应用;加权平均数及其计算
13.【答案】(1)甲90;乙93
(2)乙的数学综合素质成绩更好
【知识点】加权平均数及其计算;中位数
14.【答案】众数为,中位数为,平均数为.
【知识点】平均数及其计算;中位数;众数
15.【答案】(1)12
(2)解:由(1)知,a=12,
补全的频数分布直方图如右图所示;
(3)81.5
(4)解:400×=160(名),
答:初二年级参赛学生中有160人达到优秀水平.
【知识点】用样本估计总体;频数(率)分布表;频数(率)分布直方图;中位数
16.【答案】(1)120
(2)C
(3)解:达国家规定体育活动时间的人数约占 .
所以,达国家规定体育活动时间的人约有 人 .
【知识点】用样本估计总体;频数(率)分布直方图;中位数
17.【答案】(1)解: 分, 分,
显然张老师的得分比邹老师的得分高,因而张老师应被评为优秀
(2)解: 分,
分,
由于邹老师的得分比张老师的得分高,因而邹老师应被评为优秀
【知识点】平均数及其计算;加权平均数及其计算
18.【答案】小莹将被录用.
【知识点】加权平均数及其计算
19.【答案】(1)
(2)个
(3)496人
【知识点】频数(率)分布表;加权平均数及其计算;中位数;众数
21世纪教育网(www.21cnjy.com)
1 / 8
【专项培优】人教版数学八年级下册第20章数据的分析
一、单选题
1.(2024八下·赵县期末)已知两组数据(1),,,,;(2),,,,.设第一组数据的平均值为,方差为,设第二组数据的平均值为,方差为,下列结论正确的是( )
A., B.,
C., D.,
2.(2022八下·义乌期末)为了加强安全教育,某校组织以防溺水为主题的演讲比赛,参加决赛的7名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,8.3,9.5.这7名选手成绩的众数是( )
A.8.8分 B.9.5分 C.8.9分 D.9.0分
3.(2024九上·信都月考)下表是某公司25位员工收入的资料.
月收入/元 45000 18000 10000 5500 5000 3400 3000 1000
人数 1 1 1 3 6 1 11 1
能够反映该公司全体员工月收入水平的统计量是( )
A.平均数和众数 B.平均数和中位数
C.中位数和众数 D.平均数和方差
4.我市五月份连续五天的最高气温分别为23、20、20、21、26(单位: ),这组数据的中位数和众数分别是( )
A.22,26 B.22,20 C.21,26 D.21,20
5.(2022八下·钦州期末)某班10名学生的体育测试成绩分别为(单位:分)57,58.56,54,58,60,58,57,56,57,则这组数据的众数是( )
A.57 B.58 C.60 D.57,58
二、填空题
6.(2024八下·萧山月考)疫情期间居家学习,小兰和小丽积极进行体育锻炼,增强体质.她们进行1分钟跳绳比赛,每人5次跳绳成绩的平均数都是165个,方差分别是,,则这5次跳绳成绩更稳定的是 .(填“小兰”或“小丽”)
7.(2024八下·南乐期末)学校要选拔一名短跑运动员,参加校际联赛.小明、小亮、小龙、小江四位同学报名参加,老师对四位同学进行了百米测试,经过3场测试,计算出来他们的平均成绩及方差如下表:
小明 小亮 小龙 小江
根据表中数据,要选拔成绩好且发挥稳定的同学参加校际比赛,应选择 .
8.(2024八下·固始期末)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是环,方差分别为,,,,则成绩最稳定的是 .
9.(2017·乌拉特前旗模拟)一次数学模考后,刘老师统计了20名学生的成绩,记录如下:有6人得了85分,有5人得了80分,有4人得了65分,有5人得了90分.则这组数据的中位数和平均数分别是 .
10.(2021八下·青山期末)小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是S小刘2=0.6,S小李2=1.4,那么两人中射击成绩比较稳定的是 ;
11.(2022九上·黄冈开学考)如表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择 .
甲 乙 丙 丁
平均数(环) 9.14 9.15 9.14 9.15
方差 6.6 6.8 6.7 6.6
三、计算题
12.(2024八下·海曙月考)小青在本学期的数学成绩如下表所示(成绩均取整数):
测验类别 平时 期中考试 期末考试
测验1 测验1 测验1 课题学习
成绩 88 70 96 86 85
(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
13.(2022八下·金东期末)甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 93 89 90
学生乙 94 92 94 86
(1)分别求学生甲、乙成绩的中位数.
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按计算,那么甲、乙的数学综合素质成绩谁更好?
四、解答题
14.(2024九下·蚌山模拟)在一节体育课上,某班的名女同学的跳远成绩如表所示:
成绩
人数
求出这些女同学跳远成绩的众数、中位数和平均数.
15.(2022九上·海淀开学考)初二年级在小学段期间开展名著阅读比赛,从参赛的400名学生中抽取了部分学生的成绩进行分析,绘制了频数分布表与频数分布直方图.
成绩x(分) 频数
60≤x<70 3
70≤x<80 9
80≤x<90 a
90≤x<100 6
其中,成绩在80≤x<90这一组的是:
83 80 86 81 82 89
85 86 81 87 88 84
请根据图表信息解答下列问题:
(1)表中的a的值为 ;
(2)补全频数分布直方图;
(3)抽取的这部分学生成绩的中位数是 ;
(4)若成绩不低于85分属于优秀,估计初二年级参赛学生中有多少人达到优秀水平?
五、综合题
16.(2018·广东模拟)中小学生每天在校体育活动时间不低于1小时” 为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生 根据调查结果绘制成的统计图 部分 如图所示,其中分组情况是:
A组: B组: C组: D组:
请根据上述信息解答下列问题:
(1)C组的人数是 .
(2)本次调查数据的中位数落在 组内;
(3)若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
17.(2020八下·崆峒期末)平凉市某学校进行优秀教师评比,张老师和邹老师的工作态度、教学成绩、业务学习三个方面做了一个初步统计,成绩如下:
工作态度 教学成绩 业务学习
张老师 97 95 96
邹老师 90 99 96
(1)如果用工作态度、教学成绩、业务学习三项的平均分来计算他们的成绩,以作为评优的依据,你认为谁应被评为优秀?
(2)如果以三项成绩比例依次为20%、70%、10%来计算他们的成绩,其结果又如何?
18.(2024八下·叶集期末)学校记者团招聘一名小记者,现对进入最终环节的小莹、小亮2位应聘者进行综合素质考查,并进行现场作文与即兴演讲测试.将上述三项成绩按4:4:2的比例计算出个人总分,总分高者将被录用.下表是小莹、小亮2位应聘者的各项成绩,他们中谁将被录用
姓名 综合素质:成绩/分 现场作文:成绩/分 即兴演讲:成绩/分
小莹 88 96 93
小亮 91 90 97
六、实践探究题
19.(2023九下·玉州模拟)综合与实践
【问题情境】某校组织九年级800名学生开展体育中考前的“引体向上提升”训练活动.
【实践发现】为了考查训练效果,在进行提升训练前学校先组织全体学生进行了摸底测试,经过提升训练后再进行模拟考试,并用抽样调查的方式从中随机抽取了50名学生提升训练前后的摸底测试和模拟考试的成绩,收集整理后,制成如下表格:
摸底测试 成绩(个) 6 7 8 9 10
人数(人) 16 8 9 9 8
模拟考试 成绩(个) 6 7 8 9 10
人数(人) 5 8 6 12 19
【实践探究】分析数据如下:(单位:个数)
中位数 众数
摸底测试 a 6
模拟考试 9 b
(1)上述表格中,_____,_______;
(2)这50名学生经过训练后,模拟考试的平均成绩比摸底测试的平均成绩多多少个?
(3)若考试成绩达到9个以上(含9个)为优秀,请估计该校九年级800名学生经过训练后,模拟考试成绩优秀的人数约有多少人?
答案解析部分
1.【答案】D
【知识点】平均数及其计算;方差
2.【答案】A
【知识点】众数
3.【答案】C
【知识点】中位数;众数
4.【答案】D
【知识点】中位数;众数
5.【答案】D
【知识点】众数
6.【答案】小丽
【知识点】方差
7.【答案】小江或小明
【知识点】方差
8.【答案】丁
【知识点】方差
9.【答案】85;81
【知识点】平均数及其计算;中位数
10.【答案】小刘
【知识点】方差
11.【答案】丁
【知识点】方差
12.【答案】(1)85分(2)94分
【知识点】一元一次不等式的应用;加权平均数及其计算
13.【答案】(1)甲90;乙93
(2)乙的数学综合素质成绩更好
【知识点】加权平均数及其计算;中位数
14.【答案】众数为,中位数为,平均数为.
【知识点】平均数及其计算;中位数;众数
15.【答案】(1)12
(2)解:由(1)知,a=12,
补全的频数分布直方图如右图所示;
(3)81.5
(4)解:400×=160(名),
答:初二年级参赛学生中有160人达到优秀水平.
【知识点】用样本估计总体;频数(率)分布表;频数(率)分布直方图;中位数
16.【答案】(1)120
(2)C
(3)解:达国家规定体育活动时间的人数约占 .
所以,达国家规定体育活动时间的人约有 人 .
【知识点】用样本估计总体;频数(率)分布直方图;中位数
17.【答案】(1)解: 分, 分,
显然张老师的得分比邹老师的得分高,因而张老师应被评为优秀
(2)解: 分,
分,
由于邹老师的得分比张老师的得分高,因而邹老师应被评为优秀
【知识点】平均数及其计算;加权平均数及其计算
18.【答案】小莹将被录用.
【知识点】加权平均数及其计算
19.【答案】(1)
(2)个
(3)496人
【知识点】频数(率)分布表;加权平均数及其计算;中位数;众数
21世纪教育网(www.21cnjy.com)
1 / 8
