4.1.1 平行线 课件(共22张PPT)
文档属性
| 名称 | 4.1.1 平行线 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 17:42:16 | ||
图片预览






文档简介
(共22张PPT)
平行线
七年级下册 第四章 4.1.1
学习目标
1.理解平行线的概念。
2.掌握平行线基本事实:过直线外一点有且只有一条直线与这条直线平行。
3.能用尺规作图:过直线外一点作这条直线的平行线。
4.了解平行于同一条直线的两条直线平行。
问题导入
直线a和直线b只有一个公共点,它们的位置关系是什么?
回顾
相交
如果两条直线只有一个公共点,那么称这两条直线相交,也称它们是相交直线,这个公共点叫作它们的交点.
新知探究
思考:如果两条直线有两个公共点,那么这两条直线的位置关系是什么?
如果两条直线有两个公共点,那么由“两点确定一条直线”可知,它们一定重合.
如果没有特别说明,两条重合的直线只当作一条.
新知探究
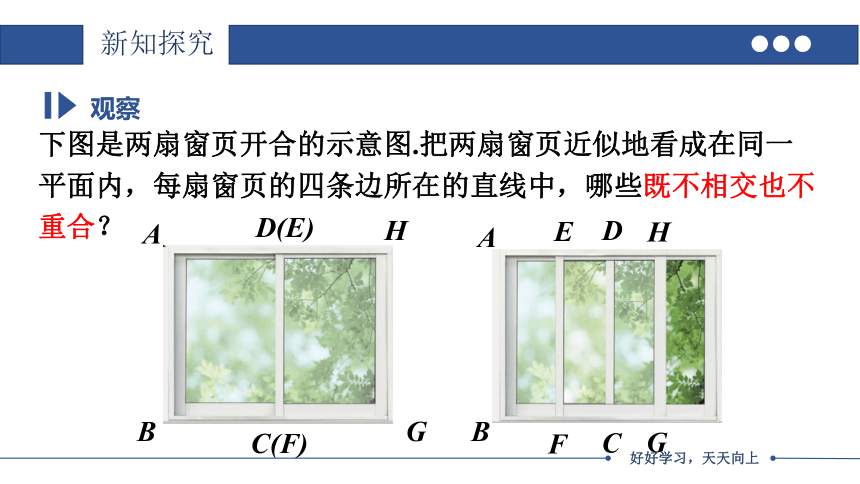
下图是两扇窗页开合的示意图.把两扇窗页近似地看成在同一平面内,每扇窗页的四条边所在的直线中,哪些既不相交也不重合?
观察
A
B
C(F)
D(E)
H
G
A
B
F
C
G
E
D
H
新知探究
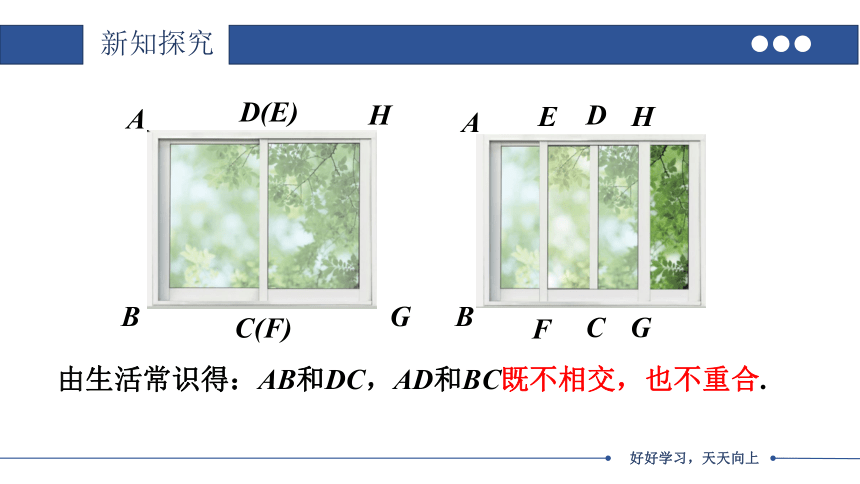
由生活常识得:AB和DC,AD和BC既不相交,也不重合.
A
B
C(F)
D(E)
H
G
A
B
F
C
G
E
D
H
新知探究
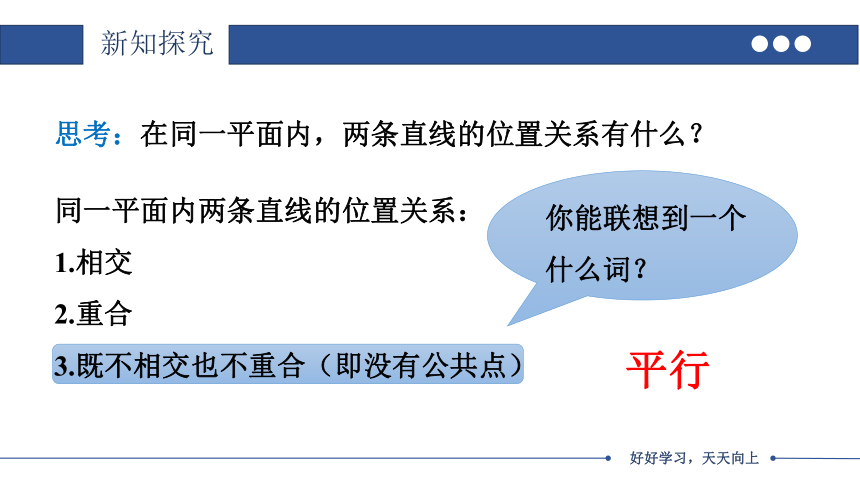
思考:在同一平面内,两条直线的位置关系有什么?
同一平面内两条直线的位置关系:
1.相交
2.重合
3.既不相交也不重合(即没有公共点)
你能联想到一个什么词?
平行
新知探究
在同一平面内,没有公共点的两条直线叫作平行线.平行用符号“∥ ”表示.
如图,直线AB与CD平行,记作“AB∥ CD”,读作“AB平行于CD”或“CD平行于AB”或“AB与CD互相平行”.
新知探究
日常生活中平行线的实例随处可见.例如,一段笔直铁路上的两条铁轨所在的直线,以及一排间隔相同、粗细均匀的栅栏竖条所在的直线.
铁轨
栅栏
新知探究
议一议
观察教室黑板的上、下边缘所在的直线,它们可以看作平行线吗?你还能从教室里找到哪些平行线的实例?将结果与同学交流.
如课桌上下边缘所在的直线、书本左右边缘所在的直线……
新知探究
思考
如图,任意画一条直线a,并在直线a外任取一点P.请用三角板和直尺画一条过点P且与直线a平行的直线.
新知探究
一般步骤
(1)把三角板的BC边靠紧直线a,再用直尺(或另一块三角板)靠紧三角板的另一边AC;
(2)沿直尺推动三角板,使原来和直线a重合的一边经过点P;
(3)沿三角板的这条边画直线b,则直线b就是过点P且与直线a平行的直线.
新知探究
你还可以画出其他过点P且与直线a平行的直线吗?
基本事实:
过直线外一点有且只有一条直线与这条直线平行.
新知探究
说一说
如图,如果直线a和c都与直线b平行,那么a与c平行吗?为什么?
c
·P
a
b
若a与c不平行,就会相交于某一点P(如图),那么过点P就有两条直线与b平行,根据平行线的基本事实,这是不可能的.因此a∥c.
新知探究
传递性
平行于同一条直线的两条直线平行.
如果a∥b,c∥b,那么a∥c.
c
a
b
课堂小结
这节课你收获了什么?
同一平面内两条直线的位置关系:
1.相交
2.重合
3.平行
课堂小结
基本事实:
过直线外一点有且只有一条直线与这条直线平行.
推论:
平行于同一条直线的两条直线平行.
如果a∥b,c∥b,那么a∥c.
课堂练习
1.下列说法中正确的是 ( )
A. 在同一平面内,两条不平行的线段必相交
B. 在同一平面内,不相交的两条线段必平行
C. 在同一平面内,不平行的两条射线必相交
D. 两条射线或线段平行,是指它们所在的直线平行
D
课堂练习
2.下列关于平行线的表示方法正确的是 ( )
A.a∥ A
B.AB∥ cd
C.A∥ B
D.a∥ b
D
一条直线可以用两个大写字母或者一个小写字母表示
课堂练习
3.若下列说法均不考虑重合的情况,则其中正确的说法个数为 ( )
①不相交的两条线是平行线;
②若线段AB与CD没有交点,则AB CD;
③若a b,b c,则a与c不相交.
A. 0 B. 1 C. 2 D. 3
B
课后作业
课堂作业:P92 T2、3
家庭作业:《学法》P54——55 A组(基础一般)
B组(基础较好)
C组(选做)
平行线
七年级下册 第四章 4.1.1
学习目标
1.理解平行线的概念。
2.掌握平行线基本事实:过直线外一点有且只有一条直线与这条直线平行。
3.能用尺规作图:过直线外一点作这条直线的平行线。
4.了解平行于同一条直线的两条直线平行。
问题导入
直线a和直线b只有一个公共点,它们的位置关系是什么?
回顾
相交
如果两条直线只有一个公共点,那么称这两条直线相交,也称它们是相交直线,这个公共点叫作它们的交点.
新知探究
思考:如果两条直线有两个公共点,那么这两条直线的位置关系是什么?
如果两条直线有两个公共点,那么由“两点确定一条直线”可知,它们一定重合.
如果没有特别说明,两条重合的直线只当作一条.
新知探究
下图是两扇窗页开合的示意图.把两扇窗页近似地看成在同一平面内,每扇窗页的四条边所在的直线中,哪些既不相交也不重合?
观察
A
B
C(F)
D(E)
H
G
A
B
F
C
G
E
D
H
新知探究
由生活常识得:AB和DC,AD和BC既不相交,也不重合.
A
B
C(F)
D(E)
H
G
A
B
F
C
G
E
D
H
新知探究
思考:在同一平面内,两条直线的位置关系有什么?
同一平面内两条直线的位置关系:
1.相交
2.重合
3.既不相交也不重合(即没有公共点)
你能联想到一个什么词?
平行
新知探究
在同一平面内,没有公共点的两条直线叫作平行线.平行用符号“∥ ”表示.
如图,直线AB与CD平行,记作“AB∥ CD”,读作“AB平行于CD”或“CD平行于AB”或“AB与CD互相平行”.
新知探究
日常生活中平行线的实例随处可见.例如,一段笔直铁路上的两条铁轨所在的直线,以及一排间隔相同、粗细均匀的栅栏竖条所在的直线.
铁轨
栅栏
新知探究
议一议
观察教室黑板的上、下边缘所在的直线,它们可以看作平行线吗?你还能从教室里找到哪些平行线的实例?将结果与同学交流.
如课桌上下边缘所在的直线、书本左右边缘所在的直线……
新知探究
思考
如图,任意画一条直线a,并在直线a外任取一点P.请用三角板和直尺画一条过点P且与直线a平行的直线.
新知探究
一般步骤
(1)把三角板的BC边靠紧直线a,再用直尺(或另一块三角板)靠紧三角板的另一边AC;
(2)沿直尺推动三角板,使原来和直线a重合的一边经过点P;
(3)沿三角板的这条边画直线b,则直线b就是过点P且与直线a平行的直线.
新知探究
你还可以画出其他过点P且与直线a平行的直线吗?
基本事实:
过直线外一点有且只有一条直线与这条直线平行.
新知探究
说一说
如图,如果直线a和c都与直线b平行,那么a与c平行吗?为什么?
c
·P
a
b
若a与c不平行,就会相交于某一点P(如图),那么过点P就有两条直线与b平行,根据平行线的基本事实,这是不可能的.因此a∥c.
新知探究
传递性
平行于同一条直线的两条直线平行.
如果a∥b,c∥b,那么a∥c.
c
a
b
课堂小结
这节课你收获了什么?
同一平面内两条直线的位置关系:
1.相交
2.重合
3.平行
课堂小结
基本事实:
过直线外一点有且只有一条直线与这条直线平行.
推论:
平行于同一条直线的两条直线平行.
如果a∥b,c∥b,那么a∥c.
课堂练习
1.下列说法中正确的是 ( )
A. 在同一平面内,两条不平行的线段必相交
B. 在同一平面内,不相交的两条线段必平行
C. 在同一平面内,不平行的两条射线必相交
D. 两条射线或线段平行,是指它们所在的直线平行
D
课堂练习
2.下列关于平行线的表示方法正确的是 ( )
A.a∥ A
B.AB∥ cd
C.A∥ B
D.a∥ b
D
一条直线可以用两个大写字母或者一个小写字母表示
课堂练习
3.若下列说法均不考虑重合的情况,则其中正确的说法个数为 ( )
①不相交的两条线是平行线;
②若线段AB与CD没有交点,则AB CD;
③若a b,b c,则a与c不相交.
A. 0 B. 1 C. 2 D. 3
B
课后作业
课堂作业:P92 T2、3
家庭作业:《学法》P54——55 A组(基础一般)
B组(基础较好)
C组(选做)
同课章节目录
