第十七章勾股定理章节期中练习(含解析)
文档属性
| 名称 | 第十七章勾股定理章节期中练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 265.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十七章勾股定理章节期中练习人教版2024—2025学年八年级下册
一、选择题
1.以下列各组数为边长的三角形中,是直角三角形的是( )
A.0.3,0.4,0.5 B.5,6,11
C.2,, D.4,5,6
2.满足下列条件的△ABC,不是直角三角形的为( )
A.∠A=∠B﹣∠C B.∠A:∠B:∠C=1:1:2
C.b2=a2﹣c2 D.a:b:c=2:3:4
3.如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D.2.5
4.在△ABC中,AB=12,BC=16,AC=20,则△ABC的面积是( )
A.120 B.160 C.216 D.96
5.丽丽想知道学校旗杆的高,她发现旗杆顶端上的绳子垂直到地面还多2米,当她把绳子的下端拉开离旗杆6米后,发现下端刚好接触地面,则旗杆的高为( )
A.4米 B.8米 C.10米 D.12米
6.如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=16.则S3=( )
A.20 B.12 C.2 D.2
7.在Rt△ABC中,∠C=90°,AC=2,BC=4,则点C到斜边AB的距离是( )
A. B.2 C. D.
8.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长是( )
A.3cm B.4cm C.5cm D.6cm
二、填空题
9.如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形ABC中,AC=17,BC=15,则阴影部分的面积是 .
10.若三角形的两边长为4和5,要使其成为直角三角形,则第三边的长为 .
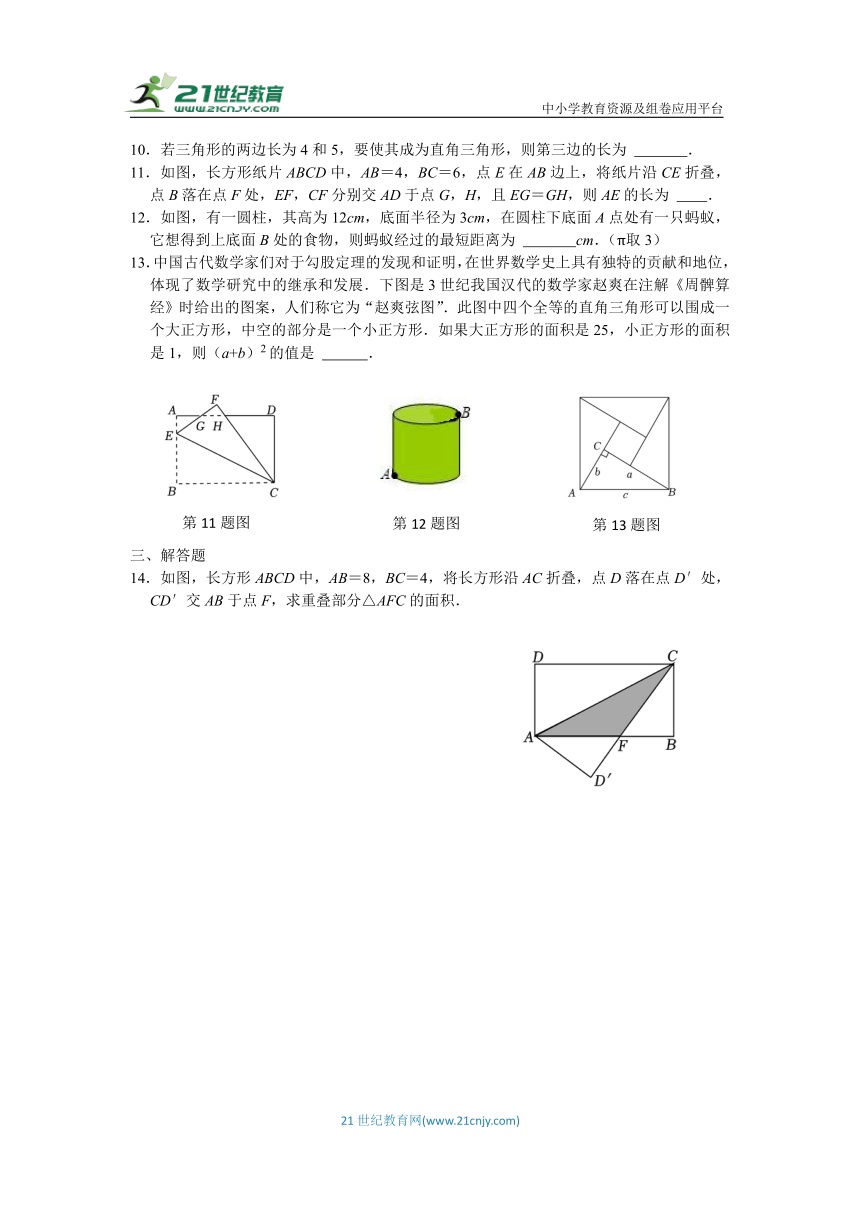
11.如图,长方形纸片ABCD中,AB=4,BC=6,点E在AB边上,将纸片沿CE折叠,点B落在点F处,EF,CF分别交AD于点G,H,且EG=GH,则AE的长为 .
12.如图,有一圆柱,其高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为 cm.(π取3)
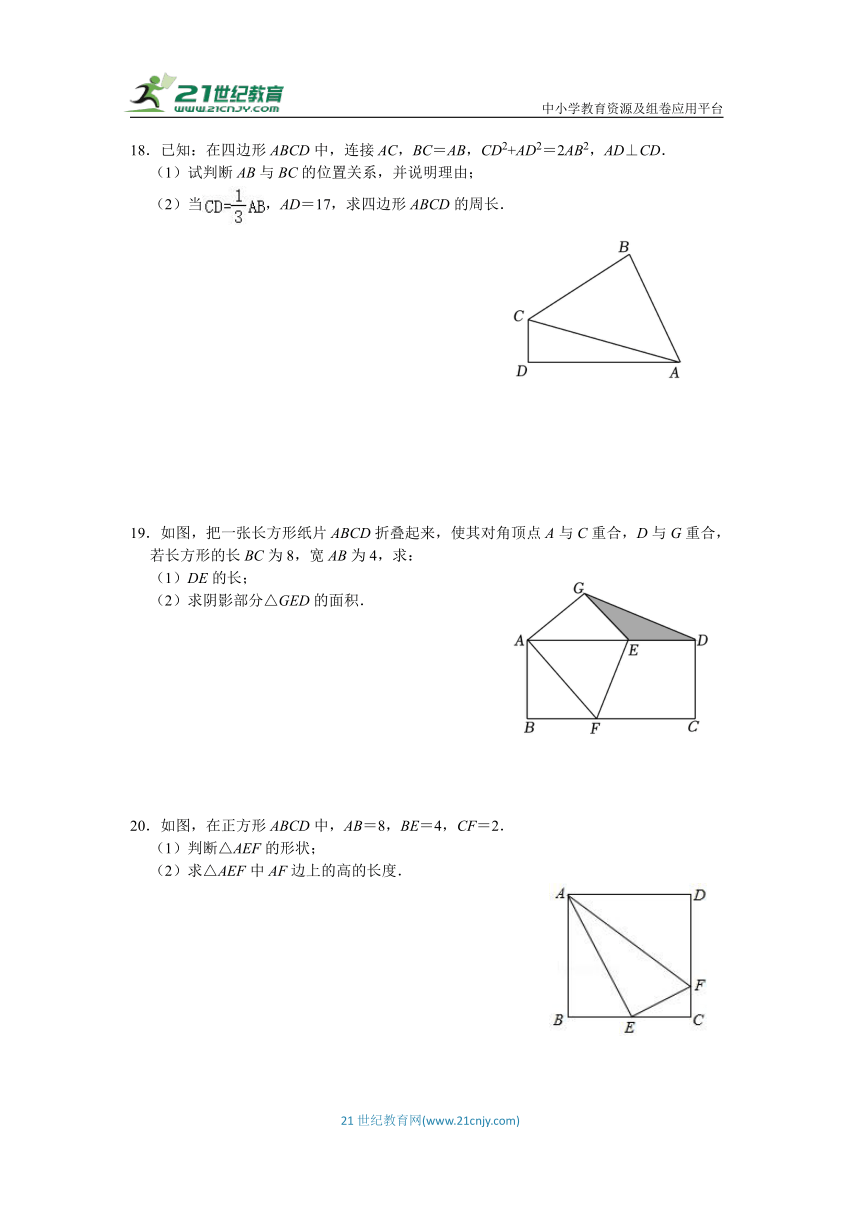
13.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.下图是3世纪我国汉代的数学家赵爽在注解《周髀算经》时给出的图案,人们称它为“赵爽弦图”.此图中四个全等的直角三角形可以围成一个大正方形,中空的部分是一个小正方形.如果大正方形的面积是25,小正方形的面积是1,则(a+b)2的值是 .
三、解答题
14.如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,CD′交AB于点F,求重叠部分△AFC的面积.
15.拖拉机行驶过程中会对周围产生较大的噪声影响.如图.有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域.
(1)求∠ACB度数;
(2)学校C会受噪声影响吗?为什么?
(3)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
16.如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
17.如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
18.已知:在四边形ABCD中,连接AC,BC=AB,CD2+AD2=2AB2,AD⊥CD.
(1)试判断AB与BC的位置关系,并说明理由;
(2)当,AD=17,求四边形ABCD的周长.
19.如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求:
(1)DE的长;
(2)求阴影部分△GED的面积.
20.如图,在正方形ABCD中,AB=8,BE=4,CF=2.
(1)判断△AEF的形状;
(2)求△AEF中AF边上的高的长度.
参考答案
一、选择题
1.【解答】解:A、∵0.32+0.42=0.52,
∴能构成直角三角形;符合题意;
B、∵52+62=61≠112,
∴不能构成直角三角形;不符合题意;
C、∵22+()2=9≠()2,
∴不能构成直角三角形;不符合题意;
D、∵42+52=41≠62,
∴不能构成直角三角形.不符合题意;
故选:A.
2.【解答】解:A、∠A=∠B﹣∠C,△ABC是直角三角形;
B、∠A:∠B:∠C=1:1:2,△ABC是直角三角形;
C、b2=a2﹣c2得b2+c2=a2,△ABC是直角三角形;
D:a:b:c=2:3:4,a=2x,那么b=3x,c=4x,a2+b2=13x2,c2=16x2,可证△ABC 不是直角三角形;
故选:D.
3.【解答】解:∵四边形OABC是矩形,
∴∠OAB=90°,
∴OB===,
∴这个点表示的示数是,
故选:C.
4.【解答】解:∵122+162=202,即AC2=AB2+BC2,
∴△ABC是直角三角形,且AC是直角边,
∴△ABC的面积是×12×16=96.
故选:D.
5.【解答】解:设旗杆的高为xm,则绳子的长为(x+2)m.
根据题意得:
x2+62=(x+2)2,
解得x=8.
故旗杆的高为8米.
故选:B.
6.【解答】解:∵∠ACB=90°,
∴BC2+AC2=AB2,
即4+16=20=AB2,
∴S3=20,
故选:A.
7.【解答】解:设点C到斜边AB的距离是h,
在Rt△ABC中,∠C=90°,AC=2,BC=4,
则由勾股定理,得AB==2,
由AC BC=AB h得到:h===.
故选:D.
8.【解答】解:∵四边形MNEF是由四边形ADMN折叠而成的,
∴DN=NE.
∵E是BC的中点且BC=8cm,
∴EC=4cm.
∵四边形ABCD是正方形,
∴∠BCD=90°.
设CN的长度为x cm,则EN=DN=(8﹣x)cm,
由勾股定理NC2+EC2=NE2,得x2+42=(8﹣x)2,
解得x=3.
故选:A.
二、填空题
9.【解答】解:由勾股定理得,AB2=AC2﹣BC2=172﹣152=64,
∵四边形ABFD为正方形,
∴DF=AB,
∴阴影部分的面积=DE2+EF2=DF2=64,
故答案为:64.
10.【解答】解:当4和5为直角边时,
第三边长为=;
当5为斜边,4为直角边时,
第三边长为=3.
故答案为:3或.
11.【解答】解:由题意可知,∠A=∠D=90°,AB=CD=4,AD=BC=6,
∵将△CBE沿CE翻折至△CFE,
∴∠F=∠B=∠A=90°,BE=EF,
又∵EG=GH,∠AGE=∠FGH,
∴△AGE≌△FGH(AAS),
∴FH=AE,GF=AG,
∴AH=BE=EF,
设AE=FH=x,则AH=BE=EF=4﹣x,
∴DH=AD﹣AH=x+2,CH=CF﹣FH=6﹣x,
∵CD2+DH2=CH2,
∴42+(2+x)2=(6﹣x)2,
解得:x=1,
∴AE=1,
故答案为:1.
12.【解答】解:圆柱展开图为长方形,
则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πrcm,
蚂蚁经过的最短距离为连接A,B的线段长,
由勾股定理得AB====15cm.
故蚂蚁经过的最短距离为15cm.
13.【解答】解:由图可得,
a2+b2=c2,c2=25,
∴a2+b2=25,
∵小正方形的面积是1,
∴(a﹣b)2=1,
∴a2﹣2ab+b2=1,
∴ab=12,
∴(a+b)2
=a2+2ab+b2
=(a2+b2)+2ab
=25+2×12
=25+24
=49,
故答案为:49.
三、解答题
14.【解答】解:由折叠和矩形的性质可知,∠D'=∠D=∠B=90°,AD'=CB=4,
又∵∠AFD'=∠CFB,
∴△AD'F≌△CBF(AAS),
∴AF=CF,
设BF=x,则AF=CF=8﹣x,
在Rt△CBF中,由勾股定理,得:x2+42=(8﹣x)2,
解得:x=3,
∴;
故重叠部分△AFC的面积为10.
15.【解答】解:(1)∵AC=150m,BC=200m,AB=250m,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°;
(2)学校C会受噪声影响.
理由:如图,过点C作CD⊥AB于D,
∴AC×BC=CD×AB,
∴150×200=250×CD,
∴CD==120(m),
∵拖拉机周围130m以内为受噪声影响区域,
∴学校C会受噪声影响.
(2)当EC=130m,FC=130m时,正好影响C学校,
∵ED=(m),
∴EF=100(m),
∵拖拉机的行驶速度为每分钟50米,
∴100÷50=2(分钟),
即拖拉机噪声影响该学校持续的时间有2分钟.
16.【解答】解:依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE===6,
∴CE=4,
∴E(4,8).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(8﹣OD)2+42=OD2,
∴OD=5,
∴D(0,5),
综上D点坐标为(0,5)、E点坐标为(4,8).
17.【解答】解:(1)由题意知,AB=(x+10)米,
在Rt△AOB中,由勾股定理得,
OB2+OA2=AB2,
即x2+202=(x+10)2,
解得x=15,
∴OB的长度为15米;
(2)由题意知,OC=AO﹣AC=20﹣5=15(米),CD=AB=25米,
在Rt△OCD中,由勾股定理得,
OC2+OD2=CD2,
即152+OD2=252,
解得OD=20米(负值舍去),
∴BD=20﹣15=5(米),
∴云梯的底部B往外移动了5米.
18.【解答】解:(1)AB⊥BC,理由如下:
∵AD⊥CD,
∴AD2+CD2=AC2,
∵CD2+AD2=2AB2,
∴AC2=2AB2,
∵BC=AB,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,且∠ABC=90°,
∴AB⊥BC;
(2)由(1)可知,∠ABC=90°,AD⊥CD,
∴CD2+AD2=AB2+BC2,
∵,AD=17,
∴CD2+172=(3CD)2+(3CD)2,
解得:,
∴,
∴四边形ABCD的周长=.
19.【解答】解:(1)设DE=EG=x,则AE=8﹣x,
在Rt△AEG中,AG2+EG2=AE2,
∴16+x2=(8﹣x)2,
解得x=3,
∴DE=3.
(2)过G点作GM⊥AD于M,
则 AG×GE= AE×GM,AG=AB=4,AE=CF=5,GE=DE=3,
∴GM=,
∴S△GED=GM×DE=.
20.【解答】解:(1)△AEF是直角三角形,理由如下:
∵四边形ABCD是正方形,AB=8,BE=4,CF=2.
∴EC=4,DF=6,
根据勾股定理可得:AE==4,
同理可得:EF=2,AF=10,
∴EF2+AE2=AF2,
∴△AEF是直角三角形;
(2)如图,过点E作EH⊥AF交AF于点H,
∵△AEF是直角三角形,
∴S△AEF==,
∴EH===4,
∴△AEF中AF边上的高的长度为4.
21世纪教育网(www.21cnjy.com)
第十七章勾股定理章节期中练习人教版2024—2025学年八年级下册
一、选择题
1.以下列各组数为边长的三角形中,是直角三角形的是( )
A.0.3,0.4,0.5 B.5,6,11
C.2,, D.4,5,6
2.满足下列条件的△ABC,不是直角三角形的为( )
A.∠A=∠B﹣∠C B.∠A:∠B:∠C=1:1:2
C.b2=a2﹣c2 D.a:b:c=2:3:4
3.如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D.2.5
4.在△ABC中,AB=12,BC=16,AC=20,则△ABC的面积是( )
A.120 B.160 C.216 D.96
5.丽丽想知道学校旗杆的高,她发现旗杆顶端上的绳子垂直到地面还多2米,当她把绳子的下端拉开离旗杆6米后,发现下端刚好接触地面,则旗杆的高为( )
A.4米 B.8米 C.10米 D.12米
6.如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=16.则S3=( )
A.20 B.12 C.2 D.2
7.在Rt△ABC中,∠C=90°,AC=2,BC=4,则点C到斜边AB的距离是( )
A. B.2 C. D.
8.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长是( )
A.3cm B.4cm C.5cm D.6cm
二、填空题
9.如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形ABC中,AC=17,BC=15,则阴影部分的面积是 .
10.若三角形的两边长为4和5,要使其成为直角三角形,则第三边的长为 .
11.如图,长方形纸片ABCD中,AB=4,BC=6,点E在AB边上,将纸片沿CE折叠,点B落在点F处,EF,CF分别交AD于点G,H,且EG=GH,则AE的长为 .
12.如图,有一圆柱,其高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为 cm.(π取3)
13.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.下图是3世纪我国汉代的数学家赵爽在注解《周髀算经》时给出的图案,人们称它为“赵爽弦图”.此图中四个全等的直角三角形可以围成一个大正方形,中空的部分是一个小正方形.如果大正方形的面积是25,小正方形的面积是1,则(a+b)2的值是 .
三、解答题
14.如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,CD′交AB于点F,求重叠部分△AFC的面积.
15.拖拉机行驶过程中会对周围产生较大的噪声影响.如图.有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域.
(1)求∠ACB度数;
(2)学校C会受噪声影响吗?为什么?
(3)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
16.如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
17.如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
18.已知:在四边形ABCD中,连接AC,BC=AB,CD2+AD2=2AB2,AD⊥CD.
(1)试判断AB与BC的位置关系,并说明理由;
(2)当,AD=17,求四边形ABCD的周长.
19.如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求:
(1)DE的长;
(2)求阴影部分△GED的面积.
20.如图,在正方形ABCD中,AB=8,BE=4,CF=2.
(1)判断△AEF的形状;
(2)求△AEF中AF边上的高的长度.
参考答案
一、选择题
1.【解答】解:A、∵0.32+0.42=0.52,
∴能构成直角三角形;符合题意;
B、∵52+62=61≠112,
∴不能构成直角三角形;不符合题意;
C、∵22+()2=9≠()2,
∴不能构成直角三角形;不符合题意;
D、∵42+52=41≠62,
∴不能构成直角三角形.不符合题意;
故选:A.
2.【解答】解:A、∠A=∠B﹣∠C,△ABC是直角三角形;
B、∠A:∠B:∠C=1:1:2,△ABC是直角三角形;
C、b2=a2﹣c2得b2+c2=a2,△ABC是直角三角形;
D:a:b:c=2:3:4,a=2x,那么b=3x,c=4x,a2+b2=13x2,c2=16x2,可证△ABC 不是直角三角形;
故选:D.
3.【解答】解:∵四边形OABC是矩形,
∴∠OAB=90°,
∴OB===,
∴这个点表示的示数是,
故选:C.
4.【解答】解:∵122+162=202,即AC2=AB2+BC2,
∴△ABC是直角三角形,且AC是直角边,
∴△ABC的面积是×12×16=96.
故选:D.
5.【解答】解:设旗杆的高为xm,则绳子的长为(x+2)m.
根据题意得:
x2+62=(x+2)2,
解得x=8.
故旗杆的高为8米.
故选:B.
6.【解答】解:∵∠ACB=90°,
∴BC2+AC2=AB2,
即4+16=20=AB2,
∴S3=20,
故选:A.
7.【解答】解:设点C到斜边AB的距离是h,
在Rt△ABC中,∠C=90°,AC=2,BC=4,
则由勾股定理,得AB==2,
由AC BC=AB h得到:h===.
故选:D.
8.【解答】解:∵四边形MNEF是由四边形ADMN折叠而成的,
∴DN=NE.
∵E是BC的中点且BC=8cm,
∴EC=4cm.
∵四边形ABCD是正方形,
∴∠BCD=90°.
设CN的长度为x cm,则EN=DN=(8﹣x)cm,
由勾股定理NC2+EC2=NE2,得x2+42=(8﹣x)2,
解得x=3.
故选:A.
二、填空题
9.【解答】解:由勾股定理得,AB2=AC2﹣BC2=172﹣152=64,
∵四边形ABFD为正方形,
∴DF=AB,
∴阴影部分的面积=DE2+EF2=DF2=64,
故答案为:64.
10.【解答】解:当4和5为直角边时,
第三边长为=;
当5为斜边,4为直角边时,
第三边长为=3.
故答案为:3或.
11.【解答】解:由题意可知,∠A=∠D=90°,AB=CD=4,AD=BC=6,
∵将△CBE沿CE翻折至△CFE,
∴∠F=∠B=∠A=90°,BE=EF,
又∵EG=GH,∠AGE=∠FGH,
∴△AGE≌△FGH(AAS),
∴FH=AE,GF=AG,
∴AH=BE=EF,
设AE=FH=x,则AH=BE=EF=4﹣x,
∴DH=AD﹣AH=x+2,CH=CF﹣FH=6﹣x,
∵CD2+DH2=CH2,
∴42+(2+x)2=(6﹣x)2,
解得:x=1,
∴AE=1,
故答案为:1.
12.【解答】解:圆柱展开图为长方形,
则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πrcm,
蚂蚁经过的最短距离为连接A,B的线段长,
由勾股定理得AB====15cm.
故蚂蚁经过的最短距离为15cm.
13.【解答】解:由图可得,
a2+b2=c2,c2=25,
∴a2+b2=25,
∵小正方形的面积是1,
∴(a﹣b)2=1,
∴a2﹣2ab+b2=1,
∴ab=12,
∴(a+b)2
=a2+2ab+b2
=(a2+b2)+2ab
=25+2×12
=25+24
=49,
故答案为:49.
三、解答题
14.【解答】解:由折叠和矩形的性质可知,∠D'=∠D=∠B=90°,AD'=CB=4,
又∵∠AFD'=∠CFB,
∴△AD'F≌△CBF(AAS),
∴AF=CF,
设BF=x,则AF=CF=8﹣x,
在Rt△CBF中,由勾股定理,得:x2+42=(8﹣x)2,
解得:x=3,
∴;
故重叠部分△AFC的面积为10.
15.【解答】解:(1)∵AC=150m,BC=200m,AB=250m,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°;
(2)学校C会受噪声影响.
理由:如图,过点C作CD⊥AB于D,
∴AC×BC=CD×AB,
∴150×200=250×CD,
∴CD==120(m),
∵拖拉机周围130m以内为受噪声影响区域,
∴学校C会受噪声影响.
(2)当EC=130m,FC=130m时,正好影响C学校,
∵ED=(m),
∴EF=100(m),
∵拖拉机的行驶速度为每分钟50米,
∴100÷50=2(分钟),
即拖拉机噪声影响该学校持续的时间有2分钟.
16.【解答】解:依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE===6,
∴CE=4,
∴E(4,8).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(8﹣OD)2+42=OD2,
∴OD=5,
∴D(0,5),
综上D点坐标为(0,5)、E点坐标为(4,8).
17.【解答】解:(1)由题意知,AB=(x+10)米,
在Rt△AOB中,由勾股定理得,
OB2+OA2=AB2,
即x2+202=(x+10)2,
解得x=15,
∴OB的长度为15米;
(2)由题意知,OC=AO﹣AC=20﹣5=15(米),CD=AB=25米,
在Rt△OCD中,由勾股定理得,
OC2+OD2=CD2,
即152+OD2=252,
解得OD=20米(负值舍去),
∴BD=20﹣15=5(米),
∴云梯的底部B往外移动了5米.
18.【解答】解:(1)AB⊥BC,理由如下:
∵AD⊥CD,
∴AD2+CD2=AC2,
∵CD2+AD2=2AB2,
∴AC2=2AB2,
∵BC=AB,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,且∠ABC=90°,
∴AB⊥BC;
(2)由(1)可知,∠ABC=90°,AD⊥CD,
∴CD2+AD2=AB2+BC2,
∵,AD=17,
∴CD2+172=(3CD)2+(3CD)2,
解得:,
∴,
∴四边形ABCD的周长=.
19.【解答】解:(1)设DE=EG=x,则AE=8﹣x,
在Rt△AEG中,AG2+EG2=AE2,
∴16+x2=(8﹣x)2,
解得x=3,
∴DE=3.
(2)过G点作GM⊥AD于M,
则 AG×GE= AE×GM,AG=AB=4,AE=CF=5,GE=DE=3,
∴GM=,
∴S△GED=GM×DE=.
20.【解答】解:(1)△AEF是直角三角形,理由如下:
∵四边形ABCD是正方形,AB=8,BE=4,CF=2.
∴EC=4,DF=6,
根据勾股定理可得:AE==4,
同理可得:EF=2,AF=10,
∴EF2+AE2=AF2,
∴△AEF是直角三角形;
(2)如图,过点E作EH⊥AF交AF于点H,
∵△AEF是直角三角形,
∴S△AEF==,
∴EH===4,
∴△AEF中AF边上的高的长度为4.
21世纪教育网(www.21cnjy.com)
同课章节目录
