第一章相交线与平行线章节期中复习(含解析)
文档属性
| 名称 | 第一章相交线与平行线章节期中复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1020.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一章相交线与平行线章节期中复习浙教版2024—2025学年七年级下册
一、选择题
1.下列图形中,由∠1=∠2,能得到AB∥CD的是( )
A. B. C. D.
2.如图,点E在BA的延长线上,能证明BE∥CD是( )
A.∠EAD=∠B B.∠BAD=∠ACD
C.∠EAD=∠ACD D.∠EAC+∠ACD=180°
3.下列汽车商标图案中,可以由一个“基本图案”通过连续平移得到的是( )
A. B. C. D.
4.如图,小明到小颖家有四条路,小明想尽快到达小颖家,他选择走第②条路,其中的道理是( )
A.直线外一点与直线上点之间的连线段有无数条
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间线段最短
5.如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=( )
A.130° B.150° C.120° D.140°
6.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有( )个交点.
A.24 B.26 C.28 D.30
7.如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=3,平移距离为6,则阴影部分面积为( )
A.48 B.51 C.64 D.42
8.如图a是长方形纸带,∠DEF=23°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.97° B.105° C.107° D.111°
9.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130°
B.第一次左拐50°,第二次右拐130°
C.第一次左拐50°,第二次左拐130°
D.第一次右拐50°,第二次左拐50°
10.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是( )
A.x﹣z=y B.x+y+z=180°
C.y﹣x=z D.y﹣x=x﹣z
二、填空题
11.如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是 .
12.如图,将△ABC沿直线BD方向向右平移,得到△ECD,若BD=24,则AE= .
13.如图,直线a,b相交,如果∠3=40°,那么∠1+∠2= .
14.如图,∠B+∠DCB=180°,AC平分∠DAB,若∠BAC=50°,则∠D= 80 度.
15.如图,在四边形ABCD纸片中,AD∥BC,AB∥CD.将纸片折叠,点A、B分别落在G、H处,EF为折痕,FH交CD于点K.若∠CKF=40°,则 .
16.①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠E=∠A+∠C;③如图3,若AB∥EF,则∠x=180°﹣∠α﹣∠γ+∠β;④如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的是 .
三、解答题
17.已知:如图,AB∥CD,DB⊥BC,∠1=35°.求∠2的度数.
18.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的5倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
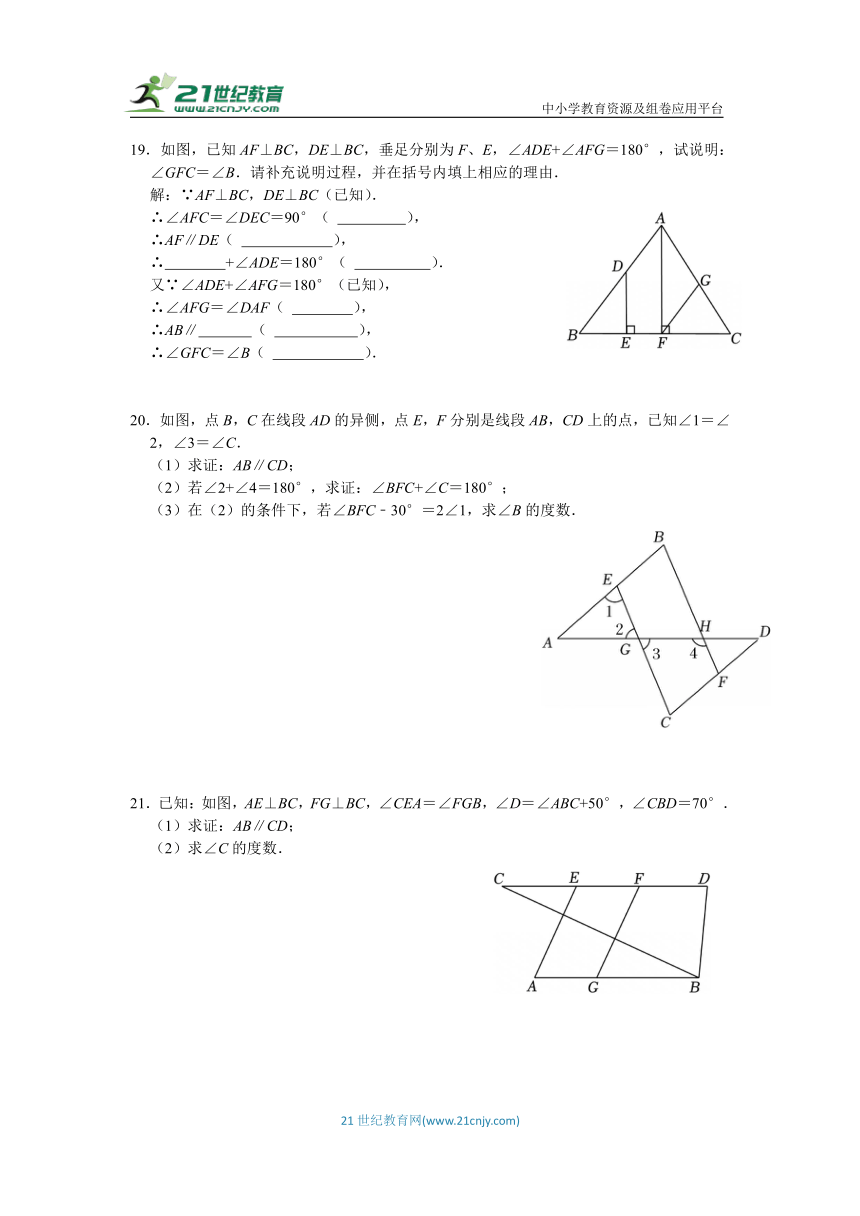
19.如图,已知AF⊥BC,DE⊥BC,垂足分别为F、E,∠ADE+∠AFG=180°,试说明:∠GFC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AF⊥BC,DE⊥BC(已知).
∴∠AFC=∠DEC=90°( ),
∴AF∥DE( ),
∴ +∠ADE=180°( ).
又∵∠ADE+∠AFG=180°(已知),
∴∠AFG=∠DAF( ),
∴AB∥ ( ),
∴∠GFC=∠B( ).
20.如图,点B,C在线段AD的异侧,点E,F分别是线段AB,CD上的点,已知∠1=∠2,∠3=∠C.
(1)求证:AB∥CD;
(2)若∠2+∠4=180°,求证:∠BFC+∠C=180°;
(3)在(2)的条件下,若∠BFC﹣30°=2∠1,求∠B的度数.
21.已知:如图,AE⊥BC,FG⊥BC,∠CEA=∠FGB,∠D=∠ABC+50°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
22.如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣8|+(b﹣2)2=0.
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动15秒,射线BQ才开始绕点B逆时针旋转,在射线BQ第一次到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?
23.已知AB∥CD,直线MN交AB、CD于点M、N.
(1)如图1所示,点E在线段MN上,设∠MBE=x°,∠MND=y°,且满足,则x= ,y= ;∠MEB= .
(2)如图2所示,点E在线段MN上,∠MBE=∠MEB,DF平分∠EDC,交BE的延长线于点F,试找出∠DEF、∠END、∠EDN之间的数量关系,并证明;
(3)如图3所示,点P在射线NT上运动时,∠PCD的角平分线与∠TMB的角平分线交于点Q,求的值.
24.已知:AB∥CD,点E在直线AB、CD之间,连接EA、EC.
(1)如图1,若∠A=80°,∠C=50°,求∠AEC的度数;
(2)如图2,若AF平分∠BAE,CF平分∠DCE交AF于点F,直接写出∠AEC和∠AFC之间的数量关系∠AEC= ;
(3)如图3,在(2)的条件下,延长AE交DC于点G,在AG上取一点K,连接FK交CD于点H,CL⊥AF,若∠CEG=50°,∠AFK=∠CHF.求∠GKH.
参考答案
一、选择题
1.【解答】解:A、由∠1=∠2,不能得到AB∥CD,故不符合题意;
B、∵∠1=∠2,∴AC∥BD,不能得到AB∥CD,故不符合题意;
C、由∠1=∠2,不能得到AB∥CD,故不符合题意;
D、∵∠1=∠2,∴AB∥CD,故符合题意;
故选:D.
2.【解答】解:A、若∠EAD=∠B,则AD∥BC,故此选项错误;
B、若∠BAD=∠ACD,不可能得到BE∥CD,故此选项错误;
C、若∠EAD=∠ACD,不能得到BE∥CD,故此选项错误;
D、若∠EAC+∠ACD=180°,则BE∥CD,故此选项正确.
故选:D.
3.【解答】解:A、可以由一个“基本图案”旋转得到,故本选项错误;
B、是轴对称图形,不是基本图案的组合图形,故本选项错误;
C、是轴对称图形,不是基本图案的组合图形,故本选项错误;
D、可以由一个“基本图案”平移得到,故把本选项正确.
故选:D.
4.【解答】解:小明想尽快到达小颖家,他选择走第②条路,其中的道理是两点之间线段最短.
故选:D.
5.【解答】解:∵∠COE为直角,∠AOE=60°,
∴∠DOE=180°﹣∠COE=180°﹣90°=90°,
∴∠AOD=∠DOE﹣∠AOE=90°﹣60°=30°,
∴∠BOD=180°﹣∠AOD=180°﹣30°=150°.
故选:B.
6.【解答】解:∵3条直线两两相交,最多有个交点,
4条直线两两相交,最多有个交点,
5条直线两两相交,最多有个交点,
∴n条直线两两相交,最多有个交点,
∴8条直线两两相交,最多有个交点,
故选:C.
7.【解答】解:由题意可得S△ABC=S△DEF,故阴影部分的面积=S△ABC﹣S△OEC=S梯形ABEO,
∵平移距离为6,
∴BE=6,OE=DE﹣DO=AB﹣DO=7,
∴阴影部分的面积,
故选:B.
8.【解答】解:由长方形纸带可得AD∥BC,
∴图a中∠EFB=∠DEF=23°,
根据翻折的性质,可得到图b中∠FEG=23°,
∴∠FGD=180°﹣∠EGF=∠GEF+∠GFE=46°,
∵CD∥FC,
∴∠GFC=180°﹣∠FGD=134°,
根据翻折的性质,可得图c中∠CFG=134°,
∴∠EFC=∠GFC﹣∠EFG=134°﹣23°=111°,
故选:D.
9.【解答】解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,也可以得到∠1=∠2.
故选:D.
10.【解答】解:如图所示,延长AB交DE于H,
∵BC∥DE,
∴∠ABC=∠AHE=x,
∵CD∥EF,AB∥EG,
∴∠D=∠DEF=z,∠AHE=∠DEG=z+y,
∴∠ABC=∠DEG,
即x=z+y,
∴x﹣z=y.
故选:A.
二、填空题
11.【解答】解:∵AB∥CD,∠B=26°,
∴∠BCD=∠B=26°,
∵CB平分∠ECD,
∴∠ECD=2∠BCD=52°,
∵AB∥CD,
∴∠1=∠ECD=52°,
故答案为:52°.
12.【解答】解:∵△ABC沿直线BD方向向右平移,得到△ECD,
∴,
∵BD=24
∴AE=12,
故答案为:12.
13.【解答】解:∵∠3=40°,
∴∠1=180°﹣40°=140°,
∴∠1=∠2=140°,
∴∠1+∠2=140°+140°=280°,
故答案为:280°.
14.【解答】解:∵∠B+∠DCB=180°,
∴AB∥CD.
∴∠D+∠DAB=180°.
∵AC平分∠DAB,∠BAC=50°,
∴∠DAB=2∠BAC=100°,
∴∠D=180°﹣100°=80°.
故答案为:80.
15.【解答】解:∵AD∥BC,AB∥CD,
∴∠A+∠B=180°,∠C+∠B=180°,
∴∠A=∠C,
根据翻转折叠的性质可知,∠AEF=∠GEF,∠EFB=∠EFK,
∵AD∥BC,
∴∠DEF=∠EFB,∠AEF=∠EFC,
∴∠GEF=∠AEF=∠EFC,∠DEF=∠EFB=∠EFK,
∴∠GEF﹣∠DEF=∠EFC﹣∠EFK,
∴∠GED=∠CFK,
∵∠C+∠CFK+∠CKF=180°,
∴∠C+∠CFK=140°,
∴∠A+∠GED=140°,
则,
故答案为:110.
16.【解答】解:①如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;
②如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠A+∠C=∠CEF+∠AEF=∠AEC,则②正确;
③如图3,过点C作CD∥AB,延长AB到G,
∵AB∥EF,
∴AB∥EF∥CD,
∴∠DCF=∠EFC,
由②的结论可知∠GBH+∠HCD=∠BHC,
又∵∠GBH=180°﹣∠ABH,∠HCD=∠HCF﹣∠DCF
∴180°﹣∠ABH+∠HCF﹣∠DCF=∠BHC,
∴180°﹣∠ABH+∠HCF﹣∠EFC=∠BHC,
∴180°﹣∠α+∠β﹣∠γ=∠x,故③正确;
④如图4,
过点P作PF∥AB,
∵AB∥CD,
∴AB∥PF∥CD,
∴∠A=∠APF,∠C=∠CPF,
∴∠A=∠CPF+∠APC=∠C+∠APC,则④正确;
故答案为:②③④.
三、解答题
17.【解答】解:∵AB∥CD,
∴∠EBD=∠2,
∵DB⊥BC,
∴∠1+∠EBD=∠1+∠2=90°,
∵∠1=35°,
∴∠2=90°﹣∠1=55°.
18.【解答】解:(1)∵AB是直线(已知),
∴∠BOD+∠AOD=180°,
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD180°=30°,∠BOD180°=150°.
(2)∵∠BOC=∠AOD=30°,OE⊥DC,
∴∠EOC=90°,
∴∠BOE=∠EOC﹣∠BOC=90°﹣30°=60°.
19.解:∵AF⊥BC,DE⊥BC(已知).
∴∠AFC=∠DEC=90°( 垂线的定义 ),
∴AF∥DE( 同位角相等,两直线平行 ),
∴ ∠DAF +∠ADE=180°( 两直线平行,同旁内角互补 ).
又∵∠ADE+∠AFG=180°(已知),
∴∠AFG=∠DAF( 等量代换 ),
∴AB∥ GF ( 内错角相等,两直线平行 ),
∴∠GFC=∠B( 两直线平行,同位角相等 ).
20.【解答】(1)证明:∵∠1=∠2,∠3=∠C,∠2=∠3,
∴∠1=∠C,
∴AB∥CD;
(2)证明:∵∠2+∠4=180°,∠2=∠3,
∴∠3+∠4=180°,
∴BF∥EC,
∴∠BFC+∠C=180°;
(3)解:∵∠BFC+∠C=180°,
∵∠BFC﹣30°=2∠1=2∠C,
∴∠BFC=2∠C+30°,
∴2∠C+30°+∠C=180°,
∴∠C=50°,
∴∠BFC=130°,
∵AB∥CD,
∴∠B+∠BFC=180°,
∴∠B=50°.
21.【解答】(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠EAB=∠FGB,
∵∠CEA=∠FGB,
∴∠CEA=∠EAB,
∴AB∥CD;
(2)解:由(1)得,AB∥CD,
∴∠D+∠CBD+∠ABC=180°,
∵∠D=∠ABC+50°,∠CBD=70°,
∴∠ABC+70°+∠ABC+50°=180°,
∴∠ABC=30°,
∴∠C=∠ABC=30°.
22.【解答】解:(1)∵|a﹣8|+(b﹣2)2=0,|a﹣8|≥0,(b﹣2)2≥0,
∴a﹣8=0,b﹣2=0,
∴a=8,b=2,
故答案为:8;2;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直,
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=180°﹣(∠ABO+∠BAO)=180°﹣90°=90°,
又∵∠OBQ=2t°,∠OAM=8t°,
∴2t+8t=90,
∴10t=90,
∴t=9,
∴至少旋转9秒时,射线AM、射线BQ互相垂直;
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动15秒后,AM转动至AM′的位置,则∠MAM′=15×8=120°,
∴∠M′AB=180°﹣45°﹣120°=15°;
分两种情况:
①当时,∠QBQ′=2t°,∠M′AM″=8t°,
∵PQ∥MN,
∴∠BAN=45°=∠ABQ,
∴∠ABQ′=45°﹣2t°,∠BAM″=∠M′AM″﹣∠M′AB=8t°﹣15°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
∴45﹣2t=8t﹣15,
∴10t=60,
解得t=6;
②当7.5<t<13.125时,∠QBQ′=2t°,∠NAM″=8(t﹣7.5)°=8t°﹣60°,
∴∠ABQ′=45°﹣2t°,∠BAM″=45°﹣(8t°﹣60°)=105°﹣8t°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
此时,45﹣2t=105﹣8t,
∴6t=60,
解得t=10;
综上所述,射线AM再转动6秒或10秒时,射线AM、射线BQ互相平行.
23.【解答】解:(1)如图所示,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠MEF=∠MND=y°,∠BEF=∠MBE=x°,
∴∠MEB=∠MEF﹣∠MBE=y°﹣x°,
∵,,
∴,
∴x﹣10=0,y﹣60=0,
∴x=10,y=60,
∴∠MEB=y°﹣x°=60°﹣10°=50°;
故答案为:10,60,50°;
(2),证明如下:
如图所示,过点E作EG∥AB,
∵AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠MEG=∠END,
∵∠MBE=∠MEB,∠FEN=∠MEB,
∴∠MBE=∠BEG=∠FEN=∠MEB,
∴;
在△EDN中,∠EDN+∠END+∠DEN=180°,
∴∠EDN+∠END+∠DEF﹣∠FEN=180°,
∴,
∴;
(3)如图所示,设CD、MQ交于I,CQ、PM交于K,过点K作KH∥AB交MQ于H,
∵AB∥CD,
∴∠BMN=∠MNC,
∵∠MNC+∠CNP=180°=∠NCP+CPN+∠CNP,
∴∠CPM=∠BMN﹣∠NCP;
∵MQ平分∠TMB,
∴∠BMI=∠IMN,
∵AB∥CD,KH∥AB,
∴∠NMI=∠NIM=∠IHK,∠NCK=∠HKQ;
∵CQ平分∠PCN,
∴,
同理可得∠Q=∠IHK﹣∠HKQ,
∴,
∴.
24.【解答】解:(1)如图,过点E作EG∥AB,
∴∠GEA=∠A,∠GEC=∠C,
∵∠A=80°,∠C=50°,
∴∠GEA=80°,∠GEC=50°,
∴∠AEC=∠GEA+∠GEC=130°;
(2)过点E作EG∥AB,
∴∠GEA=∠BAE,∠GEC=∠ECD,
∴∠AEC=∠GEA+∠GEC=∠BAE+∠DCE,
同理∠F=∠FAB+∠FCD,
由题意可得:
,,
∴,
∴∠AEC=2∠AFC,
故答案为:∠AFC;
(3)∵∠CEG=50°,
∴∠AEC=130°,
∵,
又CL⊥AF,
∴∠CLF=90°,
∴∠LCF=25°,
∴设∠CFK=α,∠K=β,∠BAF=∠EAF=x,∠ECF=∠FCD=y,则∠AFK=∠CHF=65°+α,
根据三角形的内角和为180度可得:
∠FCH+∠CFH+∠CHF=180°,
∴x+α+α+65°=180°,
∴x+2α=115°,
由(2)知:∠AFC=∠BAF+∠FCD,
∴x+y=65°,
∵∠AOF=∠OFK+∠K,
∴α+β=25°+50°=75°,
∴α+β+x+y=140°,
∵∠AFK=∠CHF,
∴∠FAK+∠K=∠FCH+∠CFH,即α+x=β+y,
∴α+x=70°,
把α+x=70°代入x+2α=115°,得70°+α=115°,
∴α=45°,∴∠K=β=30°.
21世纪教育网(www.21cnjy.com)
第一章相交线与平行线章节期中复习浙教版2024—2025学年七年级下册
一、选择题
1.下列图形中,由∠1=∠2,能得到AB∥CD的是( )
A. B. C. D.
2.如图,点E在BA的延长线上,能证明BE∥CD是( )
A.∠EAD=∠B B.∠BAD=∠ACD
C.∠EAD=∠ACD D.∠EAC+∠ACD=180°
3.下列汽车商标图案中,可以由一个“基本图案”通过连续平移得到的是( )
A. B. C. D.
4.如图,小明到小颖家有四条路,小明想尽快到达小颖家,他选择走第②条路,其中的道理是( )
A.直线外一点与直线上点之间的连线段有无数条
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间线段最短
5.如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=( )
A.130° B.150° C.120° D.140°
6.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有( )个交点.
A.24 B.26 C.28 D.30
7.如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=3,平移距离为6,则阴影部分面积为( )
A.48 B.51 C.64 D.42
8.如图a是长方形纸带,∠DEF=23°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.97° B.105° C.107° D.111°
9.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130°
B.第一次左拐50°,第二次右拐130°
C.第一次左拐50°,第二次左拐130°
D.第一次右拐50°,第二次左拐50°
10.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是( )
A.x﹣z=y B.x+y+z=180°
C.y﹣x=z D.y﹣x=x﹣z
二、填空题
11.如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是 .
12.如图,将△ABC沿直线BD方向向右平移,得到△ECD,若BD=24,则AE= .
13.如图,直线a,b相交,如果∠3=40°,那么∠1+∠2= .
14.如图,∠B+∠DCB=180°,AC平分∠DAB,若∠BAC=50°,则∠D= 80 度.
15.如图,在四边形ABCD纸片中,AD∥BC,AB∥CD.将纸片折叠,点A、B分别落在G、H处,EF为折痕,FH交CD于点K.若∠CKF=40°,则 .
16.①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠E=∠A+∠C;③如图3,若AB∥EF,则∠x=180°﹣∠α﹣∠γ+∠β;④如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的是 .
三、解答题
17.已知:如图,AB∥CD,DB⊥BC,∠1=35°.求∠2的度数.
18.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的5倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
19.如图,已知AF⊥BC,DE⊥BC,垂足分别为F、E,∠ADE+∠AFG=180°,试说明:∠GFC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AF⊥BC,DE⊥BC(已知).
∴∠AFC=∠DEC=90°( ),
∴AF∥DE( ),
∴ +∠ADE=180°( ).
又∵∠ADE+∠AFG=180°(已知),
∴∠AFG=∠DAF( ),
∴AB∥ ( ),
∴∠GFC=∠B( ).
20.如图,点B,C在线段AD的异侧,点E,F分别是线段AB,CD上的点,已知∠1=∠2,∠3=∠C.
(1)求证:AB∥CD;
(2)若∠2+∠4=180°,求证:∠BFC+∠C=180°;
(3)在(2)的条件下,若∠BFC﹣30°=2∠1,求∠B的度数.
21.已知:如图,AE⊥BC,FG⊥BC,∠CEA=∠FGB,∠D=∠ABC+50°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
22.如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣8|+(b﹣2)2=0.
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动15秒,射线BQ才开始绕点B逆时针旋转,在射线BQ第一次到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?
23.已知AB∥CD,直线MN交AB、CD于点M、N.
(1)如图1所示,点E在线段MN上,设∠MBE=x°,∠MND=y°,且满足,则x= ,y= ;∠MEB= .
(2)如图2所示,点E在线段MN上,∠MBE=∠MEB,DF平分∠EDC,交BE的延长线于点F,试找出∠DEF、∠END、∠EDN之间的数量关系,并证明;
(3)如图3所示,点P在射线NT上运动时,∠PCD的角平分线与∠TMB的角平分线交于点Q,求的值.
24.已知:AB∥CD,点E在直线AB、CD之间,连接EA、EC.
(1)如图1,若∠A=80°,∠C=50°,求∠AEC的度数;
(2)如图2,若AF平分∠BAE,CF平分∠DCE交AF于点F,直接写出∠AEC和∠AFC之间的数量关系∠AEC= ;
(3)如图3,在(2)的条件下,延长AE交DC于点G,在AG上取一点K,连接FK交CD于点H,CL⊥AF,若∠CEG=50°,∠AFK=∠CHF.求∠GKH.
参考答案
一、选择题
1.【解答】解:A、由∠1=∠2,不能得到AB∥CD,故不符合题意;
B、∵∠1=∠2,∴AC∥BD,不能得到AB∥CD,故不符合题意;
C、由∠1=∠2,不能得到AB∥CD,故不符合题意;
D、∵∠1=∠2,∴AB∥CD,故符合题意;
故选:D.
2.【解答】解:A、若∠EAD=∠B,则AD∥BC,故此选项错误;
B、若∠BAD=∠ACD,不可能得到BE∥CD,故此选项错误;
C、若∠EAD=∠ACD,不能得到BE∥CD,故此选项错误;
D、若∠EAC+∠ACD=180°,则BE∥CD,故此选项正确.
故选:D.
3.【解答】解:A、可以由一个“基本图案”旋转得到,故本选项错误;
B、是轴对称图形,不是基本图案的组合图形,故本选项错误;
C、是轴对称图形,不是基本图案的组合图形,故本选项错误;
D、可以由一个“基本图案”平移得到,故把本选项正确.
故选:D.
4.【解答】解:小明想尽快到达小颖家,他选择走第②条路,其中的道理是两点之间线段最短.
故选:D.
5.【解答】解:∵∠COE为直角,∠AOE=60°,
∴∠DOE=180°﹣∠COE=180°﹣90°=90°,
∴∠AOD=∠DOE﹣∠AOE=90°﹣60°=30°,
∴∠BOD=180°﹣∠AOD=180°﹣30°=150°.
故选:B.
6.【解答】解:∵3条直线两两相交,最多有个交点,
4条直线两两相交,最多有个交点,
5条直线两两相交,最多有个交点,
∴n条直线两两相交,最多有个交点,
∴8条直线两两相交,最多有个交点,
故选:C.
7.【解答】解:由题意可得S△ABC=S△DEF,故阴影部分的面积=S△ABC﹣S△OEC=S梯形ABEO,
∵平移距离为6,
∴BE=6,OE=DE﹣DO=AB﹣DO=7,
∴阴影部分的面积,
故选:B.
8.【解答】解:由长方形纸带可得AD∥BC,
∴图a中∠EFB=∠DEF=23°,
根据翻折的性质,可得到图b中∠FEG=23°,
∴∠FGD=180°﹣∠EGF=∠GEF+∠GFE=46°,
∵CD∥FC,
∴∠GFC=180°﹣∠FGD=134°,
根据翻折的性质,可得图c中∠CFG=134°,
∴∠EFC=∠GFC﹣∠EFG=134°﹣23°=111°,
故选:D.
9.【解答】解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,也可以得到∠1=∠2.
故选:D.
10.【解答】解:如图所示,延长AB交DE于H,
∵BC∥DE,
∴∠ABC=∠AHE=x,
∵CD∥EF,AB∥EG,
∴∠D=∠DEF=z,∠AHE=∠DEG=z+y,
∴∠ABC=∠DEG,
即x=z+y,
∴x﹣z=y.
故选:A.
二、填空题
11.【解答】解:∵AB∥CD,∠B=26°,
∴∠BCD=∠B=26°,
∵CB平分∠ECD,
∴∠ECD=2∠BCD=52°,
∵AB∥CD,
∴∠1=∠ECD=52°,
故答案为:52°.
12.【解答】解:∵△ABC沿直线BD方向向右平移,得到△ECD,
∴,
∵BD=24
∴AE=12,
故答案为:12.
13.【解答】解:∵∠3=40°,
∴∠1=180°﹣40°=140°,
∴∠1=∠2=140°,
∴∠1+∠2=140°+140°=280°,
故答案为:280°.
14.【解答】解:∵∠B+∠DCB=180°,
∴AB∥CD.
∴∠D+∠DAB=180°.
∵AC平分∠DAB,∠BAC=50°,
∴∠DAB=2∠BAC=100°,
∴∠D=180°﹣100°=80°.
故答案为:80.
15.【解答】解:∵AD∥BC,AB∥CD,
∴∠A+∠B=180°,∠C+∠B=180°,
∴∠A=∠C,
根据翻转折叠的性质可知,∠AEF=∠GEF,∠EFB=∠EFK,
∵AD∥BC,
∴∠DEF=∠EFB,∠AEF=∠EFC,
∴∠GEF=∠AEF=∠EFC,∠DEF=∠EFB=∠EFK,
∴∠GEF﹣∠DEF=∠EFC﹣∠EFK,
∴∠GED=∠CFK,
∵∠C+∠CFK+∠CKF=180°,
∴∠C+∠CFK=140°,
∴∠A+∠GED=140°,
则,
故答案为:110.
16.【解答】解:①如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;
②如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠A+∠C=∠CEF+∠AEF=∠AEC,则②正确;
③如图3,过点C作CD∥AB,延长AB到G,
∵AB∥EF,
∴AB∥EF∥CD,
∴∠DCF=∠EFC,
由②的结论可知∠GBH+∠HCD=∠BHC,
又∵∠GBH=180°﹣∠ABH,∠HCD=∠HCF﹣∠DCF
∴180°﹣∠ABH+∠HCF﹣∠DCF=∠BHC,
∴180°﹣∠ABH+∠HCF﹣∠EFC=∠BHC,
∴180°﹣∠α+∠β﹣∠γ=∠x,故③正确;
④如图4,
过点P作PF∥AB,
∵AB∥CD,
∴AB∥PF∥CD,
∴∠A=∠APF,∠C=∠CPF,
∴∠A=∠CPF+∠APC=∠C+∠APC,则④正确;
故答案为:②③④.
三、解答题
17.【解答】解:∵AB∥CD,
∴∠EBD=∠2,
∵DB⊥BC,
∴∠1+∠EBD=∠1+∠2=90°,
∵∠1=35°,
∴∠2=90°﹣∠1=55°.
18.【解答】解:(1)∵AB是直线(已知),
∴∠BOD+∠AOD=180°,
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD180°=30°,∠BOD180°=150°.
(2)∵∠BOC=∠AOD=30°,OE⊥DC,
∴∠EOC=90°,
∴∠BOE=∠EOC﹣∠BOC=90°﹣30°=60°.
19.解:∵AF⊥BC,DE⊥BC(已知).
∴∠AFC=∠DEC=90°( 垂线的定义 ),
∴AF∥DE( 同位角相等,两直线平行 ),
∴ ∠DAF +∠ADE=180°( 两直线平行,同旁内角互补 ).
又∵∠ADE+∠AFG=180°(已知),
∴∠AFG=∠DAF( 等量代换 ),
∴AB∥ GF ( 内错角相等,两直线平行 ),
∴∠GFC=∠B( 两直线平行,同位角相等 ).
20.【解答】(1)证明:∵∠1=∠2,∠3=∠C,∠2=∠3,
∴∠1=∠C,
∴AB∥CD;
(2)证明:∵∠2+∠4=180°,∠2=∠3,
∴∠3+∠4=180°,
∴BF∥EC,
∴∠BFC+∠C=180°;
(3)解:∵∠BFC+∠C=180°,
∵∠BFC﹣30°=2∠1=2∠C,
∴∠BFC=2∠C+30°,
∴2∠C+30°+∠C=180°,
∴∠C=50°,
∴∠BFC=130°,
∵AB∥CD,
∴∠B+∠BFC=180°,
∴∠B=50°.
21.【解答】(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠EAB=∠FGB,
∵∠CEA=∠FGB,
∴∠CEA=∠EAB,
∴AB∥CD;
(2)解:由(1)得,AB∥CD,
∴∠D+∠CBD+∠ABC=180°,
∵∠D=∠ABC+50°,∠CBD=70°,
∴∠ABC+70°+∠ABC+50°=180°,
∴∠ABC=30°,
∴∠C=∠ABC=30°.
22.【解答】解:(1)∵|a﹣8|+(b﹣2)2=0,|a﹣8|≥0,(b﹣2)2≥0,
∴a﹣8=0,b﹣2=0,
∴a=8,b=2,
故答案为:8;2;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直,
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=180°﹣(∠ABO+∠BAO)=180°﹣90°=90°,
又∵∠OBQ=2t°,∠OAM=8t°,
∴2t+8t=90,
∴10t=90,
∴t=9,
∴至少旋转9秒时,射线AM、射线BQ互相垂直;
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动15秒后,AM转动至AM′的位置,则∠MAM′=15×8=120°,
∴∠M′AB=180°﹣45°﹣120°=15°;
分两种情况:
①当时,∠QBQ′=2t°,∠M′AM″=8t°,
∵PQ∥MN,
∴∠BAN=45°=∠ABQ,
∴∠ABQ′=45°﹣2t°,∠BAM″=∠M′AM″﹣∠M′AB=8t°﹣15°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
∴45﹣2t=8t﹣15,
∴10t=60,
解得t=6;
②当7.5<t<13.125时,∠QBQ′=2t°,∠NAM″=8(t﹣7.5)°=8t°﹣60°,
∴∠ABQ′=45°﹣2t°,∠BAM″=45°﹣(8t°﹣60°)=105°﹣8t°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
此时,45﹣2t=105﹣8t,
∴6t=60,
解得t=10;
综上所述,射线AM再转动6秒或10秒时,射线AM、射线BQ互相平行.
23.【解答】解:(1)如图所示,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠MEF=∠MND=y°,∠BEF=∠MBE=x°,
∴∠MEB=∠MEF﹣∠MBE=y°﹣x°,
∵,,
∴,
∴x﹣10=0,y﹣60=0,
∴x=10,y=60,
∴∠MEB=y°﹣x°=60°﹣10°=50°;
故答案为:10,60,50°;
(2),证明如下:
如图所示,过点E作EG∥AB,
∵AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠MEG=∠END,
∵∠MBE=∠MEB,∠FEN=∠MEB,
∴∠MBE=∠BEG=∠FEN=∠MEB,
∴;
在△EDN中,∠EDN+∠END+∠DEN=180°,
∴∠EDN+∠END+∠DEF﹣∠FEN=180°,
∴,
∴;
(3)如图所示,设CD、MQ交于I,CQ、PM交于K,过点K作KH∥AB交MQ于H,
∵AB∥CD,
∴∠BMN=∠MNC,
∵∠MNC+∠CNP=180°=∠NCP+CPN+∠CNP,
∴∠CPM=∠BMN﹣∠NCP;
∵MQ平分∠TMB,
∴∠BMI=∠IMN,
∵AB∥CD,KH∥AB,
∴∠NMI=∠NIM=∠IHK,∠NCK=∠HKQ;
∵CQ平分∠PCN,
∴,
同理可得∠Q=∠IHK﹣∠HKQ,
∴,
∴.
24.【解答】解:(1)如图,过点E作EG∥AB,
∴∠GEA=∠A,∠GEC=∠C,
∵∠A=80°,∠C=50°,
∴∠GEA=80°,∠GEC=50°,
∴∠AEC=∠GEA+∠GEC=130°;
(2)过点E作EG∥AB,
∴∠GEA=∠BAE,∠GEC=∠ECD,
∴∠AEC=∠GEA+∠GEC=∠BAE+∠DCE,
同理∠F=∠FAB+∠FCD,
由题意可得:
,,
∴,
∴∠AEC=2∠AFC,
故答案为:∠AFC;
(3)∵∠CEG=50°,
∴∠AEC=130°,
∵,
又CL⊥AF,
∴∠CLF=90°,
∴∠LCF=25°,
∴设∠CFK=α,∠K=β,∠BAF=∠EAF=x,∠ECF=∠FCD=y,则∠AFK=∠CHF=65°+α,
根据三角形的内角和为180度可得:
∠FCH+∠CFH+∠CHF=180°,
∴x+α+α+65°=180°,
∴x+2α=115°,
由(2)知:∠AFC=∠BAF+∠FCD,
∴x+y=65°,
∵∠AOF=∠OFK+∠K,
∴α+β=25°+50°=75°,
∴α+β+x+y=140°,
∵∠AFK=∠CHF,
∴∠FAK+∠K=∠FCH+∠CFH,即α+x=β+y,
∴α+x=70°,
把α+x=70°代入x+2α=115°,得70°+α=115°,
∴α=45°,∴∠K=β=30°.
21世纪教育网(www.21cnjy.com)
同课章节目录
