第十七章 勾股定理期中考试练习(含答案)人教版2024—2025学年八年级下册
文档属性
| 名称 | 第十七章 勾股定理期中考试练习(含答案)人教版2024—2025学年八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 480.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 14:55:16 | ||
图片预览



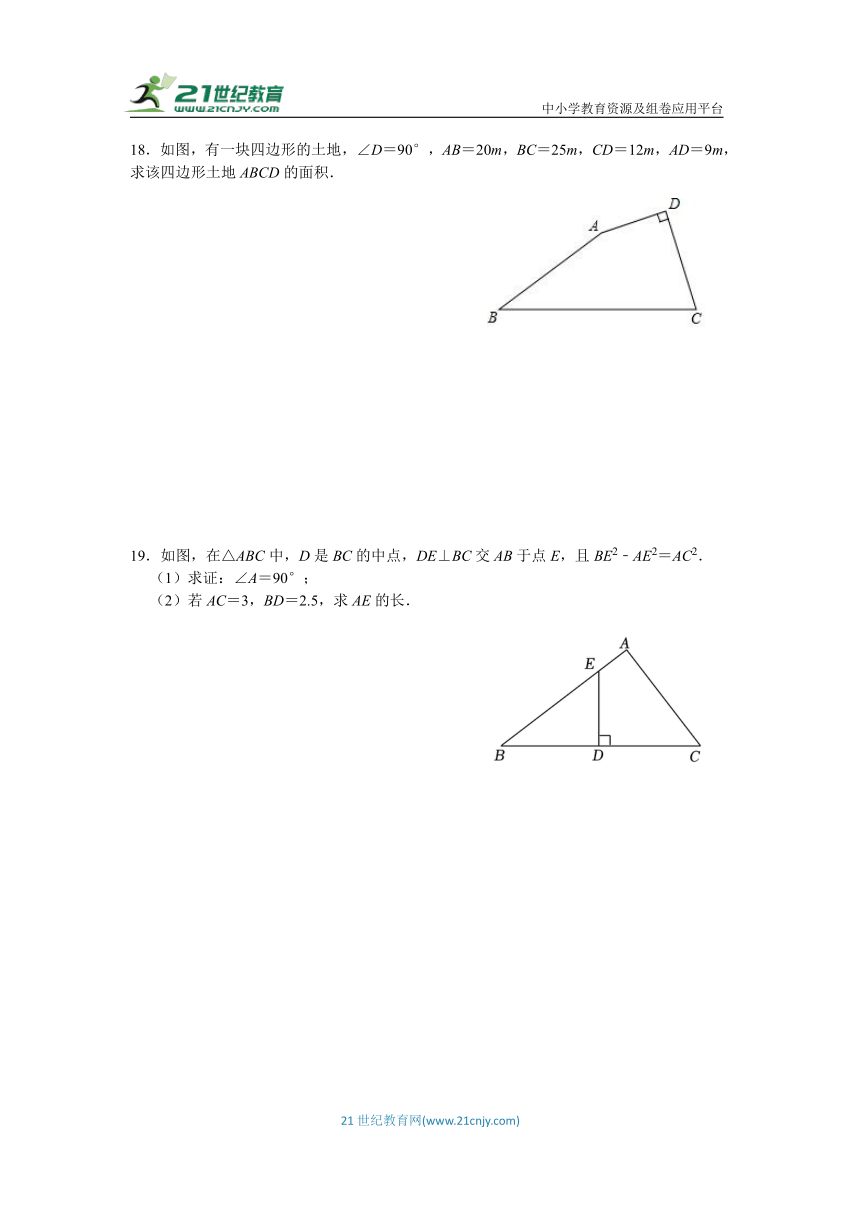
文档简介
中小学教育资源及组卷应用平台
第十七章勾股定理期中考试练习人教版2024—2025学年八年级下册
一、选择题
1.下列长度的三条线段能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.6,8,9
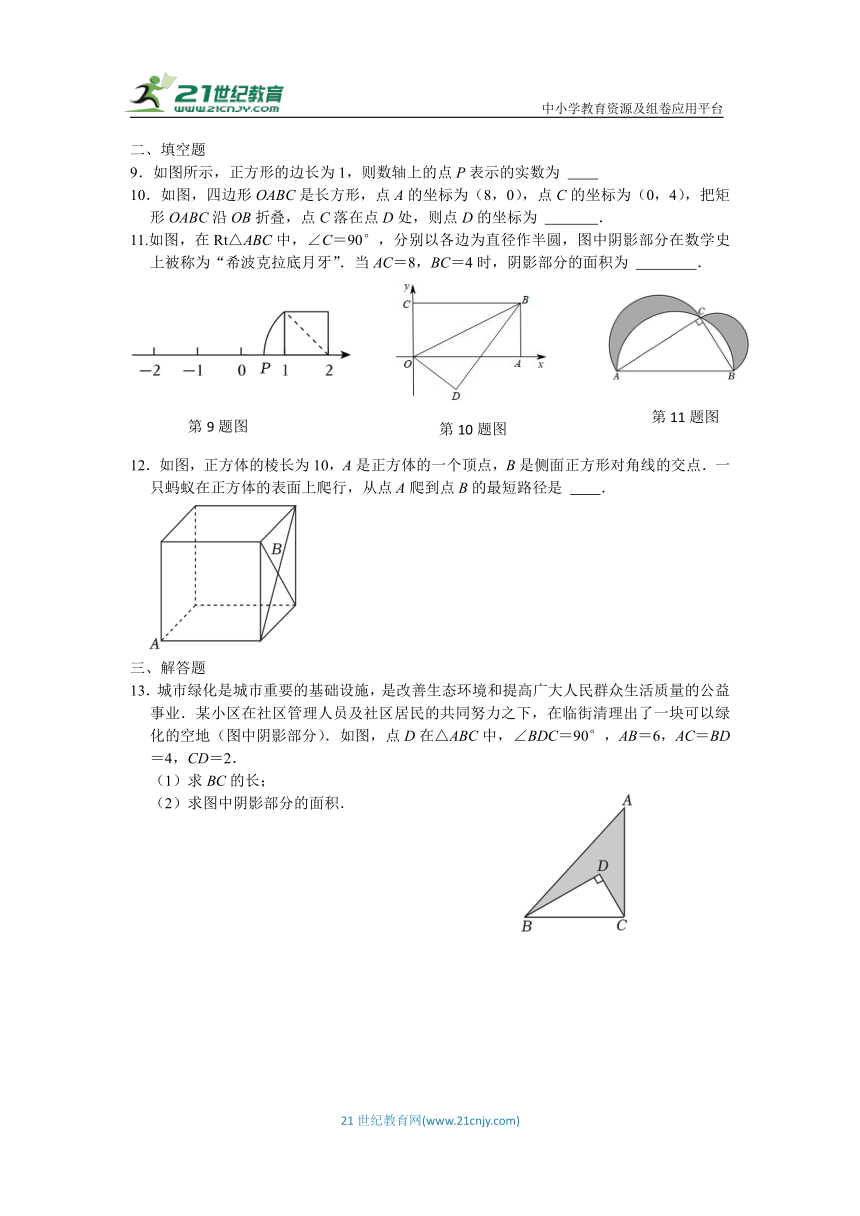
2.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行( )米.
A.7 B.8 C.9 D.10
3.下列四组长度的线段中,首尾相连后能构成直角三角形的是( )
A.a=2,b=2, B.a=2,b=3,c=4
C.a=1,, D.a=2,b=2,c=2
4.如图,在Rt△ABC中,AB=9,BC=6,∠ABC=90°.将△ABC折叠,使点A与BC的中点D重合,则BN的长是( )
A.4 B.3 C.6 D.5
5.如图,在边长为5的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF.若DF=2,则BE的长为( )
A. B. C. D.2
6.如图,圆柱的底面周长为24厘米,高AB为5厘米,BC是底面直径,一只蚂蚁从点A出发沿着圆柱体的侧面爬行到点C的最短路程是( )
A.6厘米 B.12厘米 C.13厘米 D.16厘米
7.如图,在Rt△ABC中,分别以这个三角形的三边为边长向外侧作正方形、面积分别记为S1,S2,S3.若S3+S2﹣S1=18.则图中阴影部分的面积为( )
A.6 B. C.5 D.
8.如图,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A.1cm B.cm C.cm D.2cm
二、填空题
9.如图所示,正方形的边长为1,则数轴上的点P表示的实数为
10.如图,四边形OABC是长方形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形OABC沿OB折叠,点C落在点D处,则点D的坐标为 .
11.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
12.如图,正方体的棱长为10,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是 .
三、解答题
13.城市绿化是城市重要的基础设施,是改善生态环境和提高广大人民群众生活质量的公益事业.某小区在社区管理人员及社区居民的共同努力之下,在临街清理出了一块可以绿化的空地(图中阴影部分).如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2.
(1)求BC的长;
(2)求图中阴影部分的面积.
14.如图,某人从A地到B地有三条路可选,第一条路从A地沿AB到达B地,AB为10米,第二条路从A地沿折线AC→CB到达B地,AC为8米,BC为6米,第三条路从A地沿折线AD→DB到达B地共行走26米,若C、B、D刚好在一条直线上.
(1)求证:∠C=90°;
(2)求AD的长.
15.如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
16.在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)马里奥在荡绳索过程中离地面的最低点的高度MN.
17.如图,△ABC的三个顶点都在正方形网格的格点上,网格中每个小正方形的边长均为1.
(1)计算:AB= ;BC= ;AC= .
(2)证明:△ABC是直角三角形;
(3)求AC边上的高BD.
18.如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
19.如图,在△ABC中,D是BC的中点,DE⊥BC交AB于点E,且BE2﹣AE2=AC2.
(1)求证:∠A=90°;
(2)若AC=3,BD=2.5,求AE的长.
参考答案
一、选择题
1.【解答】解:选:C.
2.【解答】解:两棵树的高度差为8﹣2=6(米),间距为8米,
根据勾股定理可得:小鸟至少飞行的距离==10(米).
故选:D.
3.【解答】解:选:C.
4.【解答】解:设BN=x,由折叠的性质可得DN=AN=9﹣x,
∵D是BC的中点,BC=6,
∴BD=3,
在Rt△BND中,x2+32=(9﹣x)2,
解得x=4,
即BN=4,
故选:A.
5.【解答】解;如图,把△ADF绕A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴∠ADF=∠ABG=∠ABE=90°,
∴∠ABG+∠ABE=180°,
∴G、B、E三点共线,
∴DF=BG,∠DAF=∠BAG,
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=FE,
设BE=x,
∵CD=5,DF=2,
∴CF=3,
则GE=BG+BE=2+x,CE=5﹣x,
∴EF=2+x,
∵∠C=90°,
∴(5﹣x)2+32=(2+x)2,
解得,x=,
∴BE的长为.
故选:A.
6.【解答】解:如图所示:
由于圆柱体的底面周长为24cm,
则AD=24×=12(cm).
又因为CD=5cm,
所以AC==13(cm).
故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是13cm,
故选:C.
7.【解答】解:在Rt△ABC中,由勾股定理得:AC2+AB2=BC2,
即S1+S2=S3,
∵S3+S2﹣S1=18,
∴S2=9,
由图形可知,阴影部分的面积S2,
∴阴影部分的面积,
故选:B.
8.【解答】解:∵∠C=90°,AC=4cm,BC=3cm,
∴AB===5cm.
根据题意,AE=AB=5,ED=BD.
∴CE=1cm.
设CD=x cm,则ED=(3﹣x)cm.
根据勾股定理得
x2+12=(3﹣x)2,
解得x=.即CD长为cm.
故选:B.
二、填空题
9.【解答】解:如图所示,由图形可知:∠AOB=90°,OA=OB=1,由勾股定理得:,
∴AB=BP=,
∵点B表示的数为2,
∴点P表示的数为:,
故答案为:.
10.【解答】解:由折叠得:∠CBO=∠DBO,
∵矩形ABCO,
∴BC∥OA,
∴∠CBO=∠BOA,
∴∠DBO=∠BOA,
∴BE=OE,
在△ODE和△BAE中,
,
∴△ODE≌△BAE(AAS),
∴AE=DE,
设DE=AE=x,则有OE=BE=8﹣x,
在Rt△ODE中,根据勾股定理得:42+x2=(8﹣x)2,
解得:x=3,即OE=5,DE=3,
过D作DF⊥OA,
∵S△OED=OD DE=OE DF,
∴DF=,OF==,
则D(,﹣).
故答案为:(,﹣)
11.【解答】解:在Rt△ABC中,∠C=90°,
∴AB==4,
以AC为直径的半圆的面积===8π,
以BC为直径的半圆的面积===2π,
以AB为直径的半圆的面积=,
S=16,
∴S阴影=8π+2π+16﹣10π=16,
故答案为:16.
12.【解答】解:如图,将正方体的右侧面与前面展开,构成一个长方形,过B作BC⊥AC于C,
由题意得:AC=10+5=15,BC=10÷2=5,
由勾股定理,得AB===.
故答案为:.
三、解答题
13.【解答】解:(1)在Rt△BCD中,由勾股定理得BC2=BD2+CD2=42+22=20,
∴.
(2)在△ABC中,,
∴△ABC是直角三角形,∠ACB=90°,
∴S阴影=S△ABC﹣S△BCD
=
=
=.
14.【解答】(1)证明:∵AC=8米,BC=6米,AB=10米,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)解:设AD=x米,则BD=(26﹣x)米,
∴CD=BC+BD=6+26﹣x=(32﹣x)(米),
在Rt△ACD中,由勾股定理得:82+( 32﹣x)2=x2,
解得:x=17,
答:AD的长为17米.
15.【解答】解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,
,
∴△ADF≌△AB′E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC﹣FC=18﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18﹣x)2=x2.
解得x=13.
∵△ADF≌△AB′E(已证),
∴AE=AF=13,
∴S△AEF=AE AD=×12×13=78.
16.【解答】解:(1)10﹣3=7(米)
(2)如图:
作AE⊥OM,BF⊥OM,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°
∴∠AOE=∠OBF
在△AOE和△OBF中,,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2×EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m
(3))由勾股定理得OB=OA=ON=13,
∴MN=15﹣13=2(m).
答:马里奥在荡绳索过程中离地面的最低点的高度MN为2米.
17.【解答】解:(1)由勾股定理得,
,,,
(2)∵AB2=13,BC2=52,AC2=65,
∴AB2+BC2=65=AC2
∴△ABC为直角三角形;
(3)作高BD,
由得,
解得,.
18.【解答】解:连接AC,
在Rt△ACD中,
∵AC2=AD2+CD2,
∴AC2=92+122,
解得:AC=15,
在△ABC中,AC=15,AB=20,BC=25,
∵AC2+AB2=BC2,
∴△ABC为直角三角形,
则S四边形ABCD=S△ACD+S△ABC=×9×12+×15×20=204.
即四边形土地ABCD的面积为204.
19.【解答】(1)证明:连接CE,
∵D是BC的中点,DE⊥BC,
∴EB=EC,
∵B E2﹣E A2=A C2,
∴EC2﹣EA2=AC2,
∴EC2=EA2+AC2,
∴∠A=90°.
(2)解:∵D是BC的中点,BD=2.5,
∴BC=2BD=5,
∵∠A=90°,AC=3,
∴,
∵EB=EC,
∴设EB=EC=x,则AE=4﹣x,
在Rt△EAC中
∴32+(4﹣x)2=x2,
解得:
∴.
21世纪教育网(www.21cnjy.com)
第十七章勾股定理期中考试练习人教版2024—2025学年八年级下册
一、选择题
1.下列长度的三条线段能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.6,8,9
2.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行( )米.
A.7 B.8 C.9 D.10
3.下列四组长度的线段中,首尾相连后能构成直角三角形的是( )
A.a=2,b=2, B.a=2,b=3,c=4
C.a=1,, D.a=2,b=2,c=2
4.如图,在Rt△ABC中,AB=9,BC=6,∠ABC=90°.将△ABC折叠,使点A与BC的中点D重合,则BN的长是( )
A.4 B.3 C.6 D.5
5.如图,在边长为5的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF.若DF=2,则BE的长为( )
A. B. C. D.2
6.如图,圆柱的底面周长为24厘米,高AB为5厘米,BC是底面直径,一只蚂蚁从点A出发沿着圆柱体的侧面爬行到点C的最短路程是( )
A.6厘米 B.12厘米 C.13厘米 D.16厘米
7.如图,在Rt△ABC中,分别以这个三角形的三边为边长向外侧作正方形、面积分别记为S1,S2,S3.若S3+S2﹣S1=18.则图中阴影部分的面积为( )
A.6 B. C.5 D.
8.如图,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A.1cm B.cm C.cm D.2cm
二、填空题
9.如图所示,正方形的边长为1,则数轴上的点P表示的实数为
10.如图,四边形OABC是长方形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形OABC沿OB折叠,点C落在点D处,则点D的坐标为 .
11.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
12.如图,正方体的棱长为10,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是 .
三、解答题
13.城市绿化是城市重要的基础设施,是改善生态环境和提高广大人民群众生活质量的公益事业.某小区在社区管理人员及社区居民的共同努力之下,在临街清理出了一块可以绿化的空地(图中阴影部分).如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2.
(1)求BC的长;
(2)求图中阴影部分的面积.
14.如图,某人从A地到B地有三条路可选,第一条路从A地沿AB到达B地,AB为10米,第二条路从A地沿折线AC→CB到达B地,AC为8米,BC为6米,第三条路从A地沿折线AD→DB到达B地共行走26米,若C、B、D刚好在一条直线上.
(1)求证:∠C=90°;
(2)求AD的长.
15.如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
16.在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)马里奥在荡绳索过程中离地面的最低点的高度MN.
17.如图,△ABC的三个顶点都在正方形网格的格点上,网格中每个小正方形的边长均为1.
(1)计算:AB= ;BC= ;AC= .
(2)证明:△ABC是直角三角形;
(3)求AC边上的高BD.
18.如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
19.如图,在△ABC中,D是BC的中点,DE⊥BC交AB于点E,且BE2﹣AE2=AC2.
(1)求证:∠A=90°;
(2)若AC=3,BD=2.5,求AE的长.
参考答案
一、选择题
1.【解答】解:选:C.
2.【解答】解:两棵树的高度差为8﹣2=6(米),间距为8米,
根据勾股定理可得:小鸟至少飞行的距离==10(米).
故选:D.
3.【解答】解:选:C.
4.【解答】解:设BN=x,由折叠的性质可得DN=AN=9﹣x,
∵D是BC的中点,BC=6,
∴BD=3,
在Rt△BND中,x2+32=(9﹣x)2,
解得x=4,
即BN=4,
故选:A.
5.【解答】解;如图,把△ADF绕A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴∠ADF=∠ABG=∠ABE=90°,
∴∠ABG+∠ABE=180°,
∴G、B、E三点共线,
∴DF=BG,∠DAF=∠BAG,
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=FE,
设BE=x,
∵CD=5,DF=2,
∴CF=3,
则GE=BG+BE=2+x,CE=5﹣x,
∴EF=2+x,
∵∠C=90°,
∴(5﹣x)2+32=(2+x)2,
解得,x=,
∴BE的长为.
故选:A.
6.【解答】解:如图所示:
由于圆柱体的底面周长为24cm,
则AD=24×=12(cm).
又因为CD=5cm,
所以AC==13(cm).
故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是13cm,
故选:C.
7.【解答】解:在Rt△ABC中,由勾股定理得:AC2+AB2=BC2,
即S1+S2=S3,
∵S3+S2﹣S1=18,
∴S2=9,
由图形可知,阴影部分的面积S2,
∴阴影部分的面积,
故选:B.
8.【解答】解:∵∠C=90°,AC=4cm,BC=3cm,
∴AB===5cm.
根据题意,AE=AB=5,ED=BD.
∴CE=1cm.
设CD=x cm,则ED=(3﹣x)cm.
根据勾股定理得
x2+12=(3﹣x)2,
解得x=.即CD长为cm.
故选:B.
二、填空题
9.【解答】解:如图所示,由图形可知:∠AOB=90°,OA=OB=1,由勾股定理得:,
∴AB=BP=,
∵点B表示的数为2,
∴点P表示的数为:,
故答案为:.
10.【解答】解:由折叠得:∠CBO=∠DBO,
∵矩形ABCO,
∴BC∥OA,
∴∠CBO=∠BOA,
∴∠DBO=∠BOA,
∴BE=OE,
在△ODE和△BAE中,
,
∴△ODE≌△BAE(AAS),
∴AE=DE,
设DE=AE=x,则有OE=BE=8﹣x,
在Rt△ODE中,根据勾股定理得:42+x2=(8﹣x)2,
解得:x=3,即OE=5,DE=3,
过D作DF⊥OA,
∵S△OED=OD DE=OE DF,
∴DF=,OF==,
则D(,﹣).
故答案为:(,﹣)
11.【解答】解:在Rt△ABC中,∠C=90°,
∴AB==4,
以AC为直径的半圆的面积===8π,
以BC为直径的半圆的面积===2π,
以AB为直径的半圆的面积=,
S=16,
∴S阴影=8π+2π+16﹣10π=16,
故答案为:16.
12.【解答】解:如图,将正方体的右侧面与前面展开,构成一个长方形,过B作BC⊥AC于C,
由题意得:AC=10+5=15,BC=10÷2=5,
由勾股定理,得AB===.
故答案为:.
三、解答题
13.【解答】解:(1)在Rt△BCD中,由勾股定理得BC2=BD2+CD2=42+22=20,
∴.
(2)在△ABC中,,
∴△ABC是直角三角形,∠ACB=90°,
∴S阴影=S△ABC﹣S△BCD
=
=
=.
14.【解答】(1)证明:∵AC=8米,BC=6米,AB=10米,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)解:设AD=x米,则BD=(26﹣x)米,
∴CD=BC+BD=6+26﹣x=(32﹣x)(米),
在Rt△ACD中,由勾股定理得:82+( 32﹣x)2=x2,
解得:x=17,
答:AD的长为17米.
15.【解答】解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,
,
∴△ADF≌△AB′E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC﹣FC=18﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18﹣x)2=x2.
解得x=13.
∵△ADF≌△AB′E(已证),
∴AE=AF=13,
∴S△AEF=AE AD=×12×13=78.
16.【解答】解:(1)10﹣3=7(米)
(2)如图:
作AE⊥OM,BF⊥OM,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°
∴∠AOE=∠OBF
在△AOE和△OBF中,,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2×EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m
(3))由勾股定理得OB=OA=ON=13,
∴MN=15﹣13=2(m).
答:马里奥在荡绳索过程中离地面的最低点的高度MN为2米.
17.【解答】解:(1)由勾股定理得,
,,,
(2)∵AB2=13,BC2=52,AC2=65,
∴AB2+BC2=65=AC2
∴△ABC为直角三角形;
(3)作高BD,
由得,
解得,.
18.【解答】解:连接AC,
在Rt△ACD中,
∵AC2=AD2+CD2,
∴AC2=92+122,
解得:AC=15,
在△ABC中,AC=15,AB=20,BC=25,
∵AC2+AB2=BC2,
∴△ABC为直角三角形,
则S四边形ABCD=S△ACD+S△ABC=×9×12+×15×20=204.
即四边形土地ABCD的面积为204.
19.【解答】(1)证明:连接CE,
∵D是BC的中点,DE⊥BC,
∴EB=EC,
∵B E2﹣E A2=A C2,
∴EC2﹣EA2=AC2,
∴EC2=EA2+AC2,
∴∠A=90°.
(2)解:∵D是BC的中点,BD=2.5,
∴BC=2BD=5,
∵∠A=90°,AC=3,
∴,
∵EB=EC,
∴设EB=EC=x,则AE=4﹣x,
在Rt△EAC中
∴32+(4﹣x)2=x2,
解得:
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
