第七章相交线与平行线章节期中复习人教版2024—2025学年七年级下册
文档属性
| 名称 | 第七章相交线与平行线章节期中复习人教版2024—2025学年七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 511.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 07:45:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章相交线与平行线章节期中复习人教版2024—2025学年七年级下册
一、选择题
1.下列说法错误的是( )
A.在同一平面内,若直线a⊥b,b⊥c,则直线a∥c
B.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
C.相等的两个角一定是对顶角
D.在同一平面内不相交的两条直线是平行线
2.关于如图中各角的说法不正确的是( )
A.∠1与∠2是同旁内角 B.∠1与∠4是内错角
C.∠3与∠5是对顶角 D.∠2与∠3是邻补角
3.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180°
C.∠4=∠5 D.∠1=∠2
4.如图,已知直线l1∥l2,AB⊥CD于点D,∠1=50°,则∠2的度数是( )
A.40° B.45° C.50° D.60°
5.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A.等角的补角相等 B.同角的余角相等
C.等角的余角相等 D.同角的补角相等
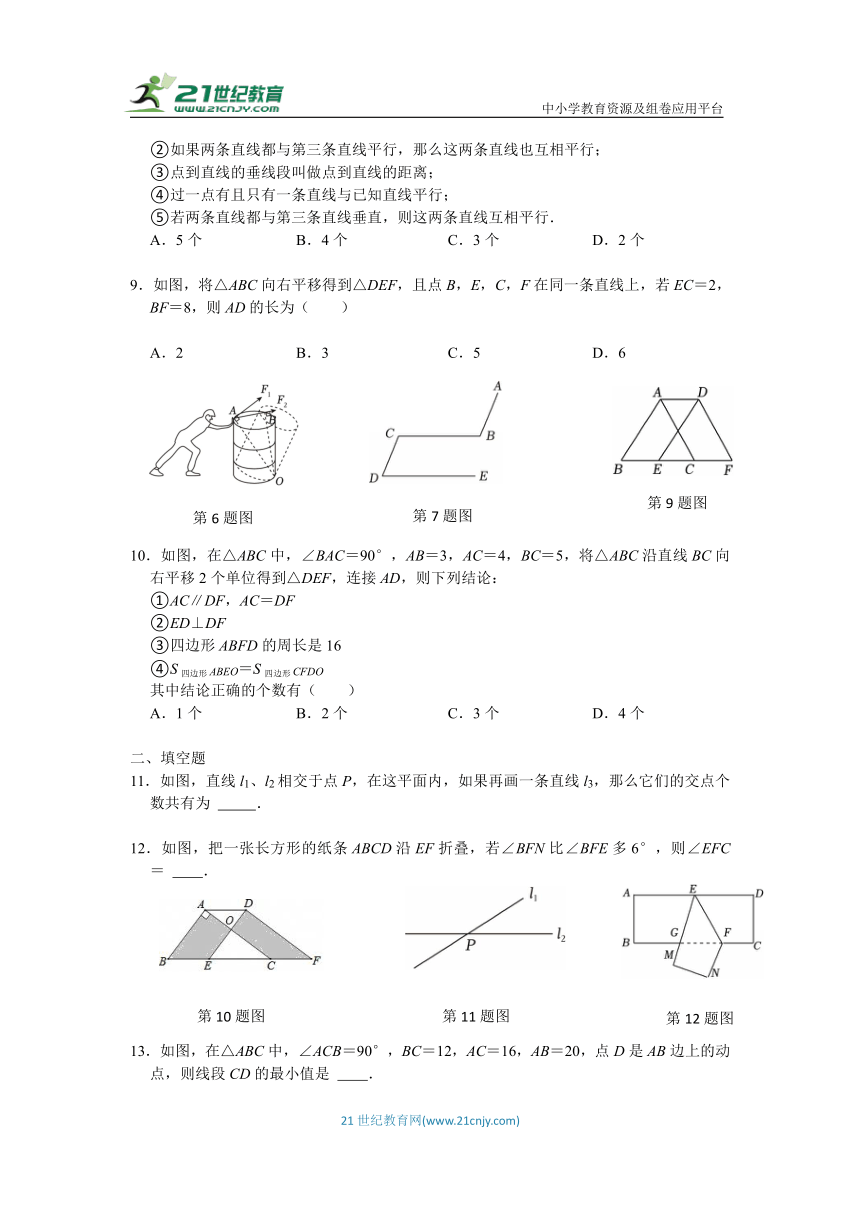
6.如图,推动水桶,以点O为支点,使其向右倾斜.若在点A处分别施加推力F1、F2,则F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是( )
A.垂线段最短
B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线
D.过直线外一点有且只有一条直线与已知直线平行
7.如图,AB∥CD,CB∥DE,若∠B=112°,则∠D的大小为( )
A.68° B.72° C.78° D.82°
8.下列命题中假命题有( )
①两条直线被第三条直线所截,同位角相等;
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
③点到直线的垂线段叫做点到直线的距离;
④过一点有且只有一条直线与已知直线平行;
⑤若两条直线都与第三条直线垂直,则这两条直线互相平行.
A.5个 B.4个 C.3个 D.2个
9.如图,将△ABC向右平移得到△DEF,且点B,E,C,F在同一条直线上,若EC=2,BF=8,则AD的长为( )
A.2 B.3 C.5 D.6
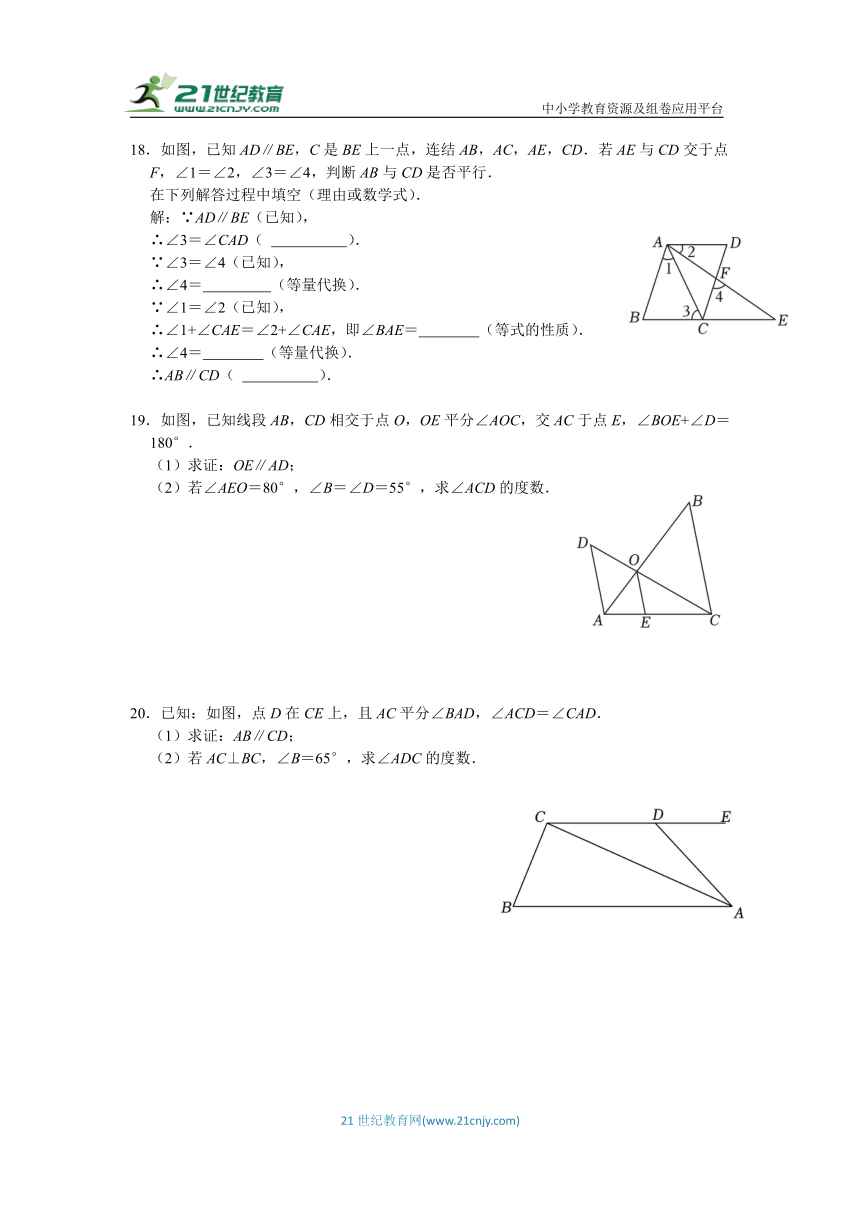
10.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:
①AC∥DF,AC=DF
②ED⊥DF
③四边形ABFD的周长是16
④S四边形ABEO=S四边形CFDO
其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,直线l1、l2相交于点P,在这平面内,如果再画一条直线l3,那么它们的交点个数共有为 .
12.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFN比∠BFE多6°,则∠EFC= .
13.如图,在△ABC中,∠ACB=90°,BC=12,AC=16,AB=20,点D是AB边上的动点,则线段CD的最小值是 .
14.如图,将直角三角形ABC沿BF方向平移得到直角三角形DEF,已知BE=4,AG=3,AC=7,则图中阴影部分的面积为 .
15.如图,直线MN分别交直线AB,CD于点E,F,AB∥CD,EP与FP交于点P,且∠FEP=2∠BEP,∠EFP=3∠DFP,∠BEP=40°,则∠P= .
三、解答题
16.如图,直线AB,CD交于点O,OE⊥AB,垂足为O,∠BOC=130°.
(1)求∠DOE的度数;
(2)若OF平分∠AOD,求∠EOF的度数.
17.如图,已知:点E、O、A在同一直线上,OB平分∠AOC,OD平分∠COE,求证:OD⊥OB.
证明:∵OB平分∠AOC(已知),
∴∠AOC=2∠BOC( ),
同理可得:∠COE=2∠COD,
∵点E、O、A在同一直线上( ),
∴∠AOC+∠COE=180°( ),
∴2∠BOC+2∠COD=180°( ),
∴∠BOC+∠COD=90°( ),
即∠BOD=90°,
∴OD⊥OB( ).
18.如图,已知AD∥BE,C是BE上一点,连结AB,AC,AE,CD.若AE与CD交于点F,∠1=∠2,∠3=∠4,判断AB与CD是否平行.
在下列解答过程中填空(理由或数学式).
解:∵AD∥BE(已知),
∴∠3=∠CAD( ).
∵∠3=∠4(已知),
∴∠4= (等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAE=∠2+∠CAE,即∠BAE= (等式的性质).
∴∠4= (等量代换).
∴AB∥CD( ).
19.如图,已知线段AB,CD相交于点O,OE平分∠AOC,交AC于点E,∠BOE+∠D=180°.
(1)求证:OE∥AD;
(2)若∠AEO=80°,∠B=∠D=55°,求∠ACD的度数.
20.已知:如图,点D在CE上,且AC平分∠BAD,∠ACD=∠CAD.
(1)求证:AB∥CD;
(2)若AC⊥BC,∠B=65°,求∠ADC的度数.
21.如图,点D,E分别在三角形ABC的边AB,AC上,连接DE,CD,点F在CD上,连接EF,其中∠EFC+∠BDC=180°.
(1)求证:∠ADE=∠DEF;
(2)若∠DEF=∠B,∠AED=2∠CDE,求证:∠ACD=∠BCD.
22.如图,AD∥BC,∠BCD的平分线CG交AD于点G.
(1)试说明:∠DGC=∠DCG;
(2)如图,线段CG上有一点P,满足∠CDP=3∠PDG,过点A作AH∥CG交BC于点H.
①若∠BAH=2∠PDG,试判断AB与AD的位置关系,并说明理由;
②在①的条件下,在射线CG上取一点M,使得∠PDM=∠BAH,直线DM交直线BC于点Q,求的值.
参考答案
一、选择题
1.【解答】解:A、在同一平面内,若直线a⊥b,b⊥c,则直线a∥c,故A不符合题意;
B、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故B不符合题意;
C、相等的两个角不一定是对顶角,故C符合题意;
D、在同一平面内不相交的两条直线是平行线,故D不符合题意;
故选:C.
2.【解答】解:A、∠1与∠2是同旁内角,原说法正确,故此选项不符合题意;
B、∠1与∠4不是内错角,原说法错误,故此选项符合题意;
C、∠3与∠5是对顶角,原说法正确,故此选项不符合题意;
D、∠2与∠3是邻补角,原说法正确,故此选项不符合题意.
故选:B.
3.【解答】解:A、当∠1=∠3时,c∥d,故此选项不合题意;
B、当∠2+∠4=180°时,c∥d,故此选项不合题意;
C、当∠4=∠5时,c∥d,故此选项不合题意;
D、当∠1=∠2时,a∥b,故此选项符合题意;
故选:D.
4.【解答】解:∵直线l1∥l2,
∴∠ABC=∠1=50°,
∵AB⊥CD,
∴∠2=90°﹣50°=40°.
故选:A.
5.【解答】解:论证“对顶角相等”使用的依据是:同角的补角相等.
故选:D.
6.【解答】解:F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是垂线段最短.
故选:A.
7.【解答】解:∵AB∥CD,∠B=112°,
∴∠C=∠B=112°,
∵CB∥DE,
∴∠C+∠D=180°,
∴∠D=180°﹣112°=68°.
故选:A.
8.【解答】解:①两条直线被第三条直线所截,同位角相等,错误,缺少平行的条件.
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行,正确.
③点到直线的垂线段叫做点到直线的距离,错误,应该是垂线段的长度.
④过一点有且只有一条直线与已知直线平行,错误,应该是过直线外一点.
⑤若两条直线都与第三条直线垂直,则这两条直线互相平行,错误,条件是同一平面内.
故选:B.
9.【解答】解:∵△DEF是由△ABC向右平移得到,
∴BC=EF,AD=BE,
∴BE=CF=(8﹣2)÷2=3,
∴AD=BE=3.
故选:B.
10.【解答】解:∵将△ABC沿直线BC向右平移2个单位得到△DEF,
∴AC∥DF,AC=DF=4,AB=DE=3,BC=EF=5,AD=BE=CF=2,∠BAC=∠EDF=90°,
∴ED⊥DF.
四边形ABFD的周长=AB+BC+CF+DF+AD=3+5+2+4+2=16.
∵S△ABC=S△DEF,
∴S△ABC﹣S△OEC=S△DEF﹣S△OEC,
∴S四边形ABEO=S四边形CFDO,
即结论正确的有4个.
故选:D.
二、填空题
11.【解答】解:当l3平行于l1或l2时,交点的个数为2个;
当l3与l1和l2都不平行,交于P点时,交点的个数为1个;不交于同一点时,交点的个数为3个.
故答案为:1个或2个或3个.
12.【解答】解:根据折叠的性质得,∠EFC=∠EFN,
∵∠BFN比∠BFE多6°,
∴∠BFN=∠BFE+6°,
∴∠EFC=∠EFN=∠BFN+∠BFE=2∠BFE+6°,
∵∠BFE+∠EFC=180°,
∴2∠BFE+6°+∠BFE=180°,
∴∠BFE=58°,
∴∠EFC=180°﹣58°=122°,
故答案为:122°.
13.【解答】解:由垂线段最短可知,当CD⊥AB时,CD的长度最小,如图.
∵∠ACB=90°,
∴,
∴,
∴CD=9.6.
14.【解答】解:由平移的性质得,S△DEF=S△ACB,DF=AC=7,BE=CF=4,
∴阴影部分的面积=S梯形CFDG,
∵AG=3,AC=7,
∴GC=AC﹣AG=7﹣3=4,
∴,
∴阴影部分的面积为22.
故答案为:22.
15.【解答】解:∵∠FEP=2∠BEP,∠BEP=40°,
∴∠FEP=80°,∠BEF=3∠BEP=120°,
∵AB∥CD,
∴∠EFD+∠BEF=180°,
∴∠EFD=60°,
∵∠EFP=3∠DFP,
∴∠EFP60°=45°,
∴∠P=180°﹣45°﹣80°=55°.
故答案为:55°.
三、解答题
16.【解答】解:(1)∵∠BOC=130°,
∴∠AOD=∠BOC=130°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=130°﹣90°=40°;
(2)∴OF平分∠AOD,
∴∠AOF∠AOD=65°,
∴∠EOF=90°﹣65°=25°.
17.【解答】证明:∵OB平分∠AOC(已知),
∴∠AOC=2∠BOC(平分线的定义),
同理可得:∠COE=2∠COD,
∵点E、O、A在同一直线上(已知),
∴∠AOC+∠COE=180°(平角的定义),
∴2∠BOC+2∠COD=180°(等量代换),
∴∠BOC+∠COD=90°(等式的性质),
即∠BOD=90°,
∴OD⊥OB(垂直的定义).
故答案为:平分线的定义,已知,平角的定义,等量代换,等式的性质,垂直的定义.
18.【解答】解:∵AD∥BE(已知),
∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAE=∠2+∠CAE,即∠BAE=∠CAD(等式的性质).
∴∠4=∠BAE(等量代换).
∴AB∥CD(同位角相等,两直线平行).
故答案为:两直线平行,内错角相等;∠CAD;∠CAD;∠BAE,同位角相等,两直线平行.
19.【解答】(1)证明:∵∠BOE+∠D=180°,∠BOE+∠AOE=180°,
∴∠D=∠AOE,
∵OE平分∠AOC,
∴∠AOE=∠EOC,
∴∠D=∠EOC,
∴AD∥OE;
(2)解:∵∠D=55°,∠D=∠EOC,
∴∠D=∠EOC=55°,
∵∠AEO=80°,
∴∠OEC=180°﹣∠AEO=100°,
∴∠ACD=180°﹣∠OEC﹣∠EOC=25°,
∴∠ACD的度数为25°.
20.【解答】(1)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵∠ACD=∠CAD,
∴∠ACD=∠BAC,
∴AB∥CD;
(2)解:∵AC⊥BC,
∴∠ACB=90°,
∵∠B=65°,
∴∠BAC=90°﹣∠B=90°﹣65°=25°,
∵AC平分∠BAD,
∴∠BAD=2∠BAC=50°,
∵AB∥CD,
∴∠ADC=180°﹣∠BAD=130°,
∴∠ADC的度数为130°.
21.【解答】证明:(1)∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴EF∥AB,
∴∠ADE=∠DEF;
(2)∵∠ADE=∠DEF,∠DEF=∠B,
∴∠ADE=∠B,
∴DE∥BC,
∴∠AED=∠ACB,∠CDE=∠BCD,
又∵∠AED=2∠CDE,
∴∠ACB=2∠BCD,
∴∠ACD=∠ACB﹣∠BCD=2∠BCD﹣∠BCD=∠BCD,
即∠ACD=∠BCD.
22.【解答】解:(1)∵AD∥BC,
∴∠DGC=∠BCG,
∵CG平分∠BCD,
∴∠BCG=∠DCG,
∴∠DGC=∠DCG;
(2)①AB⊥AD,理由如下:
设∠PDG=α,
∵∠CDP=3∠PDG,∠BAH=2∠PDG,
∴∠CDP=3α,∠ADC=4α,∠BAH=2α,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠BCD=180°﹣4α,
∵CG平分∠BCD,
∴∠DCGBCD=90°﹣2α,
由(1)得∠DGC=∠DCG=90°﹣2α,
∵AH∥CG,
∴∠DAH=∠DGC=90°﹣2α,
∵∠BAH=2α,
∴∠BAD=∠DAH+∠BAH=90°﹣2α+2α=90°,
∴AB⊥AD;
②由①得∠DGC=90°﹣2α,
∴∠AGC=180°﹣∠DGC=90°+2α,
过点M作MT∥AD,则∠GMT=∠DGC=90°﹣2α
当点M在线段CG上时,如图,
由①得,∠PDG=α,∠PDM=∠BAH=2α,
∴∠GDM=∠PDG+∠PDM=3α,
∵MT∥AD,
∴∠TMQ=∠GDM=3α,
∴∠GMQ=∠GMT+∠TMQ=90°+α,
∴;
当点M在线段CG的延长线上时,如图,
同理可得,∠GDM=α,
∵MT∥AD,
∴∠TMQ=∠GDM=α,
∴∠GMQ=∠GMT﹣∠TMQ=90°﹣3α,
∴;
综上所述,的值为或.
21世纪教育网(www.21cnjy.com)
第七章相交线与平行线章节期中复习人教版2024—2025学年七年级下册
一、选择题
1.下列说法错误的是( )
A.在同一平面内,若直线a⊥b,b⊥c,则直线a∥c
B.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
C.相等的两个角一定是对顶角
D.在同一平面内不相交的两条直线是平行线
2.关于如图中各角的说法不正确的是( )
A.∠1与∠2是同旁内角 B.∠1与∠4是内错角
C.∠3与∠5是对顶角 D.∠2与∠3是邻补角
3.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180°
C.∠4=∠5 D.∠1=∠2
4.如图,已知直线l1∥l2,AB⊥CD于点D,∠1=50°,则∠2的度数是( )
A.40° B.45° C.50° D.60°
5.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A.等角的补角相等 B.同角的余角相等
C.等角的余角相等 D.同角的补角相等
6.如图,推动水桶,以点O为支点,使其向右倾斜.若在点A处分别施加推力F1、F2,则F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是( )
A.垂线段最短
B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线
D.过直线外一点有且只有一条直线与已知直线平行
7.如图,AB∥CD,CB∥DE,若∠B=112°,则∠D的大小为( )
A.68° B.72° C.78° D.82°
8.下列命题中假命题有( )
①两条直线被第三条直线所截,同位角相等;
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
③点到直线的垂线段叫做点到直线的距离;
④过一点有且只有一条直线与已知直线平行;
⑤若两条直线都与第三条直线垂直,则这两条直线互相平行.
A.5个 B.4个 C.3个 D.2个
9.如图,将△ABC向右平移得到△DEF,且点B,E,C,F在同一条直线上,若EC=2,BF=8,则AD的长为( )
A.2 B.3 C.5 D.6
10.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:
①AC∥DF,AC=DF
②ED⊥DF
③四边形ABFD的周长是16
④S四边形ABEO=S四边形CFDO
其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,直线l1、l2相交于点P,在这平面内,如果再画一条直线l3,那么它们的交点个数共有为 .
12.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFN比∠BFE多6°,则∠EFC= .
13.如图,在△ABC中,∠ACB=90°,BC=12,AC=16,AB=20,点D是AB边上的动点,则线段CD的最小值是 .
14.如图,将直角三角形ABC沿BF方向平移得到直角三角形DEF,已知BE=4,AG=3,AC=7,则图中阴影部分的面积为 .
15.如图,直线MN分别交直线AB,CD于点E,F,AB∥CD,EP与FP交于点P,且∠FEP=2∠BEP,∠EFP=3∠DFP,∠BEP=40°,则∠P= .
三、解答题
16.如图,直线AB,CD交于点O,OE⊥AB,垂足为O,∠BOC=130°.
(1)求∠DOE的度数;
(2)若OF平分∠AOD,求∠EOF的度数.
17.如图,已知:点E、O、A在同一直线上,OB平分∠AOC,OD平分∠COE,求证:OD⊥OB.
证明:∵OB平分∠AOC(已知),
∴∠AOC=2∠BOC( ),
同理可得:∠COE=2∠COD,
∵点E、O、A在同一直线上( ),
∴∠AOC+∠COE=180°( ),
∴2∠BOC+2∠COD=180°( ),
∴∠BOC+∠COD=90°( ),
即∠BOD=90°,
∴OD⊥OB( ).
18.如图,已知AD∥BE,C是BE上一点,连结AB,AC,AE,CD.若AE与CD交于点F,∠1=∠2,∠3=∠4,判断AB与CD是否平行.
在下列解答过程中填空(理由或数学式).
解:∵AD∥BE(已知),
∴∠3=∠CAD( ).
∵∠3=∠4(已知),
∴∠4= (等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAE=∠2+∠CAE,即∠BAE= (等式的性质).
∴∠4= (等量代换).
∴AB∥CD( ).
19.如图,已知线段AB,CD相交于点O,OE平分∠AOC,交AC于点E,∠BOE+∠D=180°.
(1)求证:OE∥AD;
(2)若∠AEO=80°,∠B=∠D=55°,求∠ACD的度数.
20.已知:如图,点D在CE上,且AC平分∠BAD,∠ACD=∠CAD.
(1)求证:AB∥CD;
(2)若AC⊥BC,∠B=65°,求∠ADC的度数.
21.如图,点D,E分别在三角形ABC的边AB,AC上,连接DE,CD,点F在CD上,连接EF,其中∠EFC+∠BDC=180°.
(1)求证:∠ADE=∠DEF;
(2)若∠DEF=∠B,∠AED=2∠CDE,求证:∠ACD=∠BCD.
22.如图,AD∥BC,∠BCD的平分线CG交AD于点G.
(1)试说明:∠DGC=∠DCG;
(2)如图,线段CG上有一点P,满足∠CDP=3∠PDG,过点A作AH∥CG交BC于点H.
①若∠BAH=2∠PDG,试判断AB与AD的位置关系,并说明理由;
②在①的条件下,在射线CG上取一点M,使得∠PDM=∠BAH,直线DM交直线BC于点Q,求的值.
参考答案
一、选择题
1.【解答】解:A、在同一平面内,若直线a⊥b,b⊥c,则直线a∥c,故A不符合题意;
B、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故B不符合题意;
C、相等的两个角不一定是对顶角,故C符合题意;
D、在同一平面内不相交的两条直线是平行线,故D不符合题意;
故选:C.
2.【解答】解:A、∠1与∠2是同旁内角,原说法正确,故此选项不符合题意;
B、∠1与∠4不是内错角,原说法错误,故此选项符合题意;
C、∠3与∠5是对顶角,原说法正确,故此选项不符合题意;
D、∠2与∠3是邻补角,原说法正确,故此选项不符合题意.
故选:B.
3.【解答】解:A、当∠1=∠3时,c∥d,故此选项不合题意;
B、当∠2+∠4=180°时,c∥d,故此选项不合题意;
C、当∠4=∠5时,c∥d,故此选项不合题意;
D、当∠1=∠2时,a∥b,故此选项符合题意;
故选:D.
4.【解答】解:∵直线l1∥l2,
∴∠ABC=∠1=50°,
∵AB⊥CD,
∴∠2=90°﹣50°=40°.
故选:A.
5.【解答】解:论证“对顶角相等”使用的依据是:同角的补角相等.
故选:D.
6.【解答】解:F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是垂线段最短.
故选:A.
7.【解答】解:∵AB∥CD,∠B=112°,
∴∠C=∠B=112°,
∵CB∥DE,
∴∠C+∠D=180°,
∴∠D=180°﹣112°=68°.
故选:A.
8.【解答】解:①两条直线被第三条直线所截,同位角相等,错误,缺少平行的条件.
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行,正确.
③点到直线的垂线段叫做点到直线的距离,错误,应该是垂线段的长度.
④过一点有且只有一条直线与已知直线平行,错误,应该是过直线外一点.
⑤若两条直线都与第三条直线垂直,则这两条直线互相平行,错误,条件是同一平面内.
故选:B.
9.【解答】解:∵△DEF是由△ABC向右平移得到,
∴BC=EF,AD=BE,
∴BE=CF=(8﹣2)÷2=3,
∴AD=BE=3.
故选:B.
10.【解答】解:∵将△ABC沿直线BC向右平移2个单位得到△DEF,
∴AC∥DF,AC=DF=4,AB=DE=3,BC=EF=5,AD=BE=CF=2,∠BAC=∠EDF=90°,
∴ED⊥DF.
四边形ABFD的周长=AB+BC+CF+DF+AD=3+5+2+4+2=16.
∵S△ABC=S△DEF,
∴S△ABC﹣S△OEC=S△DEF﹣S△OEC,
∴S四边形ABEO=S四边形CFDO,
即结论正确的有4个.
故选:D.
二、填空题
11.【解答】解:当l3平行于l1或l2时,交点的个数为2个;
当l3与l1和l2都不平行,交于P点时,交点的个数为1个;不交于同一点时,交点的个数为3个.
故答案为:1个或2个或3个.
12.【解答】解:根据折叠的性质得,∠EFC=∠EFN,
∵∠BFN比∠BFE多6°,
∴∠BFN=∠BFE+6°,
∴∠EFC=∠EFN=∠BFN+∠BFE=2∠BFE+6°,
∵∠BFE+∠EFC=180°,
∴2∠BFE+6°+∠BFE=180°,
∴∠BFE=58°,
∴∠EFC=180°﹣58°=122°,
故答案为:122°.
13.【解答】解:由垂线段最短可知,当CD⊥AB时,CD的长度最小,如图.
∵∠ACB=90°,
∴,
∴,
∴CD=9.6.
14.【解答】解:由平移的性质得,S△DEF=S△ACB,DF=AC=7,BE=CF=4,
∴阴影部分的面积=S梯形CFDG,
∵AG=3,AC=7,
∴GC=AC﹣AG=7﹣3=4,
∴,
∴阴影部分的面积为22.
故答案为:22.
15.【解答】解:∵∠FEP=2∠BEP,∠BEP=40°,
∴∠FEP=80°,∠BEF=3∠BEP=120°,
∵AB∥CD,
∴∠EFD+∠BEF=180°,
∴∠EFD=60°,
∵∠EFP=3∠DFP,
∴∠EFP60°=45°,
∴∠P=180°﹣45°﹣80°=55°.
故答案为:55°.
三、解答题
16.【解答】解:(1)∵∠BOC=130°,
∴∠AOD=∠BOC=130°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=130°﹣90°=40°;
(2)∴OF平分∠AOD,
∴∠AOF∠AOD=65°,
∴∠EOF=90°﹣65°=25°.
17.【解答】证明:∵OB平分∠AOC(已知),
∴∠AOC=2∠BOC(平分线的定义),
同理可得:∠COE=2∠COD,
∵点E、O、A在同一直线上(已知),
∴∠AOC+∠COE=180°(平角的定义),
∴2∠BOC+2∠COD=180°(等量代换),
∴∠BOC+∠COD=90°(等式的性质),
即∠BOD=90°,
∴OD⊥OB(垂直的定义).
故答案为:平分线的定义,已知,平角的定义,等量代换,等式的性质,垂直的定义.
18.【解答】解:∵AD∥BE(已知),
∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAE=∠2+∠CAE,即∠BAE=∠CAD(等式的性质).
∴∠4=∠BAE(等量代换).
∴AB∥CD(同位角相等,两直线平行).
故答案为:两直线平行,内错角相等;∠CAD;∠CAD;∠BAE,同位角相等,两直线平行.
19.【解答】(1)证明:∵∠BOE+∠D=180°,∠BOE+∠AOE=180°,
∴∠D=∠AOE,
∵OE平分∠AOC,
∴∠AOE=∠EOC,
∴∠D=∠EOC,
∴AD∥OE;
(2)解:∵∠D=55°,∠D=∠EOC,
∴∠D=∠EOC=55°,
∵∠AEO=80°,
∴∠OEC=180°﹣∠AEO=100°,
∴∠ACD=180°﹣∠OEC﹣∠EOC=25°,
∴∠ACD的度数为25°.
20.【解答】(1)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵∠ACD=∠CAD,
∴∠ACD=∠BAC,
∴AB∥CD;
(2)解:∵AC⊥BC,
∴∠ACB=90°,
∵∠B=65°,
∴∠BAC=90°﹣∠B=90°﹣65°=25°,
∵AC平分∠BAD,
∴∠BAD=2∠BAC=50°,
∵AB∥CD,
∴∠ADC=180°﹣∠BAD=130°,
∴∠ADC的度数为130°.
21.【解答】证明:(1)∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴EF∥AB,
∴∠ADE=∠DEF;
(2)∵∠ADE=∠DEF,∠DEF=∠B,
∴∠ADE=∠B,
∴DE∥BC,
∴∠AED=∠ACB,∠CDE=∠BCD,
又∵∠AED=2∠CDE,
∴∠ACB=2∠BCD,
∴∠ACD=∠ACB﹣∠BCD=2∠BCD﹣∠BCD=∠BCD,
即∠ACD=∠BCD.
22.【解答】解:(1)∵AD∥BC,
∴∠DGC=∠BCG,
∵CG平分∠BCD,
∴∠BCG=∠DCG,
∴∠DGC=∠DCG;
(2)①AB⊥AD,理由如下:
设∠PDG=α,
∵∠CDP=3∠PDG,∠BAH=2∠PDG,
∴∠CDP=3α,∠ADC=4α,∠BAH=2α,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠BCD=180°﹣4α,
∵CG平分∠BCD,
∴∠DCGBCD=90°﹣2α,
由(1)得∠DGC=∠DCG=90°﹣2α,
∵AH∥CG,
∴∠DAH=∠DGC=90°﹣2α,
∵∠BAH=2α,
∴∠BAD=∠DAH+∠BAH=90°﹣2α+2α=90°,
∴AB⊥AD;
②由①得∠DGC=90°﹣2α,
∴∠AGC=180°﹣∠DGC=90°+2α,
过点M作MT∥AD,则∠GMT=∠DGC=90°﹣2α
当点M在线段CG上时,如图,
由①得,∠PDG=α,∠PDM=∠BAH=2α,
∴∠GDM=∠PDG+∠PDM=3α,
∵MT∥AD,
∴∠TMQ=∠GDM=3α,
∴∠GMQ=∠GMT+∠TMQ=90°+α,
∴;
当点M在线段CG的延长线上时,如图,
同理可得,∠GDM=α,
∵MT∥AD,
∴∠TMQ=∠GDM=α,
∴∠GMQ=∠GMT﹣∠TMQ=90°﹣3α,
∴;
综上所述,的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
