2025年九年级数学中考三轮冲刺练习(二)(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 14:50:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺练习(二)
一、选择题
1.已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )
A.x1≠x2 B.x1+x2>0 C.x1 x2>0 D.x1<0,x2<0
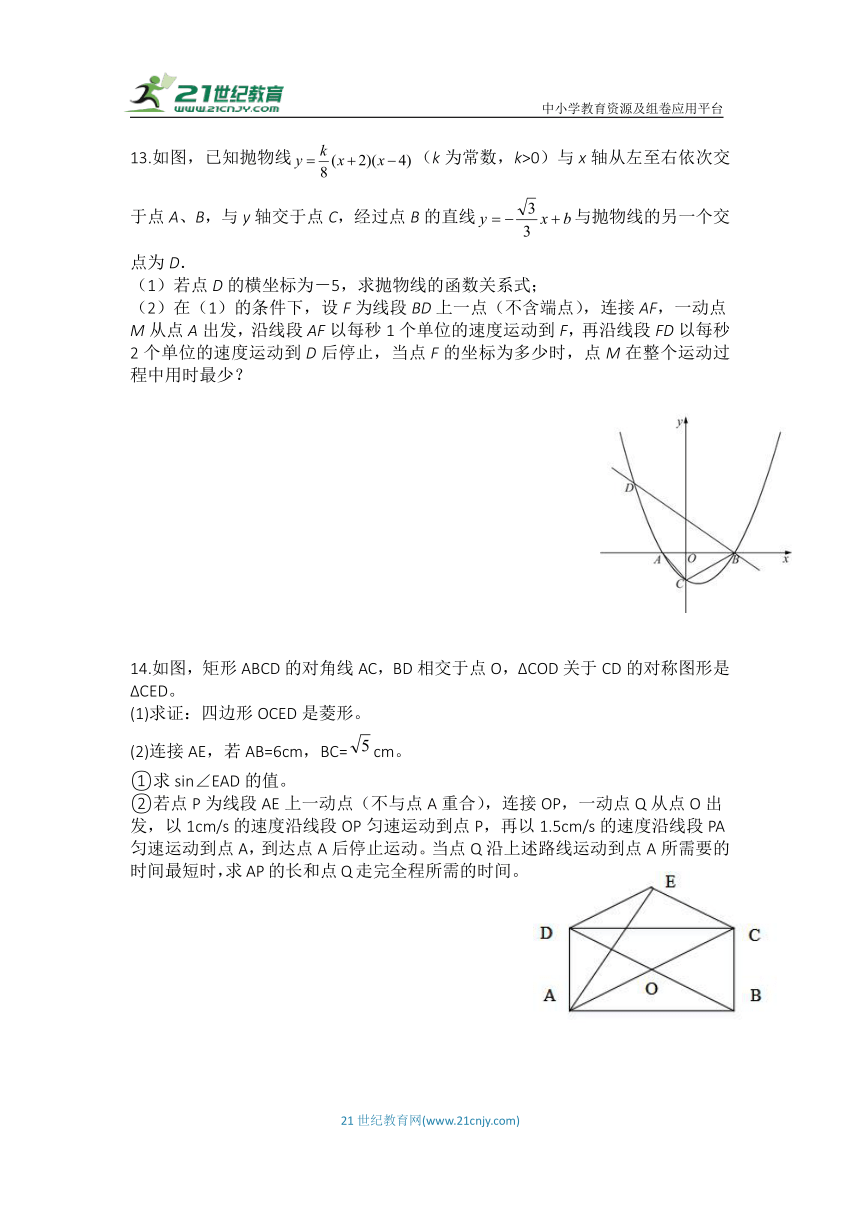
2.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG=( )
A. B.3 C. D.
3.如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣3,6),B(6,3),直线y=kx﹣3与线段AB有交点,则k的值不可能是( )
A.﹣2 B.﹣4 C.2 D.4
4.如图,矩形ABCD内接于⊙O,点P是上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为( )
A. B. C. D.
5.如图,在平面直角坐标系xOy中,A(﹣3,0),B(3,0),若在直线y=﹣x+m上存在点P满足∠APB=60°,则m的取值范围是( )
A.≤m≤ B.﹣﹣5≤m≤+5
C.﹣2≤m≤+2 D.﹣﹣2≤m≤+2
二、填空题
6.若三角形的三条边长分别为5,12,13,则这个三角形外接圆的半径为 .
7.若二次函数y=2(x+1)2+3的图象上有三个不同的点A(x1,m)、B(x1+x2,n)、C(x2,m),则n的值为 .
8.已知函数y=,若使y=k成立的x值恰好有2个,则k的值为 .
三、解答题
9.已知实数a满足a2+2a﹣15=0,求﹣÷的值.
103月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向M、N两地之间修建一条道路.已知:如图C点周围180m范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上.
(1)NM是否穿过文物保护区?为什么?(参考数据:≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工作需要多少天?
11.如图1,在⊙O中,AB为直径,BC为切线,弦BE⊥OC,连CE.
(1)求证:CE为⊙O的切线;
(2)如图2,CF⊥BC交AE的延长线于F,BC=AB,求的值.
12.已知抛物线G:y=x2+(k﹣5)x+1﹣k,其中k为常数.
(1)若抛物线G的图象不经过第三象限,求k的取值范围;
(2)对于一个函数,当自变量x取a时,函数值y也等于a,我们称a为这个函数的对等值.若函数y=x2+(k﹣5)x+1﹣k有两相异的对等值x1,x2,且x1<2<x2,求k的最大整数值.
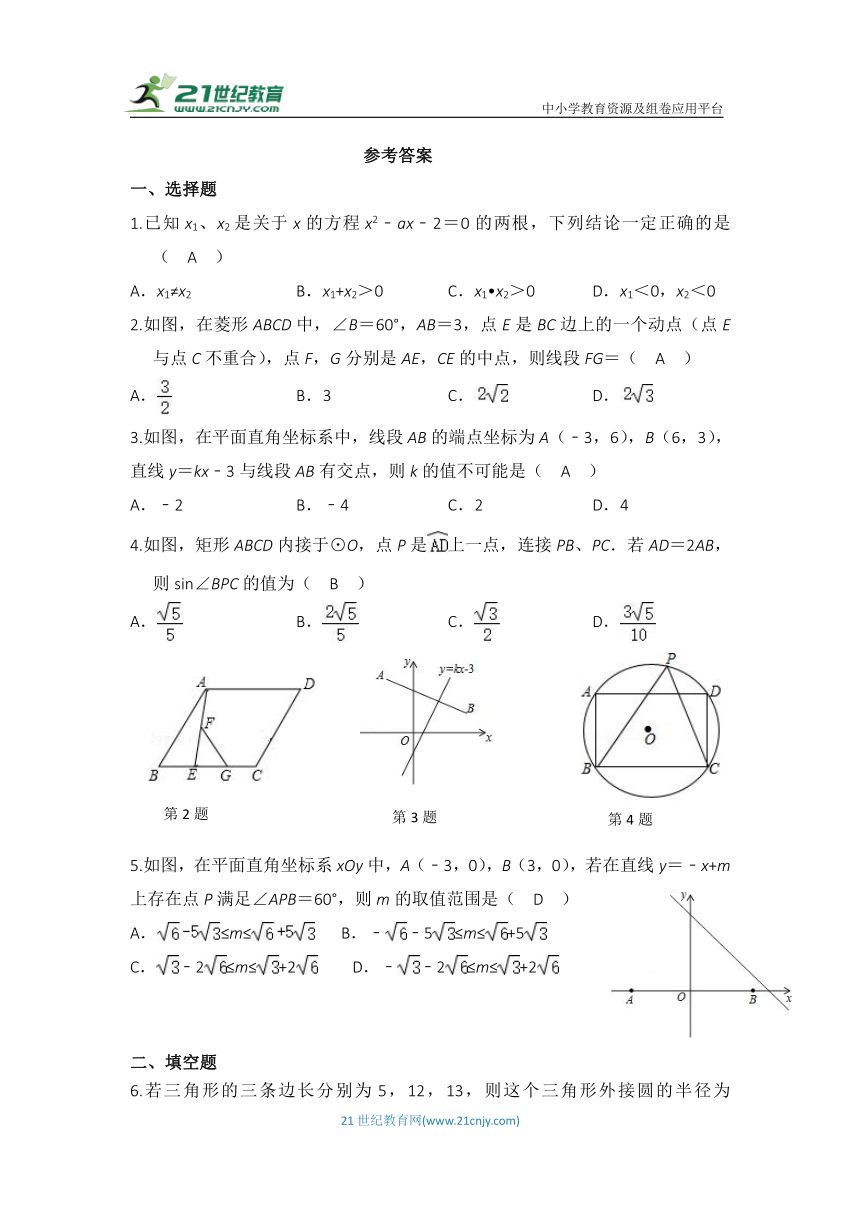
13.如图,已知抛物线(k为常数,k>0)与x轴从左至右依次交于点A、B,与y轴交于点C,经过点B的直线与抛物线的另一个交点为D.
(1)若点D的横坐标为-5,求抛物线的函数关系式;
(2)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标为多少时,点M在整个运动过程中用时最少?
14.如图,矩形ABCD的对角线AC,BD相交于点O,ΔCOD关于CD的对称图形是ΔCED。
(1)求证:四边形OCED是菱形。
(2)连接AE,若AB=6cm,BC=cm。
①求sin∠EAD的值。
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动。当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间。
参考答案
一、选择题
1.已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( A )
A.x1≠x2 B.x1+x2>0 C.x1 x2>0 D.x1<0,x2<0
2.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG=( A )
A. B.3 C. D.
3.如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣3,6),B(6,3),直线y=kx﹣3与线段AB有交点,则k的值不可能是( A )
A.﹣2 B.﹣4 C.2 D.4
4.如图,矩形ABCD内接于⊙O,点P是上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为( B )
A. B. C. D.
5.如图,在平面直角坐标系xOy中,A(﹣3,0),B(3,0),若在直线y=﹣x+m上存在点P满足∠APB=60°,则m的取值范围是( D )
A.≤m≤ B.﹣﹣5≤m≤+5
C.﹣2≤m≤+2 D.﹣﹣2≤m≤+2
二、填空题
6.若三角形的三条边长分别为5,12,13,则这个三角形外接圆的半径为 6.5 .
7.若二次函数y=2(x+1)2+3的图象上有三个不同的点A(x1,m)、B(x1+x2,n)、C(x2,m),则n的值为 5 .
8.已知函数y=,若使y=k成立的x值恰好有2个,则k的值为
k=﹣1或k>3 .
三、解答题
9.已知实数a满足a2+2a﹣15=0,求﹣÷的值.
解:﹣÷=﹣ =﹣=,
∵a2+2a﹣15=0,
∴(a+1)2=16,
∴原式==.
10.3月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向M、N两地之间修建一条道路.已知:如图C点周围180m范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上.
(1)NM是否穿过文物保护区?为什么?(参考数据:≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工作需要多少天?
解:(1)由示意图可得:∠A=30°,∠B=45°,AB=500m,
设C到AB的距离为h,则可得:
tan30°=,
∴AD=h,
h+h=500,
解得:h=250(﹣1)≈183m,
∵h>180m,
∴NM不穿过文物保护区.
(2)设原计划完成这项工作需要x天,则
×(1+25%)=,解得:x=25
经检验,x=25是原方程的解.
答:原计划完成这项工作需要25天.
11.如图1,在⊙O中,AB为直径,BC为切线,弦BE⊥OC,连CE.
(1)求证:CE为⊙O的切线;
(2)如图2,CF⊥BC交AE的延长线于F,BC=AB,求的值.
(1)证明:连接OE,如图1所示:
则OB=OE,设OC与BE交于点H,
∵OC⊥BE,∴H为BE的中点,∴OC垂直平分BE,
∴BC=EC,在△OEC和△OBC中,,∴△OEC≌△OBC(SSS),
∴∠OEC=∠OBC,∵BC为切线,AB为直径,
∴∠OBC=90°,∴∠OEC=90°,
∴CE为⊙O的切线;
(2)解:∵AB为直径,
∴∠AEB=90°=∠OHB,
∴OC∥AF,
∵AB⊥BC,CF⊥BC,
∴AB∥CF,
∴四边形AOCF为平行四边形,
∴AF=OC,
∵BE⊥OC,
∴BH=HE,
∴OH是△BAE的中位线,
设OH=x,则AE=2OH=2x,
∠AEB=∠BHC=90°,
∠BCH=∠ABE=90°﹣∠CBH,
在△ABE和△BCH中,,
∴△ABE≌△BCH(AAS),
∴BH=AE=2x,
∴OB===x,
∴BC=AB=2OB=2x,
∴OC===5x,
∴AF=OC=5x,
EF=AF﹣AE=5x﹣2x=3x,
∴==.
12.已知抛物线G:y=x2+(k﹣5)x+1﹣k,其中k为常数.
(1)若抛物线G的图象不经过第三象限,求k的取值范围;
(2)对于一个函数,当自变量x取a时,函数值y也等于a,我们称a为这个函数的对等值.若函数y=x2+(k﹣5)x+1﹣k有两相异的对等值x1,x2,且x1<2<x2,求k的最大整数值.
解:(1)∵y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,
又a=1>0,△=(k﹣5)2﹣4(1﹣k)=(k﹣3)2+12,
∴抛物线与x轴有两个交点,
设抛物线与x轴交点的横坐标分别为x1,x2,
∴x1+x2=5﹣k>0,x1x2=1﹣k≥0,
解得k≤1,
∴k的取值范围为k≤1;
(2)依题意,得:x2+(k﹣5)x+1﹣k=x,
∴x2+(k﹣6)x+1﹣k=0,
∵△=(k﹣4)2+16>0,
∴k为任意实数,
又x1+x2=6﹣k,x1x2=1﹣k,
∵(x1﹣2)(x2﹣2)<0,
∴x1x2﹣2(x1+x2)+4<0,
∴1﹣k﹣2(6﹣k)+4<0,
∴k<7,
∴综上,k的最大整数值为6.
13.如图,已知抛物线(k为常数,k>0)与x轴从左至右依次交于点A、B,与y轴交于点C,经过点B的直线与抛物线的另一个交点为D.
(1)若点D的横坐标为-5,求抛物线的函数关系式;
(2)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标为多少时,点M在整个运动过程中用时最少?
解:(1)抛物线y=x2﹣x﹣k,
令y=0,解得x=﹣2或x=4,
∴A(﹣2,0),B(4,0).
∵直线y=﹣x+b经过点B(4,0),
∴﹣×4+b=0,解得b=,
∴直线BD解析式为:y=﹣x+.
当x=﹣5时,y=3,
∴D(﹣5,3).
∵点D(﹣5,3)在抛物线y=(x+2)(x﹣4)上,
∴(﹣5+2)(﹣5﹣4)=3,
∴k=.
∴抛物线的函数表达式为:y=(x+2)(x﹣4).
即y=x2﹣x﹣;
(2)如答图3,由(1)知:D(﹣5,3),
如答图2﹣2,过点D作DN⊥x轴于点N,则DN=3,ON=5,BN=4+5=9,
∴tan∠DBA===,
∴∠DBA=30°.
过点D作DK∥x轴,则∠KDF=∠DBA=30°.
过点F作FG⊥DK于点G,则FG=DF.
由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+DF,
∴t=AF+FG,即运动的时间值等于折线AF+FG的长度值.
由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.
过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求之F点.
∵A点横坐标为﹣2,直线BD解析式为:y=﹣x+,
∴y=﹣×(﹣2)+=2,
∴F(﹣2,2).
综上所述,当点F坐标为(﹣2,2)时,点M在整个运动过程中用时最少.
14.如图,矩形ABCD的对角线AC,BD相交于点O,ΔCOD关于CD的对称图形是ΔCED。
(1)求证:四边形OCED是菱形。
(2)连接AE,若AB=6cm,BC=cm。
①求sin∠EAD的值。
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动。当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间。
(1)证明:∵四边形ABCD是矩形.
∴OD=OB=OC=OA,
∵△EDC和△ODC关于CD对称,
∴DE=DO,CE=CO,
∴DE=EC=CO=OD,
∴四边形CODE是菱形.
(2)①设AE交CD于K.
∵四边形CODE是菱形,
∴DE∥AC,DE=OC=OA,
∴==
∵AB=CD=6,
∴DK=2,CK=4,
在Rt△ADK中,AK===3,
∴sin∠DAE==,
②作PF⊥AD于F.易知PF=AP sin∠DAE=AP,
∵点Q的运动时间t=+=OP+AP=OP+PF,
∴当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,
∴OF=CD=3.AF=AD=,PF=DK=1,
∴AP==,
∴当点Q沿上述路线运动到点A所需要的时间最短时,AP的长为cm,点Q走完全程所需的时间为3s.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺练习(二)
一、选择题
1.已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )
A.x1≠x2 B.x1+x2>0 C.x1 x2>0 D.x1<0,x2<0
2.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG=( )
A. B.3 C. D.
3.如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣3,6),B(6,3),直线y=kx﹣3与线段AB有交点,则k的值不可能是( )
A.﹣2 B.﹣4 C.2 D.4
4.如图,矩形ABCD内接于⊙O,点P是上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为( )
A. B. C. D.
5.如图,在平面直角坐标系xOy中,A(﹣3,0),B(3,0),若在直线y=﹣x+m上存在点P满足∠APB=60°,则m的取值范围是( )
A.≤m≤ B.﹣﹣5≤m≤+5
C.﹣2≤m≤+2 D.﹣﹣2≤m≤+2
二、填空题
6.若三角形的三条边长分别为5,12,13,则这个三角形外接圆的半径为 .
7.若二次函数y=2(x+1)2+3的图象上有三个不同的点A(x1,m)、B(x1+x2,n)、C(x2,m),则n的值为 .
8.已知函数y=,若使y=k成立的x值恰好有2个,则k的值为 .
三、解答题
9.已知实数a满足a2+2a﹣15=0,求﹣÷的值.
103月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向M、N两地之间修建一条道路.已知:如图C点周围180m范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上.
(1)NM是否穿过文物保护区?为什么?(参考数据:≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工作需要多少天?
11.如图1,在⊙O中,AB为直径,BC为切线,弦BE⊥OC,连CE.
(1)求证:CE为⊙O的切线;
(2)如图2,CF⊥BC交AE的延长线于F,BC=AB,求的值.
12.已知抛物线G:y=x2+(k﹣5)x+1﹣k,其中k为常数.
(1)若抛物线G的图象不经过第三象限,求k的取值范围;
(2)对于一个函数,当自变量x取a时,函数值y也等于a,我们称a为这个函数的对等值.若函数y=x2+(k﹣5)x+1﹣k有两相异的对等值x1,x2,且x1<2<x2,求k的最大整数值.
13.如图,已知抛物线(k为常数,k>0)与x轴从左至右依次交于点A、B,与y轴交于点C,经过点B的直线与抛物线的另一个交点为D.
(1)若点D的横坐标为-5,求抛物线的函数关系式;
(2)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标为多少时,点M在整个运动过程中用时最少?
14.如图,矩形ABCD的对角线AC,BD相交于点O,ΔCOD关于CD的对称图形是ΔCED。
(1)求证:四边形OCED是菱形。
(2)连接AE,若AB=6cm,BC=cm。
①求sin∠EAD的值。
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动。当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间。
参考答案
一、选择题
1.已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( A )
A.x1≠x2 B.x1+x2>0 C.x1 x2>0 D.x1<0,x2<0
2.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG=( A )
A. B.3 C. D.
3.如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣3,6),B(6,3),直线y=kx﹣3与线段AB有交点,则k的值不可能是( A )
A.﹣2 B.﹣4 C.2 D.4
4.如图,矩形ABCD内接于⊙O,点P是上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为( B )
A. B. C. D.
5.如图,在平面直角坐标系xOy中,A(﹣3,0),B(3,0),若在直线y=﹣x+m上存在点P满足∠APB=60°,则m的取值范围是( D )
A.≤m≤ B.﹣﹣5≤m≤+5
C.﹣2≤m≤+2 D.﹣﹣2≤m≤+2
二、填空题
6.若三角形的三条边长分别为5,12,13,则这个三角形外接圆的半径为 6.5 .
7.若二次函数y=2(x+1)2+3的图象上有三个不同的点A(x1,m)、B(x1+x2,n)、C(x2,m),则n的值为 5 .
8.已知函数y=,若使y=k成立的x值恰好有2个,则k的值为
k=﹣1或k>3 .
三、解答题
9.已知实数a满足a2+2a﹣15=0,求﹣÷的值.
解:﹣÷=﹣ =﹣=,
∵a2+2a﹣15=0,
∴(a+1)2=16,
∴原式==.
10.3月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向M、N两地之间修建一条道路.已知:如图C点周围180m范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上.
(1)NM是否穿过文物保护区?为什么?(参考数据:≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工作需要多少天?
解:(1)由示意图可得:∠A=30°,∠B=45°,AB=500m,
设C到AB的距离为h,则可得:
tan30°=,
∴AD=h,
h+h=500,
解得:h=250(﹣1)≈183m,
∵h>180m,
∴NM不穿过文物保护区.
(2)设原计划完成这项工作需要x天,则
×(1+25%)=,解得:x=25
经检验,x=25是原方程的解.
答:原计划完成这项工作需要25天.
11.如图1,在⊙O中,AB为直径,BC为切线,弦BE⊥OC,连CE.
(1)求证:CE为⊙O的切线;
(2)如图2,CF⊥BC交AE的延长线于F,BC=AB,求的值.
(1)证明:连接OE,如图1所示:
则OB=OE,设OC与BE交于点H,
∵OC⊥BE,∴H为BE的中点,∴OC垂直平分BE,
∴BC=EC,在△OEC和△OBC中,,∴△OEC≌△OBC(SSS),
∴∠OEC=∠OBC,∵BC为切线,AB为直径,
∴∠OBC=90°,∴∠OEC=90°,
∴CE为⊙O的切线;
(2)解:∵AB为直径,
∴∠AEB=90°=∠OHB,
∴OC∥AF,
∵AB⊥BC,CF⊥BC,
∴AB∥CF,
∴四边形AOCF为平行四边形,
∴AF=OC,
∵BE⊥OC,
∴BH=HE,
∴OH是△BAE的中位线,
设OH=x,则AE=2OH=2x,
∠AEB=∠BHC=90°,
∠BCH=∠ABE=90°﹣∠CBH,
在△ABE和△BCH中,,
∴△ABE≌△BCH(AAS),
∴BH=AE=2x,
∴OB===x,
∴BC=AB=2OB=2x,
∴OC===5x,
∴AF=OC=5x,
EF=AF﹣AE=5x﹣2x=3x,
∴==.
12.已知抛物线G:y=x2+(k﹣5)x+1﹣k,其中k为常数.
(1)若抛物线G的图象不经过第三象限,求k的取值范围;
(2)对于一个函数,当自变量x取a时,函数值y也等于a,我们称a为这个函数的对等值.若函数y=x2+(k﹣5)x+1﹣k有两相异的对等值x1,x2,且x1<2<x2,求k的最大整数值.
解:(1)∵y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,
又a=1>0,△=(k﹣5)2﹣4(1﹣k)=(k﹣3)2+12,
∴抛物线与x轴有两个交点,
设抛物线与x轴交点的横坐标分别为x1,x2,
∴x1+x2=5﹣k>0,x1x2=1﹣k≥0,
解得k≤1,
∴k的取值范围为k≤1;
(2)依题意,得:x2+(k﹣5)x+1﹣k=x,
∴x2+(k﹣6)x+1﹣k=0,
∵△=(k﹣4)2+16>0,
∴k为任意实数,
又x1+x2=6﹣k,x1x2=1﹣k,
∵(x1﹣2)(x2﹣2)<0,
∴x1x2﹣2(x1+x2)+4<0,
∴1﹣k﹣2(6﹣k)+4<0,
∴k<7,
∴综上,k的最大整数值为6.
13.如图,已知抛物线(k为常数,k>0)与x轴从左至右依次交于点A、B,与y轴交于点C,经过点B的直线与抛物线的另一个交点为D.
(1)若点D的横坐标为-5,求抛物线的函数关系式;
(2)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标为多少时,点M在整个运动过程中用时最少?
解:(1)抛物线y=x2﹣x﹣k,
令y=0,解得x=﹣2或x=4,
∴A(﹣2,0),B(4,0).
∵直线y=﹣x+b经过点B(4,0),
∴﹣×4+b=0,解得b=,
∴直线BD解析式为:y=﹣x+.
当x=﹣5时,y=3,
∴D(﹣5,3).
∵点D(﹣5,3)在抛物线y=(x+2)(x﹣4)上,
∴(﹣5+2)(﹣5﹣4)=3,
∴k=.
∴抛物线的函数表达式为:y=(x+2)(x﹣4).
即y=x2﹣x﹣;
(2)如答图3,由(1)知:D(﹣5,3),
如答图2﹣2,过点D作DN⊥x轴于点N,则DN=3,ON=5,BN=4+5=9,
∴tan∠DBA===,
∴∠DBA=30°.
过点D作DK∥x轴,则∠KDF=∠DBA=30°.
过点F作FG⊥DK于点G,则FG=DF.
由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+DF,
∴t=AF+FG,即运动的时间值等于折线AF+FG的长度值.
由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.
过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求之F点.
∵A点横坐标为﹣2,直线BD解析式为:y=﹣x+,
∴y=﹣×(﹣2)+=2,
∴F(﹣2,2).
综上所述,当点F坐标为(﹣2,2)时,点M在整个运动过程中用时最少.
14.如图,矩形ABCD的对角线AC,BD相交于点O,ΔCOD关于CD的对称图形是ΔCED。
(1)求证:四边形OCED是菱形。
(2)连接AE,若AB=6cm,BC=cm。
①求sin∠EAD的值。
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动。当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间。
(1)证明:∵四边形ABCD是矩形.
∴OD=OB=OC=OA,
∵△EDC和△ODC关于CD对称,
∴DE=DO,CE=CO,
∴DE=EC=CO=OD,
∴四边形CODE是菱形.
(2)①设AE交CD于K.
∵四边形CODE是菱形,
∴DE∥AC,DE=OC=OA,
∴==
∵AB=CD=6,
∴DK=2,CK=4,
在Rt△ADK中,AK===3,
∴sin∠DAE==,
②作PF⊥AD于F.易知PF=AP sin∠DAE=AP,
∵点Q的运动时间t=+=OP+AP=OP+PF,
∴当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,
∴OF=CD=3.AF=AD=,PF=DK=1,
∴AP==,
∴当点Q沿上述路线运动到点A所需要的时间最短时,AP的长为cm,点Q走完全程所需的时间为3s.
21世纪教育网(www.21cnjy.com)
同课章节目录
