第三章数据分析初步期中复习(含解析)
文档属性
| 名称 | 第三章数据分析初步期中复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 368.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章数据分析初步期中复习浙教版2024—2025学年八年级下册
一、选择题
1.甲、乙、丙三支女子花样游泳队的人数相同,且平均身高都是1.68m,身高的方差分别是,,,则身高最整齐的游泳队是( )
A.甲 B.乙 C.丙 D.无法确定
2.为深入贯彻落实《中共中央、国务院关于学习运用“千村示范、万村整治”工程经验有力有效推进乡村全面振兴的意见》精神,某镇组织开展“乡村艺术大舞台”活动,其中参赛的六个村得分分别为:88,90,83,95,92,88,则这组数据的中位数是( )
A.88 B.89 C.90 D.91
3.菲尔兹奖是数学领域的一项国际大奖,每四年颁发一次,被誉为“数学界的诺贝尔奖”.截至2022年,世界上共有65位数学家获得菲尔兹奖,获奖者获奖时的年龄分布如下表:
年龄/岁 27 29 31 32 33 34 35 36 37 38 39 40 45
人数 1 3 5 4 4 4 6 5 9 9 7 7 1
则该组由年龄组成的数据的众数是( )
A.9 B.37 C.45 D.37,38
4.中国空间站已全面建成并转入应用与发展阶段,中国载人月球探测工程登月阶段任务已启动实施.为加强学生对我国航天知识的了解,某学校开展了航天知识竞赛,其中8名学生的竞赛成绩为:87,86,89,87,88,90,95,97,则这组数据的众数和中位数分别是( )
A.87,88.5 B.88.5,87 C.87,88 D.88,88
5.已知一组样本数据x1,x2…,xn为不全相等的n个正数,其中n≥4.若把数据x1,x2,…,xn都扩大m倍再减去l(其中m是实数,m≠0),生成一组新的数据mx1﹣l,mx2﹣l,…,mxn﹣l,则这组新数据与原数据相比较,( )
A.平均数相等 B.中位数相等
C.方差相等 D.标准差可能相等
二、填空题
6.某学校把学生的思想素质测试、行为习惯两项成绩分别按60%、40%的比例计入评价总成绩中的一项.小明行为习惯的成绩是81分,若想评价总成绩中这一项不低于90分,则思想素质测试的成绩至少是 分.
7.已知如下的两组数据:
第一组:20,21,22,25,24,23;
第二组:20,21,23,25,a,26.
若两组数据的中位数相等,实数a= .
8.某校举行诵读比赛,比赛得分按形象占30%、内容占30%、效果占40%进行计算.雅韵队这三项得分依次为90,95,92,则雅韵队的最终比赛成绩为 分.
9.一组数据2,1,2,x,3中,唯一的众数是x,这组数据的方差是 .
10.若10个数据x1,x2,x3,…,x10的方差为3,则数据x1+1,x2+1,x3+1,…,x10+1的方差为 .
三、解答题
11.如表是某同学本学期体育素质历次测试成绩(百分制)如表所示:
测试类别 平时测试 期中测试 期末测试
第1次 第2次 第3次
成绩 82 86 87 82 90
(1)该同学本学期五次测试成绩的众数为 ,中位数为 ;
(2)该同学本学期体育素质平时测试的平均成绩为 ;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测试成绩、期末测试成绩按照2:3:5的比例计算所得,求该同学本学期体育素质的总评成绩.
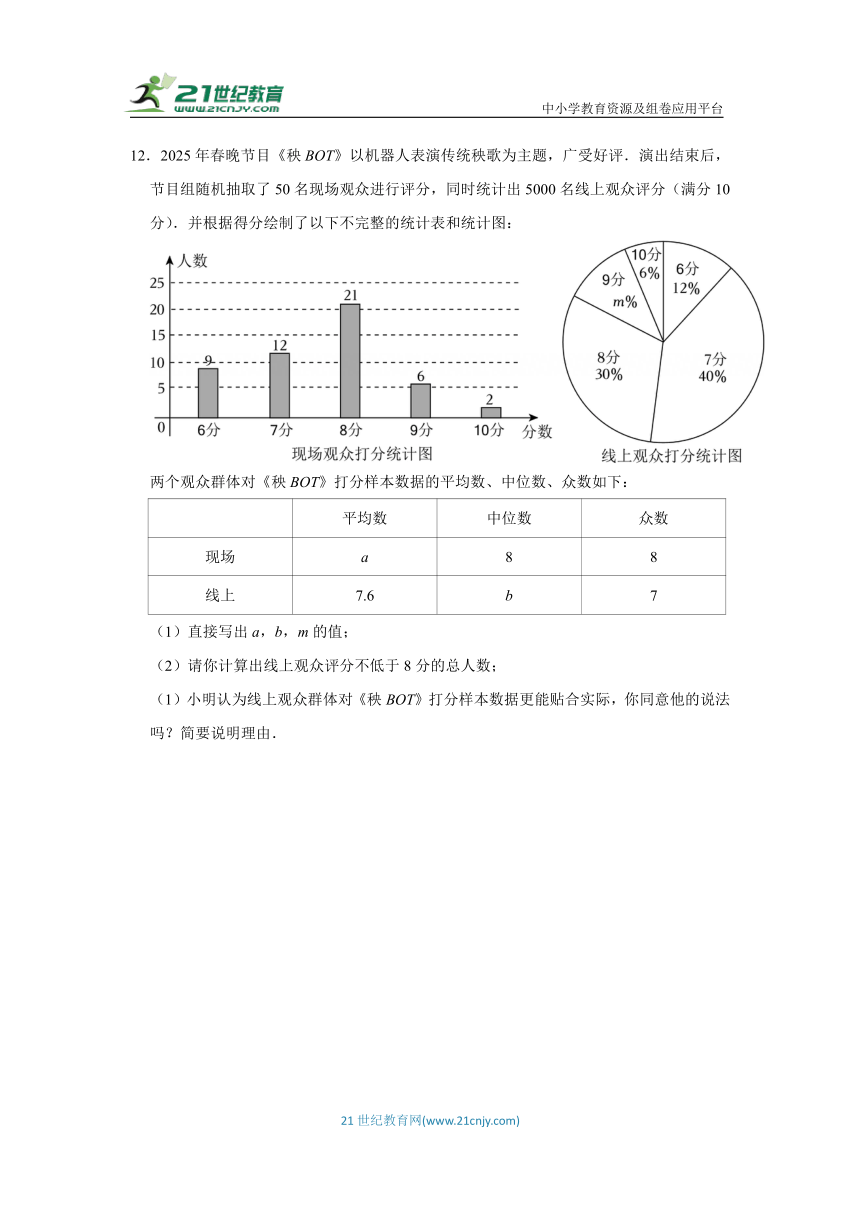
12.2025年春晚节目《秧BOT》以机器人表演传统秧歌为主题,广受好评.演出结束后,节目组随机抽取了50名现场观众进行评分,同时统计出5000名线上观众评分(满分10分).并根据得分绘制了以下不完整的统计表和统计图:
两个观众群体对《秧BOT》打分样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
现场 a 8 8
线上 7.6 b 7
(1)直接写出a,b,m的值;
(2)请你计算出线上观众评分不低于8分的总人数;
(1)小明认为线上观众群体对《秧BOT》打分样本数据更能贴合实际,你同意他的说法吗?简要说明理由.
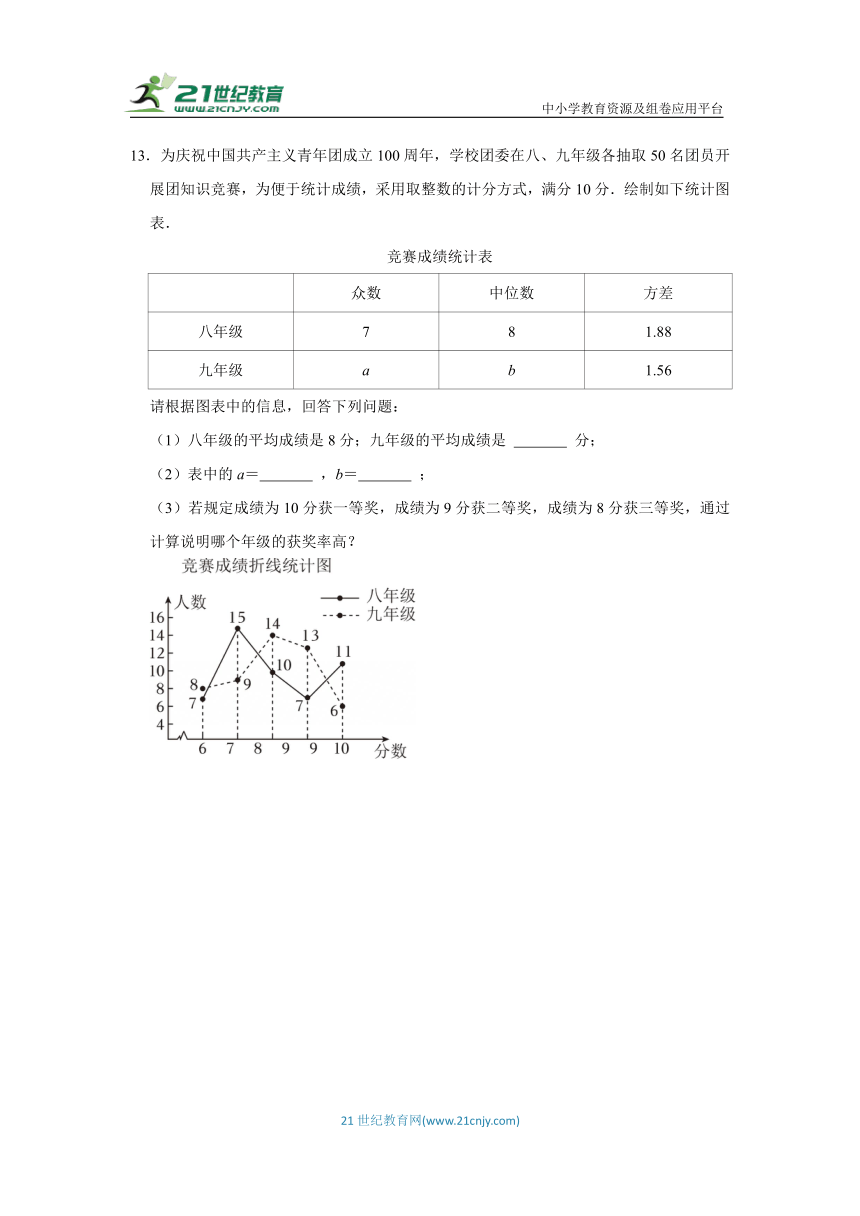
13.为庆祝中国共产主义青年团成立100周年,学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,采用取整数的计分方式,满分10分.绘制如下统计图表.
竞赛成绩统计表
众数 中位数 方差
八年级 7 8 1.88
九年级 a b 1.56
请根据图表中的信息,回答下列问题:
(1)八年级的平均成绩是8分;九年级的平均成绩是 分;
(2)表中的a= ,b= ;
(3)若规定成绩为10分获一等奖,成绩为9分获二等奖,成绩为8分获三等奖,通过计算说明哪个年级的获奖率高?
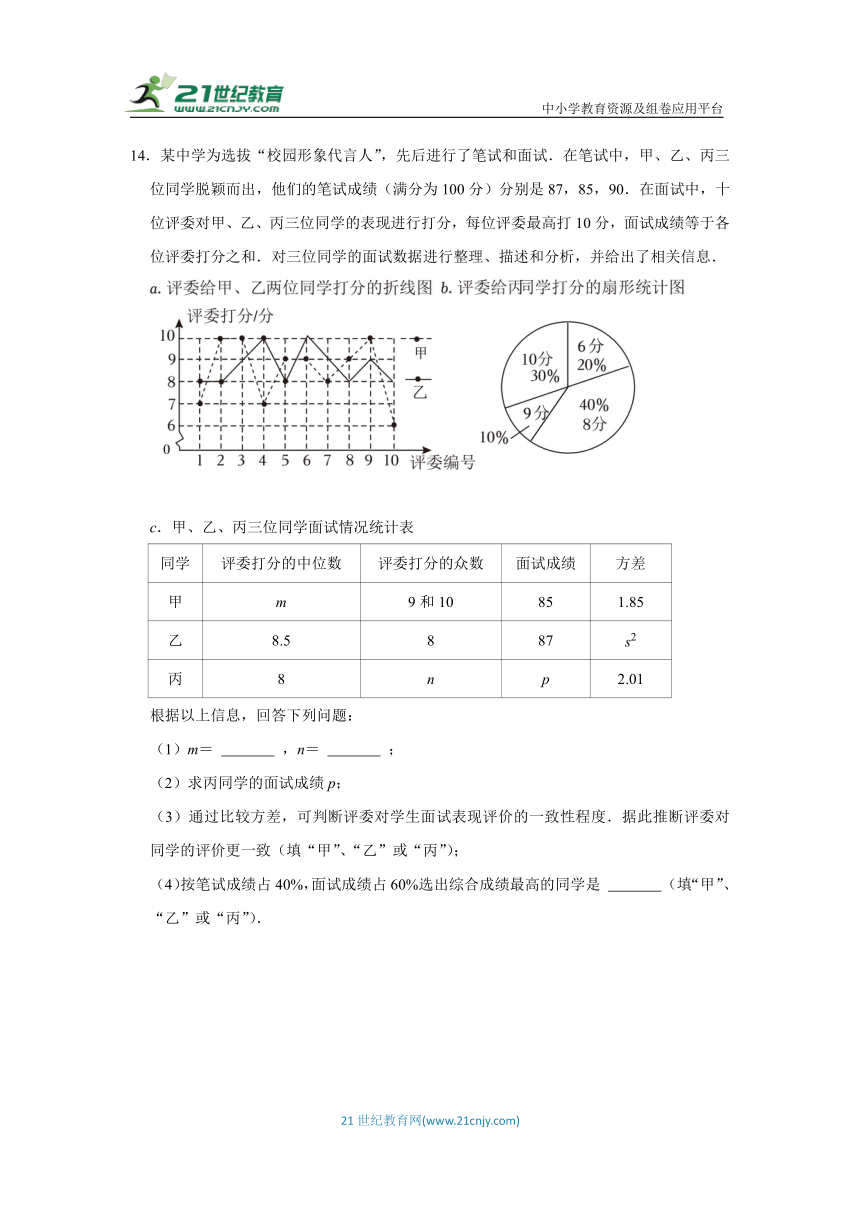
14.某中学为选拔“校园形象代言人”,先后进行了笔试和面试.在笔试中,甲、乙、丙三位同学脱颖而出,他们的笔试成绩(满分为100分)分别是87,85,90.在面试中,十位评委对甲、乙、丙三位同学的表现进行打分,每位评委最高打10分,面试成绩等于各位评委打分之和.对三位同学的面试数据进行整理、描述和分析,并给出了相关信息.
c.甲、乙、丙三位同学面试情况统计表
同学 评委打分的中位数 评委打分的众数 面试成绩 方差
甲 m 9和10 85 1.85
乙 8.5 8 87 s2
丙 8 n p 2.01
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)求丙同学的面试成绩p;
(3)通过比较方差,可判断评委对学生面试表现评价的一致性程度.据此推断评委对 同学的评价更一致(填“甲”、“乙”或“丙”);
(4)按笔试成绩占40%,面试成绩占60%选出综合成绩最高的同学是 (填“甲”、“乙”或“丙”).
15.某校舞蹈队共16名学生,测量并获取了所有学生的身高(单位:cm),数据整理如下:
①16名学生的身高:
161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,173;
②16名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
166.625 m n
(1)写出表中m,n的值:m= ,n= ;
(2)一般认为,如果一组学生的身高比较整齐,则该组舞台呈现效果越好.下面是学校选出的两个舞蹈小组的学生的身高,你认为舞台呈现效果更好的是哪一组?请说明你的理由.
甲组学生的身高 162 165 165 166 167
乙组学生的身高 161 162 164 165 173
参考答案
一、选择题
1.【解答】解:∵,
∴,
则身高最整齐的游泳队是乙,
故选:B.
2.【解答】解:这组数据按照从小到大的顺序排列为:83,88,88,90,92,95,
中位数为89.
故选:B.
3.【解答】解:由表格可知:这一组数据中37,38出现的次数最多,
因此该组由年龄组成的数据的众数是37,38.
故选:D.
4.【解答】解:87出现的次数最多,
所以众数为:87.
数据从小到大排列为:86,87,87,88,89,90,95,97,
所以中位数为: =88.5,
故选:A.
5.【解答】解:A、设原数据的平均数为,
则新数据的平均数为m1,平均数不相等,不符合题意;
B、设原数据的中位数为a,
则新数据的平均数为ma﹣1,中位数不相等,不符合题意;
C、设原数据的方差为S2,
则新数据的方差为m2S2,方差可能相等,也可能不相等,不符合题意;
D、设原数据的标准差为S,
则新数据的标准差为mS,当m=1时,标准差相等,符合题意;
故选:D.
二、填空题
6.【解答】解:设思想素质测试的成绩为x分.
由题意得x 60%+81×40%≥90,
解得x≥96,
∴思想素质测试的成绩至少为9(6分).
故答案为:96.
7.【解答】解:第一组:20,21,22,25,24,23排列后为20,21,22,23,24,25,
∴中位数为(22+23)÷2=22.5,
①第二组排列为:a,20,21,23,25,26,中位数为(21+23)÷2=22,不符合题意;
②第二组排列为:20,a,21,23,25,26,中位数为(21+23)÷2=22,不符合题意;
③第二组排列为:20,21,a,23,25,26,中位数为(a+23)÷2=22.5,解得:a=22;
④第二组排列为:20,21,23,a,25,26,中位数为(a+23)÷2=22.5,解得:a=22,此时a<23,不符合题意;
⑤第二组排列为:20,21,23,25,a,26,中位数为(25+23)÷2=24,不符合题意;
⑥第二组排列为:20,21,23,25,26,a,中位数为(25+23)÷2=24,不符合题意;
故a=22,
故答案为:22.
8.【解答】解:雅韵队的最终比赛成绩为:90×30%+95×30%+92×40%
=27+28.5+36.8
=92.3(分).
故答案为:92.3.
9.【解答】解:因为一组数据2,1,2,x,3有唯一的众数x,所以x=2.于是这组数据为2,1,2,2,3.
该组数据的平均数为:(2+1+2+3+3)=2.
这组数据的方差是s2[(2﹣2)2×3+(1﹣2)2+(3﹣2)2]=0.4.
故答案为:0.4.
10.【解答】解:∵数据x1,x2,x3,…,x10的方差是3,
∴数据x1+1,x2+1,x3+1,…,x10+1的方差为3.
故答案为:3.
三、解答题
11.【解答】解:(1)∵该同学的5次成绩分别为82、86、87、82、90,
∴该同学5次成绩的众数为82,中位数为86,
故答案为:82,86;
(2)(82+86+87)=85,
故答案为:85;
(3)86.6,
即该同学本学期体育素质的总评成绩为86.6.
12.【解答】解:(1)现场打分的平均数a(6×9+7×12+8×21+9×6+10×2)=7.6,线上打分的中位数b=7分,
m%=1﹣(12%+40%+30%+6%)=12%,即m=12;
(2)线上观众评分不低于8分的总人数为5000×(12%+40%+30%)=4100(人);
(3)同意,因为线上观众群体对《秧BOT》打分样本数据样本容量大,更能体现实际情况.
13.【解答】解:(1)九年级的平均成绩(8×6+9×7+14×8+13×9+6×10)=8(分);
故答案为:8;
(2)九年级的成绩的众数为8,中位数为(8+8)=8,
即a=8,b=8,
故答案为:8,8;
(3)八年级的获奖率56%;
九年级的获奖率66%;
所以九年级的获奖率比八年级的获奖率高.
14.【解答】解:(1)把甲的得分从小到大排列,排在中间的两个数分别是9,9,故中位数m9,
由扇形图可知丙的得分(8分)的最多,故众数n=8;
故答案为:9,8;
(2)6×10×20%+8×10×40%+9×10×10%+10×10×30%=83,
答:丙同学的面试成绩p为83;
(3)由题意可知,甲的方差比丙的小,由折线统计图可知乙的得分的波动比甲小,所以评委对乙同学的评价更一致;
故答案为:乙;
(4)甲的综合成绩为:87×40%+85×60%=85.8(分),
乙的综合成绩为:85×40%+87×60%=86.2(分),
丙的综合成绩为:90×40%+83×60%=85.8(分),
86.2>85.8,
所以综合成绩最高的是乙.
故答案为:乙.
15.【解答】解:(1)中位数为m166,
众数为n=165;
故答案为:166,165;
(2)甲组学生身高的平均数是:165(cm),
甲组学生身高的方差为:[(165﹣162)2+2×(165﹣165)2+(165﹣166)2+(165﹣167)2]=2.8,
乙组学生身高的平均数是:165(cm),
乙组学生身高的方差为:[(165﹣161)2+(165﹣162)2+(165﹣164)2+(165﹣165)2+(165﹣173)2]=18,
∵18>2.8,
∴甲组舞台呈现效果更好.
21世纪教育网(www.21cnjy.com)
第三章数据分析初步期中复习浙教版2024—2025学年八年级下册
一、选择题
1.甲、乙、丙三支女子花样游泳队的人数相同,且平均身高都是1.68m,身高的方差分别是,,,则身高最整齐的游泳队是( )
A.甲 B.乙 C.丙 D.无法确定
2.为深入贯彻落实《中共中央、国务院关于学习运用“千村示范、万村整治”工程经验有力有效推进乡村全面振兴的意见》精神,某镇组织开展“乡村艺术大舞台”活动,其中参赛的六个村得分分别为:88,90,83,95,92,88,则这组数据的中位数是( )
A.88 B.89 C.90 D.91
3.菲尔兹奖是数学领域的一项国际大奖,每四年颁发一次,被誉为“数学界的诺贝尔奖”.截至2022年,世界上共有65位数学家获得菲尔兹奖,获奖者获奖时的年龄分布如下表:
年龄/岁 27 29 31 32 33 34 35 36 37 38 39 40 45
人数 1 3 5 4 4 4 6 5 9 9 7 7 1
则该组由年龄组成的数据的众数是( )
A.9 B.37 C.45 D.37,38
4.中国空间站已全面建成并转入应用与发展阶段,中国载人月球探测工程登月阶段任务已启动实施.为加强学生对我国航天知识的了解,某学校开展了航天知识竞赛,其中8名学生的竞赛成绩为:87,86,89,87,88,90,95,97,则这组数据的众数和中位数分别是( )
A.87,88.5 B.88.5,87 C.87,88 D.88,88
5.已知一组样本数据x1,x2…,xn为不全相等的n个正数,其中n≥4.若把数据x1,x2,…,xn都扩大m倍再减去l(其中m是实数,m≠0),生成一组新的数据mx1﹣l,mx2﹣l,…,mxn﹣l,则这组新数据与原数据相比较,( )
A.平均数相等 B.中位数相等
C.方差相等 D.标准差可能相等
二、填空题
6.某学校把学生的思想素质测试、行为习惯两项成绩分别按60%、40%的比例计入评价总成绩中的一项.小明行为习惯的成绩是81分,若想评价总成绩中这一项不低于90分,则思想素质测试的成绩至少是 分.
7.已知如下的两组数据:
第一组:20,21,22,25,24,23;
第二组:20,21,23,25,a,26.
若两组数据的中位数相等,实数a= .
8.某校举行诵读比赛,比赛得分按形象占30%、内容占30%、效果占40%进行计算.雅韵队这三项得分依次为90,95,92,则雅韵队的最终比赛成绩为 分.
9.一组数据2,1,2,x,3中,唯一的众数是x,这组数据的方差是 .
10.若10个数据x1,x2,x3,…,x10的方差为3,则数据x1+1,x2+1,x3+1,…,x10+1的方差为 .
三、解答题
11.如表是某同学本学期体育素质历次测试成绩(百分制)如表所示:
测试类别 平时测试 期中测试 期末测试
第1次 第2次 第3次
成绩 82 86 87 82 90
(1)该同学本学期五次测试成绩的众数为 ,中位数为 ;
(2)该同学本学期体育素质平时测试的平均成绩为 ;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测试成绩、期末测试成绩按照2:3:5的比例计算所得,求该同学本学期体育素质的总评成绩.
12.2025年春晚节目《秧BOT》以机器人表演传统秧歌为主题,广受好评.演出结束后,节目组随机抽取了50名现场观众进行评分,同时统计出5000名线上观众评分(满分10分).并根据得分绘制了以下不完整的统计表和统计图:
两个观众群体对《秧BOT》打分样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
现场 a 8 8
线上 7.6 b 7
(1)直接写出a,b,m的值;
(2)请你计算出线上观众评分不低于8分的总人数;
(1)小明认为线上观众群体对《秧BOT》打分样本数据更能贴合实际,你同意他的说法吗?简要说明理由.
13.为庆祝中国共产主义青年团成立100周年,学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,采用取整数的计分方式,满分10分.绘制如下统计图表.
竞赛成绩统计表
众数 中位数 方差
八年级 7 8 1.88
九年级 a b 1.56
请根据图表中的信息,回答下列问题:
(1)八年级的平均成绩是8分;九年级的平均成绩是 分;
(2)表中的a= ,b= ;
(3)若规定成绩为10分获一等奖,成绩为9分获二等奖,成绩为8分获三等奖,通过计算说明哪个年级的获奖率高?
14.某中学为选拔“校园形象代言人”,先后进行了笔试和面试.在笔试中,甲、乙、丙三位同学脱颖而出,他们的笔试成绩(满分为100分)分别是87,85,90.在面试中,十位评委对甲、乙、丙三位同学的表现进行打分,每位评委最高打10分,面试成绩等于各位评委打分之和.对三位同学的面试数据进行整理、描述和分析,并给出了相关信息.
c.甲、乙、丙三位同学面试情况统计表
同学 评委打分的中位数 评委打分的众数 面试成绩 方差
甲 m 9和10 85 1.85
乙 8.5 8 87 s2
丙 8 n p 2.01
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)求丙同学的面试成绩p;
(3)通过比较方差,可判断评委对学生面试表现评价的一致性程度.据此推断评委对 同学的评价更一致(填“甲”、“乙”或“丙”);
(4)按笔试成绩占40%,面试成绩占60%选出综合成绩最高的同学是 (填“甲”、“乙”或“丙”).
15.某校舞蹈队共16名学生,测量并获取了所有学生的身高(单位:cm),数据整理如下:
①16名学生的身高:
161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,173;
②16名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
166.625 m n
(1)写出表中m,n的值:m= ,n= ;
(2)一般认为,如果一组学生的身高比较整齐,则该组舞台呈现效果越好.下面是学校选出的两个舞蹈小组的学生的身高,你认为舞台呈现效果更好的是哪一组?请说明你的理由.
甲组学生的身高 162 165 165 166 167
乙组学生的身高 161 162 164 165 173
参考答案
一、选择题
1.【解答】解:∵,
∴,
则身高最整齐的游泳队是乙,
故选:B.
2.【解答】解:这组数据按照从小到大的顺序排列为:83,88,88,90,92,95,
中位数为89.
故选:B.
3.【解答】解:由表格可知:这一组数据中37,38出现的次数最多,
因此该组由年龄组成的数据的众数是37,38.
故选:D.
4.【解答】解:87出现的次数最多,
所以众数为:87.
数据从小到大排列为:86,87,87,88,89,90,95,97,
所以中位数为: =88.5,
故选:A.
5.【解答】解:A、设原数据的平均数为,
则新数据的平均数为m1,平均数不相等,不符合题意;
B、设原数据的中位数为a,
则新数据的平均数为ma﹣1,中位数不相等,不符合题意;
C、设原数据的方差为S2,
则新数据的方差为m2S2,方差可能相等,也可能不相等,不符合题意;
D、设原数据的标准差为S,
则新数据的标准差为mS,当m=1时,标准差相等,符合题意;
故选:D.
二、填空题
6.【解答】解:设思想素质测试的成绩为x分.
由题意得x 60%+81×40%≥90,
解得x≥96,
∴思想素质测试的成绩至少为9(6分).
故答案为:96.
7.【解答】解:第一组:20,21,22,25,24,23排列后为20,21,22,23,24,25,
∴中位数为(22+23)÷2=22.5,
①第二组排列为:a,20,21,23,25,26,中位数为(21+23)÷2=22,不符合题意;
②第二组排列为:20,a,21,23,25,26,中位数为(21+23)÷2=22,不符合题意;
③第二组排列为:20,21,a,23,25,26,中位数为(a+23)÷2=22.5,解得:a=22;
④第二组排列为:20,21,23,a,25,26,中位数为(a+23)÷2=22.5,解得:a=22,此时a<23,不符合题意;
⑤第二组排列为:20,21,23,25,a,26,中位数为(25+23)÷2=24,不符合题意;
⑥第二组排列为:20,21,23,25,26,a,中位数为(25+23)÷2=24,不符合题意;
故a=22,
故答案为:22.
8.【解答】解:雅韵队的最终比赛成绩为:90×30%+95×30%+92×40%
=27+28.5+36.8
=92.3(分).
故答案为:92.3.
9.【解答】解:因为一组数据2,1,2,x,3有唯一的众数x,所以x=2.于是这组数据为2,1,2,2,3.
该组数据的平均数为:(2+1+2+3+3)=2.
这组数据的方差是s2[(2﹣2)2×3+(1﹣2)2+(3﹣2)2]=0.4.
故答案为:0.4.
10.【解答】解:∵数据x1,x2,x3,…,x10的方差是3,
∴数据x1+1,x2+1,x3+1,…,x10+1的方差为3.
故答案为:3.
三、解答题
11.【解答】解:(1)∵该同学的5次成绩分别为82、86、87、82、90,
∴该同学5次成绩的众数为82,中位数为86,
故答案为:82,86;
(2)(82+86+87)=85,
故答案为:85;
(3)86.6,
即该同学本学期体育素质的总评成绩为86.6.
12.【解答】解:(1)现场打分的平均数a(6×9+7×12+8×21+9×6+10×2)=7.6,线上打分的中位数b=7分,
m%=1﹣(12%+40%+30%+6%)=12%,即m=12;
(2)线上观众评分不低于8分的总人数为5000×(12%+40%+30%)=4100(人);
(3)同意,因为线上观众群体对《秧BOT》打分样本数据样本容量大,更能体现实际情况.
13.【解答】解:(1)九年级的平均成绩(8×6+9×7+14×8+13×9+6×10)=8(分);
故答案为:8;
(2)九年级的成绩的众数为8,中位数为(8+8)=8,
即a=8,b=8,
故答案为:8,8;
(3)八年级的获奖率56%;
九年级的获奖率66%;
所以九年级的获奖率比八年级的获奖率高.
14.【解答】解:(1)把甲的得分从小到大排列,排在中间的两个数分别是9,9,故中位数m9,
由扇形图可知丙的得分(8分)的最多,故众数n=8;
故答案为:9,8;
(2)6×10×20%+8×10×40%+9×10×10%+10×10×30%=83,
答:丙同学的面试成绩p为83;
(3)由题意可知,甲的方差比丙的小,由折线统计图可知乙的得分的波动比甲小,所以评委对乙同学的评价更一致;
故答案为:乙;
(4)甲的综合成绩为:87×40%+85×60%=85.8(分),
乙的综合成绩为:85×40%+87×60%=86.2(分),
丙的综合成绩为:90×40%+83×60%=85.8(分),
86.2>85.8,
所以综合成绩最高的是乙.
故答案为:乙.
15.【解答】解:(1)中位数为m166,
众数为n=165;
故答案为:166,165;
(2)甲组学生身高的平均数是:165(cm),
甲组学生身高的方差为:[(165﹣162)2+2×(165﹣165)2+(165﹣166)2+(165﹣167)2]=2.8,
乙组学生身高的平均数是:165(cm),
乙组学生身高的方差为:[(165﹣161)2+(165﹣162)2+(165﹣164)2+(165﹣165)2+(165﹣173)2]=18,
∵18>2.8,
∴甲组舞台呈现效果更好.
21世纪教育网(www.21cnjy.com)
同课章节目录
