第五章特殊平行四边形章节期末复习(含解析)
文档属性
| 名称 | 第五章特殊平行四边形章节期末复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 896.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 07:43:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章特殊平行四边形章节期末复习浙教版2024—2025学年八年级下册
一、选择题
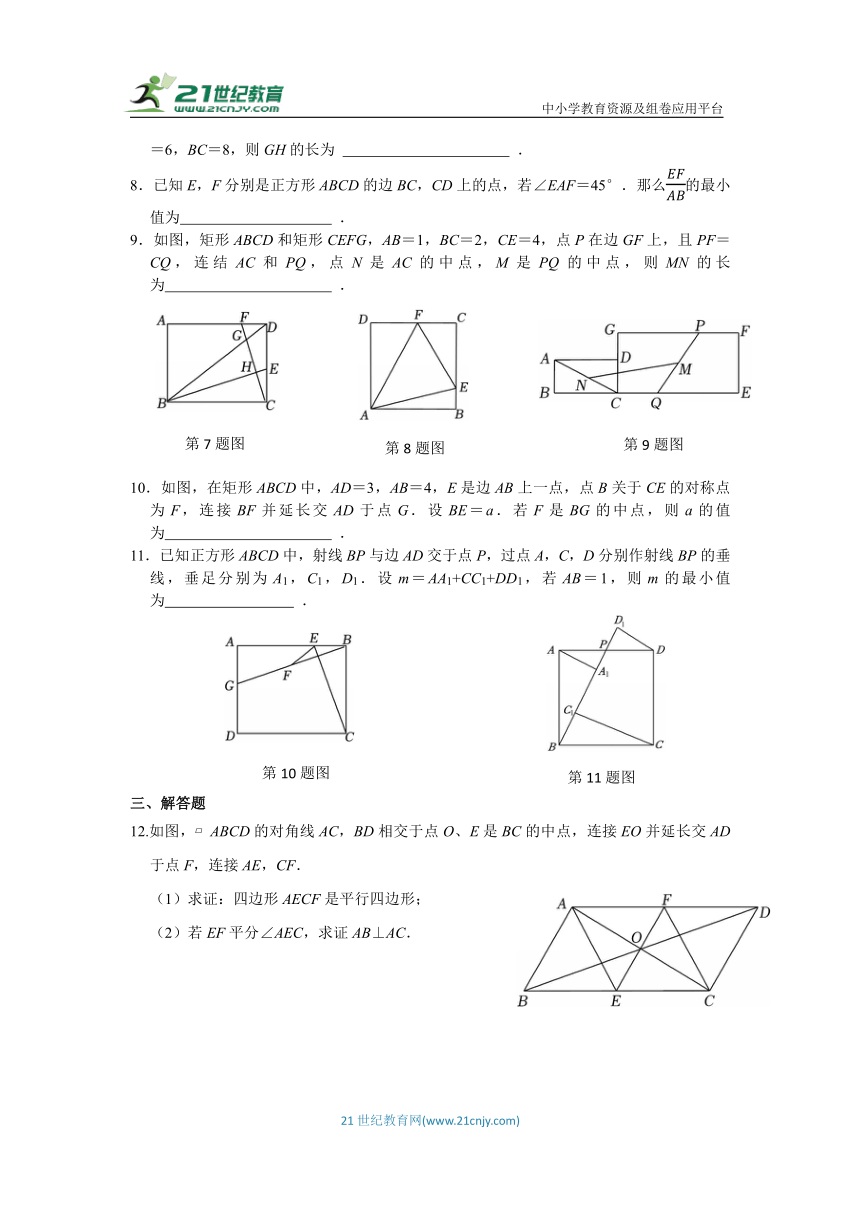
1.如图,在矩形ABCD中,AB=3,AD=4,对角线AC,BD相交于点O,点H为射线BA延长线上一点,连接OH交AD于点E,若AH=1,则OH的长度为( )
A. B. C. D.
2.如图,在边长为的正方形ABCD中,E,F分别是边AB,BC的中点,连接EC,FD,G,H分别是EC,FD的中点,连接GH,则GH的长为( )
A.2.4 B.2.5 C. D.2
3.如图,直线a∥b,矩形ABCD的顶点A、D分别在直线b、a上,若∠2=41°,则∠1的度数为( )
A.41° B.51° C.49° D.59°
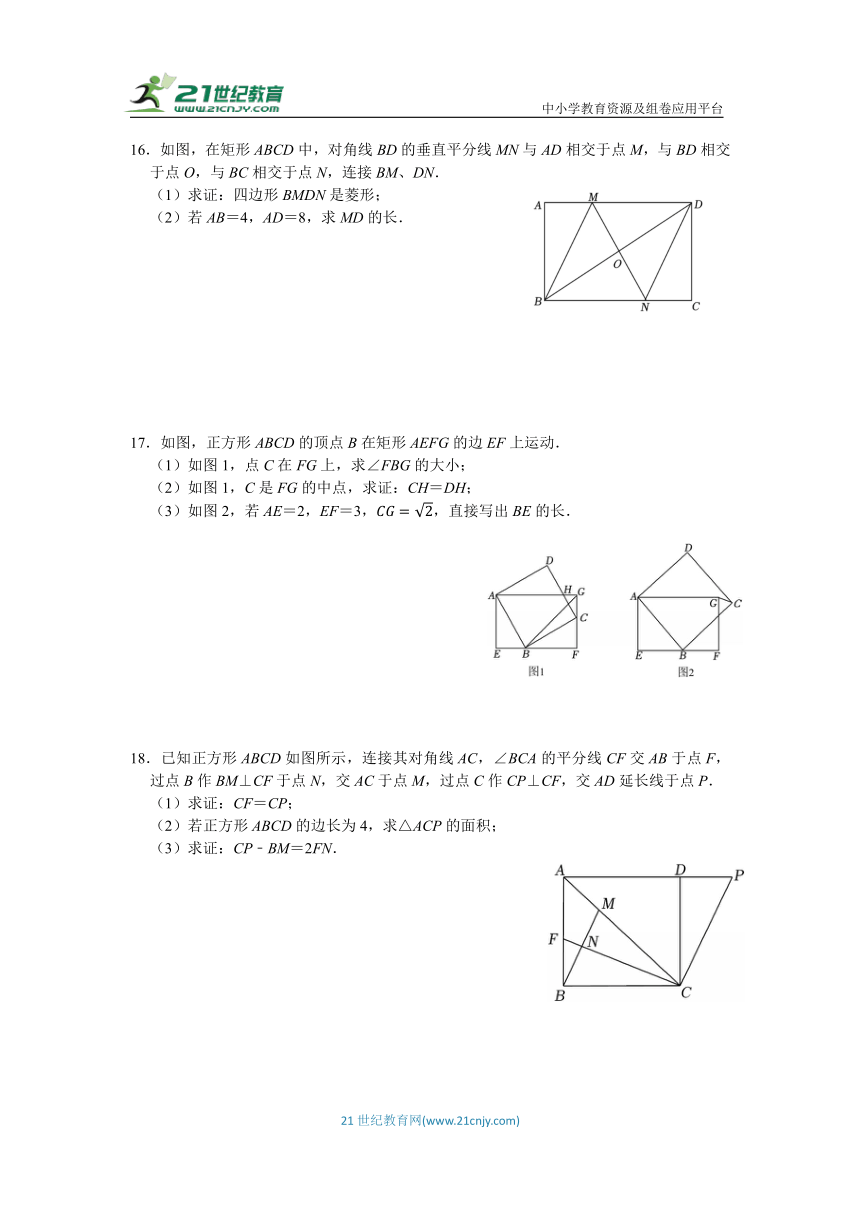
4.如图所示,菱形ABCD的对角线AC、BD相交于点O,若AC=6,BD=8,AE⊥BC,垂足为E,则AE的长为( )
A.2.4 B.4 C.4.8 D.5
5.如图,在正方形ABCD中,点P是对角线BD上一点(点P不与B、D重合),连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF,AF交BD于点G,给出四个结论:①AB2+BF2=2AP2;②BF+DE=EF;③;④;上述结论中,所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②④
6.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
二、填空题
7.如图,在矩形ABCD中,BE平分∠CBD,CF⊥BE,分别交BD,BE于点G,H.若AB=6,BC=8,则GH的长为 .
8.已知E,F分别是正方形ABCD的边BC,CD上的点,若∠EAF=45°.那么的最小值为 .
9.如图,矩形ABCD和矩形CEFG,AB=1,BC=2,CE=4,点P在边GF上,且PF=CQ,连结AC和PQ,点N是AC的中点,M是PQ的中点,则MN的长为 .
10.如图,在矩形ABCD中,AD=3,AB=4,E是边AB上一点,点B关于CE的对称点为F,连接BF并延长交AD于点G.设BE=a.若F是BG的中点,则a的值为 .
11.已知正方形ABCD中,射线BP与边AD交于点P,过点A,C,D分别作射线BP的垂线,垂足分别为A1,C1,D1.设m=AA1+CC1+DD1,若AB=1,则m的最小值为 .
三、解答题
12.如图, ABCD的对角线AC,BD相交于点O、E是BC的中点,连接EO并延长交AD于点F,连接AE,CF.
(1)求证:四边形AECF是平行四边形;
(2)若EF平分∠AEC,求证AB⊥AC.
13.在矩形ABCD中,BD为矩形对角线,E在AD边上,连接EC.
(1)如图1,若∠DCE=45°,BC=CE,CD=1,求BD;
(2)如图2,CF⊥EC,CF=CD,连接BF交EC于H,当H为BF的中点时,求证:DE=2HC.
14.在 ABCD中,点E,F分别在边AD,BC上,连接EF.CE,DF相交于点O,ED=EF,OE=OC.
(1)求证:四边形CDEF是菱形;
(2)若 ABCD的周长为22,BF=1,∠ABC=60°,求CE的长.
15.如图, ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.
(1)求证: ABCD是菱形;
(2)若AB=4,∠ABC=60°,求AE的长.
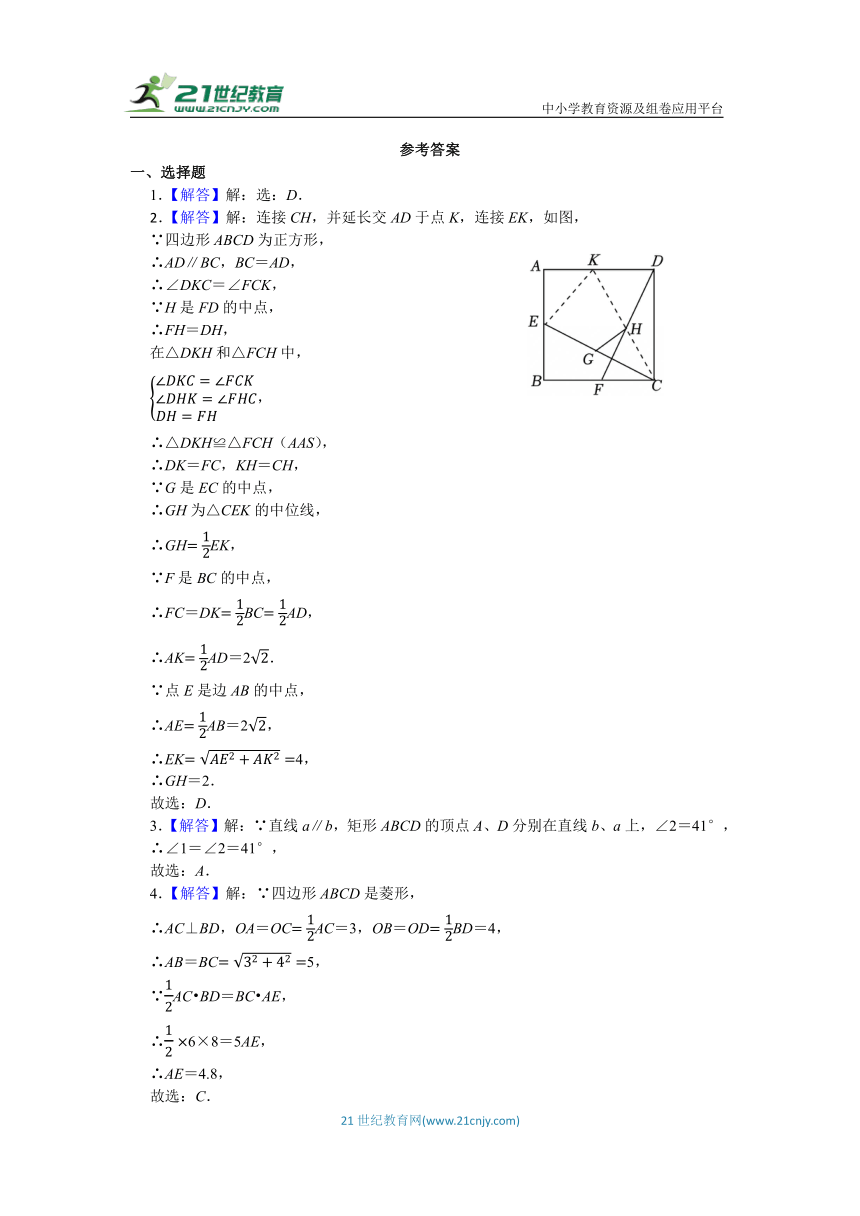
16.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
17.如图,正方形ABCD的顶点B在矩形AEFG的边EF上运动.
(1)如图1,点C在FG上,求∠FBG的大小;
(2)如图1,C是FG的中点,求证:CH=DH;
(3)如图2,若AE=2,EF=3,,直接写出BE的长.
18.已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.
(1)求证:CF=CP;
(2)若正方形ABCD的边长为4,求△ACP的面积;
(3)求证:CP﹣BM=2FN.
参考答案
一、选择题
1.【解答】解:选:D.
2.【解答】解:连接CH,并延长交AD于点K,连接EK,如图,
∵四边形ABCD为正方形,
∴AD∥BC,BC=AD,
∴∠DKC=∠FCK,
∵H是FD的中点,
∴FH=DH,
在△DKH和△FCH中,
,
∴△DKH≌△FCH(AAS),
∴DK=FC,KH=CH,
∵G是EC的中点,
∴GH为△CEK的中位线,
∴GHEK,
∵F是BC的中点,
∴FC=DKBCAD,
∴AKAD=2.
∵点E是边AB的中点,
∴AEAB=2,
∴EK4,
∴GH=2.
故选:D.
3.【解答】解:∵直线a∥b,矩形ABCD的顶点A、D分别在直线b、a上,∠2=41°,
∴∠1=∠2=41°,
故选:A.
4.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OCAC=3,OB=ODBD=4,
∴AB=BC5,
∵AC BD=BC AE,
∴6×8=5AE,
∴AE=4.8,
故选:C.
5.【解答】解:选:C.
6.【解答】解:连接AP,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=62+82=100,BC2=102=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∴当AP⊥BC时,AP有最小值,即EF有最小值,
∵△ABC的面积=BC AP=AB AC,
∴BC AP=AB AC,
∴10AP=6×8,
∴AP=,
∴AP=EF=,
∴EF的最小值为,
故选:C.
二、填空题
7.【解答】解:连接GE,如图所示:
∵四边形ABCD是矩形,且AB=6,BC=8,
∴CD=AB=8,∠BCD=90°,
在Rt△BCD中,由勾股定理得:BD10,
∵BE平分∠CBD,
∴∠CBH=∠GBH,
∵CF⊥BE,
∴∠BHC=∠BHG=90°,
在△BHC和△BHG中,
,
∴△BHC≌△BHG(ASA),
∴BC=BG=8,
∴GD=BD﹣BG=10﹣8=2,
在△BCE和△BGE中,
,
△BCE≌△BGE(SAS),
∴EC=EG,∠BCD=∠BGE=90°,
即EG⊥BD,
设EG=a,则EC=EG=a,
∴DE=CD﹣EC=6﹣a,
在Rt△GDE中,由勾股定理得:GD2+EG2=DE2,
∴22+a2=(6﹣a)2,
解得:,
∴EG,
在Rt△BGE中,由勾股定理得:BE,
由三角形的面积公式得:S△BGEBE GHBG EG,
∴BE GH=BG EG,
∴,
∴GH.
故答案为:.
8.【解答】解:如图,延长CB至点G使BG=DF,连接AG.
∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABG=90°.
又∵DF=BG,
∴△ADF≌△ABG(ASA).
∴∠DAF=∠BAG,AF=AG.
∵∠EAF=45°,
∴∠DAF+∠BAE=90°﹣∠EAF=45°.
∴∠BAG+∠BAE=45°,即∠EAG=45°.
∴∠EAF=∠EAG.
∴△EAF≌△GAF(SAS).
∴EF=GF.
设AB=1,BE=a,DF=b,
∴EF=a+b.
在Rt△ECF中,EC2+CF2=EF2,
∴(a+b)2=(1﹣b)2+(1﹣a)2.
∴a+b+ab﹣1=0.
令mEF=a+b,
∴b=m﹣a.
∴m+a(m﹣a)﹣1=0.
∴a2﹣ma﹣m+1=0.
∵BE存在,
∴a有实数解.
∴Δ≥0.
∴Δ=m2﹣4(﹣m+1)=m2+4m﹣4=(m+2)2﹣8≥0.
∵m>0,
∴m≥22.
∴的最小值为22.
故答案为:22.
9.【解答】解:如图,连接CM,FM,
∵四边形CEFG是矩形,
∴CE∥FG,
∴∠FPM=∠CQM,
∵PF=CQ,∠FPM=∠CQM,PM=QM,
∴△FPM≌△CQM(SAS),
∴∠PMF=∠QMC,FM=CM,
∴P、M、Q三点共线,M为CF的中点,
如图,连接DM并延长交EF于H,连接BD、BH,
∵矩形ABCD和矩形CEFG,
∴CD=AB=1CG,D为CG的中点,N为BD的中点,
∴DM是△CFG的中位线,
∴DM∥GF,DMGF,
∴四边形DGFH是矩形,
∴DMGFDH,M为DH的中点,
∴MN为△BDH的中位线,
∴MNBH,
∵BE=BC+CE=6,EH=1,
由勾股定理得,BH,
∴MN,
故答案为:.
10.【解答】解:∵四边形ABCD是矩形,
∴∠GAB=∠EBC=90°,
∴∠ABG+∠AGB=90°,
由对称的性质得,∠ABG+∠BEC=90°,
∴∠BEC=∠AGB,
∴△GAB∽△EBC,
∴,即,
∴AGa,
如图,过点F作FM⊥AB于点M,则∠EMF=90°,
∵点F是BG的中点,HF⊥AD于点H,
∴四边形AHFM是矩形,AHAGa,HFAB=2,
∴AM=HF=2,MF=AHa,
∴ME=2﹣a,
由对称得,EB=EF=a,
在Rt△MEF中,EM2+FM2=EF2,
∴(2﹣a)2+(a)2=a2,
解得:a或a(舍),
故答案为:.
11.【解答】解:连接BD,PC,
S正方形ABCD=1×1=1,
由勾股定理得:,
∵AB=1,
∴,
∴,
∵,
∴,
∵,
当时,m=AA1+CC1+DD1有最小值,
故答案为:.
三、解答题
12.【解答】证明:(1)在平行四边形ABCD中,AO=CO,AD∥BC,
∴∠FAO=∠ECO,
在△AOF和△CEO中,
,
∴△AOF≌△CEO(ASA),
∴AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)∵AF∥CE,
∴∠AFE=∠CEF,
∵EF平分∠AEC,
∴∠AEF=∠CEF,
∴∠AFE=∠AEF,
∴AE=AF,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,
∴AC⊥EF,
∵点E是BC的中点,
∴BE=CE,
∴BE=AF,
∵BE∥AF,
∴四边形ABEF是平行四边形,
∴AB∥EF,
∴AB⊥AC.
13.【解答】(1)解:∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,
∵∠DCE=45°,
∴∠DEC=∠DCE=45°,
∴ED=CD=1,
∴BC=CECD,
∴BD,
∴BD的长是.
(2)证明:如图2,作DP⊥CE于点P,则∠CDE=∠BPC=90°,
∵CF⊥EC,
∴∠FCH=∠BPH=90°,
∵AD∥CB,
∴∠DEC=∠PCB,
∵H为BF的中点,
∴FH=BH,
在△CHF和△PHB中,
,
∴△CHF≌△PHB(AAS),
∴CF=PB,HC=HP,
∴PC=2HC,
∵CF=CD,
∴CD=PB,
在△DEC和△PCB中,
,
∴△DEC≌△PCB(AAS),
∴DE=PC,
∴DE=2HC.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴ED∥FC,
∴∠EDO=∠CFO,
又∵OC=OE,
∵∠EOD=∠COF,
∴△EOD≌△COF(AAS),
∴ED=FC,
∴四边形CDEF是平行四边形,
又∵ED=EF,
∴四边形CDEF是菱形;
(2)解:∵四边形ABCD是平行四边形,四边形CDEF是菱形,
∴AD=BC,ED=FC,FC=FE,
∴AD﹣ED=BC﹣FC,
∴AE=BF=1,
∵ ABCD的周长为22,
∴,
又∵∠ABC=60°,
∴△EFC是等边三角形,
∴CE=EF=5.
15.【解答】(1)证明:∵DE∥AC,DE=OC,
∴四边形OCED是平行四边形.
∵OE=CD,
∴平行四边形OCED是矩形,
∴∠COD=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,CD=AB=BC=4,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴OA=OC=2,
在Rt△OCD中,由勾股定理得:OD2,
由(1)可知,四边形OCED是矩形,
∴CE=OD=2,∠OCE=90°,
∴AE2,
即AE的长为2.
16.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
17.【解答】解:(1)∵四边形ABCD是正方形,四边形AEFG是矩形,
∴AB=BC,AE=GF,∠E=∠F=∠ABC=90°.
又∵∠EBA+∠FBC=∠BCF+∠FBC=90°,
∴∠EBA=∠BCF.
∴△AEB≌△BFC(AAS).
∴AE=BF.
∴GF=BF.
∴∠FBG=∠BGF=45°;
(2)证明:如图1,分别延长AG与BC交于点P.
∵∠PGC=∠BFC=90°,CG=FC,∠PCG=∠BCF,
∴△PCG≌△BCF,
∴PC=BC.
∵AD=BC,
∴AD=PC.
又∵∠ADH=∠PCH=90°,∠AHD=∠PHC,
∴△ADH≌△PCH(AAS).
∴DH=CH.
(3)解:过点C作CM⊥FG于点M,作CN⊥EF于点N,连CG,
则四边形CMFN为矩形,
由(1)可得△AEB≌△BNC,
∴BN=AE=2,CN=BE,
设:CN=BE=x
则:CM=FN=|2﹣3+x|=|x﹣1|,FM=CN=x,
∴GM=|2﹣x|
在Rt△GMC中,
GC2=MC2+MG2=(x﹣1)2+(2﹣x)2=2,
解得:或.
∴或.
18.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠CAD=∠ACD=45°,
∵CP⊥CF,
∴∠FCP=90°=∠BCD,
∴∠BCF=∠DCP,
∵CD=CB,∠CBF=∠CDP=90°,
∴△CDP≌△CBF(ASA),
∴CF=CP;
(2)∵CF平分∠ACB,
∴∠ACF=∠BCF=22.5°,
∴∠BFC=67.5°,
∵△CDP≌△CBF,
∴∠P=∠BFC=67.5°,且∠CAP=45°,
∴∠ACP=∠P=67.5°,
∴AC=AP,
∵ACAB=4,
∴S△ACPAP×CD=8;
(3)在CN上截取NH=FN,连接BH,
∵△CDP≌△CBF,
∴CP=CF,
∵FN=NH,且BN⊥FH,
∴BH=BF,
∴∠BFH=∠BHF=67.5°,
∴∠FBN=∠HBN=∠BCH=22.5°,
∴∠HBC=∠BAM=45°,
∵AB=BC,∠ABM=∠BCH,
∴△AMB≌△BHC(ASA),
∴CH=BM,
∴CF=BM+2FN,
∴CP﹣BM=2FN.
21世纪教育网(www.21cnjy.com)
第五章特殊平行四边形章节期末复习浙教版2024—2025学年八年级下册
一、选择题
1.如图,在矩形ABCD中,AB=3,AD=4,对角线AC,BD相交于点O,点H为射线BA延长线上一点,连接OH交AD于点E,若AH=1,则OH的长度为( )
A. B. C. D.
2.如图,在边长为的正方形ABCD中,E,F分别是边AB,BC的中点,连接EC,FD,G,H分别是EC,FD的中点,连接GH,则GH的长为( )
A.2.4 B.2.5 C. D.2
3.如图,直线a∥b,矩形ABCD的顶点A、D分别在直线b、a上,若∠2=41°,则∠1的度数为( )
A.41° B.51° C.49° D.59°
4.如图所示,菱形ABCD的对角线AC、BD相交于点O,若AC=6,BD=8,AE⊥BC,垂足为E,则AE的长为( )
A.2.4 B.4 C.4.8 D.5
5.如图,在正方形ABCD中,点P是对角线BD上一点(点P不与B、D重合),连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF,AF交BD于点G,给出四个结论:①AB2+BF2=2AP2;②BF+DE=EF;③;④;上述结论中,所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②④
6.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
二、填空题
7.如图,在矩形ABCD中,BE平分∠CBD,CF⊥BE,分别交BD,BE于点G,H.若AB=6,BC=8,则GH的长为 .
8.已知E,F分别是正方形ABCD的边BC,CD上的点,若∠EAF=45°.那么的最小值为 .
9.如图,矩形ABCD和矩形CEFG,AB=1,BC=2,CE=4,点P在边GF上,且PF=CQ,连结AC和PQ,点N是AC的中点,M是PQ的中点,则MN的长为 .
10.如图,在矩形ABCD中,AD=3,AB=4,E是边AB上一点,点B关于CE的对称点为F,连接BF并延长交AD于点G.设BE=a.若F是BG的中点,则a的值为 .
11.已知正方形ABCD中,射线BP与边AD交于点P,过点A,C,D分别作射线BP的垂线,垂足分别为A1,C1,D1.设m=AA1+CC1+DD1,若AB=1,则m的最小值为 .
三、解答题
12.如图, ABCD的对角线AC,BD相交于点O、E是BC的中点,连接EO并延长交AD于点F,连接AE,CF.
(1)求证:四边形AECF是平行四边形;
(2)若EF平分∠AEC,求证AB⊥AC.
13.在矩形ABCD中,BD为矩形对角线,E在AD边上,连接EC.
(1)如图1,若∠DCE=45°,BC=CE,CD=1,求BD;
(2)如图2,CF⊥EC,CF=CD,连接BF交EC于H,当H为BF的中点时,求证:DE=2HC.
14.在 ABCD中,点E,F分别在边AD,BC上,连接EF.CE,DF相交于点O,ED=EF,OE=OC.
(1)求证:四边形CDEF是菱形;
(2)若 ABCD的周长为22,BF=1,∠ABC=60°,求CE的长.
15.如图, ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.
(1)求证: ABCD是菱形;
(2)若AB=4,∠ABC=60°,求AE的长.
16.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
17.如图,正方形ABCD的顶点B在矩形AEFG的边EF上运动.
(1)如图1,点C在FG上,求∠FBG的大小;
(2)如图1,C是FG的中点,求证:CH=DH;
(3)如图2,若AE=2,EF=3,,直接写出BE的长.
18.已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.
(1)求证:CF=CP;
(2)若正方形ABCD的边长为4,求△ACP的面积;
(3)求证:CP﹣BM=2FN.
参考答案
一、选择题
1.【解答】解:选:D.
2.【解答】解:连接CH,并延长交AD于点K,连接EK,如图,
∵四边形ABCD为正方形,
∴AD∥BC,BC=AD,
∴∠DKC=∠FCK,
∵H是FD的中点,
∴FH=DH,
在△DKH和△FCH中,
,
∴△DKH≌△FCH(AAS),
∴DK=FC,KH=CH,
∵G是EC的中点,
∴GH为△CEK的中位线,
∴GHEK,
∵F是BC的中点,
∴FC=DKBCAD,
∴AKAD=2.
∵点E是边AB的中点,
∴AEAB=2,
∴EK4,
∴GH=2.
故选:D.
3.【解答】解:∵直线a∥b,矩形ABCD的顶点A、D分别在直线b、a上,∠2=41°,
∴∠1=∠2=41°,
故选:A.
4.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OCAC=3,OB=ODBD=4,
∴AB=BC5,
∵AC BD=BC AE,
∴6×8=5AE,
∴AE=4.8,
故选:C.
5.【解答】解:选:C.
6.【解答】解:连接AP,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=62+82=100,BC2=102=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∴当AP⊥BC时,AP有最小值,即EF有最小值,
∵△ABC的面积=BC AP=AB AC,
∴BC AP=AB AC,
∴10AP=6×8,
∴AP=,
∴AP=EF=,
∴EF的最小值为,
故选:C.
二、填空题
7.【解答】解:连接GE,如图所示:
∵四边形ABCD是矩形,且AB=6,BC=8,
∴CD=AB=8,∠BCD=90°,
在Rt△BCD中,由勾股定理得:BD10,
∵BE平分∠CBD,
∴∠CBH=∠GBH,
∵CF⊥BE,
∴∠BHC=∠BHG=90°,
在△BHC和△BHG中,
,
∴△BHC≌△BHG(ASA),
∴BC=BG=8,
∴GD=BD﹣BG=10﹣8=2,
在△BCE和△BGE中,
,
△BCE≌△BGE(SAS),
∴EC=EG,∠BCD=∠BGE=90°,
即EG⊥BD,
设EG=a,则EC=EG=a,
∴DE=CD﹣EC=6﹣a,
在Rt△GDE中,由勾股定理得:GD2+EG2=DE2,
∴22+a2=(6﹣a)2,
解得:,
∴EG,
在Rt△BGE中,由勾股定理得:BE,
由三角形的面积公式得:S△BGEBE GHBG EG,
∴BE GH=BG EG,
∴,
∴GH.
故答案为:.
8.【解答】解:如图,延长CB至点G使BG=DF,连接AG.
∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABG=90°.
又∵DF=BG,
∴△ADF≌△ABG(ASA).
∴∠DAF=∠BAG,AF=AG.
∵∠EAF=45°,
∴∠DAF+∠BAE=90°﹣∠EAF=45°.
∴∠BAG+∠BAE=45°,即∠EAG=45°.
∴∠EAF=∠EAG.
∴△EAF≌△GAF(SAS).
∴EF=GF.
设AB=1,BE=a,DF=b,
∴EF=a+b.
在Rt△ECF中,EC2+CF2=EF2,
∴(a+b)2=(1﹣b)2+(1﹣a)2.
∴a+b+ab﹣1=0.
令mEF=a+b,
∴b=m﹣a.
∴m+a(m﹣a)﹣1=0.
∴a2﹣ma﹣m+1=0.
∵BE存在,
∴a有实数解.
∴Δ≥0.
∴Δ=m2﹣4(﹣m+1)=m2+4m﹣4=(m+2)2﹣8≥0.
∵m>0,
∴m≥22.
∴的最小值为22.
故答案为:22.
9.【解答】解:如图,连接CM,FM,
∵四边形CEFG是矩形,
∴CE∥FG,
∴∠FPM=∠CQM,
∵PF=CQ,∠FPM=∠CQM,PM=QM,
∴△FPM≌△CQM(SAS),
∴∠PMF=∠QMC,FM=CM,
∴P、M、Q三点共线,M为CF的中点,
如图,连接DM并延长交EF于H,连接BD、BH,
∵矩形ABCD和矩形CEFG,
∴CD=AB=1CG,D为CG的中点,N为BD的中点,
∴DM是△CFG的中位线,
∴DM∥GF,DMGF,
∴四边形DGFH是矩形,
∴DMGFDH,M为DH的中点,
∴MN为△BDH的中位线,
∴MNBH,
∵BE=BC+CE=6,EH=1,
由勾股定理得,BH,
∴MN,
故答案为:.
10.【解答】解:∵四边形ABCD是矩形,
∴∠GAB=∠EBC=90°,
∴∠ABG+∠AGB=90°,
由对称的性质得,∠ABG+∠BEC=90°,
∴∠BEC=∠AGB,
∴△GAB∽△EBC,
∴,即,
∴AGa,
如图,过点F作FM⊥AB于点M,则∠EMF=90°,
∵点F是BG的中点,HF⊥AD于点H,
∴四边形AHFM是矩形,AHAGa,HFAB=2,
∴AM=HF=2,MF=AHa,
∴ME=2﹣a,
由对称得,EB=EF=a,
在Rt△MEF中,EM2+FM2=EF2,
∴(2﹣a)2+(a)2=a2,
解得:a或a(舍),
故答案为:.
11.【解答】解:连接BD,PC,
S正方形ABCD=1×1=1,
由勾股定理得:,
∵AB=1,
∴,
∴,
∵,
∴,
∵,
当时,m=AA1+CC1+DD1有最小值,
故答案为:.
三、解答题
12.【解答】证明:(1)在平行四边形ABCD中,AO=CO,AD∥BC,
∴∠FAO=∠ECO,
在△AOF和△CEO中,
,
∴△AOF≌△CEO(ASA),
∴AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)∵AF∥CE,
∴∠AFE=∠CEF,
∵EF平分∠AEC,
∴∠AEF=∠CEF,
∴∠AFE=∠AEF,
∴AE=AF,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,
∴AC⊥EF,
∵点E是BC的中点,
∴BE=CE,
∴BE=AF,
∵BE∥AF,
∴四边形ABEF是平行四边形,
∴AB∥EF,
∴AB⊥AC.
13.【解答】(1)解:∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,
∵∠DCE=45°,
∴∠DEC=∠DCE=45°,
∴ED=CD=1,
∴BC=CECD,
∴BD,
∴BD的长是.
(2)证明:如图2,作DP⊥CE于点P,则∠CDE=∠BPC=90°,
∵CF⊥EC,
∴∠FCH=∠BPH=90°,
∵AD∥CB,
∴∠DEC=∠PCB,
∵H为BF的中点,
∴FH=BH,
在△CHF和△PHB中,
,
∴△CHF≌△PHB(AAS),
∴CF=PB,HC=HP,
∴PC=2HC,
∵CF=CD,
∴CD=PB,
在△DEC和△PCB中,
,
∴△DEC≌△PCB(AAS),
∴DE=PC,
∴DE=2HC.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴ED∥FC,
∴∠EDO=∠CFO,
又∵OC=OE,
∵∠EOD=∠COF,
∴△EOD≌△COF(AAS),
∴ED=FC,
∴四边形CDEF是平行四边形,
又∵ED=EF,
∴四边形CDEF是菱形;
(2)解:∵四边形ABCD是平行四边形,四边形CDEF是菱形,
∴AD=BC,ED=FC,FC=FE,
∴AD﹣ED=BC﹣FC,
∴AE=BF=1,
∵ ABCD的周长为22,
∴,
又∵∠ABC=60°,
∴△EFC是等边三角形,
∴CE=EF=5.
15.【解答】(1)证明:∵DE∥AC,DE=OC,
∴四边形OCED是平行四边形.
∵OE=CD,
∴平行四边形OCED是矩形,
∴∠COD=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,CD=AB=BC=4,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴OA=OC=2,
在Rt△OCD中,由勾股定理得:OD2,
由(1)可知,四边形OCED是矩形,
∴CE=OD=2,∠OCE=90°,
∴AE2,
即AE的长为2.
16.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
17.【解答】解:(1)∵四边形ABCD是正方形,四边形AEFG是矩形,
∴AB=BC,AE=GF,∠E=∠F=∠ABC=90°.
又∵∠EBA+∠FBC=∠BCF+∠FBC=90°,
∴∠EBA=∠BCF.
∴△AEB≌△BFC(AAS).
∴AE=BF.
∴GF=BF.
∴∠FBG=∠BGF=45°;
(2)证明:如图1,分别延长AG与BC交于点P.
∵∠PGC=∠BFC=90°,CG=FC,∠PCG=∠BCF,
∴△PCG≌△BCF,
∴PC=BC.
∵AD=BC,
∴AD=PC.
又∵∠ADH=∠PCH=90°,∠AHD=∠PHC,
∴△ADH≌△PCH(AAS).
∴DH=CH.
(3)解:过点C作CM⊥FG于点M,作CN⊥EF于点N,连CG,
则四边形CMFN为矩形,
由(1)可得△AEB≌△BNC,
∴BN=AE=2,CN=BE,
设:CN=BE=x
则:CM=FN=|2﹣3+x|=|x﹣1|,FM=CN=x,
∴GM=|2﹣x|
在Rt△GMC中,
GC2=MC2+MG2=(x﹣1)2+(2﹣x)2=2,
解得:或.
∴或.
18.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠CAD=∠ACD=45°,
∵CP⊥CF,
∴∠FCP=90°=∠BCD,
∴∠BCF=∠DCP,
∵CD=CB,∠CBF=∠CDP=90°,
∴△CDP≌△CBF(ASA),
∴CF=CP;
(2)∵CF平分∠ACB,
∴∠ACF=∠BCF=22.5°,
∴∠BFC=67.5°,
∵△CDP≌△CBF,
∴∠P=∠BFC=67.5°,且∠CAP=45°,
∴∠ACP=∠P=67.5°,
∴AC=AP,
∵ACAB=4,
∴S△ACPAP×CD=8;
(3)在CN上截取NH=FN,连接BH,
∵△CDP≌△CBF,
∴CP=CF,
∵FN=NH,且BN⊥FH,
∴BH=BF,
∴∠BFH=∠BHF=67.5°,
∴∠FBN=∠HBN=∠BCH=22.5°,
∴∠HBC=∠BAM=45°,
∵AB=BC,∠ABM=∠BCH,
∴△AMB≌△BHC(ASA),
∴CH=BM,
∴CF=BM+2FN,
∴CP﹣BM=2FN.
21世纪教育网(www.21cnjy.com)
同课章节目录
