第一章 三角形的证明 章节期中复习(含答案)北师大版2024—2025学年八年级下册
文档属性
| 名称 | 第一章 三角形的证明 章节期中复习(含答案)北师大版2024—2025学年八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 510.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 15:02:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章三角形的证明章节期中复习北师大版2024—2025学年八年级下册
一、选择题
1.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列所给数据中,不能判断△ABC是直角三角形的是( )
A.∠A+∠B=90° B.a:b:c=5:12:13
C.a2+b2=c2 D.∠A:∠B:∠C=3:4:5
2.如图,在△ABC中,已知∠A=30°,∠ABC=70°,D为AC边上一点,且AD=BD.则∠DBC=( )
A.70° B.60° C.50° D.40°
3.如图,在△ABC中,AC的垂直平分线交AB于点D,垂足为点E,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
4.如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
5.如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一条直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,连接FH.给出下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
6.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
7.如图,CE和CF分别是△ABC的内、外角平分线,且EF∥BC交AC于点 P,若AP=2,AC=5,则CE2+CF2的值是 .
8.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= .
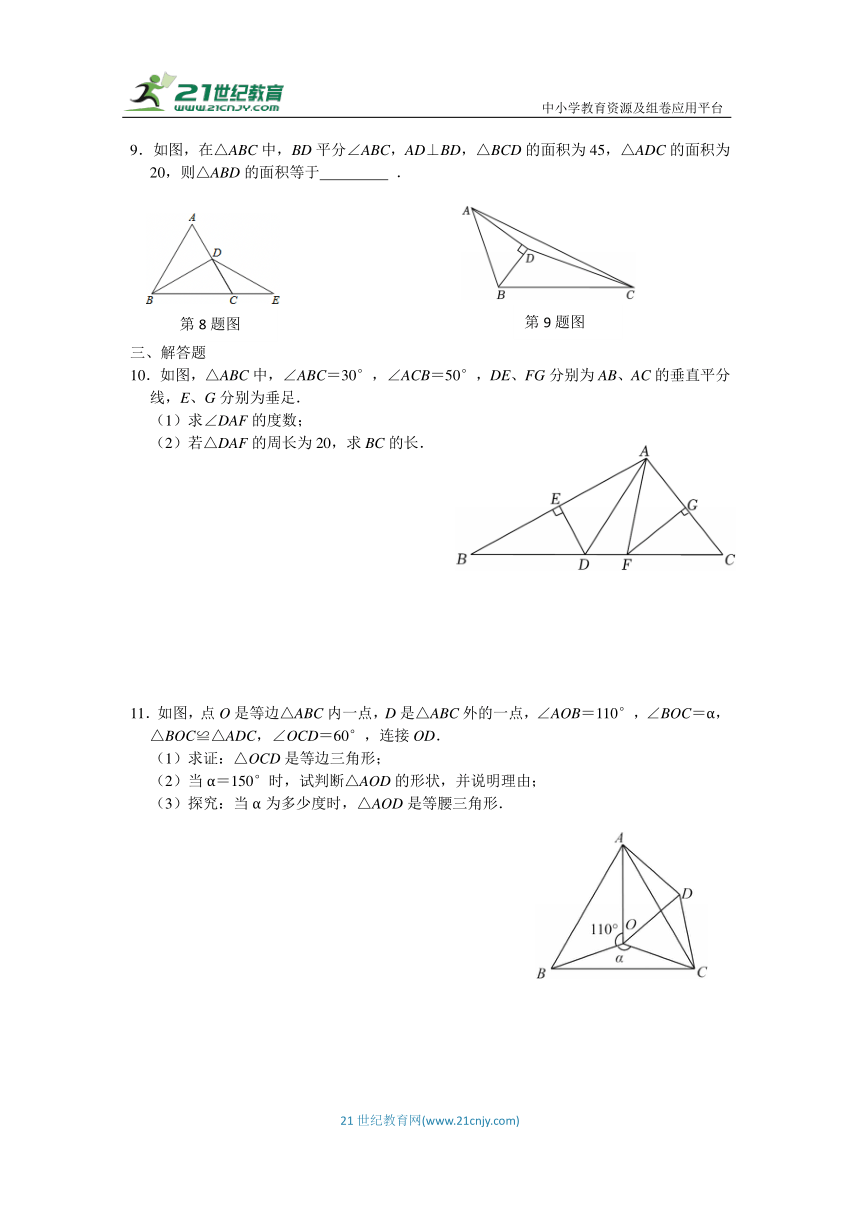
9.如图,在△ABC中,BD平分∠ABC,AD⊥BD,△BCD的面积为45,△ADC的面积为20,则△ABD的面积等于 .
三、解答题
10.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
11.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
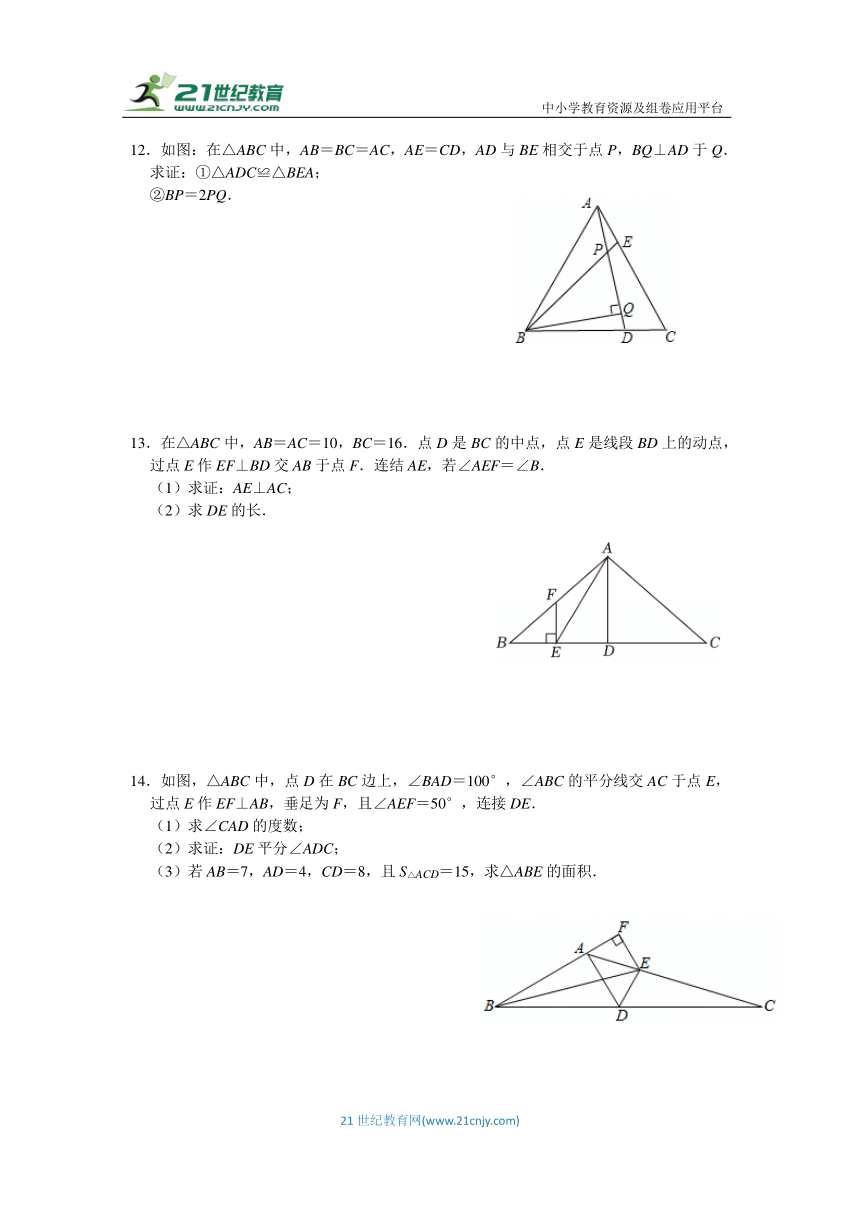
12.如图:在△ABC中,AB=BC=AC,AE=CD,AD与BE相交于点P,BQ⊥AD于Q.
求证:①△ADC≌△BEA;
②BP=2PQ.
13.在△ABC中,AB=AC=10,BC=16.点D是BC的中点,点E是线段BD上的动点,过点E作EF⊥BD交AB于点F.连结AE,若∠AEF=∠B.
(1)求证:AE⊥AC;
(2)求DE的长.
14.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
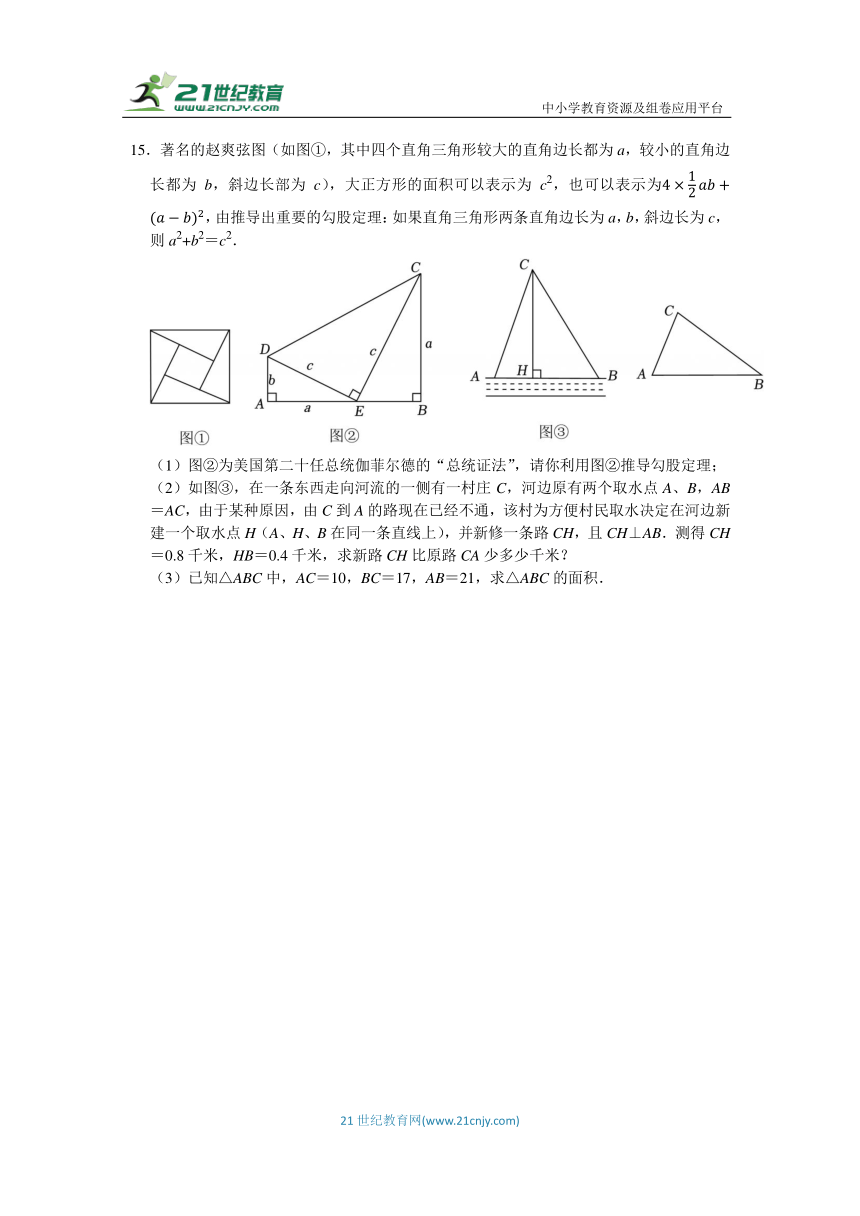
15.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长部为c),大正方形的面积可以表示为c2,也可以表示为,由推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理;
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A、B,AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,且CH⊥AB.测得CH=0.8千米,HB=0.4千米,求新路CH比原路CA少多少千米?
(3)已知△ABC中,AC=10,BC=17,AB=21,求△ABC的面积.
参考答案
一、选择题
1.【解答】解:A、∵∠A+∠B+∠C=180°,∠A+∠B=90°,
∴∠C=180°﹣(∠A+∠B)=90°
∴△ABC是直角三角形,不符合题意;
B、∵a:b:c=5:12:13,
∴设a=5x,b=12x,c=13x,
∴a2+b2=(5x)2+(12x)2=(13x)2=c2,
∴△ABC是直角三角形,不符合题意;
C、∵a2+b2=c2,∴△ABC是直角三角形,不符合题意;
D、∵∠A+∠B+∠C=180°,∠A:∠B:∠C=3:4:5,
∴设∠A=3x,∠B=4x,∠C=5x,
3x+4x+5x=180°,
解得:x=15°,
5x=75°≠90°,
∴△ABC不是直角三角形,符合题意;
故选:D.
2.【解答】解:∵AD=BD,
∴∠A=∠ABD=30°,
∵∠ABC=70°,
∴∠DBC=∠ABC﹣∠ABD=40°,
故选:D.
3.【解答】解:∵DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD
又∵CD平分∠ACB,
∴∠ACB=2∠ACD=100°,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣50°﹣100°=30°,
故选:B.
4.【解答】解:过D点作DE⊥BC于E,如图,
∵BD是∠ABC的平分线,DE⊥BC,DA⊥AB,
∴DE=DA,
∴.
故选:B.
5.【解答】解:∵△ABC和△DCE是等边三角形,
∴∠BCA=∠DCE=60°,AC=BC,CE=CD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),故①正确;
∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠BFC=∠AFG,
∴∠AGB=∠ACB=60°,故②正确;
在△BCF和△ACH中,
,
∴△BCF≌△ACH(ASA),
∴CF=CH,BF=AH;故③正确;
∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形;故④正确.
故选:D.
二、填空题
6.【解答】解:如图,连接BP,
在△ABC中,AB=AC=10,BC=12,AD=8,
∴BD=DC,
∴BP=PC,
∴PC+PQ=BP+PQ=BQ,
∴当B,P,Q共线时,PC+PQ的值最小,
∴当BQ⊥AC时,BQ的值最小,
令AQ'=a,则CQ'=10﹣a,
∵BQ'⊥AC,
∴AB2﹣AQ'2=BC2﹣CQ'2,
即102﹣a2=122﹣(10﹣a)2,
解得a,
∴BQ',
∴PC+PQ的最小值为,
故答案为:.
7.【解答】解:∵CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE∠ACB,∠ACF=∠DCF∠ACD,
∴∠ACE+∠ACF(∠ACB+∠ACD)180°=90°,
∴△CEF是直角三角形,
∵EF∥BC,
∴∠BCE=∠FEC,∠DCF=∠F,
∴∠ACE=∠FEC,∠ACF=∠F,
∴EP=CP,CP=FP,
∴EP=CP=FP,
∵AP=2,AC=5,
∴EP=FP=CP=AC﹣AP=3,
∴EF=EP+FP=6,
在Rt△CEF中,由勾股定理得:CE2+CF2=EF2=62=36,
故答案为:36.
8.【解答】解:∵△ABC为等边三角形,BD为△ABC的高,
∴点D为AC的中点,AC=BC,
∵CE=CD=1,
∴AC=2CD=2,
∴BC=2,
∴BE=BC+CE=2+1=3,
故答案为:3.
9.【解答】解:延长AD交BC于E,如图,
由条件可知∠ABD=∠EBD,∠ADB=∠EDB=90°,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(ASA),
∴AD=ED,
∴S△ABD=S△EBD,S△CDE=S△ACD=20,
∴S△ABD=S△EBD=45﹣20=25.
故答案为:25.
三、解答题
10.【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
11.【解答】证明:(1)∵△BOC≌△ADC,
∴OC=DC,
∵∠OCD=60°,
∴△OCD是等边三角形.
解:
(2)△AOD是直角三角形.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,α=150°,
∴∠ADC=∠BOC=α=150°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形.
(3)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,
α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
12.【解答】证明:(1)∵AB=BC=AC,
∴△ABC是等边三角形.
∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,
∴△ADC≌△BEA.
(2)∵△ADC≌△BEA,
∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.
∴∠BPQ=60°.
∵BQ⊥AD,
∴∠PBQ=30°.
∴BP=2PQ.
13.【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵EF⊥BD,
∴∠AEF+∠AED=90°,
∵∠AEF=∠B,∠B=∠C,
∴∠C+∠AED=90°,
∴∠EAC=90°,
∴AE⊥AC;
(2)解:∵∠EAC=90°,
∴AE2+AC2=CE2,
∵CE=CD+DE=DE+8,
∴AE2=CE2﹣AC2=(DE+8)2﹣102,
∵AB=AC,点D是BC的中点,
∴BD=DC16=8,BC=16,AD⊥BC,
∴AD6,
在Rt△ADE中,AE2=AD2+DE2=62+DE2,
∴(DE+8)2﹣102=62+DE2,
解得:DE=4.5.
14.【解答】(1)解:∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°﹣50°=40°,
∵∠BAD=100°,
∴∠CAD=180°﹣100°﹣40°=40°;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG,
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH,
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC;
(3)解:∵S△ACD=15,
∴AD×EGCD×EH=15,即4×EG8×EG=15,
解得,EG=EH,
∴EF=EH,
∴△ABE的面积AB×EF7.
15.【解答】(1)证明:梯形ABCD的面积为,
也可以表示为,
∴,
即a2+b2=c2;
(2)解:设AC=AB=x千米,
∴AH=AB﹣BH=(x﹣0.6)千米,
∵CA2=CH2+AH2,
∴x2=0.82+(x﹣0.4)2,
∴x=1,
即CA=1千米,
∴CA﹣CH=1﹣0.8=0.2(千米),
答:新路CH比原路CA少0.2千米;
(3)解:作CH⊥AB,垂足为H,
设AH=y,
∴BH=AB﹣AH=21﹣y,
∵CH⊥AB,AB=21,AC=10,BC=17,
∵CH2=CA2﹣AH2,CH2=CB2﹣BH2,
∴CA2﹣AH2=CB2﹣BH2,
即102﹣y2=172﹣(21﹣y)2,
∴y=6,
∴AH=6,
∴.
∴.
21世纪教育网(www.21cnjy.com)
第一章三角形的证明章节期中复习北师大版2024—2025学年八年级下册
一、选择题
1.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列所给数据中,不能判断△ABC是直角三角形的是( )
A.∠A+∠B=90° B.a:b:c=5:12:13
C.a2+b2=c2 D.∠A:∠B:∠C=3:4:5
2.如图,在△ABC中,已知∠A=30°,∠ABC=70°,D为AC边上一点,且AD=BD.则∠DBC=( )
A.70° B.60° C.50° D.40°
3.如图,在△ABC中,AC的垂直平分线交AB于点D,垂足为点E,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
4.如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
5.如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一条直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,连接FH.给出下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
6.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
7.如图,CE和CF分别是△ABC的内、外角平分线,且EF∥BC交AC于点 P,若AP=2,AC=5,则CE2+CF2的值是 .
8.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= .
9.如图,在△ABC中,BD平分∠ABC,AD⊥BD,△BCD的面积为45,△ADC的面积为20,则△ABD的面积等于 .
三、解答题
10.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
11.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
12.如图:在△ABC中,AB=BC=AC,AE=CD,AD与BE相交于点P,BQ⊥AD于Q.
求证:①△ADC≌△BEA;
②BP=2PQ.
13.在△ABC中,AB=AC=10,BC=16.点D是BC的中点,点E是线段BD上的动点,过点E作EF⊥BD交AB于点F.连结AE,若∠AEF=∠B.
(1)求证:AE⊥AC;
(2)求DE的长.
14.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
15.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长部为c),大正方形的面积可以表示为c2,也可以表示为,由推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理;
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A、B,AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,且CH⊥AB.测得CH=0.8千米,HB=0.4千米,求新路CH比原路CA少多少千米?
(3)已知△ABC中,AC=10,BC=17,AB=21,求△ABC的面积.
参考答案
一、选择题
1.【解答】解:A、∵∠A+∠B+∠C=180°,∠A+∠B=90°,
∴∠C=180°﹣(∠A+∠B)=90°
∴△ABC是直角三角形,不符合题意;
B、∵a:b:c=5:12:13,
∴设a=5x,b=12x,c=13x,
∴a2+b2=(5x)2+(12x)2=(13x)2=c2,
∴△ABC是直角三角形,不符合题意;
C、∵a2+b2=c2,∴△ABC是直角三角形,不符合题意;
D、∵∠A+∠B+∠C=180°,∠A:∠B:∠C=3:4:5,
∴设∠A=3x,∠B=4x,∠C=5x,
3x+4x+5x=180°,
解得:x=15°,
5x=75°≠90°,
∴△ABC不是直角三角形,符合题意;
故选:D.
2.【解答】解:∵AD=BD,
∴∠A=∠ABD=30°,
∵∠ABC=70°,
∴∠DBC=∠ABC﹣∠ABD=40°,
故选:D.
3.【解答】解:∵DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD
又∵CD平分∠ACB,
∴∠ACB=2∠ACD=100°,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣50°﹣100°=30°,
故选:B.
4.【解答】解:过D点作DE⊥BC于E,如图,
∵BD是∠ABC的平分线,DE⊥BC,DA⊥AB,
∴DE=DA,
∴.
故选:B.
5.【解答】解:∵△ABC和△DCE是等边三角形,
∴∠BCA=∠DCE=60°,AC=BC,CE=CD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),故①正确;
∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠BFC=∠AFG,
∴∠AGB=∠ACB=60°,故②正确;
在△BCF和△ACH中,
,
∴△BCF≌△ACH(ASA),
∴CF=CH,BF=AH;故③正确;
∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形;故④正确.
故选:D.
二、填空题
6.【解答】解:如图,连接BP,
在△ABC中,AB=AC=10,BC=12,AD=8,
∴BD=DC,
∴BP=PC,
∴PC+PQ=BP+PQ=BQ,
∴当B,P,Q共线时,PC+PQ的值最小,
∴当BQ⊥AC时,BQ的值最小,
令AQ'=a,则CQ'=10﹣a,
∵BQ'⊥AC,
∴AB2﹣AQ'2=BC2﹣CQ'2,
即102﹣a2=122﹣(10﹣a)2,
解得a,
∴BQ',
∴PC+PQ的最小值为,
故答案为:.
7.【解答】解:∵CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE∠ACB,∠ACF=∠DCF∠ACD,
∴∠ACE+∠ACF(∠ACB+∠ACD)180°=90°,
∴△CEF是直角三角形,
∵EF∥BC,
∴∠BCE=∠FEC,∠DCF=∠F,
∴∠ACE=∠FEC,∠ACF=∠F,
∴EP=CP,CP=FP,
∴EP=CP=FP,
∵AP=2,AC=5,
∴EP=FP=CP=AC﹣AP=3,
∴EF=EP+FP=6,
在Rt△CEF中,由勾股定理得:CE2+CF2=EF2=62=36,
故答案为:36.
8.【解答】解:∵△ABC为等边三角形,BD为△ABC的高,
∴点D为AC的中点,AC=BC,
∵CE=CD=1,
∴AC=2CD=2,
∴BC=2,
∴BE=BC+CE=2+1=3,
故答案为:3.
9.【解答】解:延长AD交BC于E,如图,
由条件可知∠ABD=∠EBD,∠ADB=∠EDB=90°,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(ASA),
∴AD=ED,
∴S△ABD=S△EBD,S△CDE=S△ACD=20,
∴S△ABD=S△EBD=45﹣20=25.
故答案为:25.
三、解答题
10.【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
11.【解答】证明:(1)∵△BOC≌△ADC,
∴OC=DC,
∵∠OCD=60°,
∴△OCD是等边三角形.
解:
(2)△AOD是直角三角形.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,α=150°,
∴∠ADC=∠BOC=α=150°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形.
(3)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,
α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
12.【解答】证明:(1)∵AB=BC=AC,
∴△ABC是等边三角形.
∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,
∴△ADC≌△BEA.
(2)∵△ADC≌△BEA,
∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.
∴∠BPQ=60°.
∵BQ⊥AD,
∴∠PBQ=30°.
∴BP=2PQ.
13.【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵EF⊥BD,
∴∠AEF+∠AED=90°,
∵∠AEF=∠B,∠B=∠C,
∴∠C+∠AED=90°,
∴∠EAC=90°,
∴AE⊥AC;
(2)解:∵∠EAC=90°,
∴AE2+AC2=CE2,
∵CE=CD+DE=DE+8,
∴AE2=CE2﹣AC2=(DE+8)2﹣102,
∵AB=AC,点D是BC的中点,
∴BD=DC16=8,BC=16,AD⊥BC,
∴AD6,
在Rt△ADE中,AE2=AD2+DE2=62+DE2,
∴(DE+8)2﹣102=62+DE2,
解得:DE=4.5.
14.【解答】(1)解:∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°﹣50°=40°,
∵∠BAD=100°,
∴∠CAD=180°﹣100°﹣40°=40°;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG,
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH,
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC;
(3)解:∵S△ACD=15,
∴AD×EGCD×EH=15,即4×EG8×EG=15,
解得,EG=EH,
∴EF=EH,
∴△ABE的面积AB×EF7.
15.【解答】(1)证明:梯形ABCD的面积为,
也可以表示为,
∴,
即a2+b2=c2;
(2)解:设AC=AB=x千米,
∴AH=AB﹣BH=(x﹣0.6)千米,
∵CA2=CH2+AH2,
∴x2=0.82+(x﹣0.4)2,
∴x=1,
即CA=1千米,
∴CA﹣CH=1﹣0.8=0.2(千米),
答:新路CH比原路CA少0.2千米;
(3)解:作CH⊥AB,垂足为H,
设AH=y,
∴BH=AB﹣AH=21﹣y,
∵CH⊥AB,AB=21,AC=10,BC=17,
∵CH2=CA2﹣AH2,CH2=CB2﹣BH2,
∴CA2﹣AH2=CB2﹣BH2,
即102﹣y2=172﹣(21﹣y)2,
∴y=6,
∴AH=6,
∴.
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
