第三章 图形的平移与旋转 期中复习(含答案)北师大版2024—2025学年八年级下册
文档属性
| 名称 | 第三章 图形的平移与旋转 期中复习(含答案)北师大版2024—2025学年八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 650.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 14:59:06 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章图形的平移与旋转期中复习北师大版2024—2025学年八年级下册
一、选择题
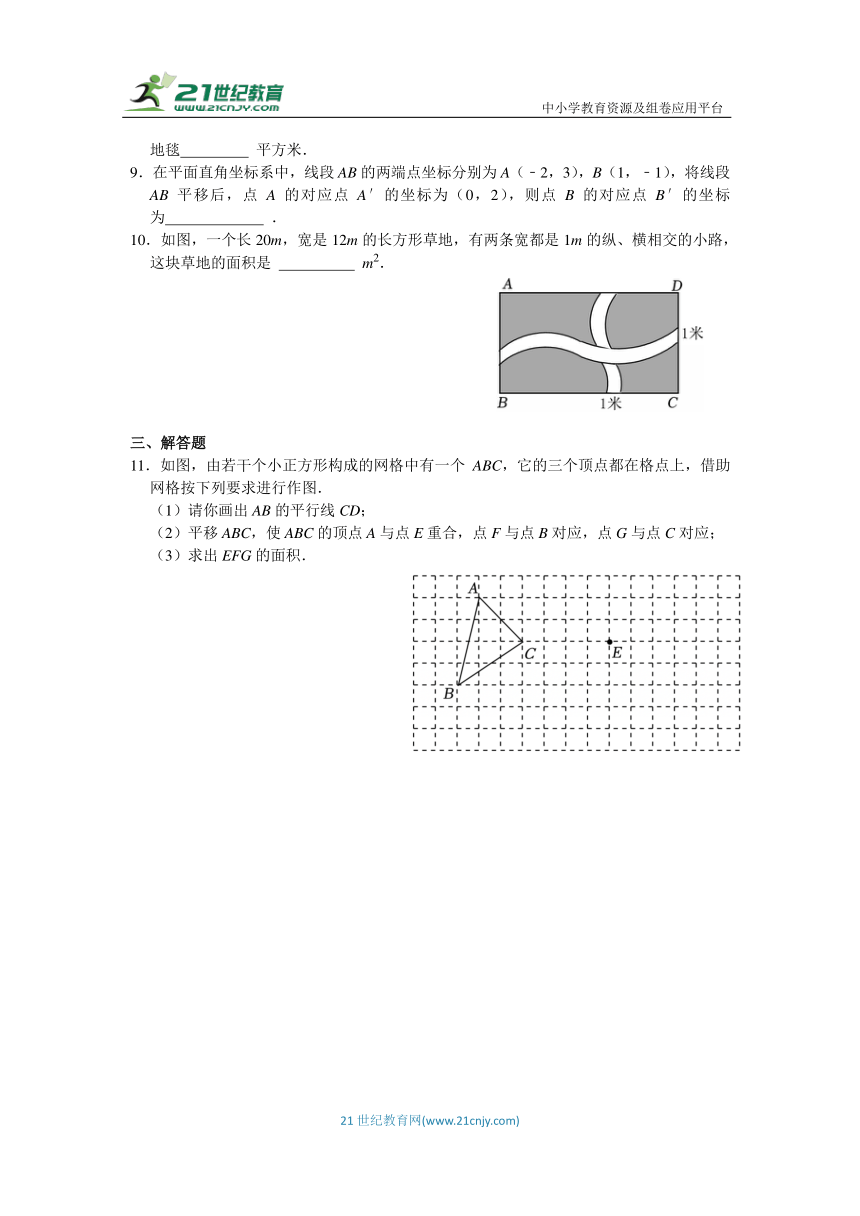
1.下列图形是中心对称图形的是( )
A. B. C. D.
2.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
3.如图,将△ABC绕着点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,点C,D,E恰好在一条直线上.若CD=2,BC=1,则AC的长为( )
A. B. C. D.
4.如图,把△ABC绕点C顺时针旋转35°得到△A′B′C,点A、B的对应点分别为点A′、B′,A′B′交AC边于点D.若∠A′DC=95°,则∠A的度数为( )
A.40° B.45° C.50° D.55°
5.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=( )
A.2 B.3 C.4 D.5
二、填空题
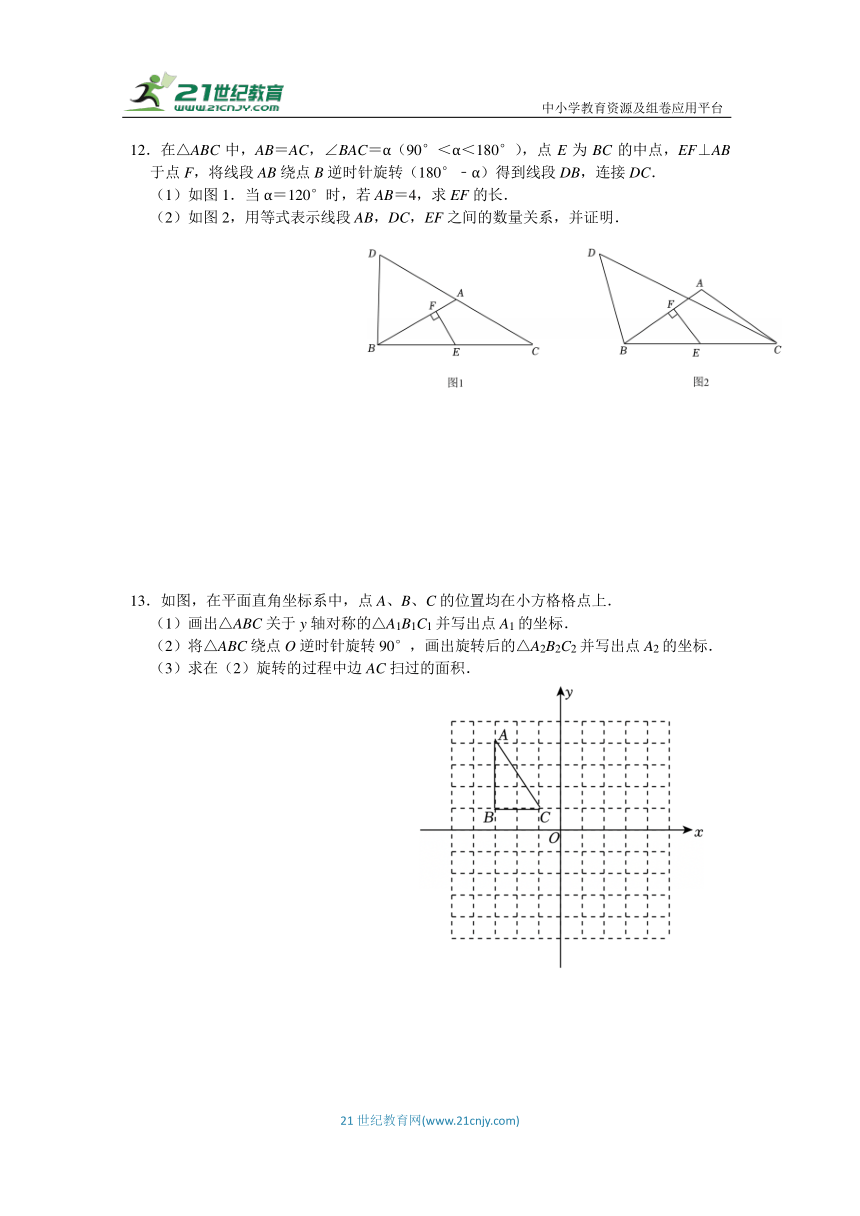
6.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转α得到的,点A′与点A对应,则α的大小为 .
7.在△ABC中,∠C=90°,∠A=25°,点O是AB的中点,将OB绕点O向三角形外部旋转α角时(0°<α<180°),得到OP,当△ACP恰为轴对称图形时,α的值为 .
8.如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,那么至少要买地毯 平方米.
9.在平面直角坐标系中,线段AB的两端点坐标分别为A(﹣2,3),B(1,﹣1),将线段AB平移后,点A的对应点A′的坐标为(0,2),则点B的对应点B′的坐标为 .
10.如图,一个长20m,宽是12m的长方形草地,有两条宽都是1m的纵、横相交的小路,这块草地的面积是 m2.
三、解答题
11.如图,由若干个小正方形构成的网格中有一个ABC,它的三个顶点都在格点上,借助网格按下列要求进行作图.
(1)请你画出AB的平行线CD;
(2)平移ABC,使ABC的顶点A与点E重合,点F与点B对应,点G与点C对应;
(3)求出EFG的面积.
12.在△ABC中,AB=AC,∠BAC=α(90°<α<180°),点E为BC的中点,EF⊥AB于点F,将线段AB绕点B逆时针旋转(180°﹣α)得到线段DB,连接DC.
(1)如图1.当α=120°时,若AB=4,求EF的长.
(2)如图2,用等式表示线段AB,DC,EF之间的数量关系,并证明.
13.如图,在平面直角坐标系中,点A、B、C的位置均在小方格格点上.
(1)画出△ABC关于y轴对称的△A1B1C1并写出点A1的坐标.
(2)将△ABC绕点O逆时针旋转90°,画出旋转后的△A2B2C2并写出点A2的坐标.
(3)求在(2)旋转的过程中边AC扫过的面积.
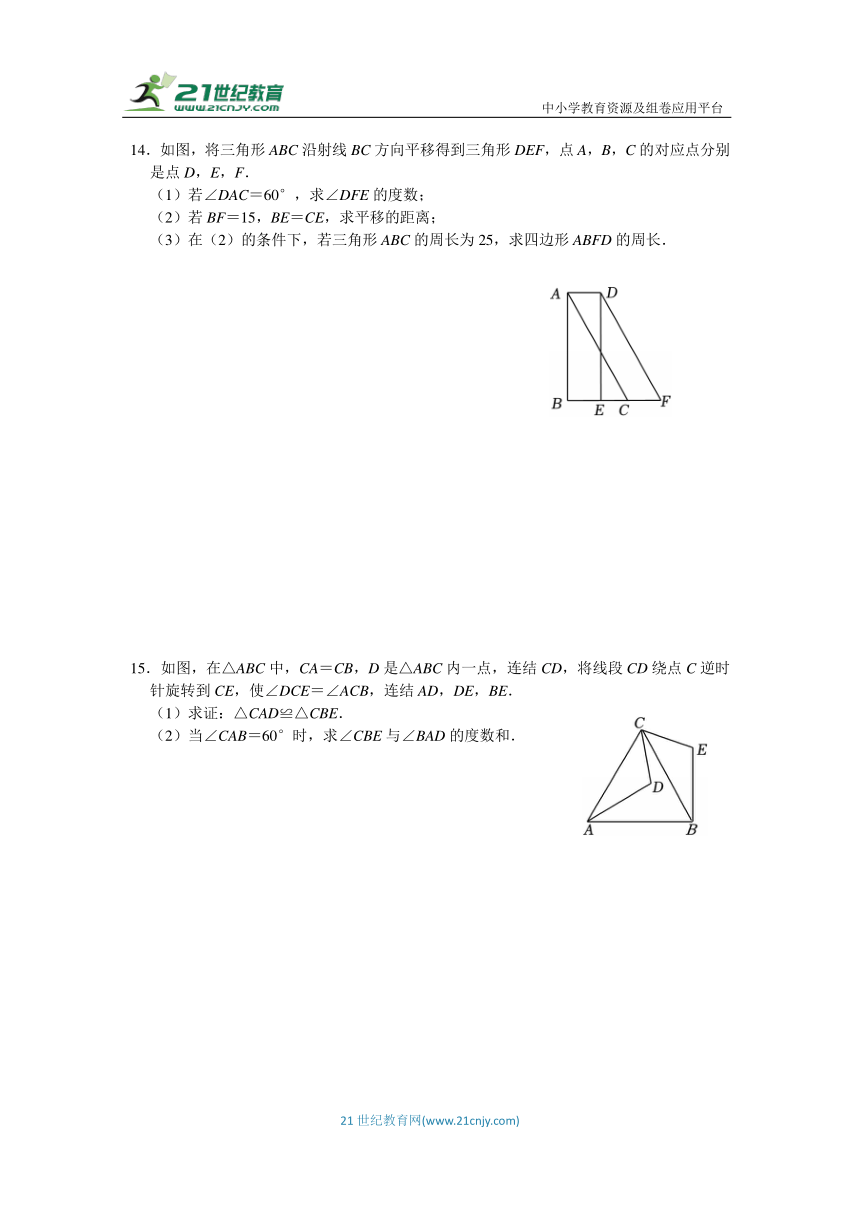
14.如图,将三角形ABC沿射线BC方向平移得到三角形DEF,点A,B,C的对应点分别是点D,E,F.
(1)若∠DAC=60°,求∠DFE的度数;
(2)若BF=15,BE=CE,求平移的距离;
(3)在(2)的条件下,若三角形ABC的周长为25,求四边形ABFD的周长.
15.如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
参考答案
一、选择题
1.【解答】解:选项B中的图形能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以是中心对称图形.
故选:B.
2.【解答】解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DF=AC,AD=CF=3cm,
∵△ABC的周长为20cm,即AB+BC+AC=20cm,
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26(cm),
即四边形ABFD的周长为26cm.
故选:D.
3.【解答】解:∵将△ABC绕着点A顺时针旋转90°得到△ADE,
∴DE=BC=1,∠CAE=90°,AC=AE,
∴△ACE是等腰直角三角形,CE=CD+DE=2+1=3,
∴ACCE.
故选:C.
4.【解答】解:∵△ABC绕点C顺时针旋转35°得到△A′B′C,
∴∠A=∠A',∠A'CA=35°,
∴∠A'=180°﹣∠A′DC﹣∠A'CD=180°﹣95°﹣35°=50°,
∴∠A=50°.
故选:C.
5.【解答】解:∵△ABC绕点A顺时针旋转 60°得到△AED,
∴AB=AE,∠BAE=60°,
∴△AEB是等边三角形,
∴BE=AB,
∵AB=3,
∴BE=3.
故选:B.
二、填空题
6.【解答】解:如图:连接AA′,BB′,作线段AA′,BB′的垂直平分线交点为O,点O即为旋转中心.连接OA,OB′
∠AOA′即为旋转角,
∴旋转角为90°
故答案为:90°
7.【解答】解:在Rt△ACB中,
∵∠ACB=90°,AO=OB,
∴OC=OA=OB,
∴∠OAC=∠ACO=25°,∠COB=50°,∠AOC=130°.
①如图1中,
当AC=AP时,
在△AOC和△AOP中,
,
∴△AOC≌△AOP(SSS),
∴∠AOC=∠AOP=130°,
∴α=∠POB=50°.
②如图2中,当PC=PA时,同理可证△OPA≌△OPC,
∴∠POA=∠POC(360°﹣∠AOC)=115°,
∴α=∠POB=∠POC﹣∠COB=65°.
③如图3中,当CA=CP时,同理可证△COA≌△COB,
∴∠COP=∠AOC=130°,
∴α=∠POB=∠POC﹣∠COB=80°
故答案为:50°或65°或80°.
8.【解答】解:地毯的长度为:3+5=8(米),
∵台阶宽为2米,
∴8×2=16(平方米).
∴至少要买地毯16平方米.
故答案为:16.
9.【解答】解:∵线段AB的两端点坐标分别为A(﹣2,3),B(1,﹣1),将线段AB平移后,点A的对应点A′的坐标为(0,2),
∴0﹣(﹣2)=2,2﹣3=﹣1,
∴线段AB向右平移2个单位,再向下平移1个单位即可得到线段A′B′,
∴点B的对应点B′的坐标为(1+2,﹣1﹣1),即(3,﹣2).
故答案为:(3,﹣2).
10.【解答】解:由图可得,这块草地的绿地面积为(20﹣1)×(12﹣1)=209(m2).
故答案为:209.
三、解答题
11.【解答】解:(1)AB的平行线CD,如图1即为所求;
(2)平移ABC后得到的△EFG,如图2即为所求;
(3).
12.【解答】解:(1)如图1,连接AE,
∵AB=AC,点E为BC的中点,
∴AE⊥BC,
∴∠AEB=90°,
∵∠BAC=α=120°,AB=4,
∴∠ABC=∠C(180°﹣∠BAC)=30°,
∴AEAB=2,
∵EF⊥AB于点F,
∴∠AFE=90°,
∴∠AEF=90°﹣∠BAE=∠ABC=30°,
∴AFAE=1,
∴EF,
∴EF的长是.
(2)AB2+16EF2=CD2,
证明:如图2,连接AE、AD,取AC的中点Q,作BL⊥AD于点L,连接EQ、LQ、LF,
∵将线段AB绕点B逆时针旋转(180°﹣α)得到线段DB,
∴AD=AB,∠ABD=180°﹣α,
∴AL=DL,∠ABL=∠DBL(180°﹣α)=90°α,
∵AB=AC,点E为BC的中点,
∴AE⊥BC,∠BAE=∠CAE∠BACα,
∴∠ALB=∠AEB=90°,
∴∠ABE=90°﹣∠BAE=90°α,
∴∠ABL=∠ABE,
在△ABL和△ABE中,
,
∴△ABL≌△ABE(AAS),
∴BL=BE,
在△LBF和△EBF中,
,
∴△LBF≌△EBF(SAS),
∴LF=EF,∠BFL=∠BFE=90°,
∴∠BFL+∠BFE=180°,
∴E、F、L三点在同一条直线上,
∴EL=2EF,
∵E、Q、L分别是BC、AC、AD的中点,
∴QE∥AB,QEAB,QLCD,
∴∠LEQ=∠BFE=90°,
∴QE2+EL2=QL2,
∴(AB)2+(2EF)2=(CD)2,
∴AB2+16EF2=CD2.
13.【解答】解:(1)如图,△A1B1C1即为所求.
由图可得,点A1的坐标为(3,4).
(2)如图,△A2B2C2即为所求.
由图可得,点A2的坐标为(﹣4,﹣3).
(3)由勾股定理得,OA5,OC,
∴旋转的过程中边AC扫过的面积为.
14.【解答】解:(1)∵△ABC沿射线BC方向平移得到△DEF,
∴AC∥DF,AD∥BF,
∴∠ACB=∠DFE,∠ACB=∠DAC,
∴∠DFE=∠DAC=60°;
(2)由平移的性质可得BE=CF,
又∵BE=CE,
∴,
∴平移的距离为5;
(3)由平移的性质可得AD=BE=CF=5,DF=AC,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=25+2×5=35.
15.【解答】(1)证明:由旋转得,CD=CE.
∵∠DCE=∠ACB,
∴∠DCE﹣∠DCB=∠ACB﹣∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠CBA=60°,CA=CB,
∴△ABC是等边三角形,
∴∠CAB=60°.
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
21世纪教育网(www.21cnjy.com)
第三章图形的平移与旋转期中复习北师大版2024—2025学年八年级下册
一、选择题
1.下列图形是中心对称图形的是( )
A. B. C. D.
2.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
3.如图,将△ABC绕着点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,点C,D,E恰好在一条直线上.若CD=2,BC=1,则AC的长为( )
A. B. C. D.
4.如图,把△ABC绕点C顺时针旋转35°得到△A′B′C,点A、B的对应点分别为点A′、B′,A′B′交AC边于点D.若∠A′DC=95°,则∠A的度数为( )
A.40° B.45° C.50° D.55°
5.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=( )
A.2 B.3 C.4 D.5
二、填空题
6.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转α得到的,点A′与点A对应,则α的大小为 .
7.在△ABC中,∠C=90°,∠A=25°,点O是AB的中点,将OB绕点O向三角形外部旋转α角时(0°<α<180°),得到OP,当△ACP恰为轴对称图形时,α的值为 .
8.如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,那么至少要买地毯 平方米.
9.在平面直角坐标系中,线段AB的两端点坐标分别为A(﹣2,3),B(1,﹣1),将线段AB平移后,点A的对应点A′的坐标为(0,2),则点B的对应点B′的坐标为 .
10.如图,一个长20m,宽是12m的长方形草地,有两条宽都是1m的纵、横相交的小路,这块草地的面积是 m2.
三、解答题
11.如图,由若干个小正方形构成的网格中有一个ABC,它的三个顶点都在格点上,借助网格按下列要求进行作图.
(1)请你画出AB的平行线CD;
(2)平移ABC,使ABC的顶点A与点E重合,点F与点B对应,点G与点C对应;
(3)求出EFG的面积.
12.在△ABC中,AB=AC,∠BAC=α(90°<α<180°),点E为BC的中点,EF⊥AB于点F,将线段AB绕点B逆时针旋转(180°﹣α)得到线段DB,连接DC.
(1)如图1.当α=120°时,若AB=4,求EF的长.
(2)如图2,用等式表示线段AB,DC,EF之间的数量关系,并证明.
13.如图,在平面直角坐标系中,点A、B、C的位置均在小方格格点上.
(1)画出△ABC关于y轴对称的△A1B1C1并写出点A1的坐标.
(2)将△ABC绕点O逆时针旋转90°,画出旋转后的△A2B2C2并写出点A2的坐标.
(3)求在(2)旋转的过程中边AC扫过的面积.
14.如图,将三角形ABC沿射线BC方向平移得到三角形DEF,点A,B,C的对应点分别是点D,E,F.
(1)若∠DAC=60°,求∠DFE的度数;
(2)若BF=15,BE=CE,求平移的距离;
(3)在(2)的条件下,若三角形ABC的周长为25,求四边形ABFD的周长.
15.如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
参考答案
一、选择题
1.【解答】解:选项B中的图形能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以是中心对称图形.
故选:B.
2.【解答】解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DF=AC,AD=CF=3cm,
∵△ABC的周长为20cm,即AB+BC+AC=20cm,
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26(cm),
即四边形ABFD的周长为26cm.
故选:D.
3.【解答】解:∵将△ABC绕着点A顺时针旋转90°得到△ADE,
∴DE=BC=1,∠CAE=90°,AC=AE,
∴△ACE是等腰直角三角形,CE=CD+DE=2+1=3,
∴ACCE.
故选:C.
4.【解答】解:∵△ABC绕点C顺时针旋转35°得到△A′B′C,
∴∠A=∠A',∠A'CA=35°,
∴∠A'=180°﹣∠A′DC﹣∠A'CD=180°﹣95°﹣35°=50°,
∴∠A=50°.
故选:C.
5.【解答】解:∵△ABC绕点A顺时针旋转 60°得到△AED,
∴AB=AE,∠BAE=60°,
∴△AEB是等边三角形,
∴BE=AB,
∵AB=3,
∴BE=3.
故选:B.
二、填空题
6.【解答】解:如图:连接AA′,BB′,作线段AA′,BB′的垂直平分线交点为O,点O即为旋转中心.连接OA,OB′
∠AOA′即为旋转角,
∴旋转角为90°
故答案为:90°
7.【解答】解:在Rt△ACB中,
∵∠ACB=90°,AO=OB,
∴OC=OA=OB,
∴∠OAC=∠ACO=25°,∠COB=50°,∠AOC=130°.
①如图1中,
当AC=AP时,
在△AOC和△AOP中,
,
∴△AOC≌△AOP(SSS),
∴∠AOC=∠AOP=130°,
∴α=∠POB=50°.
②如图2中,当PC=PA时,同理可证△OPA≌△OPC,
∴∠POA=∠POC(360°﹣∠AOC)=115°,
∴α=∠POB=∠POC﹣∠COB=65°.
③如图3中,当CA=CP时,同理可证△COA≌△COB,
∴∠COP=∠AOC=130°,
∴α=∠POB=∠POC﹣∠COB=80°
故答案为:50°或65°或80°.
8.【解答】解:地毯的长度为:3+5=8(米),
∵台阶宽为2米,
∴8×2=16(平方米).
∴至少要买地毯16平方米.
故答案为:16.
9.【解答】解:∵线段AB的两端点坐标分别为A(﹣2,3),B(1,﹣1),将线段AB平移后,点A的对应点A′的坐标为(0,2),
∴0﹣(﹣2)=2,2﹣3=﹣1,
∴线段AB向右平移2个单位,再向下平移1个单位即可得到线段A′B′,
∴点B的对应点B′的坐标为(1+2,﹣1﹣1),即(3,﹣2).
故答案为:(3,﹣2).
10.【解答】解:由图可得,这块草地的绿地面积为(20﹣1)×(12﹣1)=209(m2).
故答案为:209.
三、解答题
11.【解答】解:(1)AB的平行线CD,如图1即为所求;
(2)平移ABC后得到的△EFG,如图2即为所求;
(3).
12.【解答】解:(1)如图1,连接AE,
∵AB=AC,点E为BC的中点,
∴AE⊥BC,
∴∠AEB=90°,
∵∠BAC=α=120°,AB=4,
∴∠ABC=∠C(180°﹣∠BAC)=30°,
∴AEAB=2,
∵EF⊥AB于点F,
∴∠AFE=90°,
∴∠AEF=90°﹣∠BAE=∠ABC=30°,
∴AFAE=1,
∴EF,
∴EF的长是.
(2)AB2+16EF2=CD2,
证明:如图2,连接AE、AD,取AC的中点Q,作BL⊥AD于点L,连接EQ、LQ、LF,
∵将线段AB绕点B逆时针旋转(180°﹣α)得到线段DB,
∴AD=AB,∠ABD=180°﹣α,
∴AL=DL,∠ABL=∠DBL(180°﹣α)=90°α,
∵AB=AC,点E为BC的中点,
∴AE⊥BC,∠BAE=∠CAE∠BACα,
∴∠ALB=∠AEB=90°,
∴∠ABE=90°﹣∠BAE=90°α,
∴∠ABL=∠ABE,
在△ABL和△ABE中,
,
∴△ABL≌△ABE(AAS),
∴BL=BE,
在△LBF和△EBF中,
,
∴△LBF≌△EBF(SAS),
∴LF=EF,∠BFL=∠BFE=90°,
∴∠BFL+∠BFE=180°,
∴E、F、L三点在同一条直线上,
∴EL=2EF,
∵E、Q、L分别是BC、AC、AD的中点,
∴QE∥AB,QEAB,QLCD,
∴∠LEQ=∠BFE=90°,
∴QE2+EL2=QL2,
∴(AB)2+(2EF)2=(CD)2,
∴AB2+16EF2=CD2.
13.【解答】解:(1)如图,△A1B1C1即为所求.
由图可得,点A1的坐标为(3,4).
(2)如图,△A2B2C2即为所求.
由图可得,点A2的坐标为(﹣4,﹣3).
(3)由勾股定理得,OA5,OC,
∴旋转的过程中边AC扫过的面积为.
14.【解答】解:(1)∵△ABC沿射线BC方向平移得到△DEF,
∴AC∥DF,AD∥BF,
∴∠ACB=∠DFE,∠ACB=∠DAC,
∴∠DFE=∠DAC=60°;
(2)由平移的性质可得BE=CF,
又∵BE=CE,
∴,
∴平移的距离为5;
(3)由平移的性质可得AD=BE=CF=5,DF=AC,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=25+2×5=35.
15.【解答】(1)证明:由旋转得,CD=CE.
∵∠DCE=∠ACB,
∴∠DCE﹣∠DCB=∠ACB﹣∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠CBA=60°,CA=CB,
∴△ABC是等边三角形,
∴∠CAB=60°.
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
21世纪教育网(www.21cnjy.com)
同课章节目录
