2.3一元二次方程的应用之图形面积问题期中专题复习(含解析)
文档属性
| 名称 | 2.3一元二次方程的应用之图形面积问题期中专题复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 153.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 07:49:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.3一元二次方程的应用之图形面积问题期中专题复习
浙教版2024—2025学年八年级下册
一、选择题
1.扬帆中学有一块长30m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为( )
A.(30﹣x)(20﹣x)=×20×30
B.(30﹣2x)(20﹣x)=×20×30
C.30x+2×20x=×20×30
D.(30﹣2x)(20﹣x)=×20×30
二、填空题
2.如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m2,设道路的宽为xm,则根据题意,可列方程为 .
三、解答题
3.如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.
4.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
5.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
6.如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
7.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
8.某初中学校要新建一块篮球场地(如图所示),要求:①篮球场地的长和宽分别为28米和16米;②在篮球场地四周修建宽度相等的安全区域;③篮球场地及安全区域的总面积为640m2.
(1)求安全区域的宽度.
(2)某公司希望用50万元承包这项工程,该单位认为金额太高需要降价,通过两次协商,最终以32万元达成一致.若两次降价的百分率相同,求每次降价的百分率.
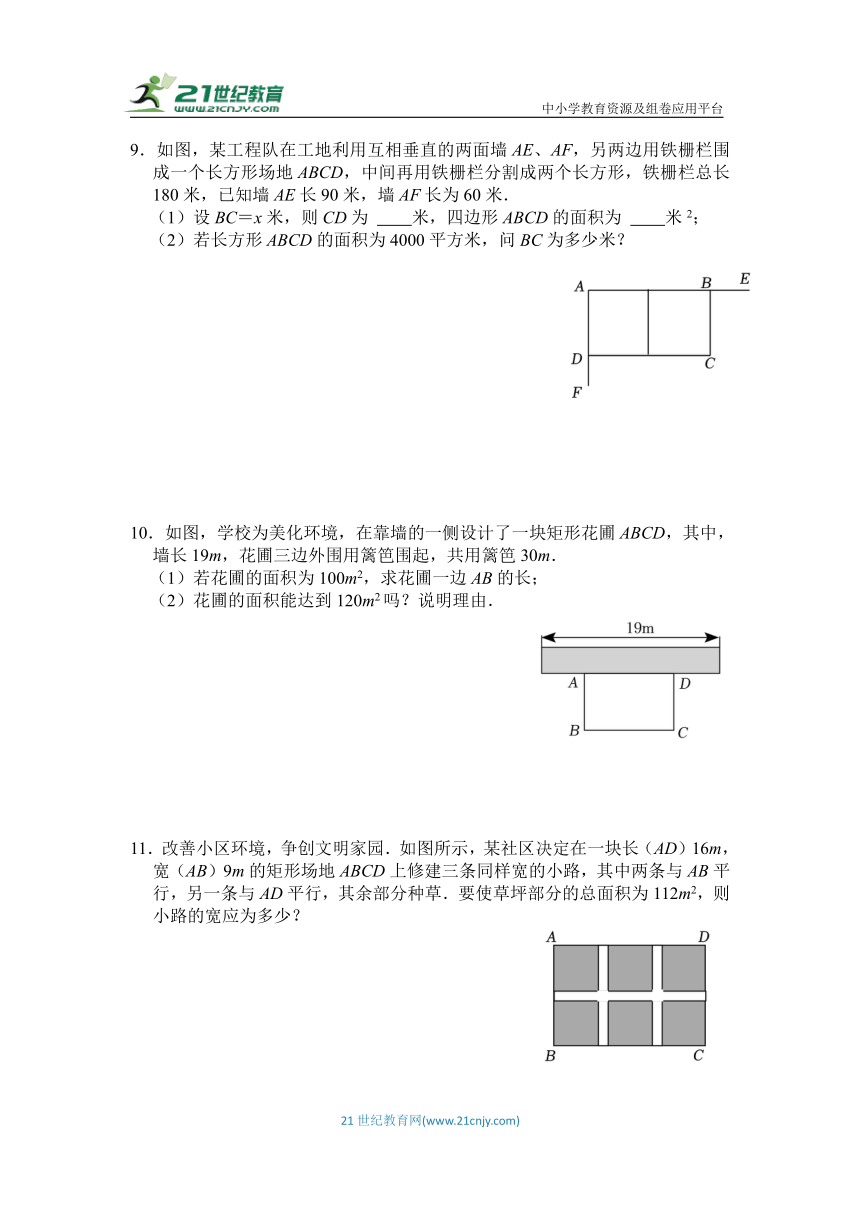
9.如图,某工程队在工地利用互相垂直的两面墙AE、AF,另两边用铁栅栏围成一个长方形场地ABCD,中间再用铁栅栏分割成两个长方形,铁栅栏总长180米,已知墙AE长90米,墙AF长为60米.
(1)设BC=x米,则CD为 米,四边形ABCD的面积为 米2;
(2)若长方形ABCD的面积为4000平方米,问BC为多少米?
10.如图,学校为美化环境,在靠墙的一侧设计了一块矩形花圃ABCD,其中,墙长19m,花圃三边外围用篱笆围起,共用篱笆30m.
(1)若花圃的面积为100m2,求花圃一边AB的长;
(2)花圃的面积能达到120m2吗?说明理由.
11.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
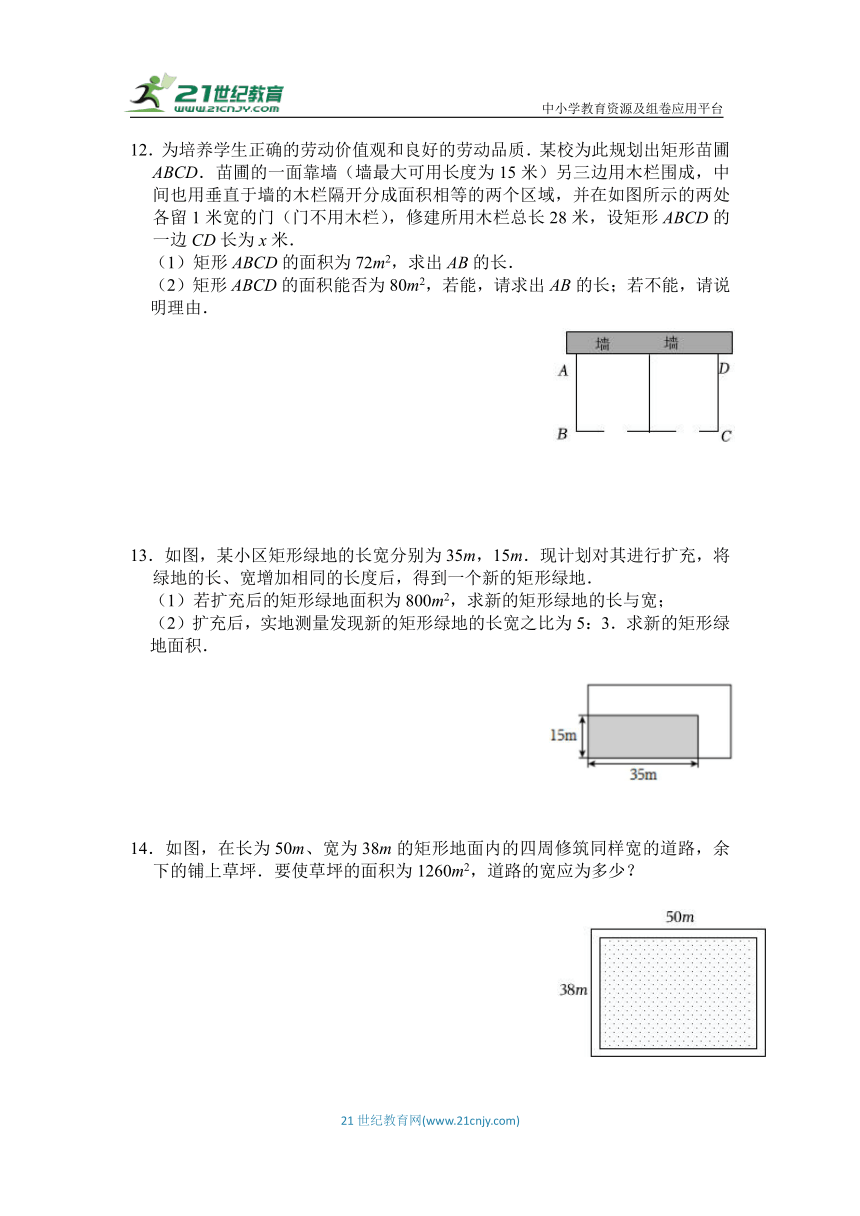
12.为培养学生正确的劳动价值观和良好的劳动品质.某校为此规划出矩形苗圃ABCD.苗圃的一面靠墙(墙最大可用长度为15米)另三边用木栏围成,中间也用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留1米宽的门(门不用木栏),修建所用木栏总长28米,设矩形ABCD的一边CD长为x米.
(1)矩形ABCD的面积为72m2,求出AB的长.
(2)矩形ABCD的面积能否为80m2,若能,请求出AB的长;若不能,请说明理由.
13.如图,某小区矩形绿地的长宽分别为35m,15m.现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地.
(1)若扩充后的矩形绿地面积为800m2,求新的矩形绿地的长与宽;
(2)扩充后,实地测量发现新的矩形绿地的长宽之比为5:3.求新的矩形绿地面积.
14.如图,在长为50m、宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260m2,道路的宽应为多少?
15.为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图),生态园一面靠墙(墙足够长),另外三面用18m的篱笆围成.生态园的面积能否为40m2?如果能,请求出AB的长;如果不能,请说明理由.
16.如图,老李想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个2m宽的门(建在EF处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为640m2的羊圈?
(2)羊圈的面积能达到650m2吗?如果能,请你给出设计方案;如果不能,请说明理由.
17.如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s,2cm/s的速度从点A,C同时出发,沿规定路线移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,问经过多长时间P,Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
参考答案
一、选择题
1.【解答】解:设花带的宽度为xm,则可列方程为(30﹣2x)(20﹣x)=×20×30,
故选:D.
二、填空题
2.【解答】解:∵道路的宽应为x米,
∴由题意得,(12﹣x)(8﹣x)=77,
故答案为:(12﹣x)(8﹣x)=77.
三、解答题
3.【解答】解:设小路的宽为xm,依题意有
(40﹣x)(32﹣x)=1140,
整理,得x2﹣72x+140=0.
解得x1=2,x2=70(不合题意,舍去).
答:小路的宽应是2m.
4.【解答】解:设AB的长度为x米,则BC的长度为(100﹣4x)米.
根据题意得 (100﹣4x)x=400,
解得 x1=20,x2=5.
则100﹣4x=20或100﹣4x=80.
∵80>25,
∴x2=5舍去.
即AB=20,BC=20.
答:羊圈的边长AB,BC分别是20米、20米.
5.【解答】解:设小路的宽应为xm,
根据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
6.【解答】解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
7.【解答】解:设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
8.【解答】解:(1)设安全区域的宽度为x米,由题意得,(28+2x)(16+2x)=640
整理得x2+22x﹣48=0,
解得x1=2,x2=﹣24(不符合题意,舍去),
答:安全区域的宽度为2米;
(2)设每次降价的百分率为a,由题意得,
50(1﹣a)2=32,
解得a1=1.8(舍去),a2=0.2=20%,
答:每次降价的百分率为20%.
9.【解答】解:(1)设BC=x米,则CD=(180﹣2x)米.四边形ABCD的面积为x(180﹣2x)米2,
故答案为:(180﹣2x),x(180﹣2x);
(2)由题意,得:x(180﹣2x)=4000,
整理,得:x2﹣90x+2000=0,
解得:x=40或x=50,
当x=40时,180﹣2x=100>90,不符合题意,舍去;
当x=50时,180﹣2x=80<90,符合题意;
答:BC=50米,长方形的面积为4000平方米.
10.【解答】解:(1)设AB的长为x米,
由题意可得:x(30﹣2x)=100,
解得:x1=5,x2=10,
∵30﹣2x≤19,
∴x=10,
答:AB的长为10米;
(2)花圃的面积不能达到120m2.理由如下:
设AB的长为y米,
由题意可得:y(30﹣2y)=120,
∴Δ=225﹣240=﹣15<0,
∴方程无解,
∴花圃的面积不能达到120m2.
11.【解答】解:设小路的宽应为x m,
根据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
12.【解答】解:(1)设AB=x m,则BC=(28+2﹣3x)m,
根据题意得:x(28+2﹣3x)=72,
整理得:x2﹣10x+24=0,
解得:x1=4,x2=6,
当x=4时,28+2﹣3x=28+2﹣3×4=18>15,不符合题意,舍去;
当x=6时,28+2﹣3x=28+2﹣3×6=12<15,符合题意.
答:AB的长为6m;
(2)矩形ABCD的面积不能为80m2,理由如下:
假设矩形ABCD的面积能为80m2,设AB=y m,则BC=(28+2﹣3y)m,
根据题意得:y(28+2﹣3y)=80,
整理得:3y2﹣30y+80=0,
∵Δ=(﹣30)2﹣4×3×80=﹣60<0,
∴原方程没有实数根,
∴假设不成立,即矩形ABCD的面积不能为80m2.
13.【解答】解:(1)设将绿地的长、宽增加x m,则新的矩形绿地的长为(35+x)m,宽为(15+x)m,
根据题意得:(35+x)(15+x)=800,
整理得:x2+50x﹣275=0
解得:x1=5,x2=﹣55(不符合题意,舍去),
∴35+x=35+5=40,15+x=15+5=20.
答:新的矩形绿地的长为40m,宽为20m.
(2)设将绿地的长、宽增加y m,则新的矩形绿地的长为(35+y)m,宽为(15+y)m,
根据题意得:(35+y):(15+y)=5:3,
即3(35+y)=5(15+y),
解得:y=15,
∴(35+y)(15+y)=(35+15)×(15+15)=1500.
答:新的矩形绿地面积为1500m2.
14.【解答】解:设路宽应为x米
根据等量关系列方程得:(50﹣2x)(38﹣2x)=1260,
解得:x=4或40,
40不合题意,舍去,
所以x=4,
答:道路的宽应为4米.
15.【解答】解:生态园的面积能为40m2,理由如下:
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
设AB的长度为x m,则BC的长度为m,
由题意得:x =40,
整理得:x2﹣18x+80=0,
解得:x1=10,x2=8,
∴生态园的面积能为40m2,AB的长为10m或8m.
16.【解答】解:(1)设矩形ABCD的边AB=x m,则边BC=70﹣2x+2=(72﹣2x)m.
根据题意,得x(72﹣2x)=640,
化简,得 x2﹣36x+320=0,
解得 x1=16,x2=20,
当x=16时,72﹣2x=72﹣32=40(m),
当x=20时,72﹣2x=72﹣40=32(m).
答:当羊圈的长为40m,宽为16m或长为32m,宽为20m时,能围成一个面积为640m2 的羊圈;
(2)答:不能,
理由:由题意,得x(72﹣2x)=650,
化简,得 x2﹣36x+325=0,
Δ=(﹣36)2﹣4×325=﹣4<0,
∴一元二次方程没有实数根.
∴羊圈的面积不能达到 650m2.
17.【解答】解:(1)过点P作PE⊥CD于E,
设x秒后,点P和点Q的距离是10cm.(16﹣2x﹣3x)2+62=102,
∴,;
∴经过或,P、Q两点之间的距离是10cm;
(2)连接BQ.设经过ys后△PBQ的面积为12cm2.
①当时,PB=16﹣3y,
∴,即,
解得y=4;
②当<y≤时,BP=3y﹣16,QC=2y,
则,
解得(舍去);
③时,QP=CQ﹣PC=22﹣y,
则,
解得y=18(舍去).
综上所述,经过4秒或6秒,△PBQ的面积为12cm2.
21世纪教育网(www.21cnjy.com)
2.3一元二次方程的应用之图形面积问题期中专题复习
浙教版2024—2025学年八年级下册
一、选择题
1.扬帆中学有一块长30m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为( )
A.(30﹣x)(20﹣x)=×20×30
B.(30﹣2x)(20﹣x)=×20×30
C.30x+2×20x=×20×30
D.(30﹣2x)(20﹣x)=×20×30
二、填空题
2.如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m2,设道路的宽为xm,则根据题意,可列方程为 .
三、解答题
3.如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.
4.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
5.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
6.如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
7.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
8.某初中学校要新建一块篮球场地(如图所示),要求:①篮球场地的长和宽分别为28米和16米;②在篮球场地四周修建宽度相等的安全区域;③篮球场地及安全区域的总面积为640m2.
(1)求安全区域的宽度.
(2)某公司希望用50万元承包这项工程,该单位认为金额太高需要降价,通过两次协商,最终以32万元达成一致.若两次降价的百分率相同,求每次降价的百分率.
9.如图,某工程队在工地利用互相垂直的两面墙AE、AF,另两边用铁栅栏围成一个长方形场地ABCD,中间再用铁栅栏分割成两个长方形,铁栅栏总长180米,已知墙AE长90米,墙AF长为60米.
(1)设BC=x米,则CD为 米,四边形ABCD的面积为 米2;
(2)若长方形ABCD的面积为4000平方米,问BC为多少米?
10.如图,学校为美化环境,在靠墙的一侧设计了一块矩形花圃ABCD,其中,墙长19m,花圃三边外围用篱笆围起,共用篱笆30m.
(1)若花圃的面积为100m2,求花圃一边AB的长;
(2)花圃的面积能达到120m2吗?说明理由.
11.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
12.为培养学生正确的劳动价值观和良好的劳动品质.某校为此规划出矩形苗圃ABCD.苗圃的一面靠墙(墙最大可用长度为15米)另三边用木栏围成,中间也用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留1米宽的门(门不用木栏),修建所用木栏总长28米,设矩形ABCD的一边CD长为x米.
(1)矩形ABCD的面积为72m2,求出AB的长.
(2)矩形ABCD的面积能否为80m2,若能,请求出AB的长;若不能,请说明理由.
13.如图,某小区矩形绿地的长宽分别为35m,15m.现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地.
(1)若扩充后的矩形绿地面积为800m2,求新的矩形绿地的长与宽;
(2)扩充后,实地测量发现新的矩形绿地的长宽之比为5:3.求新的矩形绿地面积.
14.如图,在长为50m、宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260m2,道路的宽应为多少?
15.为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图),生态园一面靠墙(墙足够长),另外三面用18m的篱笆围成.生态园的面积能否为40m2?如果能,请求出AB的长;如果不能,请说明理由.
16.如图,老李想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个2m宽的门(建在EF处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为640m2的羊圈?
(2)羊圈的面积能达到650m2吗?如果能,请你给出设计方案;如果不能,请说明理由.
17.如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s,2cm/s的速度从点A,C同时出发,沿规定路线移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,问经过多长时间P,Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
参考答案
一、选择题
1.【解答】解:设花带的宽度为xm,则可列方程为(30﹣2x)(20﹣x)=×20×30,
故选:D.
二、填空题
2.【解答】解:∵道路的宽应为x米,
∴由题意得,(12﹣x)(8﹣x)=77,
故答案为:(12﹣x)(8﹣x)=77.
三、解答题
3.【解答】解:设小路的宽为xm,依题意有
(40﹣x)(32﹣x)=1140,
整理,得x2﹣72x+140=0.
解得x1=2,x2=70(不合题意,舍去).
答:小路的宽应是2m.
4.【解答】解:设AB的长度为x米,则BC的长度为(100﹣4x)米.
根据题意得 (100﹣4x)x=400,
解得 x1=20,x2=5.
则100﹣4x=20或100﹣4x=80.
∵80>25,
∴x2=5舍去.
即AB=20,BC=20.
答:羊圈的边长AB,BC分别是20米、20米.
5.【解答】解:设小路的宽应为xm,
根据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
6.【解答】解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
7.【解答】解:设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
8.【解答】解:(1)设安全区域的宽度为x米,由题意得,(28+2x)(16+2x)=640
整理得x2+22x﹣48=0,
解得x1=2,x2=﹣24(不符合题意,舍去),
答:安全区域的宽度为2米;
(2)设每次降价的百分率为a,由题意得,
50(1﹣a)2=32,
解得a1=1.8(舍去),a2=0.2=20%,
答:每次降价的百分率为20%.
9.【解答】解:(1)设BC=x米,则CD=(180﹣2x)米.四边形ABCD的面积为x(180﹣2x)米2,
故答案为:(180﹣2x),x(180﹣2x);
(2)由题意,得:x(180﹣2x)=4000,
整理,得:x2﹣90x+2000=0,
解得:x=40或x=50,
当x=40时,180﹣2x=100>90,不符合题意,舍去;
当x=50时,180﹣2x=80<90,符合题意;
答:BC=50米,长方形的面积为4000平方米.
10.【解答】解:(1)设AB的长为x米,
由题意可得:x(30﹣2x)=100,
解得:x1=5,x2=10,
∵30﹣2x≤19,
∴x=10,
答:AB的长为10米;
(2)花圃的面积不能达到120m2.理由如下:
设AB的长为y米,
由题意可得:y(30﹣2y)=120,
∴Δ=225﹣240=﹣15<0,
∴方程无解,
∴花圃的面积不能达到120m2.
11.【解答】解:设小路的宽应为x m,
根据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
12.【解答】解:(1)设AB=x m,则BC=(28+2﹣3x)m,
根据题意得:x(28+2﹣3x)=72,
整理得:x2﹣10x+24=0,
解得:x1=4,x2=6,
当x=4时,28+2﹣3x=28+2﹣3×4=18>15,不符合题意,舍去;
当x=6时,28+2﹣3x=28+2﹣3×6=12<15,符合题意.
答:AB的长为6m;
(2)矩形ABCD的面积不能为80m2,理由如下:
假设矩形ABCD的面积能为80m2,设AB=y m,则BC=(28+2﹣3y)m,
根据题意得:y(28+2﹣3y)=80,
整理得:3y2﹣30y+80=0,
∵Δ=(﹣30)2﹣4×3×80=﹣60<0,
∴原方程没有实数根,
∴假设不成立,即矩形ABCD的面积不能为80m2.
13.【解答】解:(1)设将绿地的长、宽增加x m,则新的矩形绿地的长为(35+x)m,宽为(15+x)m,
根据题意得:(35+x)(15+x)=800,
整理得:x2+50x﹣275=0
解得:x1=5,x2=﹣55(不符合题意,舍去),
∴35+x=35+5=40,15+x=15+5=20.
答:新的矩形绿地的长为40m,宽为20m.
(2)设将绿地的长、宽增加y m,则新的矩形绿地的长为(35+y)m,宽为(15+y)m,
根据题意得:(35+y):(15+y)=5:3,
即3(35+y)=5(15+y),
解得:y=15,
∴(35+y)(15+y)=(35+15)×(15+15)=1500.
答:新的矩形绿地面积为1500m2.
14.【解答】解:设路宽应为x米
根据等量关系列方程得:(50﹣2x)(38﹣2x)=1260,
解得:x=4或40,
40不合题意,舍去,
所以x=4,
答:道路的宽应为4米.
15.【解答】解:生态园的面积能为40m2,理由如下:
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
设AB的长度为x m,则BC的长度为m,
由题意得:x =40,
整理得:x2﹣18x+80=0,
解得:x1=10,x2=8,
∴生态园的面积能为40m2,AB的长为10m或8m.
16.【解答】解:(1)设矩形ABCD的边AB=x m,则边BC=70﹣2x+2=(72﹣2x)m.
根据题意,得x(72﹣2x)=640,
化简,得 x2﹣36x+320=0,
解得 x1=16,x2=20,
当x=16时,72﹣2x=72﹣32=40(m),
当x=20时,72﹣2x=72﹣40=32(m).
答:当羊圈的长为40m,宽为16m或长为32m,宽为20m时,能围成一个面积为640m2 的羊圈;
(2)答:不能,
理由:由题意,得x(72﹣2x)=650,
化简,得 x2﹣36x+325=0,
Δ=(﹣36)2﹣4×325=﹣4<0,
∴一元二次方程没有实数根.
∴羊圈的面积不能达到 650m2.
17.【解答】解:(1)过点P作PE⊥CD于E,
设x秒后,点P和点Q的距离是10cm.(16﹣2x﹣3x)2+62=102,
∴,;
∴经过或,P、Q两点之间的距离是10cm;
(2)连接BQ.设经过ys后△PBQ的面积为12cm2.
①当时,PB=16﹣3y,
∴,即,
解得y=4;
②当<y≤时,BP=3y﹣16,QC=2y,
则,
解得(舍去);
③时,QP=CQ﹣PC=22﹣y,
则,
解得y=18(舍去).
综上所述,经过4秒或6秒,△PBQ的面积为12cm2.
21世纪教育网(www.21cnjy.com)
同课章节目录
