重庆市杨家坪中学2015-2016学年高二下学期第二次月考(期中)数学理试题
文档属性
| 名称 | 重庆市杨家坪中学2015-2016学年高二下学期第二次月考(期中)数学理试题 |  | |
| 格式 | zip | ||
| 文件大小 | 177.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-27 06:35:54 | ||
图片预览



文档简介
2015-2016学年度杨家坪中学校高二(下)第二次月考
数学(理科)试卷
一、选择题(每题5分,共60分)
1.复数z=的虚部为( )
A.2 B.﹣2 C.-3 D.3
2.若一个三位数的十位数数字比个位数字和 ( http: / / www.21cnjy.com )百位数字都大,则称这个数为“凸数”,现从1,2,3,4,5,这五个数字中任取3个数,组成无重复数字的三位数,其中“凸数”有( )
A.120个 B.80个 C.40个 D.20个
3.若曲线的一条切线l与直线垂直,则切线l的方程为 ( )
A. B.
C. D.
4.从5位男教师和3位女教师中选出3位教师,派往郊区3所学校支教,每校1人,要求这3位教师中男、女教师都要有,则不同的选派方案有( )
A.210种 B.270种 C.180种 D.90种
5.已知随机变量X的取值为0,1,2,若,,则=( )
A. B. C. D.
6.如图所示,正弦曲线y=sinx,余弦曲线y=cosx与两直线x=0,x=π所围成的阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.1 B.2 C.2 D.
7.已知随机变量,若~,则分别是( )
A.1和2.4 B.2和2.4 C.2和5.6 D.6和5.6
8.设随机变量ξ服从正态分布N(4,7),若,则a=( )
A.1 B.2 C.3 D.4
9.已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),,则第59个数对是( )
A.(3,8) B.(4,7) C.(4,8) D.(5,7)
10.若对任意实数,有成立,则=( )
A. B.14 C.28 D.
11.5颗骰子同时掷出,共掷100次则至少一次出现全为6点的概率为( )
A. B. C. D.
12.设函数-a ,若不等式≤0有解.则实数的最小值为( )
A. B. C. D.
二、填空题(每题5分,共20分)
13.的二项展开式中,含项的系数是___________.
14.将一个大正方形平均分成9个小正方形, ( http: / / www.21cnjy.com )向大正方形区域随机地投掷一个点(每次都能投中),投中最左侧3个小正方形区域的事件记为A,投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B,则P(A|B)=__________
15.5名实习老师到3个班级参加教育实习活动,则每个班级至少有一名实习老师的方案共有_________种.
16.已知函数()满足,且的导数,则不等式的解集为___________.
三、解答题(17题10分,18—22题每题12分,共70分,要求写出必要的解答过程)
17.(本小题满分10分)已知函数
(1)求的单调递增区间;
(2)若在区间上的最小值为20,求它在该区间上的最大值.
18.(本小题满分12分)
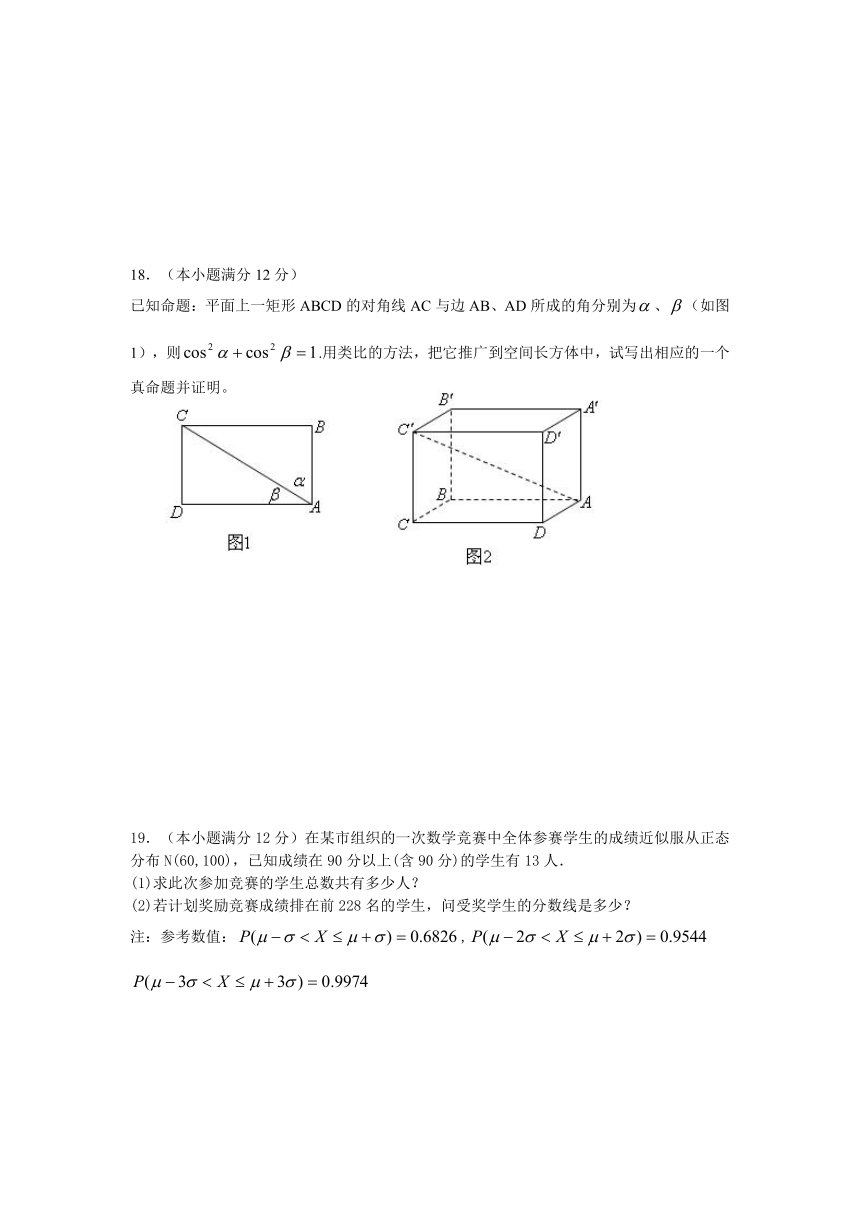
已知命题:平面上一矩形ABCD的对角线AC与边AB、AD所成的角分别为、(如图1),则.用类比的方法,把它推广到空间长方体中,试写出相应的一个真命题并证明。
19.(本小题满分12分)在某市组织的一次 ( http: / / www.21cnjy.com )数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
注:参考数值:,
20.(本小题满分12分)盒中装有7个零件,其中4个是没有使用过的,3个是使用过的.
(Ⅰ)从盒中每次随机抽取1个零件,有放回的抽取3次(不使用),求3次抽取中恰有2次抽到使用过零件的概率;
(Ⅱ)从盒中任意抽取3个零件,使用后放回盒子中,设X为盒子中使用过零件的个数,求X的分布列和期望.
21.(本小题满分12分)已知一个袋内有5只不同的红球,6只不同的白球。
(1)从中任取4只球,红球的只数不比白球少的取法有多少种?
(2)若取一只红球记2分,取一只白球记1分,从中任取5只球,使总分不小于7分的取法有多少种
(3)在(2)条件下,当总分为8时,将抽出的球排成一排,仅有两个红球相邻的排法种数是多少?
22.(本小题满分12分)已知函数(),其导函数为.
(1)求函数的极值;
(2)当时,关于的不等式恒成立,求的取值范围.
.
参考答案
一、选择题
1.D2.D3.C4.B5.C6.B
7.A
试题分析:∵~,∴,,∵,∴,,故选A.
8.D
试题分析:∵随机变量ξ服从正态分布,∵,∴与关于4对称,∴a+2+a-2=8∴2a=8,∴4,故选D.
9.C
试题分析::(1,1),两 ( http: / / www.21cnjy.com )数的和为2,共1个,(1,2),(2,1),两数的和为3,共2个,(1,3),(2,2),(3,1),两数的和为4,共3个,(1,4),(2,3),(3,2),(4,1),两数的和为5,共4个 … ∵1+2+3+4+5+6+7+8+9+10=55,∴第59个数对在第11组之中的第5个数,从而两数之和为12,应为(4,8).10.B
11.D
【解析】5颗骰子同时掷出,没有全部出现6点的概率是,共掷100次至少一次出现全为6点的概率是.
12.A
试题分析:化简≤0可得从而令 ,求导以确定函数的单调性,从而解得.
≤0可化为 , 令,则
故当,即时,有最小值,
故当时,时,;故有最小值 ,故实数的最小值为,故选A
二、填空题
13.-84 14.
试题分析:将一个大正方形平均分成9个小正方形,向大正方形区域随机地投掷一个点(每次都能投中),有9个不同的基本结果,由于是随机投掷的,且小正方形面积大小相等,所以每个结果出现的可能性是相等的,而事件包含4个基本结果,事件包含1个基本结果.
所以,,所以, ( http: / / www.21cnjy.com ).
故答案填:
15.150
16.
试题分析:设根据题意可得函数在R上单调递减,然后根据可得,最后根据单调性可求出x的取值范围.
设,,
即函数F(x)在R上单调递减,,
而函数F(x)在R上单调递减,,即,
故答案为:
三、解答题
17.(1)(-∞,-3),(1,+∞);(2)47
试题解析:(1)f’(x)=3x2+6x-9.令f ‘(x)>0,解得x<-3或x>1,
所以函数f(x)的单调递增区间为(-∞,-3),(1,+∞).
(2)因为f(-2)=22+a,f(2)=20+a,
所以f(-2)>f(2).因为在(-3 ( http: / / www.21cnjy.com ),3)上f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是有 22+a=20,解得 a=-2.
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最大值为-7.
18.命题:长方体中,对角线与棱、、所成的角分别为,则。
证明见解析。
有如下命题:长方体中,对角线与棱、、所成的角分别为,则 …………………………4分
证明:∵,K^S*5U.C#O,
……10分
∴ ………13分
19.(1) 10000人 (2) 80分
解:(1)设学生的成绩为X,共有n人参加竞赛,
∵X~N(60,100),∴μ=60,σ=10.
∴P(X≥90)=[1-P(30<X<90)]=(1-0.9974)=0.0013.
又P(X≥90)=,∴=0.0013.∴n=10000.
故此次参加竞赛的学生总数共有10000人.
(2)设受奖的学生的分数线为x0.则P(X≥x0)==0.0228.
∵0.0228<0.5,∴x0>60.∴P(120-x0<X<x0)=1-2P(X≥x0)=0.9544,
∴x0=60+20=80.故受奖学生的分数线是80分
20.(Ⅰ);(Ⅱ)详见解析.
试题解析:解:(Ⅰ)记“从盒中随机抽取一个零件,抽到的是使用过零件”为事件A.1分
则. 3分
所以三次抽取中恰有2次抽到使用过零件的概率.5分
(Ⅱ)从盒中任意抽取三个零件,使用后放回盒子中,设此时盒子中使用过的零件个数为X,
由已知X=3,4,5, 6 7分
;;
. 10分
随机变量X的分布列为:
X 3 4 5 6
P
11分
E(X)=. 12分
21.(1)215;(2)381;(3)10800。
22.(1)有极大值,无极小值;(2)
试题解析:(1)由题知,,则,,当时,,为增函数;当时,,为减函数.
所以当时,有极大值,无极小值.
(2)由题意,,
(I)当时,在时恒成立,则在上单调递增,所以在上恒成立,与已知矛盾,故不符合题意.
(II)当时,令,则,且.
①当,即时,,于是在上单调递减,
所以,即在上恒成立.
则在上单调递减,所以在上成立,符合题意.
②当,即时,,,
若,则,在上单调递增;
若,则,在上单调递减.
又,所以在上恒成立,即在上恒成立,
所以在上单调递增,则在上恒成立,
所以不符合题意.
综上所述,的取值范围为.
数学(理科)试卷
一、选择题(每题5分,共60分)
1.复数z=的虚部为( )
A.2 B.﹣2 C.-3 D.3
2.若一个三位数的十位数数字比个位数字和 ( http: / / www.21cnjy.com )百位数字都大,则称这个数为“凸数”,现从1,2,3,4,5,这五个数字中任取3个数,组成无重复数字的三位数,其中“凸数”有( )
A.120个 B.80个 C.40个 D.20个
3.若曲线的一条切线l与直线垂直,则切线l的方程为 ( )
A. B.
C. D.
4.从5位男教师和3位女教师中选出3位教师,派往郊区3所学校支教,每校1人,要求这3位教师中男、女教师都要有,则不同的选派方案有( )
A.210种 B.270种 C.180种 D.90种
5.已知随机变量X的取值为0,1,2,若,,则=( )
A. B. C. D.
6.如图所示,正弦曲线y=sinx,余弦曲线y=cosx与两直线x=0,x=π所围成的阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.1 B.2 C.2 D.
7.已知随机变量,若~,则分别是( )
A.1和2.4 B.2和2.4 C.2和5.6 D.6和5.6
8.设随机变量ξ服从正态分布N(4,7),若,则a=( )
A.1 B.2 C.3 D.4
9.已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),,则第59个数对是( )
A.(3,8) B.(4,7) C.(4,8) D.(5,7)
10.若对任意实数,有成立,则=( )
A. B.14 C.28 D.
11.5颗骰子同时掷出,共掷100次则至少一次出现全为6点的概率为( )
A. B. C. D.
12.设函数-a ,若不等式≤0有解.则实数的最小值为( )
A. B. C. D.
二、填空题(每题5分,共20分)
13.的二项展开式中,含项的系数是___________.
14.将一个大正方形平均分成9个小正方形, ( http: / / www.21cnjy.com )向大正方形区域随机地投掷一个点(每次都能投中),投中最左侧3个小正方形区域的事件记为A,投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B,则P(A|B)=__________
15.5名实习老师到3个班级参加教育实习活动,则每个班级至少有一名实习老师的方案共有_________种.
16.已知函数()满足,且的导数,则不等式的解集为___________.
三、解答题(17题10分,18—22题每题12分,共70分,要求写出必要的解答过程)
17.(本小题满分10分)已知函数
(1)求的单调递增区间;
(2)若在区间上的最小值为20,求它在该区间上的最大值.
18.(本小题满分12分)
已知命题:平面上一矩形ABCD的对角线AC与边AB、AD所成的角分别为、(如图1),则.用类比的方法,把它推广到空间长方体中,试写出相应的一个真命题并证明。
19.(本小题满分12分)在某市组织的一次 ( http: / / www.21cnjy.com )数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
注:参考数值:,
20.(本小题满分12分)盒中装有7个零件,其中4个是没有使用过的,3个是使用过的.
(Ⅰ)从盒中每次随机抽取1个零件,有放回的抽取3次(不使用),求3次抽取中恰有2次抽到使用过零件的概率;
(Ⅱ)从盒中任意抽取3个零件,使用后放回盒子中,设X为盒子中使用过零件的个数,求X的分布列和期望.
21.(本小题满分12分)已知一个袋内有5只不同的红球,6只不同的白球。
(1)从中任取4只球,红球的只数不比白球少的取法有多少种?
(2)若取一只红球记2分,取一只白球记1分,从中任取5只球,使总分不小于7分的取法有多少种
(3)在(2)条件下,当总分为8时,将抽出的球排成一排,仅有两个红球相邻的排法种数是多少?
22.(本小题满分12分)已知函数(),其导函数为.
(1)求函数的极值;
(2)当时,关于的不等式恒成立,求的取值范围.
.
参考答案
一、选择题
1.D2.D3.C4.B5.C6.B
7.A
试题分析:∵~,∴,,∵,∴,,故选A.
8.D
试题分析:∵随机变量ξ服从正态分布,∵,∴与关于4对称,∴a+2+a-2=8∴2a=8,∴4,故选D.
9.C
试题分析::(1,1),两 ( http: / / www.21cnjy.com )数的和为2,共1个,(1,2),(2,1),两数的和为3,共2个,(1,3),(2,2),(3,1),两数的和为4,共3个,(1,4),(2,3),(3,2),(4,1),两数的和为5,共4个 … ∵1+2+3+4+5+6+7+8+9+10=55,∴第59个数对在第11组之中的第5个数,从而两数之和为12,应为(4,8).10.B
11.D
【解析】5颗骰子同时掷出,没有全部出现6点的概率是,共掷100次至少一次出现全为6点的概率是.
12.A
试题分析:化简≤0可得从而令 ,求导以确定函数的单调性,从而解得.
≤0可化为 , 令,则
故当,即时,有最小值,
故当时,时,;故有最小值 ,故实数的最小值为,故选A
二、填空题
13.-84 14.
试题分析:将一个大正方形平均分成9个小正方形,向大正方形区域随机地投掷一个点(每次都能投中),有9个不同的基本结果,由于是随机投掷的,且小正方形面积大小相等,所以每个结果出现的可能性是相等的,而事件包含4个基本结果,事件包含1个基本结果.
所以,,所以, ( http: / / www.21cnjy.com ).
故答案填:
15.150
16.
试题分析:设根据题意可得函数在R上单调递减,然后根据可得,最后根据单调性可求出x的取值范围.
设,,
即函数F(x)在R上单调递减,,
而函数F(x)在R上单调递减,,即,
故答案为:
三、解答题
17.(1)(-∞,-3),(1,+∞);(2)47
试题解析:(1)f’(x)=3x2+6x-9.令f ‘(x)>0,解得x<-3或x>1,
所以函数f(x)的单调递增区间为(-∞,-3),(1,+∞).
(2)因为f(-2)=22+a,f(2)=20+a,
所以f(-2)>f(2).因为在(-3 ( http: / / www.21cnjy.com ),3)上f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是有 22+a=20,解得 a=-2.
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最大值为-7.
18.命题:长方体中,对角线与棱、、所成的角分别为,则。
证明见解析。
有如下命题:长方体中,对角线与棱、、所成的角分别为,则 …………………………4分
证明:∵,K^S*5U.C#O,
……10分
∴ ………13分
19.(1) 10000人 (2) 80分
解:(1)设学生的成绩为X,共有n人参加竞赛,
∵X~N(60,100),∴μ=60,σ=10.
∴P(X≥90)=[1-P(30<X<90)]=(1-0.9974)=0.0013.
又P(X≥90)=,∴=0.0013.∴n=10000.
故此次参加竞赛的学生总数共有10000人.
(2)设受奖的学生的分数线为x0.则P(X≥x0)==0.0228.
∵0.0228<0.5,∴x0>60.∴P(120-x0<X<x0)=1-2P(X≥x0)=0.9544,
∴x0=60+20=80.故受奖学生的分数线是80分
20.(Ⅰ);(Ⅱ)详见解析.
试题解析:解:(Ⅰ)记“从盒中随机抽取一个零件,抽到的是使用过零件”为事件A.1分
则. 3分
所以三次抽取中恰有2次抽到使用过零件的概率.5分
(Ⅱ)从盒中任意抽取三个零件,使用后放回盒子中,设此时盒子中使用过的零件个数为X,
由已知X=3,4,5, 6 7分
;;
. 10分
随机变量X的分布列为:
X 3 4 5 6
P
11分
E(X)=. 12分
21.(1)215;(2)381;(3)10800。
22.(1)有极大值,无极小值;(2)
试题解析:(1)由题知,,则,,当时,,为增函数;当时,,为减函数.
所以当时,有极大值,无极小值.
(2)由题意,,
(I)当时,在时恒成立,则在上单调递增,所以在上恒成立,与已知矛盾,故不符合题意.
(II)当时,令,则,且.
①当,即时,,于是在上单调递减,
所以,即在上恒成立.
则在上单调递减,所以在上成立,符合题意.
②当,即时,,,
若,则,在上单调递增;
若,则,在上单调递减.
又,所以在上恒成立,即在上恒成立,
所以在上单调递增,则在上恒成立,
所以不符合题意.
综上所述,的取值范围为.
同课章节目录
