16.3 二次根式的加减 课时1 课件 (共49张PPT) 2024--2025学年人教版八年级下册数学
文档属性
| 名称 | 16.3 二次根式的加减 课时1 课件 (共49张PPT) 2024--2025学年人教版八年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览










文档简介
(共49张PPT)
第十六章 二次根式
16.3 二次根式的加减
课时1 二次根式的加减
新课讲解
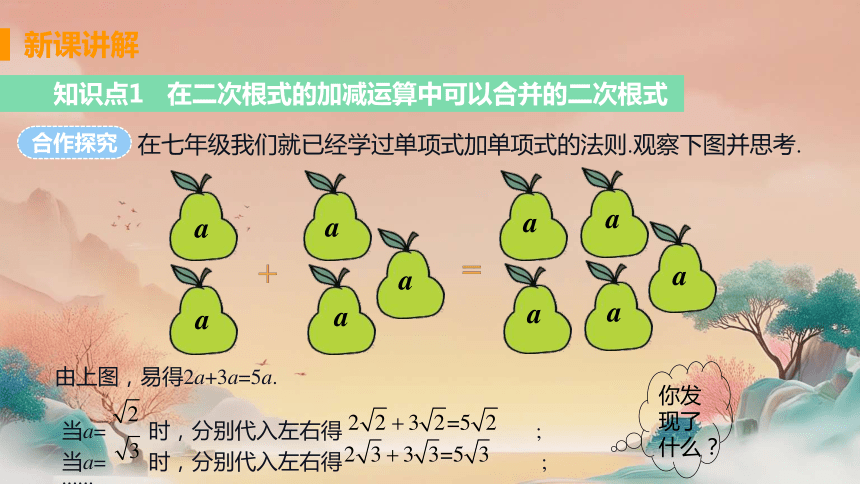
知识点1 在二次根式的加减运算中可以合并的二次根式
合作探究
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;
......
你发现了什么?
新课讲解
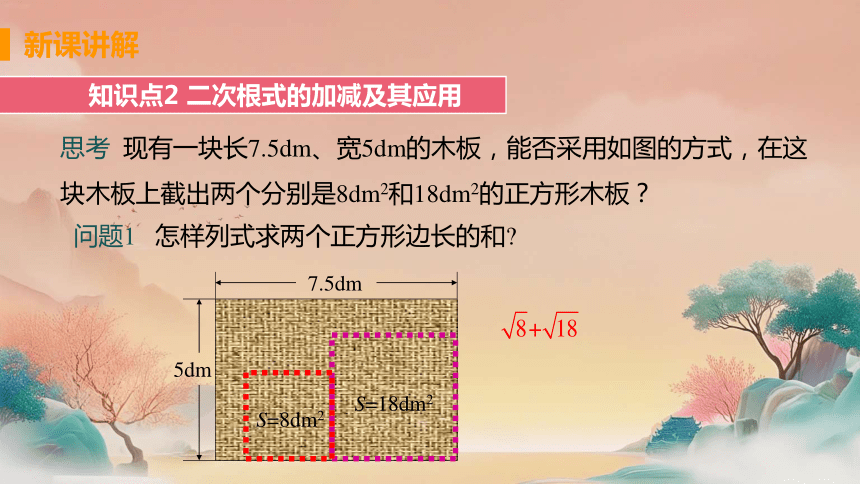
知识点2 二次根式的加减及其应用
思考 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
问题1 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
新课讲解
归纳总结
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
新课讲解
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
新课讲解
二次根式的加减与等腰三角形的综合运用,关键是要分类讨论及会比较两个二次根式的大小.
归纳
课堂小结
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
当堂小练
1.三角形的三边长分别为 则这个三角形的周长为__________.
2.计算:
(1)将二次根式化成最简二次根式,若 相同,则这样的二次根式可以合并.
(2)合并的方法与合并同类项类似,把根号外的因数(式) ,根指数和被开方数不变.
(3)合并的依据是乘法分配律,如:
m+n=(m+n).
可以合并的二次根式
被开方数
相加
1.(2024广西一模)下列二次根式中,与可以合并的是
( )
A. B.
C. D.
C
2.(1)在二次根式中,可以与合并的是
;
(2)(2024揭阳二模)若最简二次根式与能够合并,则m= .
2
(1)二次根式加减时,先将二次根式化成最简二次根式,再将被开方数 的二次根式进行合并.
(2)二次根式的加减的运算步骤
①化成最简二次根式;
②找出被开方数相同的二次根式;
③合并被开方数相同的二次根式.
二次根式的加减及运算步骤
相同
(3)注意事项
①在运算过程中要注意,根号外的因式就是这个二次根式的系数,如果系数是带分数,还要化成假分数;
②被开方数不同的二次根式不能合并,但是绝不能丢弃,它们也是结果的一部分;
③在进行二次根式的加减运算时,整式加法的交换律、结合律及去括号、添括号法则仍然适用.
3.(人教8下P13)下列计算是否正确
(1)-=;
(2)+=;
(3)3-=2.
不正确
不正确
正确
4.(人教8下P12)计算:
+
= (化成最简二次根式)
= (分配律)
= .
2+3
(2+3)
5
5.计算:
(1)+; (2)-;
(3)2+5-7; (4)3-(+).
(1)3
(2)2
(3)0
(4)2-
6.【例1】计算:
(1)+; (2)-.
解:(1)原式=3+2=5.
(2)原式=2-=.
小结:按步骤进行二次根式的加减运算,可记为:一化二看
三合并.
7.【例2】计算:
(1)2-7+4; (2)--.
解:(1)原式=2-7+4
=2-14+12=(2-14+12)=0.
(2)原式=3--2=-.
小结:(1)二次根式的加减运算的实质就是合并被开方数相同的二次根式;(2)正确地化简二次根式及准确地判断被开方数相同的二次根式是解题的关键.
9.(人教8下P13、北师8上P44改编)计算:
(1)-; (2)+.
解:(1)原式=4 -3 =.
(2)原式=3 +5 =8 .
10.(人教8下P13、北师8上P47改编)计算:
(1)2-6+3; (2)(+)+(-).
解:(1)原式=4 -2 +12 =14 .
(2)原式=2 +2 +-=3 +.
8.【例3】(人教8下P15、北师8上P46改编)(运算能力)已知≈2.236,求5-+的近似值(结果保留小数点后两位).
解:5-+=-+3=≈≈7.83.
小结:根据已知,所求的式子在化简后应与有关.
★11. (创新题)若a,b为有理数,且-+=a+b,求a+b的值.
0.55
解:-+=2-3+=2-=a+b,
∴a=2,b=-,∴a+b=-.
新课讲解
知识点1 二次根式的混合运算及应用
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
例1 计算:
解:
新课讲解
知识点2 利用乘法公式进行二次根式的运算
问题1 整式乘法运算中的乘法公式有哪些
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
问题2 整式的乘法公式对于二次根式的运算也适用吗
整式的乘法公式就是多项式×多项式
前面我们已经知道二次根式运算类比整式运算,所以适用哟
新课讲解
计算:
练一练
先用乘法交换律,再用乘法公式化简.
课堂小结
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
当堂小练
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
当堂小练
1.下列计算中正确的是( )
B
2.计算:
5
3.设 则a b(填“>”“ < ”或 “= ”).
=
(1)二次根式的混合运算是指二次根式的加、减、乘、除、
的混合运算.
(2)二次根式的混合运算顺序
二次根式的混合运算顺序与实数的混合运算顺序一样,先算
,再算 ,最后算 ,有括号的先算括号内的运算(或先去掉括号).
二次根式的混合运算及运算顺序
乘方
乘方
乘除
加减
(3)口诀
二次根式混合算,弄清顺序是关键,
先乘方来后乘除,最后再去算加减.
1.按下列步骤计算:
10÷+3
=10÷5+3
= +3
= .
2
5
2.计算:×+÷.
解:原式=2+=3.
(1)二次根式混合运算的结果应写成最简二次根式的形式.
(2)在二次根式的混合运算中,实数的运算律、多项式的乘法法则、多项式的乘法公式仍然适用.
二次根式的混合运算中的乘法法则及乘法公式应用
(3)回顾多项式的乘法公式
平方差公式:(a+b)(a-b)= .
完全平方公式:
(a+b)2= ,
(a-b)2= .
a2-b2
a2+2ab+b2
a2-2ab+b2
3.(人教8下P14、北师8上P44改编)计算:
(1)(+)×; (2)(4 -3 )÷2 .
解:(1)原式=×+×=4 +3 .
(2)原式=4 ÷2 -3 ÷2 =2- .
4.(人教8下P14)计算:(+3)(+2).
解:原式=()2+2+3+6
=5+5+6=11+5.
5.按下列步骤计算:
(1)(+)(-)
=( )2 -( )2 = ;
(2)
=+ += .
1
2××
5+2
6.【例1】计算:
(1)×; (2)(-)÷.
解:(1)原式=-=9-1=8.
(2)原式=-=2-3=-1.
小结:根据多项式乘单项式、多项式除以单项式的法则进行计算.
7.【例2】(人教8下P14)计算:
(1)(+3)(-5); (2)(+)(-);
解:(1)原式=()2-5+3-15
=2-2-15=-13-2.
(2)原式=()2-()2=5-3=2.
(3)(+2)2; (4)(2-)2.
解:(3)原式=()2+2××2+22
=3+4+4=7+4.
(4)原式=(2)2-2×2×+()2
=20-4+2=22-4.
小结:能用乘法公式的尽量使用乘法公式,可简化计算过程.
8.【例3】计算:
(-1)×+(2-2)÷.
解:原式=2-+2-2=.
小结:正确掌握二次根式的混合运算法则是解题关键.
9.【例4】(2024沈阳一模)已知a=2+,b=2-,求代数式a2b-ab2的值.
解:原式=ab(a-b)
=(2+)(2-)(2+-2+)
=[22-()2]×2
=-1×2
=-2.
小结:灵活运用因式分解,再代入求值.
10.(人教8下P14)计算:
(1)(+); (2)(+)÷.
解:(1)原式=+.
(2)原式=+=4+2 .
11.(北师8上P44-45)计算:
(1)(3+)(-2); (2)(+3)(-3);
解:(1)原式=3-6+5-2=-1.
(2)原式=()2-32=13-9=4.
(3)(+)2; (4)(2-1)2.
解:(3)原式=()2+2××+()2
=2+2+5=7+2.
(4)原式=(2)2-2×2×1+1
=12-4+1=13-4.
12.(人教8下P15)计算:
(+)-(+).
解:原式=+--
=+=--.
★13. (运算能力)(2024杭州模拟)已知a=3-,b=-1,求-的值.
0.50
解:∵b=-1,
∴b2=(-1)2=5-2+1=6-2=2(3-),
∵a=3-,
∴b2=2a,
∴原式=-=-2=-.
请完成本节课后对应习题
布置作业
第十六章 二次根式
16.3 二次根式的加减
课时1 二次根式的加减
新课讲解
知识点1 在二次根式的加减运算中可以合并的二次根式
合作探究
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;
......
你发现了什么?
新课讲解
知识点2 二次根式的加减及其应用
思考 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
问题1 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
新课讲解
归纳总结
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
新课讲解
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
新课讲解
二次根式的加减与等腰三角形的综合运用,关键是要分类讨论及会比较两个二次根式的大小.
归纳
课堂小结
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
当堂小练
1.三角形的三边长分别为 则这个三角形的周长为__________.
2.计算:
(1)将二次根式化成最简二次根式,若 相同,则这样的二次根式可以合并.
(2)合并的方法与合并同类项类似,把根号外的因数(式) ,根指数和被开方数不变.
(3)合并的依据是乘法分配律,如:
m+n=(m+n).
可以合并的二次根式
被开方数
相加
1.(2024广西一模)下列二次根式中,与可以合并的是
( )
A. B.
C. D.
C
2.(1)在二次根式中,可以与合并的是
;
(2)(2024揭阳二模)若最简二次根式与能够合并,则m= .
2
(1)二次根式加减时,先将二次根式化成最简二次根式,再将被开方数 的二次根式进行合并.
(2)二次根式的加减的运算步骤
①化成最简二次根式;
②找出被开方数相同的二次根式;
③合并被开方数相同的二次根式.
二次根式的加减及运算步骤
相同
(3)注意事项
①在运算过程中要注意,根号外的因式就是这个二次根式的系数,如果系数是带分数,还要化成假分数;
②被开方数不同的二次根式不能合并,但是绝不能丢弃,它们也是结果的一部分;
③在进行二次根式的加减运算时,整式加法的交换律、结合律及去括号、添括号法则仍然适用.
3.(人教8下P13)下列计算是否正确
(1)-=;
(2)+=;
(3)3-=2.
不正确
不正确
正确
4.(人教8下P12)计算:
+
= (化成最简二次根式)
= (分配律)
= .
2+3
(2+3)
5
5.计算:
(1)+; (2)-;
(3)2+5-7; (4)3-(+).
(1)3
(2)2
(3)0
(4)2-
6.【例1】计算:
(1)+; (2)-.
解:(1)原式=3+2=5.
(2)原式=2-=.
小结:按步骤进行二次根式的加减运算,可记为:一化二看
三合并.
7.【例2】计算:
(1)2-7+4; (2)--.
解:(1)原式=2-7+4
=2-14+12=(2-14+12)=0.
(2)原式=3--2=-.
小结:(1)二次根式的加减运算的实质就是合并被开方数相同的二次根式;(2)正确地化简二次根式及准确地判断被开方数相同的二次根式是解题的关键.
9.(人教8下P13、北师8上P44改编)计算:
(1)-; (2)+.
解:(1)原式=4 -3 =.
(2)原式=3 +5 =8 .
10.(人教8下P13、北师8上P47改编)计算:
(1)2-6+3; (2)(+)+(-).
解:(1)原式=4 -2 +12 =14 .
(2)原式=2 +2 +-=3 +.
8.【例3】(人教8下P15、北师8上P46改编)(运算能力)已知≈2.236,求5-+的近似值(结果保留小数点后两位).
解:5-+=-+3=≈≈7.83.
小结:根据已知,所求的式子在化简后应与有关.
★11. (创新题)若a,b为有理数,且-+=a+b,求a+b的值.
0.55
解:-+=2-3+=2-=a+b,
∴a=2,b=-,∴a+b=-.
新课讲解
知识点1 二次根式的混合运算及应用
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
例1 计算:
解:
新课讲解
知识点2 利用乘法公式进行二次根式的运算
问题1 整式乘法运算中的乘法公式有哪些
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
问题2 整式的乘法公式对于二次根式的运算也适用吗
整式的乘法公式就是多项式×多项式
前面我们已经知道二次根式运算类比整式运算,所以适用哟
新课讲解
计算:
练一练
先用乘法交换律,再用乘法公式化简.
课堂小结
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
当堂小练
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
当堂小练
1.下列计算中正确的是( )
B
2.计算:
5
3.设 则a b(填“>”“ < ”或 “= ”).
=
(1)二次根式的混合运算是指二次根式的加、减、乘、除、
的混合运算.
(2)二次根式的混合运算顺序
二次根式的混合运算顺序与实数的混合运算顺序一样,先算
,再算 ,最后算 ,有括号的先算括号内的运算(或先去掉括号).
二次根式的混合运算及运算顺序
乘方
乘方
乘除
加减
(3)口诀
二次根式混合算,弄清顺序是关键,
先乘方来后乘除,最后再去算加减.
1.按下列步骤计算:
10÷+3
=10÷5+3
= +3
= .
2
5
2.计算:×+÷.
解:原式=2+=3.
(1)二次根式混合运算的结果应写成最简二次根式的形式.
(2)在二次根式的混合运算中,实数的运算律、多项式的乘法法则、多项式的乘法公式仍然适用.
二次根式的混合运算中的乘法法则及乘法公式应用
(3)回顾多项式的乘法公式
平方差公式:(a+b)(a-b)= .
完全平方公式:
(a+b)2= ,
(a-b)2= .
a2-b2
a2+2ab+b2
a2-2ab+b2
3.(人教8下P14、北师8上P44改编)计算:
(1)(+)×; (2)(4 -3 )÷2 .
解:(1)原式=×+×=4 +3 .
(2)原式=4 ÷2 -3 ÷2 =2- .
4.(人教8下P14)计算:(+3)(+2).
解:原式=()2+2+3+6
=5+5+6=11+5.
5.按下列步骤计算:
(1)(+)(-)
=( )2 -( )2 = ;
(2)
=+ += .
1
2××
5+2
6.【例1】计算:
(1)×; (2)(-)÷.
解:(1)原式=-=9-1=8.
(2)原式=-=2-3=-1.
小结:根据多项式乘单项式、多项式除以单项式的法则进行计算.
7.【例2】(人教8下P14)计算:
(1)(+3)(-5); (2)(+)(-);
解:(1)原式=()2-5+3-15
=2-2-15=-13-2.
(2)原式=()2-()2=5-3=2.
(3)(+2)2; (4)(2-)2.
解:(3)原式=()2+2××2+22
=3+4+4=7+4.
(4)原式=(2)2-2×2×+()2
=20-4+2=22-4.
小结:能用乘法公式的尽量使用乘法公式,可简化计算过程.
8.【例3】计算:
(-1)×+(2-2)÷.
解:原式=2-+2-2=.
小结:正确掌握二次根式的混合运算法则是解题关键.
9.【例4】(2024沈阳一模)已知a=2+,b=2-,求代数式a2b-ab2的值.
解:原式=ab(a-b)
=(2+)(2-)(2+-2+)
=[22-()2]×2
=-1×2
=-2.
小结:灵活运用因式分解,再代入求值.
10.(人教8下P14)计算:
(1)(+); (2)(+)÷.
解:(1)原式=+.
(2)原式=+=4+2 .
11.(北师8上P44-45)计算:
(1)(3+)(-2); (2)(+3)(-3);
解:(1)原式=3-6+5-2=-1.
(2)原式=()2-32=13-9=4.
(3)(+)2; (4)(2-1)2.
解:(3)原式=()2+2××+()2
=2+2+5=7+2.
(4)原式=(2)2-2×2×1+1
=12-4+1=13-4.
12.(人教8下P15)计算:
(+)-(+).
解:原式=+--
=+=--.
★13. (运算能力)(2024杭州模拟)已知a=3-,b=-1,求-的值.
0.50
解:∵b=-1,
∴b2=(-1)2=5-2+1=6-2=2(3-),
∵a=3-,
∴b2=2a,
∴原式=-=-2=-.
请完成本节课后对应习题
布置作业
