【专项培优】沪科版数学八年级下册第18章勾股定理(含答案)
文档属性
| 名称 | 【专项培优】沪科版数学八年级下册第18章勾股定理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 514.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 09:02:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【专项培优】沪科版数学八年级下册第18章勾股定理
一、单选题
1.(2019八下·大石桥期中)如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60 m,AC=20 m,则A,B两点间的距离是( )
A.200 m B.40 m C.20 m D.50 m
2.(2024八下·平南期中)如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了( )米,却踩伤了花草.
A.1 B.1.5 C.2 D.3
3.(2016八上·扬州期末)如图,已知1号、4号两个正方形的面积和为10, 2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )
A.17 B.27 C.24 D.34
4.(2023八上·东乡区期中)在中,,,分别是,,的对边,若,则( )
A. B. C. D.
5.(2024八上·太平月考)甲、乙两人玩跑步游戏,两人从同一地点同时出发,甲向西跑了16米,乙向北跑了30米,此时他们两人之间的距离为( )
A.28米 B.30米 C.32米 D.34米
二、填空题
6.(2024八下·张北月考)如图,一次函数的图象与x轴、y轴的交点分别为A、B,则的长为 .
7.(2024七下·重庆市期末)如图,一个圆柱高,底面周长为,一只蚂蚁从点A沿圆柱表面爬到点B处觅食,要爬行的最短路程为 .
8.(2023八上·贵阳期中)如图,在直线上有正方形,,,若,的面积分别为4和16,则的面积为 .
9.(2024九上·高青模拟)如图所示,有一块直角三角形纸片,,将斜边翻折,使点B落在直角边的延长线上的点E处,折痕为,则的长是 .
10.(2024八下·荔城月考)如图,在中,,是边上的中线,,则的面积是 .
11.(2022九下·港北模拟)如图,OP为∠AOB的平分线,PC⊥OB于点C,且,,点P的OA距离为 .
三、计算题
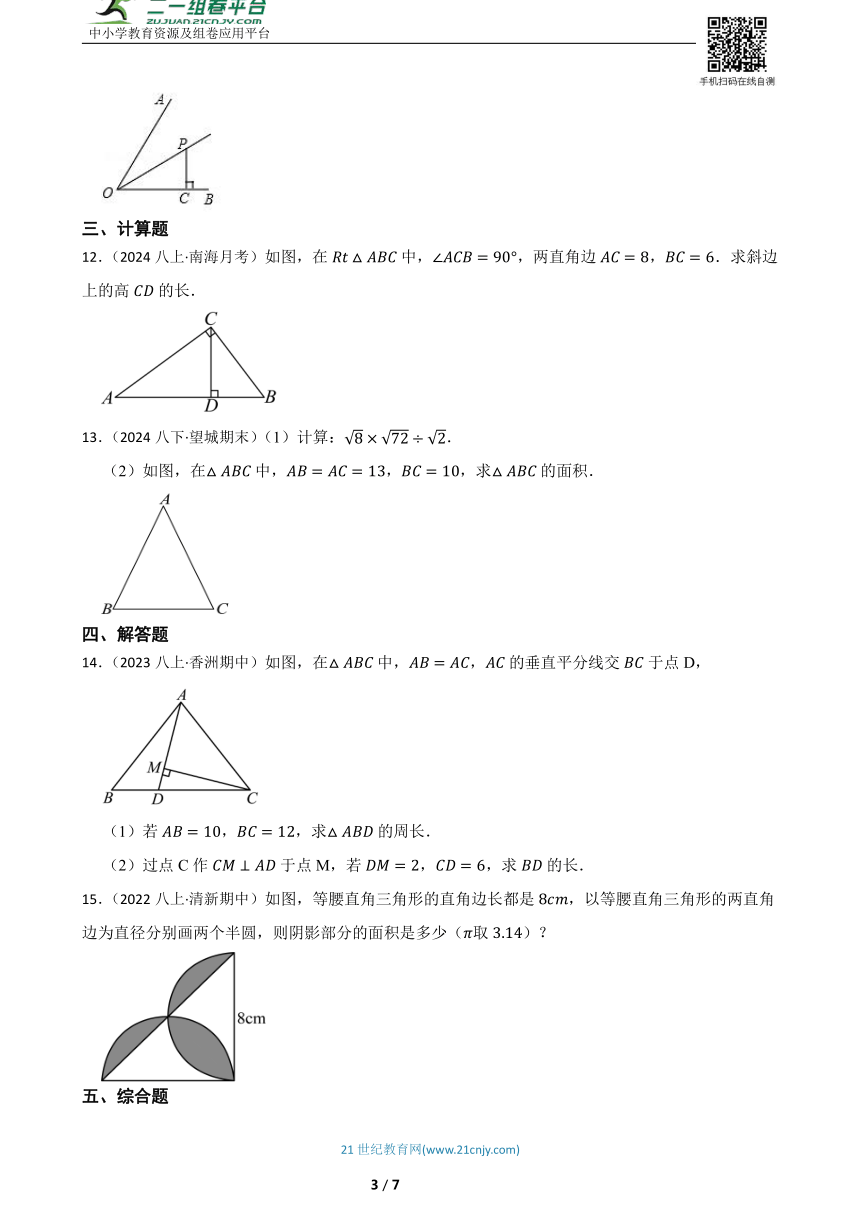
12.(2024八上·南海月考)如图,在中,,两直角边,.求斜边上的高的长.
13.(2024八下·望城期末)(1)计算:.
(2)如图,在中,,,求的面积.
四、解答题
14.(2023八上·香洲期中)如图,在中,,的垂直平分线交于点D,
(1)若,,求的周长.
(2)过点C作于点M,若,,求的长.
15.(2022八上·清新期中)如图,等腰直角三角形的直角边长都是,以等腰直角三角形的两直角边为直径分别画两个半圆,则阴影部分的面积是多少(取)?
五、综合题
16.(2024八下·腾冲期中)《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇生长在它的中央,高出水面部分为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边.求水深和芦苇长各是多少尺?
17.(2024八下·高安期中)小明和小亮学习了“勾股定理”之后,为了测量风筝的垂直高度,他们进行了如下操作:
①测得水平距离的长为15米;
②根据手中剩余线的长度计算出风筝线的长为25米;
③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
18.(2024八上·成都月考)如图,小明在距离水面高度为12米的岸边C处,用绳子拉船靠岸,开始时绳子的长为20米.若小明收绳5米后,船到达D处,则船向岸A移动了多少米?
六、实践探究题
19.(2024八下·互助期末)塔吊是建筑工地上最常用的一种起重设备,又名“塔式起重机”,用来吊施工用的钢筋、木楞、混凝土、钢管等施工的原材料.如图1是塔吊实物图,图2是塔吊示意图,线段,表示钢丝绳,表示起重臂,,综合与实践小组向工人了解到如下信息:米,米,米.求钢丝绳的长度(参考数值:)
答案解析部分
1.【答案】B
【知识点】勾股定理的应用
2.【答案】C
【知识点】勾股定理的应用
3.【答案】C
【知识点】全等三角形的判定与性质;勾股定理
4.【答案】B
【知识点】勾股定理
5.【答案】D
【知识点】勾股定理
6.【答案】5
【知识点】勾股定理;一次函数图象与坐标轴交点问题
7.【答案】
【知识点】勾股定理的实际应用-最短路径问题
8.【答案】12
【知识点】勾股定理
9.【答案】
【知识点】勾股定理
10.【答案】
【知识点】勾股定理的逆定理;三角形全等的判定-SAS
11.【答案】1
【知识点】角平分线的性质;勾股定理
12.【答案】
【知识点】勾股定理
13.【答案】(1);(2)60
【知识点】二次根式的乘除法;等腰三角形的性质;勾股定理
14.【答案】(1)的周长为
(2)
【知识点】线段垂直平分线的性质;勾股定理
15.【答案】
【知识点】勾股定理
16.【答案】水深尺,芦苇长尺
【知识点】勾股定理的应用
17.【答案】(1)21.6米;
(2)应该往回收线8米.
【知识点】勾股定理
18.【答案】7米
【知识点】勾股定理;求算术平方根
19.【答案】36米
【知识点】勾股定理
21世纪教育网(www.21cnjy.com)
1 / 7
【专项培优】沪科版数学八年级下册第18章勾股定理
一、单选题
1.(2019八下·大石桥期中)如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60 m,AC=20 m,则A,B两点间的距离是( )
A.200 m B.40 m C.20 m D.50 m
2.(2024八下·平南期中)如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了( )米,却踩伤了花草.
A.1 B.1.5 C.2 D.3
3.(2016八上·扬州期末)如图,已知1号、4号两个正方形的面积和为10, 2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )
A.17 B.27 C.24 D.34
4.(2023八上·东乡区期中)在中,,,分别是,,的对边,若,则( )
A. B. C. D.
5.(2024八上·太平月考)甲、乙两人玩跑步游戏,两人从同一地点同时出发,甲向西跑了16米,乙向北跑了30米,此时他们两人之间的距离为( )
A.28米 B.30米 C.32米 D.34米
二、填空题
6.(2024八下·张北月考)如图,一次函数的图象与x轴、y轴的交点分别为A、B,则的长为 .
7.(2024七下·重庆市期末)如图,一个圆柱高,底面周长为,一只蚂蚁从点A沿圆柱表面爬到点B处觅食,要爬行的最短路程为 .
8.(2023八上·贵阳期中)如图,在直线上有正方形,,,若,的面积分别为4和16,则的面积为 .
9.(2024九上·高青模拟)如图所示,有一块直角三角形纸片,,将斜边翻折,使点B落在直角边的延长线上的点E处,折痕为,则的长是 .
10.(2024八下·荔城月考)如图,在中,,是边上的中线,,则的面积是 .
11.(2022九下·港北模拟)如图,OP为∠AOB的平分线,PC⊥OB于点C,且,,点P的OA距离为 .
三、计算题
12.(2024八上·南海月考)如图,在中,,两直角边,.求斜边上的高的长.
13.(2024八下·望城期末)(1)计算:.
(2)如图,在中,,,求的面积.
四、解答题
14.(2023八上·香洲期中)如图,在中,,的垂直平分线交于点D,
(1)若,,求的周长.
(2)过点C作于点M,若,,求的长.
15.(2022八上·清新期中)如图,等腰直角三角形的直角边长都是,以等腰直角三角形的两直角边为直径分别画两个半圆,则阴影部分的面积是多少(取)?
五、综合题
16.(2024八下·腾冲期中)《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇生长在它的中央,高出水面部分为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边.求水深和芦苇长各是多少尺?
17.(2024八下·高安期中)小明和小亮学习了“勾股定理”之后,为了测量风筝的垂直高度,他们进行了如下操作:
①测得水平距离的长为15米;
②根据手中剩余线的长度计算出风筝线的长为25米;
③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
18.(2024八上·成都月考)如图,小明在距离水面高度为12米的岸边C处,用绳子拉船靠岸,开始时绳子的长为20米.若小明收绳5米后,船到达D处,则船向岸A移动了多少米?
六、实践探究题
19.(2024八下·互助期末)塔吊是建筑工地上最常用的一种起重设备,又名“塔式起重机”,用来吊施工用的钢筋、木楞、混凝土、钢管等施工的原材料.如图1是塔吊实物图,图2是塔吊示意图,线段,表示钢丝绳,表示起重臂,,综合与实践小组向工人了解到如下信息:米,米,米.求钢丝绳的长度(参考数值:)
答案解析部分
1.【答案】B
【知识点】勾股定理的应用
2.【答案】C
【知识点】勾股定理的应用
3.【答案】C
【知识点】全等三角形的判定与性质;勾股定理
4.【答案】B
【知识点】勾股定理
5.【答案】D
【知识点】勾股定理
6.【答案】5
【知识点】勾股定理;一次函数图象与坐标轴交点问题
7.【答案】
【知识点】勾股定理的实际应用-最短路径问题
8.【答案】12
【知识点】勾股定理
9.【答案】
【知识点】勾股定理
10.【答案】
【知识点】勾股定理的逆定理;三角形全等的判定-SAS
11.【答案】1
【知识点】角平分线的性质;勾股定理
12.【答案】
【知识点】勾股定理
13.【答案】(1);(2)60
【知识点】二次根式的乘除法;等腰三角形的性质;勾股定理
14.【答案】(1)的周长为
(2)
【知识点】线段垂直平分线的性质;勾股定理
15.【答案】
【知识点】勾股定理
16.【答案】水深尺,芦苇长尺
【知识点】勾股定理的应用
17.【答案】(1)21.6米;
(2)应该往回收线8米.
【知识点】勾股定理
18.【答案】7米
【知识点】勾股定理;求算术平方根
19.【答案】36米
【知识点】勾股定理
21世纪教育网(www.21cnjy.com)
1 / 7
