5.2.2 等差数列的前n项和 课件（(2课时，共36张PPT)）

(共36张PPT)
5.2.2
等差数列的前n项和
人教B版(2019)选择性必修第三册
5.2.2 课时1
等差数列的前n项和
人教B版(2019)选择性必修第三册
1.掌握等差数列前项和公式的推导方法．
2.掌握等差数列的前项和公式，能够运用公式解决相关问题．
已知等差数列{an}的首项为a1，公差为d，回答下列问题：
（1）通项公式an= .
（2）如果m+n=p+q(m，n，p，q N+)，则 .
an=a1+(n-1)d
高斯出生于一个工匠家庭，幼时家境贫困，但聪敏异常。上小学四年级时，一次老师布置了一道数学习题：“把从1到100的自然数加起来，和是多少？”年仅10岁的小高斯略一思索就得到答案5050，这使老师非常吃惊.那么高斯是采用了什么方法来巧妙地计算出来的呢？
首项与末项的和： 1＋100＝101，
第2项与倒数第2项的和： 2＋99 =101，
第3项与倒数第3项的和： 3＋98 ＝101，
· · · · · ·
第50项与倒数第50项的和：50＋51＝101，
于是所求的和是：
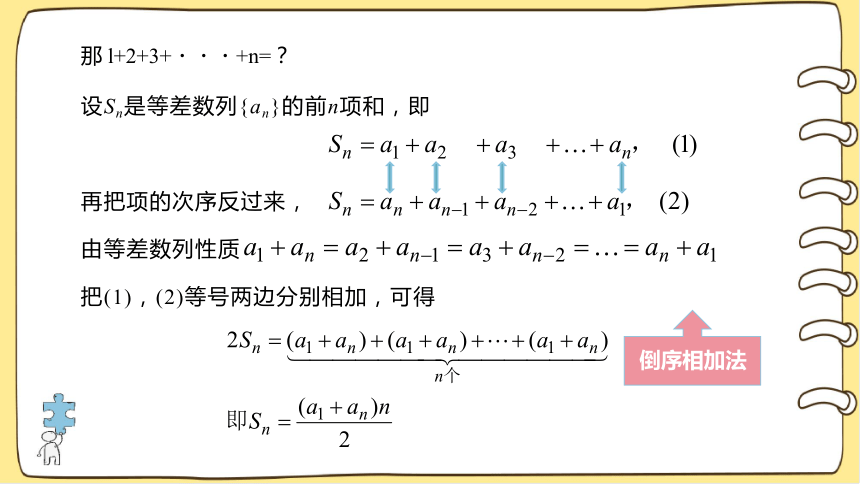
那 l+2+3+ +n=？
设Sn是等差数列{an}的前n项和，即
再把项的次序反过来，
由等差数列性质
把(1)，(2)等号两边分别相加，可得
倒序相加法
首项为a1，末项为an，项数为n的等差数列的前n项和
这个公式表明：等差数列前n项和等于首末两项的和与项数乘积的一半，其原理参见右图.
将an=a1+(n-1)d代入上式，得
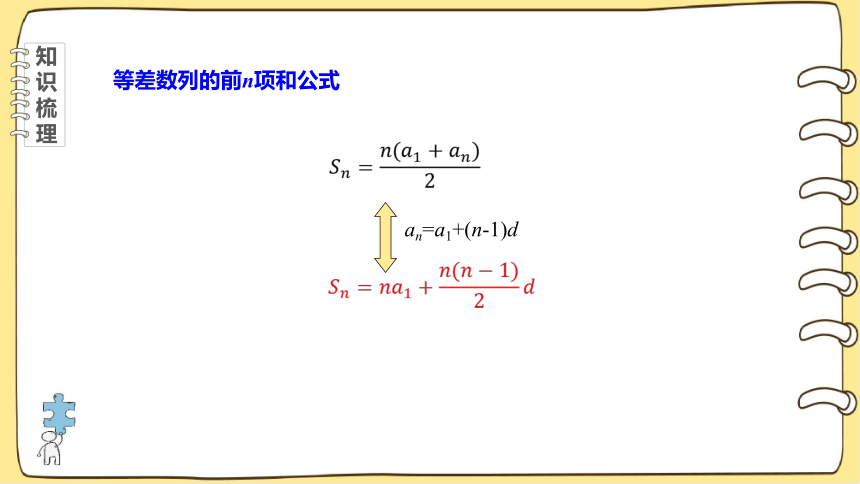
等差数列的前n项和公式
an=a1+(n-1)d
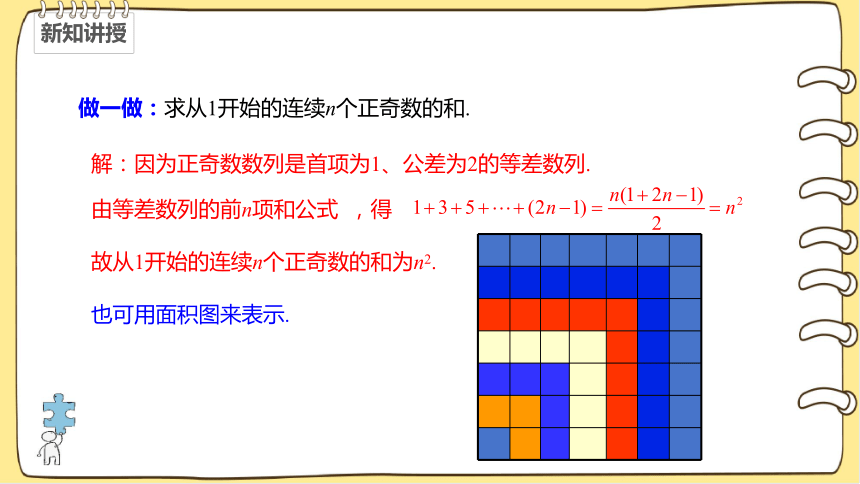
解：因为正奇数数列是首项为1、公差为2的等差数列.
做一做：求从1开始的连续n个正奇数的和.
由等差数列的前n项和公式 ，得
故从1开始的连续n个正奇数的和为n2.
也可用面积图来表示.
例1 在等差数列{an}中，
(1)已知a1＝，an＝－，Sn＝－5，求n和d；
(2)已知a1＝4，S8＝172，求a8和d；
(3)已知d＝2，an＝11，Sn＝35，求a1和n.
解：(1)由题意得，Sn＝＝＝－5，解得n＝15.
又∵a15＝＋(15－1)d＝－，
∴d＝－.
∴n＝15，d＝－.
(2)已知a1＝4，S8＝172，求a8和d；
(3)已知d＝2，an＝11，Sn＝35，求a1和n.
(2)由已知得S8＝＝＝172，解得a8＝39，
又∵a8＝4＋(8－1)d＝39，∴d＝5.
∴a8＝39，d＝5.
(3)∵an＝11，d＝2，Sn＝35，∴，
解得n＝5，a1＝3或n＝7，a1＝－1.
归纳总结
等差数列前n项和公式应用的关注点
例2 将数列{2n-1}与{3n-2}的公共项从小到大排列得到数列{an},则{an}的前n项和为________.
解析：由题意知数列{2n-1}为1,3,5,7,9,11,13,…,
{3n-2}为1,4,7,10,13,16,19,…,
∴数列{an}为1,7,13,19,…,即an=1+6(n-1)=6n-5,
∴数列{an}的前n项和为Sn==3n2-2n.
3n2-2n
1.已知数列{an}的通项公式为an=2-3n，n∈N+，则{an}的前n项和Sn等于( )
A.-n2+ B.-n2-
C.n2+ D.n2-
2.记等差数列的前n项和为Sn，若S2=4，S4=20，则该数列的公差d等于( )
A.2 B.3
C.6 D.7
A
B
3.在等差数列{an}中，若a3＋a5＋a7＋a9＋a11＝100，则3a9－a13的值为(　　)
A．20　　　　B．30 C．40 D．50
4.在等差数列{an}中，已知a1＝2，a9＝10，则S9等于(　　)
A.45　 B.52
C.108 D.54
C
D
根据今天所学，回答下列问题：
1.等差数列的前n项和公式是什么？
2.求等差数列的前n项和时两个公式该如何选择？
5.2.2 课时2
等差数列的前n项和的性质与应用
人教B版(2019)选择性必修第三册
1.掌握等差数列前n项和的性质及应用.
2.会求等差数列前n项和的最值.
3.能够求解与等差数列前n项和有关的实际应用题.
等差数列的前n项和公式
或
注意：两个公式都表明要求Sn必须已知n，a1，d，an中的三个.
等差数列的前n项和公式：n，
设A=，B=则=，
若A≠0(即d≠0)，则Sn是关于n的二次函数，即=的图象是抛物线y=上的一群孤立的点.
{an}是公差为2A的等差数列 =(A，B为常数)
若数列{an}是等差数列则=，
①当A=0，B=0(即d=0，a1=0)时，Sn=0是关于n的常数函数，{an}是各项为0的常数列；
②当A=0，B≠0(即d=0，a1≠0)时，Sn=Bn是关于n的正比例函数，{an}为各项非零的常数列；
③当A≠0(即d≠0)时， 是关于n的二次函数(常数项为0).
思考：数列{an}的前n项和=(A，B为常数)，则数列{an}是不是一定是等差数列？
=
从二次函数的角度看：
n
sn
a1＞0，d<0，有最大值
n
sn
a1＜0，d>0，有最小值
例1 已知等差数列{an}的前n项和为Sn，若a1＝10，公差d＝－2，Sn是否存在最大值？若存在，求Sn的最大值及取得最大值时n的值；若不存在，请说明理由.
解法1:由d＝－2，得an＋1－an＝－2＜0，得an＋1＜an ，所以{an}是递减数列.
由a1＝10，d＝－2，得an＝10＋(n－1)×(－2) ＝－2n＋12.
可知，当n＜6时，an＞0；当n＝6时，an＝0；当n＞6时，an＜0.
所以， S1＜S2＜…＜S5＝S6＞ S7＞…
也就是说，当n＝5或6时，Sn最大.
因为 =30，所以Sn的最大值为30.
解法2：∵由a1＝10，d＝－2，
∴，
所以，当n取与 最接近的整数，
即5或6时，Sn最大，最大值为30.
例1 已知等差数列{an}的前n项和为Sn，若a1＝10，公差d＝－2，Sn是否存在最大值？若存在，求Sn的最大值及取得最大值时n的值；若不存在，请说明理由.
解决等差数列前n项和的最值问题有两种方法：
(1) 当a1＞0，d＜0，前n项和有最大值.
可由an≥0，且an＋1 ≤0，求得n的值；
当a1＜0，d＞0，前n项和有最小值.
可由an≤0，且an＋1≥0，求得n的值.
(2) 由
利用二次函数配方法求得取最值时n的值.
总结归纳
讨论回答下列问题：
问题1：已知等差数列{an}的公差为d，前n项和为Sn，那么数列是什么
数列？
已知数列 的公差为 ，则 ，
所以有 ， .
因为 ，
所以数列 是首项为 ，公差为 的等差数列．
问题2：等差数列{an}中，你能发现其前n项和Sn、前2n项和S2n与前3n项和S3n有何关系吗？
S2n＝a1＋a2＋…＋an＋an＋1＋…＋a2n
＝Sn＋(a1＋nd)＋(a2＋nd)＋…＋(an＋nd)
＝2Sn＋n2d，
同样我们发现S3n＝3Sn＋3n2d，这里出现了一个有意思的数列
Sn，S2n－Sn＝Sn＋n2d，S3n－S2n＝Sn＋2n2d，…，
它是一个公差为n2d的等差数列.
问题3：an与S2n-1之间有什么等量关系？利用等差中项和等差数列求和公式进行推导.

问题4：公差为d，项数为2n项的等差数列{an}中，奇数项之和S奇与偶数项之和S偶有什么关系呢？若项数为(2n＋1)项呢？
若项数为 ，
则 ，
;
若项数为 ，由等差数列的性质可知， ，
所以 ,
，
所以 （这里 ， 是中间项），
．
等差数列{an}的前n项和Sn的性质
2.若Sm，S2m，S3m分别为公差是d的等差数列{an}的前m项、前2m项、前3m项的和，则Sm，S2m-Sm，S3m-S2m成公差是m2d的等差数列.
3.关于等差数列奇数项和与偶数项和的性质:
an是中间项
例2 项数为奇数的等差数列，奇数项之和为44，偶数项之和为33，求这个数列的中间项及项数.
解:设等差数列{an}共有(2n＋1)项，则奇数项有(n＋1)个，偶数项有n个，中间项是第(n＋1)项，即an＋1，
又因为S奇＝(n＋1)·an＋1＝44，
故这个数列的中间项为11，共有2n＋1＝7(项).
所以an＋1＝11.
解：植树工人每种一棵树并返回A处所要走的路程（单位：m）组成了一个数列 0，20，40，60，…，380，
例3 在新城大道一侧A处，运来20棵新树苗.一名工人从A处起沿大道一侧路边每隔10 m栽一棵树苗，这名工人每次只能运一棵.要栽完这20棵树苗，并返回A处，植树工人共走了多少路程？
这是首项a1 = 0，公差d=20，项数n=20的等差数列，其和
因此，植树工人共走了3 800m的路程.
1.在等差数列{an}中，若S10＝120，则a1＋a10的值是(　　)
A.12 B.24 C.36 D.48
2.已知等差数列{an}的前n项和为Sn，7a5+5a9=0，且a9>a5，则Sn取得最小值时n的值为(　　)
A.5 B.6 C.7 D.8
B
B
3.中国古诗词中，有一道“八子分绵”的数学名题：“九百九十六斤绵，赠分八子作盘缠，次第每人多十七，要将第八数来言”．题意是：把996斤绵分给8个儿子作盘缠，按照年龄从大到小的顺序依次分绵，年龄小的比年龄大的多17斤绵，那么第8个儿子分到的绵是(　　)
A．201斤　　 B．191斤　　 C．184斤　　 D．174斤
C
根据今天所学，回答下列问题：
1.数列中an与Sn的关系是什么？
2.等差数列前 n 项和的性质有哪些？
3.如何利用等差数列的通项公式与前 n 项和公式求Sn 的最值.