人教版九年级数学上册 25.2 用例举法求概率 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学上册 25.2 用例举法求概率 课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 15:43:28 | ||
图片预览



文档简介
九年级数学上册新人教版第二十五章第2节《用例举法求概率》课时练习
一、单选题
1.在一个不透明的袋中装着2个红球和1个白球,它们只有颜色上的区别,随机从袋中摸出一个小球,记下颜色后放回,再随机的取出一个球,两次恰好是一个红球和一个白球的概率为( )
A. B. C. D.
2.某中学初三年级四个班,四个数学老师分别任教不同的班.期末考试时,学校安排统一监考,要求同年级数学老师交换监考,那么安排初三年级数学考试时可选择的监考方案有( )种.
A.8 B.9 C.10 D.12
3.2023年被确定为“消费提振年”,将分别写有“消”“费”“提”“振”“年”这五个汉字的卡片放进不透明的盒子里,这些卡片除了汉字不同外,其他完全相同,现从盒子里摸出一张卡片不放回,再摸出另外一张,则两张卡片上的字恰好能组成“提振”一词的概率是( )
A. B. C. D.
4.转动A、B两个盘当指针分别指向红色和蓝色时称为配紫色成功.如图转动A、B各一次配紫色成功的概率是( )
A. B. C. D.
5.甲袋中装着分别标有数字2,,,的同质同大小的四个球,乙袋中装着分别标有运算符号“”、“”的同质同大小的两个球,先从甲袋中任意摸出两球,再从乙袋中摸出一球,让甲袋中摸出的两球上标的数按乙袋摸出球的运算符号计算,则结果是有理数的概率为( )
A. B. C. D.
6.《宋人扑枣图轴》是创作于宋朝的古画,该作品描绘了古人扑枣的场景.院角枣树果实累累,小孩群来攀扯,有的牵起衣角,有的捧着盘子拾取,一片兴高采烈之情跃然于绢帛之上.在某晚会上,某剧团准备根据该图编排一个舞蹈,舞蹈中甲乙两人分别模仿图中小孩扑枣的攀、牵、捧、拾中的一个动作(甲乙模仿的动作不同),他俩模仿的动作恰好是“攀”和“牵”的概率是( )
A. B. C. D.
7.在践行“安全在我心中,你我一起行动”主题手抄报评比活动中,共设置“交通安全、消防安全、饮食安全、防疫安全”四个主题内容,推荐两名学生参加评比,若他们每人从以上四个主题内容中随机选取一个,则两人恰好选中同一主题的概率是( )
A. B. C. D.
8.语文课上,同学们以“并州犹是诗故乡——唐代山西诗人群像”为主题展开研习活动.小彬和小颖计划从王维、柳宗元、白居易、王勃四位唐代山西诗人中任选一位撰写研习报告,则他们恰好选择的是同一位诗人的概率是( )
A. B. C. D.
二、填空题
9.已知一个不透明的盒子里装有5个只有颜色不同的球,其中3个红球,2个白球.从中任意摸出两个球,则摸出两球颜色相同的概率是 .
10.在三行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),开始时,骰子如图所示摆放,朝上的点数是2,最后翻动到如图所示位置,若要求翻动次数最少,则最后骰子朝上的点数为2的概率是
11.现有、两枚均匀的小立方体(立方体的每个面上分别标有数字、、、、、).用小明掷立方体朝上的数字为,小明掷立方体朝上的数字为来确定点,则小明各掷一次所确定的点落在已知抛物线上的概率是 .
12.现将背面完全相同,正面分别标有数、1、2、3的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为,再从剩下的3张卡片中任取一张,将该卡片上的数记为,则数字、中只有一个是方程的解的概率为 .
13.一个不透明的袋中装有四张形状大小质地完全相同的卡片,它们上画分别标有数字0,1,2,3,随机抽取一张不放回,再随机抽取一张,两次抽取的卡片数字同奇偶的概率是 .
14.重庆是餐饮文化名城,特别是重庆火锅以麻、辣、鲜、香的味道传遍大江南北、某游客慕名而来,决定从“德庄老火锅”“周师兄大刀腰片火锅”“卤校长老火锅”“白象街火锅”这个品牌的火锅中随机选取个进行品尝,则他抽到“德庄老火锅”和“卤校长老火锅”的概率为 .
15.从3,0,-1,-2,-3这五个数中.随机抽取一个数,作为函数和关于x的方程中m的值,恰好使函数的图象经过第一、三象限,且方程有实数根的概率是 .
16.甲、乙是两个不透明的纸箱,甲中有三张标有数字,1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b.若a,b能使关于x的一元二次方程有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为 .
三、解答题
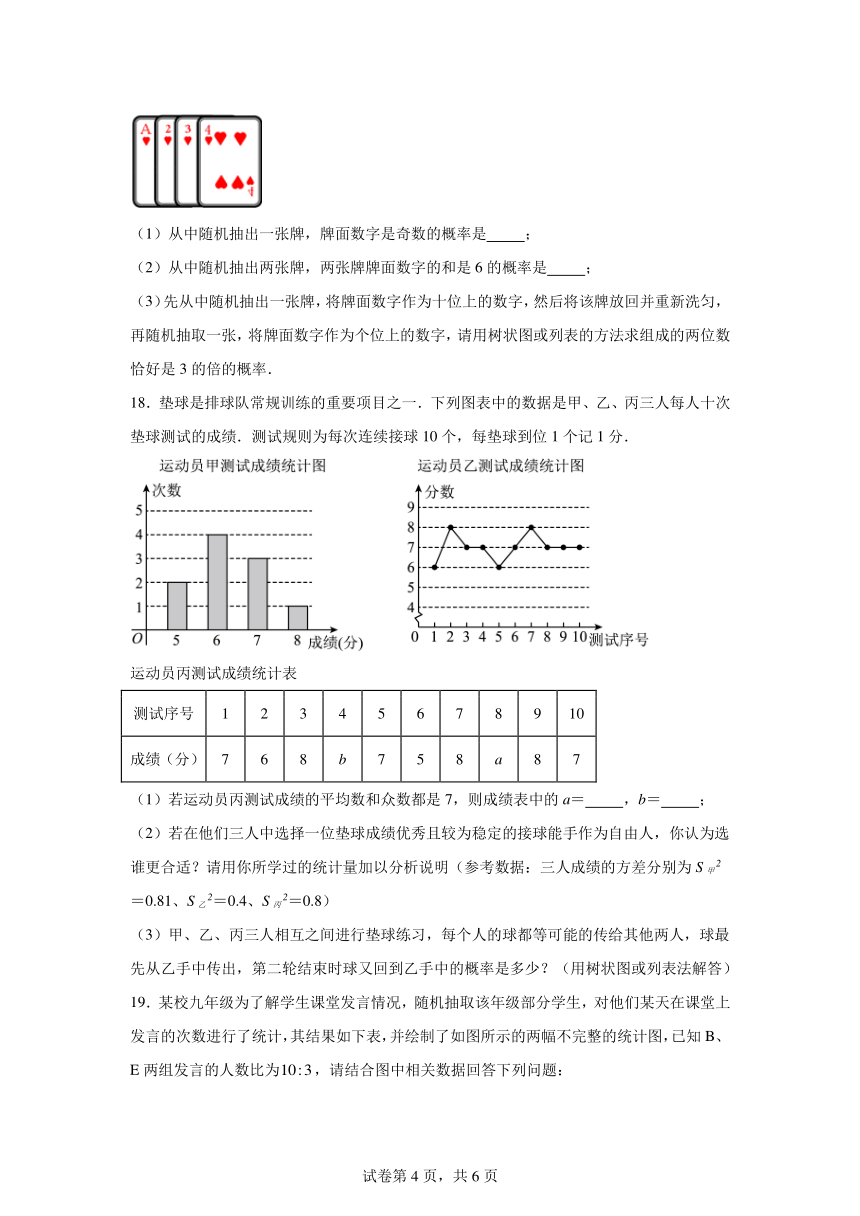
17.将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是奇数的概率是 ;
(2)从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率.
18.垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
运动员丙测试成绩统计表
测试序号 1 2 3 4 5 6 7 8 9 10
成绩(分) 7 6 8 b 7 5 8 a 8 7
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩表中的a= ,b= ;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为S甲2=0.81、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,第二轮结束时球又回到乙手中的概率是多少?(用树状图或列表法解答)
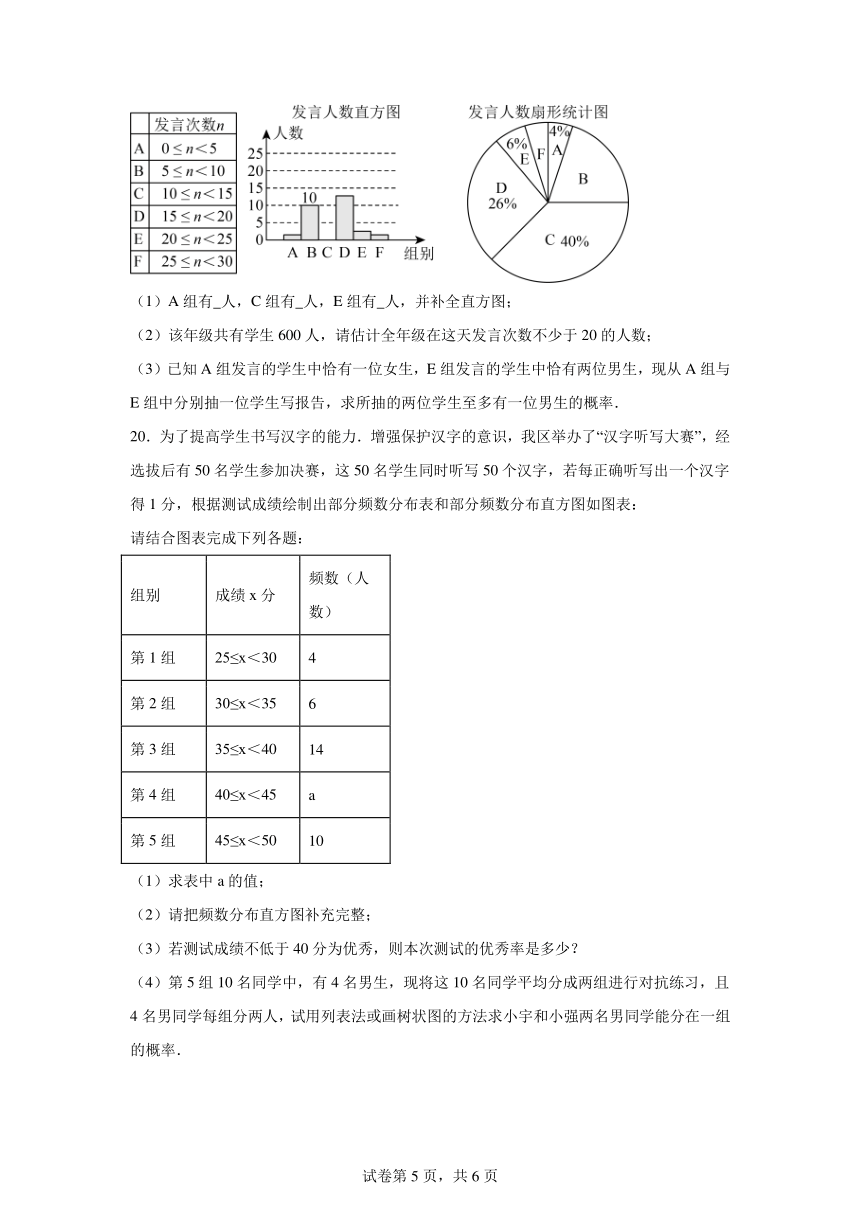
19.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言的人数比为,请结合图中相关数据回答下列问题:
(1)A组有 人,C组有 人,E组有 人,并补全直方图;
(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;
(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.
20.为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
组别 成绩x分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 6
第3组 35≤x<40 14
第4组 40≤x<45 a
第5组 45≤x<50 10
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男生,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,试用列表法或画树状图的方法求小宇和小强两名男同学能分在一组的概率.
21.我校计划成立学生体育社团,为了解学生对不同体育项目的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个体育项目”问卷调查,规定每人必须并且只能在“篮球”“足球”“乒乓球”“健美操”“跑步”五个项目中选择一项,并根据统计结果绘制了两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该校一共抽样调查了______ 名学生,扇形统计图中“跑步”项目所对应的扇形圆心角的度数是______ ;请补全条形统计图;
(2)若该校共有1200名学生,试估计该校学生中最喜爱“篮球”项目的人数;
(3)若随机从“篮球、足球、乒乓球”三项中抽取两个项目成立球类体育社团,其中“篮球”被选中的概率是多少?请用画树状图或列表等方法说明理由
试卷第1页,共3页
试卷第1页,共3页
《七年级数学下册新人教版第二十五章第2节《用例举法求概率》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 B B B A B C D A
9./0.4
10.
11.
12.
13..
14.
15.
16.解:关于x的一元二次方程有两个不相等的实数根,
∴,即,
画树状图表示所有等可能结果如下,抽取结果表示为,
共有9种等可能结果,其中的有,,,,,共5种,
∴甲获胜的概率为,则乙获胜的概率为,
故答案为: .
17.解:(1)1,2,3,4共有4张牌,随意抽取一张为偶数的概率为 =;
(2)只有2+4=6,但组合一共有3+2+1=6,故概率为;
(3)列表如下:
第二次 第一次 1 2 3 4
1 11 12 13 14
2 21 22 23 24
3 31 32 33 34
4 41 42 43 44
其中恰好是3的倍数的有12,21,24,33,42五种结果.
所以,P(3的倍数)=.
故答案为,.
18.解:(1)由众数的意义可知,a、b中至少有一个为7,又平均数是7,即(56+a+b)÷10=7,
因此,a=7,b=7,
故答案为:7,7;
(2)甲的平均数为:==6.3分,众数是6分,
乙的平均数为: ==7分,众数为7分,
丙的平均数为:=7分,众数为7分,
从平均数上看,乙、丙的较高,从众数上看乙、丙较高,
但S乙2=0.4<S丙2=0.8,
因此,综合考虑,选乙更合适.
(3)树状图如图所示:
∴第二轮结束时球又回到乙手中的概率P=.
19.解:(1)∵B、E两组发言的人数比为,E组发言人数的百分比为,
∴B组发言人数的百分比为
∴发言的人数人
∴A组有人,C组有人,E组有人
(2)由题意得(人)
答:全年级在这天发言次数不少于20的人数为60人;
(3)列树状图:
共有6六种等可能情况,符合至多有一位男生的情况有4种
因此(至多有一位男生).
20.解:(1)a=50﹣4﹣6﹣14﹣10=16.
(2)频数分布直方图如图所示:
(3)优秀率=×100%=52%.
(4)用A表示小宇、B表示小强,C、D表示其他两名同学,
根据题意画树状图如下:
从上图可知共有12种等可能情况,小宇与小强两名男同学分在同一组的情况有4种,
则小宇与小强两名男同学分在同一组的概率是P=.
21.(1)解:调查的总人数为名,
扇形统计图中“跑步”项目所对应的扇形圆心角的度数为,
选择“足球”的人数为名,
补全条形统计图为:
故答案为:200,72;
(2)解:(名),
所以估计该校学生中最喜爱“篮球”项目的人数为180名;
(3)解:画树状图为:
共有6种等可能的结果,其中抽取两个项目中至少一项是“篮球”的结果数为4,
所以抽取两个项目中至少一项是“篮球”的概率为:.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在一个不透明的袋中装着2个红球和1个白球,它们只有颜色上的区别,随机从袋中摸出一个小球,记下颜色后放回,再随机的取出一个球,两次恰好是一个红球和一个白球的概率为( )
A. B. C. D.
2.某中学初三年级四个班,四个数学老师分别任教不同的班.期末考试时,学校安排统一监考,要求同年级数学老师交换监考,那么安排初三年级数学考试时可选择的监考方案有( )种.
A.8 B.9 C.10 D.12
3.2023年被确定为“消费提振年”,将分别写有“消”“费”“提”“振”“年”这五个汉字的卡片放进不透明的盒子里,这些卡片除了汉字不同外,其他完全相同,现从盒子里摸出一张卡片不放回,再摸出另外一张,则两张卡片上的字恰好能组成“提振”一词的概率是( )
A. B. C. D.
4.转动A、B两个盘当指针分别指向红色和蓝色时称为配紫色成功.如图转动A、B各一次配紫色成功的概率是( )
A. B. C. D.
5.甲袋中装着分别标有数字2,,,的同质同大小的四个球,乙袋中装着分别标有运算符号“”、“”的同质同大小的两个球,先从甲袋中任意摸出两球,再从乙袋中摸出一球,让甲袋中摸出的两球上标的数按乙袋摸出球的运算符号计算,则结果是有理数的概率为( )
A. B. C. D.
6.《宋人扑枣图轴》是创作于宋朝的古画,该作品描绘了古人扑枣的场景.院角枣树果实累累,小孩群来攀扯,有的牵起衣角,有的捧着盘子拾取,一片兴高采烈之情跃然于绢帛之上.在某晚会上,某剧团准备根据该图编排一个舞蹈,舞蹈中甲乙两人分别模仿图中小孩扑枣的攀、牵、捧、拾中的一个动作(甲乙模仿的动作不同),他俩模仿的动作恰好是“攀”和“牵”的概率是( )
A. B. C. D.
7.在践行“安全在我心中,你我一起行动”主题手抄报评比活动中,共设置“交通安全、消防安全、饮食安全、防疫安全”四个主题内容,推荐两名学生参加评比,若他们每人从以上四个主题内容中随机选取一个,则两人恰好选中同一主题的概率是( )
A. B. C. D.
8.语文课上,同学们以“并州犹是诗故乡——唐代山西诗人群像”为主题展开研习活动.小彬和小颖计划从王维、柳宗元、白居易、王勃四位唐代山西诗人中任选一位撰写研习报告,则他们恰好选择的是同一位诗人的概率是( )
A. B. C. D.
二、填空题
9.已知一个不透明的盒子里装有5个只有颜色不同的球,其中3个红球,2个白球.从中任意摸出两个球,则摸出两球颜色相同的概率是 .
10.在三行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),开始时,骰子如图所示摆放,朝上的点数是2,最后翻动到如图所示位置,若要求翻动次数最少,则最后骰子朝上的点数为2的概率是
11.现有、两枚均匀的小立方体(立方体的每个面上分别标有数字、、、、、).用小明掷立方体朝上的数字为,小明掷立方体朝上的数字为来确定点,则小明各掷一次所确定的点落在已知抛物线上的概率是 .
12.现将背面完全相同,正面分别标有数、1、2、3的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为,再从剩下的3张卡片中任取一张,将该卡片上的数记为,则数字、中只有一个是方程的解的概率为 .
13.一个不透明的袋中装有四张形状大小质地完全相同的卡片,它们上画分别标有数字0,1,2,3,随机抽取一张不放回,再随机抽取一张,两次抽取的卡片数字同奇偶的概率是 .
14.重庆是餐饮文化名城,特别是重庆火锅以麻、辣、鲜、香的味道传遍大江南北、某游客慕名而来,决定从“德庄老火锅”“周师兄大刀腰片火锅”“卤校长老火锅”“白象街火锅”这个品牌的火锅中随机选取个进行品尝,则他抽到“德庄老火锅”和“卤校长老火锅”的概率为 .
15.从3,0,-1,-2,-3这五个数中.随机抽取一个数,作为函数和关于x的方程中m的值,恰好使函数的图象经过第一、三象限,且方程有实数根的概率是 .
16.甲、乙是两个不透明的纸箱,甲中有三张标有数字,1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b.若a,b能使关于x的一元二次方程有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为 .
三、解答题
17.将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是奇数的概率是 ;
(2)从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率.
18.垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
运动员丙测试成绩统计表
测试序号 1 2 3 4 5 6 7 8 9 10
成绩(分) 7 6 8 b 7 5 8 a 8 7
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩表中的a= ,b= ;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为S甲2=0.81、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,第二轮结束时球又回到乙手中的概率是多少?(用树状图或列表法解答)
19.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言的人数比为,请结合图中相关数据回答下列问题:
(1)A组有 人,C组有 人,E组有 人,并补全直方图;
(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;
(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.
20.为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
组别 成绩x分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 6
第3组 35≤x<40 14
第4组 40≤x<45 a
第5组 45≤x<50 10
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男生,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,试用列表法或画树状图的方法求小宇和小强两名男同学能分在一组的概率.
21.我校计划成立学生体育社团,为了解学生对不同体育项目的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个体育项目”问卷调查,规定每人必须并且只能在“篮球”“足球”“乒乓球”“健美操”“跑步”五个项目中选择一项,并根据统计结果绘制了两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该校一共抽样调查了______ 名学生,扇形统计图中“跑步”项目所对应的扇形圆心角的度数是______ ;请补全条形统计图;
(2)若该校共有1200名学生,试估计该校学生中最喜爱“篮球”项目的人数;
(3)若随机从“篮球、足球、乒乓球”三项中抽取两个项目成立球类体育社团,其中“篮球”被选中的概率是多少?请用画树状图或列表等方法说明理由
试卷第1页,共3页
试卷第1页,共3页
《七年级数学下册新人教版第二十五章第2节《用例举法求概率》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 B B B A B C D A
9./0.4
10.
11.
12.
13..
14.
15.
16.解:关于x的一元二次方程有两个不相等的实数根,
∴,即,
画树状图表示所有等可能结果如下,抽取结果表示为,
共有9种等可能结果,其中的有,,,,,共5种,
∴甲获胜的概率为,则乙获胜的概率为,
故答案为: .
17.解:(1)1,2,3,4共有4张牌,随意抽取一张为偶数的概率为 =;
(2)只有2+4=6,但组合一共有3+2+1=6,故概率为;
(3)列表如下:
第二次 第一次 1 2 3 4
1 11 12 13 14
2 21 22 23 24
3 31 32 33 34
4 41 42 43 44
其中恰好是3的倍数的有12,21,24,33,42五种结果.
所以,P(3的倍数)=.
故答案为,.
18.解:(1)由众数的意义可知,a、b中至少有一个为7,又平均数是7,即(56+a+b)÷10=7,
因此,a=7,b=7,
故答案为:7,7;
(2)甲的平均数为:==6.3分,众数是6分,
乙的平均数为: ==7分,众数为7分,
丙的平均数为:=7分,众数为7分,
从平均数上看,乙、丙的较高,从众数上看乙、丙较高,
但S乙2=0.4<S丙2=0.8,
因此,综合考虑,选乙更合适.
(3)树状图如图所示:
∴第二轮结束时球又回到乙手中的概率P=.
19.解:(1)∵B、E两组发言的人数比为,E组发言人数的百分比为,
∴B组发言人数的百分比为
∴发言的人数人
∴A组有人,C组有人,E组有人
(2)由题意得(人)
答:全年级在这天发言次数不少于20的人数为60人;
(3)列树状图:
共有6六种等可能情况,符合至多有一位男生的情况有4种
因此(至多有一位男生).
20.解:(1)a=50﹣4﹣6﹣14﹣10=16.
(2)频数分布直方图如图所示:
(3)优秀率=×100%=52%.
(4)用A表示小宇、B表示小强,C、D表示其他两名同学,
根据题意画树状图如下:
从上图可知共有12种等可能情况,小宇与小强两名男同学分在同一组的情况有4种,
则小宇与小强两名男同学分在同一组的概率是P=.
21.(1)解:调查的总人数为名,
扇形统计图中“跑步”项目所对应的扇形圆心角的度数为,
选择“足球”的人数为名,
补全条形统计图为:
故答案为:200,72;
(2)解:(名),
所以估计该校学生中最喜爱“篮球”项目的人数为180名;
(3)解:画树状图为:
共有6种等可能的结果,其中抽取两个项目中至少一项是“篮球”的结果数为4,
所以抽取两个项目中至少一项是“篮球”的概率为:.
答案第1页,共2页
答案第1页,共2页
同课章节目录
