2025年浙江省中考数学一轮复习专题检测 专题29 尺规作图与定义、命题、定理(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题29 尺规作图与定义、命题、定理(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 16:22:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题29 尺规作图与定义、命题、定理
一.选择题
1.(2024 恩施市模拟)下列语句中,不是命题的是( )
A.两直线平行,同旁内角相等 B.若2a=4,则a=2
C.过一点作已知直线的平行线 D.同角的余角相等
2.(2024 芙蓉区校级模拟)用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45° B.两个锐角都小于45°
C.两个锐角都不大于45° D.两个锐角都等于45°
3.(2024 北票市三模)下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x>y,则a2x>a2y.其中是真命题的是( )
A.②③ B.①② C.①②④ D.①②③④
4.(2024 珠海校级一模)下列命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.如果两个实数相等,那么它们的平方相等
C.等边三角形是锐角三角形 D.如果两个实数的积是正数,那么它们都是正数
5.(2024 吴兴区二模)在平面直角坐标系中有A(a,b)与B(b,a)两点(a、b≠0),关于过A、B两点的直线l与二次函数y=ax2+bx+1图象的交点个数判定,哪项为真命题( )
A.如果b>0,那么一定有两交点 B.只有b<0,才一定有两交点
C.如果a<0,那么一定有两交点 D.只有a>0,才一定有两交点
6.(2024 平湖市模拟)用尺规作图作一个角的角平分线,下列作法错误的是( )
A. B. C. D.
7.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
8.(2024 眉山)如图,在△ABC中,AB=AC=6,BC=4,分别以点A,点B为圆心,大于的长为半径作弧,两弧交于点E,F,过点E,F作直线交AC于点D,连结BD,则△BCD的周长为( )
A.7 B.8 C.10 D.12
9.(2024 金东区二模)如图,在△ABC中,∠C=90°,用直尺和圆规在边BC上确定一点P,使点P到边AC、AB的距离相等,则符合要求的作图痕迹是( )
A. B. C. D.
10.(2024 普陀区二模)在△ABC中,只用无刻度直尺和圆规比较∠B与∠C的大小.除了“叠合法”外,嘉琪又想出两种方法:
方法一:作△ABC的高AD和角平分线AE,若E点在线段BD上,则说明∠B<∠C.
方法二:作BC边中垂线MN,若MN与AB边相交(不包括A点),则说明∠B<∠C.
下列说法正确的是( )
A.方法一可行,方法二不可行 B.方法二可行,方法一不可行
C.两种方法都可行 D.两种方法都不可行
11.(2024 龙湾区二模)如图,在△ABC中,分别以点A,B为圆心,大于为半径画弧,两弧交于点E,F,作直线EF分别交BC,AB于点D,M,连结AD.若AC=4,CD=3,AD=5,则AB的长为( )
A. B. C.9 D.10
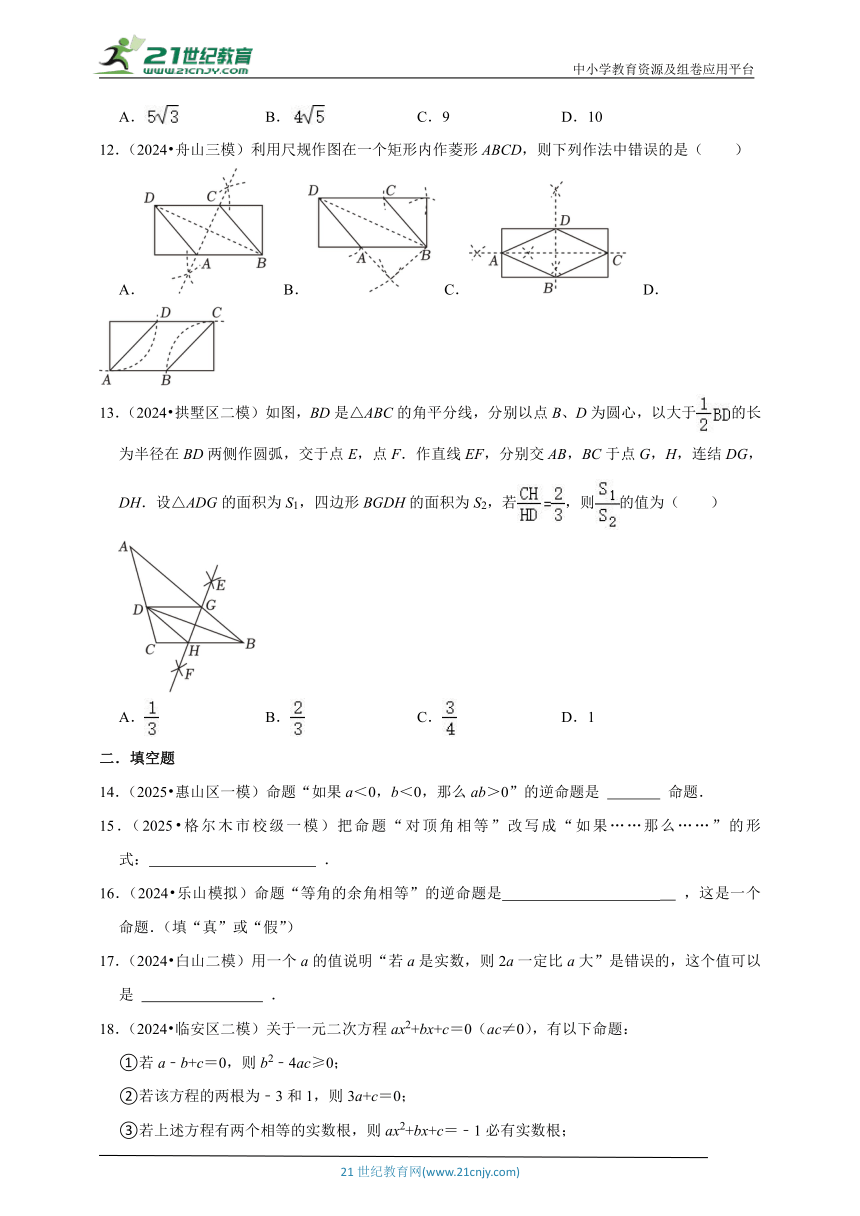
12.(2024 舟山三模)利用尺规作图在一个矩形内作菱形ABCD,则下列作法中错误的是( )
A. B. C. D.
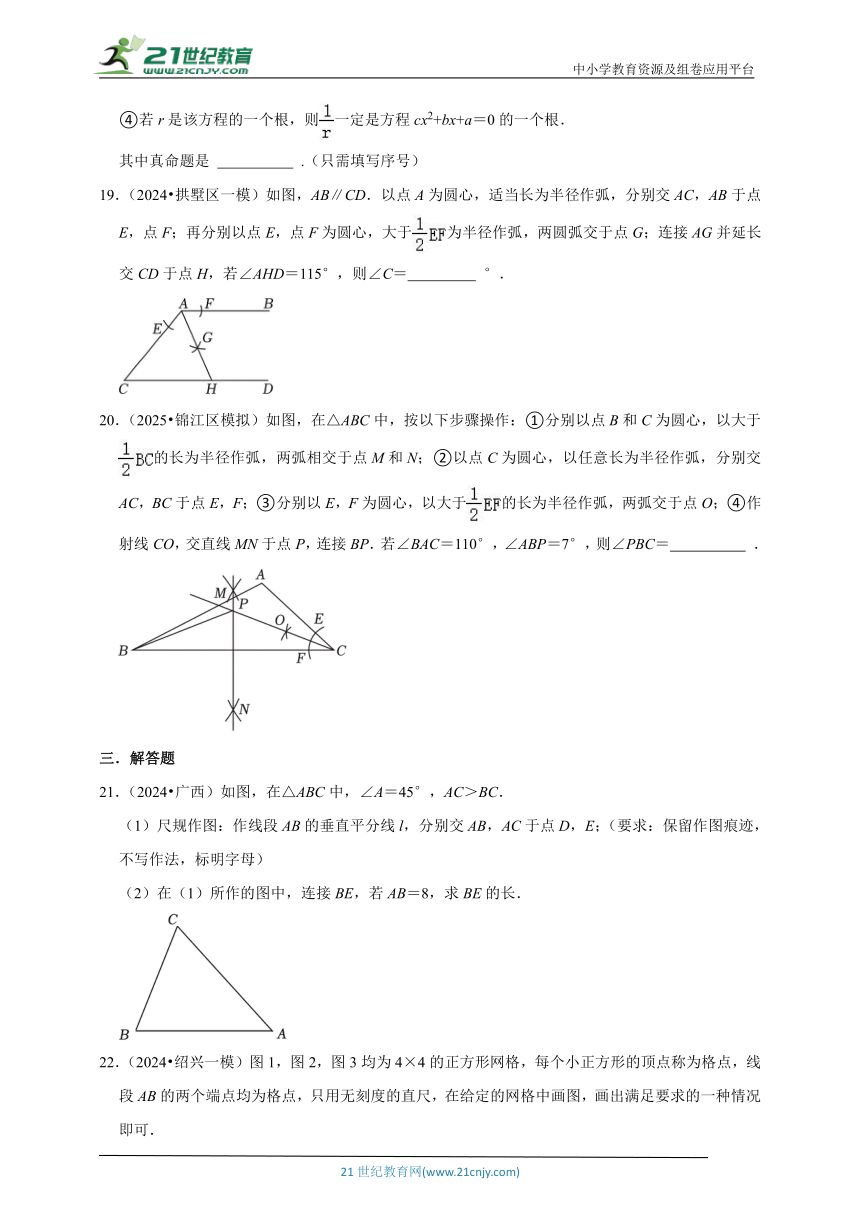
13.(2024 拱墅区二模)如图,BD是△ABC的角平分线,分别以点B、D为圆心,以大于的长为半径在BD两侧作圆弧,交于点E,点F.作直线EF,分别交AB,BC于点G,H,连结DG,DH.设△ADG的面积为S1,四边形BGDH的面积为S2,若,则的值为( )
A. B. C. D.1
二.填空题
14.(2025 惠山区一模)命题“如果a<0,b<0,那么ab>0”的逆命题是 命题.
15.(2025 格尔木市校级一模)把命题“对顶角相等”改写成“如果……那么……”的形式: .
16.(2024 乐山模拟)命题“等角的余角相等”的逆命题是 ,这是一个 命题.(填“真”或“假”)
17.(2024 白山二模)用一个a的值说明“若a是实数,则2a一定比a大”是错误的,这个值可以是 .
18.(2024 临安区二模)关于一元二次方程ax2+bx+c=0(ac≠0),有以下命题:
①若a﹣b+c=0,则b2﹣4ac≥0;
②若该方程的两根为﹣3和1,则3a+c=0;
③若上述方程有两个相等的实数根,则ax2+bx+c=﹣1必有实数根;
④若r是该方程的一个根,则一定是方程cx2+bx+a=0的一个根.
其中真命题是 .(只需填写序号)
19.(2024 拱墅区一模)如图,AB∥CD.以点A为圆心,适当长为半径作弧,分别交AC,AB于点E,点F;再分别以点E,点F为圆心,大于为半径作弧,两圆弧交于点G;连接AG并延长交CD于点H,若∠AHD=115°,则∠C= °.
20.(2025 锦江区模拟)如图,在△ABC中,按以下步骤操作:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②以点C为圆心,以任意长为半径作弧,分别交AC,BC于点E,F;③分别以E,F为圆心,以大于的长为半径作弧,两弧交于点O;④作射线CO,交直线MN于点P,连接BP.若∠BAC=110°,∠ABP=7°,则∠PBC= .
三.解答题
21.(2024 广西)如图,在△ABC中,∠A=45°,AC>BC.
(1)尺规作图:作线段AB的垂直平分线l,分别交AB,AC于点D,E;(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接BE,若AB=8,求BE的长.
22.(2024 绍兴一模)图1,图2,图3均为4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的两个端点均为格点,只用无刻度的直尺,在给定的网格中画图,画出满足要求的一种情况即可.
(1)在图1中找一个格点P,连结BP,使∠ABP=45°.
(2)在图2中找两个格点P,Q,连结PQ,使直线PQ⊥AB.
(3)在图3中找两个格点P,Q,连结PQ交线段AB于点C,使AC=3BC.
23.(2024 普陀区二模)已知平行四边形ABCD,观察如图所示的尺规作图痕迹.
(1)求证:四边形ABEF是菱形;
(2)连结AE,若AE=6,BF=8,求菱形ABEF的周长.
24.(2024 定海区三模)阅读理解:
我们解决某些数学题的时候,经常会遇到题目中的条件比较含糊,它们常常巧妙地隐蔽在题设的背后,不易被发现和运用,导致我们解题受阻,因此,挖掘题设中的隐含条件,应该成为我们必备的一种能力.请阅读下面的解题过程,体会如何发现隐含条件,并依次解决所给的问题.
化简:.
解:由题意可知隐含条件1﹣5a≥0,解得:,
∴1﹣a>0,
∴.
启发应用:
(1)按照上面的解法,化简:;
类比迁移:
(2)已知△ABC的三边长分别为,,,请求出△ABC的周长.(用含有x、y的代数式表示,结果要求化简)
拓展延伸:
(3)若,请直接写出x的取值范围.
答案与解析
一.选择题
1.(2024 恩施市模拟)下列语句中,不是命题的是( )
A.两直线平行,同旁内角相等 B.若2a=4,则a=2
C.过一点作已知直线的平行线 D.同角的余角相等
【点拨】根据命题的定义作答.
【解析】解:根据命题的定义,可知A、B、D都是命题,
而C属于作图语言,不是命题.
故选:C.
【点睛】本题考查了命题的定义:一般的,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.一般说来,对于任何一个命题,都可以加上“是”或“不是”.注意,作图语言不是命题.
2.(2024 芙蓉区校级模拟)用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45° B.两个锐角都小于45°
C.两个锐角都不大于45° D.两个锐角都等于45°
【点拨】用反证法证明命题的真假,应先按符合题设的条件,假设题设成立,再判断得出的结论是否成立即可.
【解析】解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,
应先假设两个锐角都大于45°.
故选:A.
【点睛】本题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
3.(2024 北票市三模)下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x>y,则a2x>a2y.其中是真命题的是( )
A.②③ B.①② C.①②④ D.①②③④
【点拨】根据对顶角相等,平行线的判定,等式的性质,不等式的性质,逐一进行判断即可.
【解析】解:对顶角相等,故①为真命题;
同位角相等,两直线平行,故②为真命题;
若|a|=|b|,则a=b或a=﹣b,故③为假命题;
若x>y,当a≠0时,则a2x>a2y,故④为假命题.
故选:B.
【点睛】本题考查命题的真假,正确记忆相关知识点是解题关键.
4.(2024 珠海校级一模)下列命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.如果两个实数相等,那么它们的平方相等
C.等边三角形是锐角三角形 D.如果两个实数的积是正数,那么它们都是正数
【点拨】利用全等三角形的性质、实数的性质、等边三角形的性质等知识分别判断后即可确定正确的选项.
【解析】解:A、逆命题为对应角相等的三角形全等,不成立,不符合题意;
B、逆命题为如果两个数的平方相等,那么这两个数相等,不成立,不符合题意;
C、逆命题为锐角三角形是等边三角形,不成立,不符合题意;
D、逆命题为如果两个数都是正数,那么它们的积也是正数,成立,符合题意.
故选:D.
【点睛】考查了命题与定理,解题的关键是了解如何写出一个命题的逆命题,难度不大.
5.(2024 吴兴区二模)在平面直角坐标系中有A(a,b)与B(b,a)两点(a、b≠0),关于过A、B两点的直线l与二次函数y=ax2+bx+1图象的交点个数判定,哪项为真命题( )
A.如果b>0,那么一定有两交点 B.只有b<0,才一定有两交点
C.如果a<0,那么一定有两交点 D.只有a>0,才一定有两交点
【点拨】根据点A和点B的坐标,求出直线l的表达式,联立直线l与二次函数表达式,根据根的判别式求出一定有两个交点时必须满足条件b>0或a<0,然后分a+b=1和a+b≠1两种情况进行解答即可.
【解析】解:设直线l的表达式为:y=kx+m,
将点A,B的坐标代入表达式得:
,
解得:k=﹣1,m=a+b,
∴直线l的表达式为:y=﹣x+a+b,
联立二次函数表达式得:
﹣x+a+b=ax2+bx+1,
整理得:ax2+(b+1)x+1﹣a﹣b=0,
∴Δ=(b+1)2﹣4a(1﹣a﹣b)=4a2+4ab+b2﹣4a+2b+1=(2a+b﹣1)2+4b=(b+2a+1)2﹣8a,
要使Δ>0恒成立,∴b>0或a<0,
又二次函数y=ax2+bx+1的图象与y轴的交点坐标为(0,1),直线l:y=﹣x+a+b与y轴的交点坐标为(0,a+b),
∴当a+b≠1时,满足条件b>0或a<0,则直线l与二次函数y=ax2+bx+1的图象一定有两个交点,
当a+b=1时,直线l与二次函数y=ax2+bx+1的图象一定有一个定交点(0,1),
∵a+b=1,∴b=1﹣a,当a>0时,b<1,当a<0时,b>1,
若a<0,b>1,则直线l与二次函数y=ax2+bx+1的图象一定有两个交点,
若a>0,b<1,此时必须满足条件0<b<1,直线l与二次函数y=ax2+bx+1的图象才一定有两个交点,
若此时b<0,则直线l与二次函数y=ax2+bx+1的图象只有一个交点,即为(0,1),
∴只有a<0,才一定有两交点.
故选:C.
【点睛】本题考查了一次函数与二次函数的交点问题,熟练掌握根的判别式是解题的基础,确定a+b=1时的取值情况是解题的关键和难点.
6.(2024 平湖市模拟)用尺规作图作一个角的角平分线,下列作法错误的是( )
A. B. C. D.
【点拨】根据各个选项中的作图,可以判断哪个选项符合题意.
【解析】解:A.如图,
由作图可知,OA=OC,AB=BC,
又∵OB=OB,
∴△OAB≌△OCB(SSS),
∴∠AOB=∠COB,
∴OB平分∠AOC,
故选项A是在作角平分线,不符合题意;
B.如图,
由作图得,∠AOB=∠MBC,BO=BC,
∴BCAO,∠BOC=∠BCO,
∴∠AOC=∠BCO,
∴∠AOC=∠BOC,
∴OC 平分∠AOB,
故选项B是在作角平分线,不符合题意;
C.如图,
由作图知,点P是的中点,
∴,
∴∠NAP=∠MAP,
∴AP平分∠MAN,
故选项C是在作角平分线,不符合题意;
D.如图,
由作图知,AC与AB不一定相等,CP=BP,AP=AP,
∴△ACP与△ABP不全等,
∴∠CAP≠∠BAP,
∴AP不平分∠BAC,
∴AP 不是∠BAC 的平分线,
故选:D.
【点睛】本题考查作图—基本作图,解答本题的关键是明确角平分线的做法,利用数形结合的思想解答.
7.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
【点拨】由直角三角形两锐角互余可求出∠BAC=50°,由作图得∠BAD=25°,由三角形的外角的性质可得∠ADC=65°,故可得答案.
【解析】解:∵∠C=90°,∠B=40°,
∴∠BAC=90°﹣∠B=90°﹣40°=50°,
由作图知,AP平分∠BAC,
∴,
∵∠ADC=∠B+∠BAD,
∴∠ADC=40°+25°=65°,
故选:B.
【点睛】本题主要考查基本作图,直角三角形两锐角互余以及三角形外角的性质,掌握尺规作图的方法是解题的关键.
8.(2024 眉山)如图,在△ABC中,AB=AC=6,BC=4,分别以点A,点B为圆心,大于的长为半径作弧,两弧交于点E,F,过点E,F作直线交AC于点D,连结BD,则△BCD的周长为( )
A.7 B.8 C.10 D.12
【点拨】根据线段垂直平分线的性质得到AD=BD,根据三角形的周长公式即可得到结论.
【解析】解:由作图知,EF垂直平分AB,
∴AD=BD,
∴△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC,
∵AB=AC=6,BC=4,
∴△BCD的周长=6+4=10,
故选:C.
【点睛】本题考查了作图﹣基本作图,线段垂直平分线的性质,三角形周长的计算,熟练掌握线段垂直平分线的性质是解题的关键.
9.(2024 金东区二模)如图,在△ABC中,∠C=90°,用直尺和圆规在边BC上确定一点P,使点P到边AC、AB的距离相等,则符合要求的作图痕迹是( )
A. B. C. D.
【点拨】P到边AC、AB的距离相等,可知点P在∠A的平分线上,由此判断即可.
【解析】解:∵P到边AC、AB的距离相等,
∴点P在∠A的平分线上.
故选:C.
【点睛】本题考查作图﹣复杂作图,角平分线的性质等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.
10.(2024 普陀区二模)在△ABC中,只用无刻度直尺和圆规比较∠B与∠C的大小.除了“叠合法”外,嘉琪又想出两种方法:
方法一:作△ABC的高AD和角平分线AE,若E点在线段BD上,则说明∠B<∠C.
方法二:作BC边中垂线MN,若MN与AB边相交(不包括A点),则说明∠B<∠C.
下列说法正确的是( )
A.方法一可行,方法二不可行 B.方法二可行,方法一不可行
C.两种方法都可行 D.两种方法都不可行
【点拨】分别画出图形,结合角平分线的定义、垂线的定义、线段垂直平分线的性质、三角形内角和定理进行判断即可得出答案.
【解析】解:方法一:如图1所示,
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∴∠CAD+∠C=90°,∠DAB+∠B=90°,
∵∠CAD=∠CAE﹣∠DAE,∠DAB=∠BAE+∠DAE,
∴∠C=90°﹣∠CAE+∠DAE,∠B=90°﹣∠BAE﹣∠DAE,
∴∠B<∠C;
∵点D与点E可能重合,线段包含端点,
∴方法一不可行;
方法二:如图2所示,
∵MN垂直平分BC,
∴CN=BN,
∴∠B=∠NCB,
∵∠C>∠NCB,
∴∠C>∠B;
综上所述,方法一不可行,方法二可行;
故选:B.
【点睛】本题考查了角平分线的定义、垂线的定义、线段垂直平分线的性质、三角形内角和定理,熟练掌握角平分线与垂线的定义是解答本题的关键.
11.(2024 龙湾区二模)如图,在△ABC中,分别以点A,B为圆心,大于为半径画弧,两弧交于点E,F,作直线EF分别交BC,AB于点D,M,连结AD.若AC=4,CD=3,AD=5,则AB的长为( )
A. B. C.9 D.10
【点拨】根据勾股定理得到逆定理得到∠C=90°,根据相似三角形的判定和性质定理即可得到结论.
【解析】解:由作图知,直线EF垂直平分AB,
∴AD=BD,DM⊥AB,BM=AM,
∵AC2+CD2=42+32=52=AD2,
∴∠C=90°,
∵∠BMD=∠C=90°,∠B=∠B,
∴△BDM∽△BCA,
∴,
∴,
∴AB=4,
故选:B.
【点睛】本题考查了作图﹣基本作图,线段垂直平分线的性质,相似三角形的判定和性质,勾股定理的逆定理,熟练掌握线段垂直平分线的性质是解题的关键.
12.(2024 舟山三模)利用尺规作图在一个矩形内作菱形ABCD,则下列作法中错误的是( )
A. B. C. D.
【点拨】根据菱形的判定和作图痕迹解答即可.
【解析】解:A、由作图可知,AC⊥BD,即对角线平分且垂直的四边形是菱形,正确;
B、由作图可知AD=DC,即邻边相等的平行四边形是菱形,正确;
C、由作图可知AC⊥BD,对角线平分且垂直的四边形是菱形,正确;
D、由作图可知∠DAC=∠CAB,∠DCA=∠ACB,对角线AC平分对角,可以得出是菱形,错误;
故选:D.
【点睛】本题考查作图﹣复杂作图,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.
13.(2024 拱墅区二模)如图,BD是△ABC的角平分线,分别以点B、D为圆心,以大于的长为半径在BD两侧作圆弧,交于点E,点F.作直线EF,分别交AB,BC于点G,H,连结DG,DH.设△ADG的面积为S1,四边形BGDH的面积为S2,若,则的值为( )
A. B. C. D.1
【点拨】先判断是菱形,再根据相似三角形的性质及比例的性质.
【解析】解:由作图得:EF垂直平分BD,
∴BG=DG,BH=DH,
∵BD是△ABC的角平分线,
∴BG=BH,
∴BG=DG=BH=DH,
∴四边形BHDG是菱形,
∴DG∥BC,DH∥AB,
∴△ADG∽△ACB,△CDH∽△CAB,
设CH=2a,△ABC的面积为S,△CDH的面积为S3,
则DH=DG=BH=3a,
∴S1=S,S3=S,
∴S2=S﹣S1﹣S3=S,
∴S1:S2=S:S=,
故选:C.
【点睛】本题考查了基本作图,掌握菱形的判定定理和性质、角平分线的性质,及相似三角形的性质是解题的关键.
二.填空题
14.(2025 惠山区一模)命题“如果a<0,b<0,那么ab>0”的逆命题是 假 命题.
【点拨】把一个命题的条件和结论互换就得到它的逆命题,进而利用举反例判断命题正确性即可.
【解析】解:“若a<0,b<0,则ab>0”的逆命题是“若ab>0,则a<0,b<0”,是一个假命题.
故答案为:假.
【点睛】本题考查命题与定理,正确写出原命题的逆命题是解题关键.
15.(2025 格尔木市校级一模)把命题“对顶角相等”改写成“如果……那么……”的形式: 如果两个角是对顶角,那么这两个角相等 .
【点拨】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面即可.
【解析】解:把命题“对顶角相等”改写成“如果 那么 ”的形式为:如果两个角是对顶角,那么这两个角相等.
故答案为:如果两个角是对顶角,那么这两个角相等.
【点睛】本题考查了把一个命题写成“如果 那么 ”的形式,命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.
16.(2024 乐山模拟)命题“等角的余角相等”的逆命题是 如果两个角的余角相等,那么这两个角也相等 ,这是一个 真 命题.(填“真”或“假”)
【点拨】先把等角的余角相等写成“如果…那么…”的形式,然后交换题设和结论即可得到逆命题,再判断其真假.
【解析】解:“等角的余角相等”的逆命题为“如果两个角的余角相等,那么这两个角也相等”,这是一个真命题.
故答案为如果两个角的余角相等,那么这两个角也相等;真.
【点睛】本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题.
17.(2024 白山二模)用一个a的值说明“若a是实数,则2a一定比a大”是错误的,这个值可以是 ﹣1(答案不唯一) .
【点拨】根据实数的大小比较法则解答即可.
【解析】解:当a=﹣1时,2a=﹣2,
则2a<a,
可以说明“若a是实数,则2a一定比a大”是错误的,
故答案为:﹣1(答案不唯一).
【点睛】本题考查的是反证法以及假命题的证明,要证明一个命题是真命题,需要严格的证明过程,而要证明一个命题是假命题,只需要举一个反例即可.
18.(2024 临安区二模)关于一元二次方程ax2+bx+c=0(ac≠0),有以下命题:
①若a﹣b+c=0,则b2﹣4ac≥0;
②若该方程的两根为﹣3和1,则3a+c=0;
③若上述方程有两个相等的实数根,则ax2+bx+c=﹣1必有实数根;
④若r是该方程的一个根,则一定是方程cx2+bx+a=0的一个根.
其中真命题是 ①②④ .(只需填写序号)
【点拨】由a﹣b+c=0得b=a+c,即得b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,判断①是真命题;由该方程的两根为﹣3和1得﹣3×1=,c=﹣3a,即得3a+c=0,判断②是真命题;由ax2+bx+c=0有两个相等的实数根知b2﹣4ac=0,而ax2+bx+c+1=0的判别式:b2﹣4a×(c+1)=b2﹣4ac+4a=﹣4a,因a的符号不确定,故方程ax2+bx+c=﹣1根的情况不确定,判断③是假命题;由r是该方程的一个根得ar2+br+c=0,又r≠0,即可得a+b +c ()2=0,是cx2+bx+a=0的一个根,判断④是真命题.
【解析】解:若a﹣b+c=0,则b=a+c,
∴b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,故①是真命题;
若该方程的两根为﹣3和1,则﹣3×1=,
∴c=﹣3a,
∴3a+c=0,故②是真命题;
若ax2+bx+c=0有两个相等的实数根,则b2﹣4ac=0,
∴ax2+bx+c+1=0的判别式:b2﹣4a×(c+1)=b2﹣4ac﹣4a=﹣4a,
∵a的符号不确定,
∴方程ax2+bx+c=﹣1根的情况不确定,故③是假命题;
若r是该方程的一个根,则ar2+br+c=0,
∵ac≠0,
∴r≠0,
∴=0,
∴a+b +c ()2=0,
∴是cx2+bx+a=0的一个根,故④是真命题;
∴真命题有:①②④;
故答案为:①②④.
【点睛】本题考查命题与定理,解题的关键是掌握一元二次方程根的判别式和根与系数的关系.
19.(2024 拱墅区一模)如图,AB∥CD.以点A为圆心,适当长为半径作弧,分别交AC,AB于点E,点F;再分别以点E,点F为圆心,大于为半径作弧,两圆弧交于点G;连接AG并延长交CD于点H,若∠AHD=115°,则∠C= 50 °.
【点拨】由作图过程可知,AH为∠BAC的平分线,则∠BAH=∠CAH,根据平行线的性质可得∠BAH=∠CAH=180°﹣115°=65°,再由三角形的外角性质可得∠C=∠AHD﹣∠CAH=50°.
【解析】解:由作图过程可知,AH为∠BAC的平分线,
∴∠BAH=∠CAH,
∵AB∥CD,∠AHD=115°,
∴∠BAH=180°﹣115°=65°,
∴∠CAH=65°,
∴∠C=∠AHD﹣∠CAH=50°.
故答案为:50.
【点睛】本题考查作图—基本作图、平行线的性质,熟练掌握平行线的性质、角平分线的作图方法是解答本题的关键.
20.(2025 锦江区模拟)如图,在△ABC中,按以下步骤操作:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②以点C为圆心,以任意长为半径作弧,分别交AC,BC于点E,F;③分别以E,F为圆心,以大于的长为半径作弧,两弧交于点O;④作射线CO,交直线MN于点P,连接BP.若∠BAC=110°,∠ABP=7°,则∠PBC= 21° .
【点拨】由作图过程可知,直线MN为线段BC的垂直平分线,CP为∠ACB的平分线,可得PB=PC,∠ACP=∠BCP,即∠PBC=∠BCP=∠ACP,结合三角形内角和定理可得∠BAC+∠ABP+∠PBC+∠BCP+∠ACP=180°,进而可得答案.
【解析】解:由作图过程可知,直线MN为线段BC的垂直平分线,CP为∠ACB的平分线,
∴PB=PC,∠ACP=∠BCP,
∴∠PBC=∠BCP=∠ACP.
∵∠BAC+∠ABC+∠ACB=180°,
即∠BAC+∠ABP+∠PBC+∠BCP+∠ACP=180°,
∴110°+7°+3∠PBC=180°,
∴∠PBC=21°.
故答案为:21°.
【点睛】本题考查作图—基本作图、线段垂直平分线的性质、角平分线的定义、三角形内角和定理,熟练掌握线段垂直平分线的性质、角平分线的定义、三角形内角和定理是解答本题的关键.
三.解答题
21.(2024 广西)如图,在△ABC中,∠A=45°,AC>BC.
(1)尺规作图:作线段AB的垂直平分线l,分别交AB,AC于点D,E;(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接BE,若AB=8,求BE的长.
【点拨】(1)根据要求作出图形;
(2)证明△BDE是等腰直角三角形,可得结论.
【解析】解:(1)图形如图所示:
(2)∵DE垂直平分线段AB,
∴EB=EA,
∴∠EBA=∠A=45°,
∴∠BEA=90°,
∵BD=DA,
∴DE=DB=DA=AB=4,
∴BE=BD=4.
【点睛】本题考查作图﹣基本作图,线段的垂直平分线,等腰直角三角形的性质等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.
22.(2024 绍兴一模)图1,图2,图3均为4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的两个端点均为格点,只用无刻度的直尺,在给定的网格中画图,画出满足要求的一种情况即可.
(1)在图1中找一个格点P,连结BP,使∠ABP=45°.
(2)在图2中找两个格点P,Q,连结PQ,使直线PQ⊥AB.
(3)在图3中找两个格点P,Q,连结PQ交线段AB于点C,使AC=3BC.
【点拨】(1)以AB为斜边作等腰直角三角形,直角顶点即为所求的格点P.
(2)结合垂直的定义利用网格画图即可.
(3)取格点P,Q,使AP=3BQ,且AP∥BQ,则P,Q即为所求.
【解析】解:(1)如图1,P'和P''均满足题意.
(2)如图2,P,Q即为所求(答案不唯一).
(3)如图3,取格点P,Q,使AP=3BQ,且AP∥BQ,
此时△APC∽△BQC,
∴AC:BC=AP:BQ=3:1,
即AC=3BC,
则P,Q即为所求.
【点睛】本题考查作图—应用与设计作图、等腰直角三角形的判定与性质、相似三角形的判定与性质,解题的关键是理解题意,灵活运用所学知识解决问题.
23.(2024 普陀区二模)已知平行四边形ABCD,观察如图所示的尺规作图痕迹.
(1)求证:四边形ABEF是菱形;
(2)连结AE,若AE=6,BF=8,求菱形ABEF的周长.
【点拨】(1)先证明四边形是平行四边形,再证明是菱形;
(2)先根据勾股定理求出边长,再求出周长.
【解析】(1)证明:设BF交AE于点O,
在平行四边形ABCD中,有AD∥BC,
∴∠AFB=∠FBE,
由作图得:BE=BA,BF平分∠ABC,
∴∠ABF=∠EBF,
∴∠ABF=∠AFB,
∴AF=AB,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴ ABEF为菱形;
(2)证明:∵ ABEF为菱形;
∴AO==3,BO==4,∠AOB=90°,
AB=BE=EF=AF,
∴AB==5,
∴菱形ABEF的周长为:4×5=20.
【点睛】本题考查了基本作图,掌握菱形的判定定理和性质定理和勾股定理是解题的关键.
24.(2024 定海区三模)阅读理解:
我们解决某些数学题的时候,经常会遇到题目中的条件比较含糊,它们常常巧妙地隐蔽在题设的背后,不易被发现和运用,导致我们解题受阻,因此,挖掘题设中的隐含条件,应该成为我们必备的一种能力.请阅读下面的解题过程,体会如何发现隐含条件,并依次解决所给的问题.
化简:.
解:由题意可知隐含条件1﹣5a≥0,解得:,
∴1﹣a>0,
∴.
启发应用:
(1)按照上面的解法,化简:;
类比迁移:
(2)已知△ABC的三边长分别为,,,请求出△ABC的周长.(用含有x、y的代数式表示,结果要求化简)
拓展延伸:
(3)若,请直接写出x的取值范围.
【点拨】(1)先根据二次根式有意义的条件求出m的范围,再根据二次根式的性质化简即可;
(2)先根据二次根式有意义的条件求出x、y的范围,再根据二次根式的性质化简即可;
(3)先根据二次根式有意义的条件求出x的范围,再分类讨论,根据二次根式的性质化简即可.
【解析】解:(1)由题意可知隐含条件3﹣m≥0,解得:m≤3,
∴m﹣5<0,
∴,
(2)由题意可知隐含条件x≥0,y﹣x≥0,解得:x≥0,y≥x,
∴y≥x≥0,
∴x+y≥0,
∴,
∴△ABC的周长为x+2y;
(3)由题意可知隐含条件x﹣4≥0,解得:x≥4,
当4≤x≤7时,x﹣7≤0,
则,符合题意,
当x>7时,x﹣7>0,
则,不符合题意,
综上所述,x的取值范围为4≤x≤7.
【点睛】本题考查了二次根式的性质和二次根式有意义的条件,熟练掌握二次根式的性质和二次根式有意义的条件是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题29 尺规作图与定义、命题、定理
一.选择题
1.(2024 恩施市模拟)下列语句中,不是命题的是( )
A.两直线平行,同旁内角相等 B.若2a=4,则a=2
C.过一点作已知直线的平行线 D.同角的余角相等
2.(2024 芙蓉区校级模拟)用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45° B.两个锐角都小于45°
C.两个锐角都不大于45° D.两个锐角都等于45°
3.(2024 北票市三模)下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x>y,则a2x>a2y.其中是真命题的是( )
A.②③ B.①② C.①②④ D.①②③④
4.(2024 珠海校级一模)下列命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.如果两个实数相等,那么它们的平方相等
C.等边三角形是锐角三角形 D.如果两个实数的积是正数,那么它们都是正数
5.(2024 吴兴区二模)在平面直角坐标系中有A(a,b)与B(b,a)两点(a、b≠0),关于过A、B两点的直线l与二次函数y=ax2+bx+1图象的交点个数判定,哪项为真命题( )
A.如果b>0,那么一定有两交点 B.只有b<0,才一定有两交点
C.如果a<0,那么一定有两交点 D.只有a>0,才一定有两交点
6.(2024 平湖市模拟)用尺规作图作一个角的角平分线,下列作法错误的是( )
A. B. C. D.
7.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
8.(2024 眉山)如图,在△ABC中,AB=AC=6,BC=4,分别以点A,点B为圆心,大于的长为半径作弧,两弧交于点E,F,过点E,F作直线交AC于点D,连结BD,则△BCD的周长为( )
A.7 B.8 C.10 D.12
9.(2024 金东区二模)如图,在△ABC中,∠C=90°,用直尺和圆规在边BC上确定一点P,使点P到边AC、AB的距离相等,则符合要求的作图痕迹是( )
A. B. C. D.
10.(2024 普陀区二模)在△ABC中,只用无刻度直尺和圆规比较∠B与∠C的大小.除了“叠合法”外,嘉琪又想出两种方法:
方法一:作△ABC的高AD和角平分线AE,若E点在线段BD上,则说明∠B<∠C.
方法二:作BC边中垂线MN,若MN与AB边相交(不包括A点),则说明∠B<∠C.
下列说法正确的是( )
A.方法一可行,方法二不可行 B.方法二可行,方法一不可行
C.两种方法都可行 D.两种方法都不可行
11.(2024 龙湾区二模)如图,在△ABC中,分别以点A,B为圆心,大于为半径画弧,两弧交于点E,F,作直线EF分别交BC,AB于点D,M,连结AD.若AC=4,CD=3,AD=5,则AB的长为( )
A. B. C.9 D.10
12.(2024 舟山三模)利用尺规作图在一个矩形内作菱形ABCD,则下列作法中错误的是( )
A. B. C. D.
13.(2024 拱墅区二模)如图,BD是△ABC的角平分线,分别以点B、D为圆心,以大于的长为半径在BD两侧作圆弧,交于点E,点F.作直线EF,分别交AB,BC于点G,H,连结DG,DH.设△ADG的面积为S1,四边形BGDH的面积为S2,若,则的值为( )
A. B. C. D.1
二.填空题
14.(2025 惠山区一模)命题“如果a<0,b<0,那么ab>0”的逆命题是 命题.
15.(2025 格尔木市校级一模)把命题“对顶角相等”改写成“如果……那么……”的形式: .
16.(2024 乐山模拟)命题“等角的余角相等”的逆命题是 ,这是一个 命题.(填“真”或“假”)
17.(2024 白山二模)用一个a的值说明“若a是实数,则2a一定比a大”是错误的,这个值可以是 .
18.(2024 临安区二模)关于一元二次方程ax2+bx+c=0(ac≠0),有以下命题:
①若a﹣b+c=0,则b2﹣4ac≥0;
②若该方程的两根为﹣3和1,则3a+c=0;
③若上述方程有两个相等的实数根,则ax2+bx+c=﹣1必有实数根;
④若r是该方程的一个根,则一定是方程cx2+bx+a=0的一个根.
其中真命题是 .(只需填写序号)
19.(2024 拱墅区一模)如图,AB∥CD.以点A为圆心,适当长为半径作弧,分别交AC,AB于点E,点F;再分别以点E,点F为圆心,大于为半径作弧,两圆弧交于点G;连接AG并延长交CD于点H,若∠AHD=115°,则∠C= °.
20.(2025 锦江区模拟)如图,在△ABC中,按以下步骤操作:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②以点C为圆心,以任意长为半径作弧,分别交AC,BC于点E,F;③分别以E,F为圆心,以大于的长为半径作弧,两弧交于点O;④作射线CO,交直线MN于点P,连接BP.若∠BAC=110°,∠ABP=7°,则∠PBC= .
三.解答题
21.(2024 广西)如图,在△ABC中,∠A=45°,AC>BC.
(1)尺规作图:作线段AB的垂直平分线l,分别交AB,AC于点D,E;(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接BE,若AB=8,求BE的长.
22.(2024 绍兴一模)图1,图2,图3均为4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的两个端点均为格点,只用无刻度的直尺,在给定的网格中画图,画出满足要求的一种情况即可.
(1)在图1中找一个格点P,连结BP,使∠ABP=45°.
(2)在图2中找两个格点P,Q,连结PQ,使直线PQ⊥AB.
(3)在图3中找两个格点P,Q,连结PQ交线段AB于点C,使AC=3BC.
23.(2024 普陀区二模)已知平行四边形ABCD,观察如图所示的尺规作图痕迹.
(1)求证:四边形ABEF是菱形;
(2)连结AE,若AE=6,BF=8,求菱形ABEF的周长.
24.(2024 定海区三模)阅读理解:
我们解决某些数学题的时候,经常会遇到题目中的条件比较含糊,它们常常巧妙地隐蔽在题设的背后,不易被发现和运用,导致我们解题受阻,因此,挖掘题设中的隐含条件,应该成为我们必备的一种能力.请阅读下面的解题过程,体会如何发现隐含条件,并依次解决所给的问题.
化简:.
解:由题意可知隐含条件1﹣5a≥0,解得:,
∴1﹣a>0,
∴.
启发应用:
(1)按照上面的解法,化简:;
类比迁移:
(2)已知△ABC的三边长分别为,,,请求出△ABC的周长.(用含有x、y的代数式表示,结果要求化简)
拓展延伸:
(3)若,请直接写出x的取值范围.
答案与解析
一.选择题
1.(2024 恩施市模拟)下列语句中,不是命题的是( )
A.两直线平行,同旁内角相等 B.若2a=4,则a=2
C.过一点作已知直线的平行线 D.同角的余角相等
【点拨】根据命题的定义作答.
【解析】解:根据命题的定义,可知A、B、D都是命题,
而C属于作图语言,不是命题.
故选:C.
【点睛】本题考查了命题的定义:一般的,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.一般说来,对于任何一个命题,都可以加上“是”或“不是”.注意,作图语言不是命题.
2.(2024 芙蓉区校级模拟)用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45° B.两个锐角都小于45°
C.两个锐角都不大于45° D.两个锐角都等于45°
【点拨】用反证法证明命题的真假,应先按符合题设的条件,假设题设成立,再判断得出的结论是否成立即可.
【解析】解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,
应先假设两个锐角都大于45°.
故选:A.
【点睛】本题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
3.(2024 北票市三模)下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x>y,则a2x>a2y.其中是真命题的是( )
A.②③ B.①② C.①②④ D.①②③④
【点拨】根据对顶角相等,平行线的判定,等式的性质,不等式的性质,逐一进行判断即可.
【解析】解:对顶角相等,故①为真命题;
同位角相等,两直线平行,故②为真命题;
若|a|=|b|,则a=b或a=﹣b,故③为假命题;
若x>y,当a≠0时,则a2x>a2y,故④为假命题.
故选:B.
【点睛】本题考查命题的真假,正确记忆相关知识点是解题关键.
4.(2024 珠海校级一模)下列命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.如果两个实数相等,那么它们的平方相等
C.等边三角形是锐角三角形 D.如果两个实数的积是正数,那么它们都是正数
【点拨】利用全等三角形的性质、实数的性质、等边三角形的性质等知识分别判断后即可确定正确的选项.
【解析】解:A、逆命题为对应角相等的三角形全等,不成立,不符合题意;
B、逆命题为如果两个数的平方相等,那么这两个数相等,不成立,不符合题意;
C、逆命题为锐角三角形是等边三角形,不成立,不符合题意;
D、逆命题为如果两个数都是正数,那么它们的积也是正数,成立,符合题意.
故选:D.
【点睛】考查了命题与定理,解题的关键是了解如何写出一个命题的逆命题,难度不大.
5.(2024 吴兴区二模)在平面直角坐标系中有A(a,b)与B(b,a)两点(a、b≠0),关于过A、B两点的直线l与二次函数y=ax2+bx+1图象的交点个数判定,哪项为真命题( )
A.如果b>0,那么一定有两交点 B.只有b<0,才一定有两交点
C.如果a<0,那么一定有两交点 D.只有a>0,才一定有两交点
【点拨】根据点A和点B的坐标,求出直线l的表达式,联立直线l与二次函数表达式,根据根的判别式求出一定有两个交点时必须满足条件b>0或a<0,然后分a+b=1和a+b≠1两种情况进行解答即可.
【解析】解:设直线l的表达式为:y=kx+m,
将点A,B的坐标代入表达式得:
,
解得:k=﹣1,m=a+b,
∴直线l的表达式为:y=﹣x+a+b,
联立二次函数表达式得:
﹣x+a+b=ax2+bx+1,
整理得:ax2+(b+1)x+1﹣a﹣b=0,
∴Δ=(b+1)2﹣4a(1﹣a﹣b)=4a2+4ab+b2﹣4a+2b+1=(2a+b﹣1)2+4b=(b+2a+1)2﹣8a,
要使Δ>0恒成立,∴b>0或a<0,
又二次函数y=ax2+bx+1的图象与y轴的交点坐标为(0,1),直线l:y=﹣x+a+b与y轴的交点坐标为(0,a+b),
∴当a+b≠1时,满足条件b>0或a<0,则直线l与二次函数y=ax2+bx+1的图象一定有两个交点,
当a+b=1时,直线l与二次函数y=ax2+bx+1的图象一定有一个定交点(0,1),
∵a+b=1,∴b=1﹣a,当a>0时,b<1,当a<0时,b>1,
若a<0,b>1,则直线l与二次函数y=ax2+bx+1的图象一定有两个交点,
若a>0,b<1,此时必须满足条件0<b<1,直线l与二次函数y=ax2+bx+1的图象才一定有两个交点,
若此时b<0,则直线l与二次函数y=ax2+bx+1的图象只有一个交点,即为(0,1),
∴只有a<0,才一定有两交点.
故选:C.
【点睛】本题考查了一次函数与二次函数的交点问题,熟练掌握根的判别式是解题的基础,确定a+b=1时的取值情况是解题的关键和难点.
6.(2024 平湖市模拟)用尺规作图作一个角的角平分线,下列作法错误的是( )
A. B. C. D.
【点拨】根据各个选项中的作图,可以判断哪个选项符合题意.
【解析】解:A.如图,
由作图可知,OA=OC,AB=BC,
又∵OB=OB,
∴△OAB≌△OCB(SSS),
∴∠AOB=∠COB,
∴OB平分∠AOC,
故选项A是在作角平分线,不符合题意;
B.如图,
由作图得,∠AOB=∠MBC,BO=BC,
∴BCAO,∠BOC=∠BCO,
∴∠AOC=∠BCO,
∴∠AOC=∠BOC,
∴OC 平分∠AOB,
故选项B是在作角平分线,不符合题意;
C.如图,
由作图知,点P是的中点,
∴,
∴∠NAP=∠MAP,
∴AP平分∠MAN,
故选项C是在作角平分线,不符合题意;
D.如图,
由作图知,AC与AB不一定相等,CP=BP,AP=AP,
∴△ACP与△ABP不全等,
∴∠CAP≠∠BAP,
∴AP不平分∠BAC,
∴AP 不是∠BAC 的平分线,
故选:D.
【点睛】本题考查作图—基本作图,解答本题的关键是明确角平分线的做法,利用数形结合的思想解答.
7.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
【点拨】由直角三角形两锐角互余可求出∠BAC=50°,由作图得∠BAD=25°,由三角形的外角的性质可得∠ADC=65°,故可得答案.
【解析】解:∵∠C=90°,∠B=40°,
∴∠BAC=90°﹣∠B=90°﹣40°=50°,
由作图知,AP平分∠BAC,
∴,
∵∠ADC=∠B+∠BAD,
∴∠ADC=40°+25°=65°,
故选:B.
【点睛】本题主要考查基本作图,直角三角形两锐角互余以及三角形外角的性质,掌握尺规作图的方法是解题的关键.
8.(2024 眉山)如图,在△ABC中,AB=AC=6,BC=4,分别以点A,点B为圆心,大于的长为半径作弧,两弧交于点E,F,过点E,F作直线交AC于点D,连结BD,则△BCD的周长为( )
A.7 B.8 C.10 D.12
【点拨】根据线段垂直平分线的性质得到AD=BD,根据三角形的周长公式即可得到结论.
【解析】解:由作图知,EF垂直平分AB,
∴AD=BD,
∴△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC,
∵AB=AC=6,BC=4,
∴△BCD的周长=6+4=10,
故选:C.
【点睛】本题考查了作图﹣基本作图,线段垂直平分线的性质,三角形周长的计算,熟练掌握线段垂直平分线的性质是解题的关键.
9.(2024 金东区二模)如图,在△ABC中,∠C=90°,用直尺和圆规在边BC上确定一点P,使点P到边AC、AB的距离相等,则符合要求的作图痕迹是( )
A. B. C. D.
【点拨】P到边AC、AB的距离相等,可知点P在∠A的平分线上,由此判断即可.
【解析】解:∵P到边AC、AB的距离相等,
∴点P在∠A的平分线上.
故选:C.
【点睛】本题考查作图﹣复杂作图,角平分线的性质等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.
10.(2024 普陀区二模)在△ABC中,只用无刻度直尺和圆规比较∠B与∠C的大小.除了“叠合法”外,嘉琪又想出两种方法:
方法一:作△ABC的高AD和角平分线AE,若E点在线段BD上,则说明∠B<∠C.
方法二:作BC边中垂线MN,若MN与AB边相交(不包括A点),则说明∠B<∠C.
下列说法正确的是( )
A.方法一可行,方法二不可行 B.方法二可行,方法一不可行
C.两种方法都可行 D.两种方法都不可行
【点拨】分别画出图形,结合角平分线的定义、垂线的定义、线段垂直平分线的性质、三角形内角和定理进行判断即可得出答案.
【解析】解:方法一:如图1所示,
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∴∠CAD+∠C=90°,∠DAB+∠B=90°,
∵∠CAD=∠CAE﹣∠DAE,∠DAB=∠BAE+∠DAE,
∴∠C=90°﹣∠CAE+∠DAE,∠B=90°﹣∠BAE﹣∠DAE,
∴∠B<∠C;
∵点D与点E可能重合,线段包含端点,
∴方法一不可行;
方法二:如图2所示,
∵MN垂直平分BC,
∴CN=BN,
∴∠B=∠NCB,
∵∠C>∠NCB,
∴∠C>∠B;
综上所述,方法一不可行,方法二可行;
故选:B.
【点睛】本题考查了角平分线的定义、垂线的定义、线段垂直平分线的性质、三角形内角和定理,熟练掌握角平分线与垂线的定义是解答本题的关键.
11.(2024 龙湾区二模)如图,在△ABC中,分别以点A,B为圆心,大于为半径画弧,两弧交于点E,F,作直线EF分别交BC,AB于点D,M,连结AD.若AC=4,CD=3,AD=5,则AB的长为( )
A. B. C.9 D.10
【点拨】根据勾股定理得到逆定理得到∠C=90°,根据相似三角形的判定和性质定理即可得到结论.
【解析】解:由作图知,直线EF垂直平分AB,
∴AD=BD,DM⊥AB,BM=AM,
∵AC2+CD2=42+32=52=AD2,
∴∠C=90°,
∵∠BMD=∠C=90°,∠B=∠B,
∴△BDM∽△BCA,
∴,
∴,
∴AB=4,
故选:B.
【点睛】本题考查了作图﹣基本作图,线段垂直平分线的性质,相似三角形的判定和性质,勾股定理的逆定理,熟练掌握线段垂直平分线的性质是解题的关键.
12.(2024 舟山三模)利用尺规作图在一个矩形内作菱形ABCD,则下列作法中错误的是( )
A. B. C. D.
【点拨】根据菱形的判定和作图痕迹解答即可.
【解析】解:A、由作图可知,AC⊥BD,即对角线平分且垂直的四边形是菱形,正确;
B、由作图可知AD=DC,即邻边相等的平行四边形是菱形,正确;
C、由作图可知AC⊥BD,对角线平分且垂直的四边形是菱形,正确;
D、由作图可知∠DAC=∠CAB,∠DCA=∠ACB,对角线AC平分对角,可以得出是菱形,错误;
故选:D.
【点睛】本题考查作图﹣复杂作图,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.
13.(2024 拱墅区二模)如图,BD是△ABC的角平分线,分别以点B、D为圆心,以大于的长为半径在BD两侧作圆弧,交于点E,点F.作直线EF,分别交AB,BC于点G,H,连结DG,DH.设△ADG的面积为S1,四边形BGDH的面积为S2,若,则的值为( )
A. B. C. D.1
【点拨】先判断是菱形,再根据相似三角形的性质及比例的性质.
【解析】解:由作图得:EF垂直平分BD,
∴BG=DG,BH=DH,
∵BD是△ABC的角平分线,
∴BG=BH,
∴BG=DG=BH=DH,
∴四边形BHDG是菱形,
∴DG∥BC,DH∥AB,
∴△ADG∽△ACB,△CDH∽△CAB,
设CH=2a,△ABC的面积为S,△CDH的面积为S3,
则DH=DG=BH=3a,
∴S1=S,S3=S,
∴S2=S﹣S1﹣S3=S,
∴S1:S2=S:S=,
故选:C.
【点睛】本题考查了基本作图,掌握菱形的判定定理和性质、角平分线的性质,及相似三角形的性质是解题的关键.
二.填空题
14.(2025 惠山区一模)命题“如果a<0,b<0,那么ab>0”的逆命题是 假 命题.
【点拨】把一个命题的条件和结论互换就得到它的逆命题,进而利用举反例判断命题正确性即可.
【解析】解:“若a<0,b<0,则ab>0”的逆命题是“若ab>0,则a<0,b<0”,是一个假命题.
故答案为:假.
【点睛】本题考查命题与定理,正确写出原命题的逆命题是解题关键.
15.(2025 格尔木市校级一模)把命题“对顶角相等”改写成“如果……那么……”的形式: 如果两个角是对顶角,那么这两个角相等 .
【点拨】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面即可.
【解析】解:把命题“对顶角相等”改写成“如果 那么 ”的形式为:如果两个角是对顶角,那么这两个角相等.
故答案为:如果两个角是对顶角,那么这两个角相等.
【点睛】本题考查了把一个命题写成“如果 那么 ”的形式,命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.
16.(2024 乐山模拟)命题“等角的余角相等”的逆命题是 如果两个角的余角相等,那么这两个角也相等 ,这是一个 真 命题.(填“真”或“假”)
【点拨】先把等角的余角相等写成“如果…那么…”的形式,然后交换题设和结论即可得到逆命题,再判断其真假.
【解析】解:“等角的余角相等”的逆命题为“如果两个角的余角相等,那么这两个角也相等”,这是一个真命题.
故答案为如果两个角的余角相等,那么这两个角也相等;真.
【点睛】本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题.
17.(2024 白山二模)用一个a的值说明“若a是实数,则2a一定比a大”是错误的,这个值可以是 ﹣1(答案不唯一) .
【点拨】根据实数的大小比较法则解答即可.
【解析】解:当a=﹣1时,2a=﹣2,
则2a<a,
可以说明“若a是实数,则2a一定比a大”是错误的,
故答案为:﹣1(答案不唯一).
【点睛】本题考查的是反证法以及假命题的证明,要证明一个命题是真命题,需要严格的证明过程,而要证明一个命题是假命题,只需要举一个反例即可.
18.(2024 临安区二模)关于一元二次方程ax2+bx+c=0(ac≠0),有以下命题:
①若a﹣b+c=0,则b2﹣4ac≥0;
②若该方程的两根为﹣3和1,则3a+c=0;
③若上述方程有两个相等的实数根,则ax2+bx+c=﹣1必有实数根;
④若r是该方程的一个根,则一定是方程cx2+bx+a=0的一个根.
其中真命题是 ①②④ .(只需填写序号)
【点拨】由a﹣b+c=0得b=a+c,即得b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,判断①是真命题;由该方程的两根为﹣3和1得﹣3×1=,c=﹣3a,即得3a+c=0,判断②是真命题;由ax2+bx+c=0有两个相等的实数根知b2﹣4ac=0,而ax2+bx+c+1=0的判别式:b2﹣4a×(c+1)=b2﹣4ac+4a=﹣4a,因a的符号不确定,故方程ax2+bx+c=﹣1根的情况不确定,判断③是假命题;由r是该方程的一个根得ar2+br+c=0,又r≠0,即可得a+b +c ()2=0,是cx2+bx+a=0的一个根,判断④是真命题.
【解析】解:若a﹣b+c=0,则b=a+c,
∴b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,故①是真命题;
若该方程的两根为﹣3和1,则﹣3×1=,
∴c=﹣3a,
∴3a+c=0,故②是真命题;
若ax2+bx+c=0有两个相等的实数根,则b2﹣4ac=0,
∴ax2+bx+c+1=0的判别式:b2﹣4a×(c+1)=b2﹣4ac﹣4a=﹣4a,
∵a的符号不确定,
∴方程ax2+bx+c=﹣1根的情况不确定,故③是假命题;
若r是该方程的一个根,则ar2+br+c=0,
∵ac≠0,
∴r≠0,
∴=0,
∴a+b +c ()2=0,
∴是cx2+bx+a=0的一个根,故④是真命题;
∴真命题有:①②④;
故答案为:①②④.
【点睛】本题考查命题与定理,解题的关键是掌握一元二次方程根的判别式和根与系数的关系.
19.(2024 拱墅区一模)如图,AB∥CD.以点A为圆心,适当长为半径作弧,分别交AC,AB于点E,点F;再分别以点E,点F为圆心,大于为半径作弧,两圆弧交于点G;连接AG并延长交CD于点H,若∠AHD=115°,则∠C= 50 °.
【点拨】由作图过程可知,AH为∠BAC的平分线,则∠BAH=∠CAH,根据平行线的性质可得∠BAH=∠CAH=180°﹣115°=65°,再由三角形的外角性质可得∠C=∠AHD﹣∠CAH=50°.
【解析】解:由作图过程可知,AH为∠BAC的平分线,
∴∠BAH=∠CAH,
∵AB∥CD,∠AHD=115°,
∴∠BAH=180°﹣115°=65°,
∴∠CAH=65°,
∴∠C=∠AHD﹣∠CAH=50°.
故答案为:50.
【点睛】本题考查作图—基本作图、平行线的性质,熟练掌握平行线的性质、角平分线的作图方法是解答本题的关键.
20.(2025 锦江区模拟)如图,在△ABC中,按以下步骤操作:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②以点C为圆心,以任意长为半径作弧,分别交AC,BC于点E,F;③分别以E,F为圆心,以大于的长为半径作弧,两弧交于点O;④作射线CO,交直线MN于点P,连接BP.若∠BAC=110°,∠ABP=7°,则∠PBC= 21° .
【点拨】由作图过程可知,直线MN为线段BC的垂直平分线,CP为∠ACB的平分线,可得PB=PC,∠ACP=∠BCP,即∠PBC=∠BCP=∠ACP,结合三角形内角和定理可得∠BAC+∠ABP+∠PBC+∠BCP+∠ACP=180°,进而可得答案.
【解析】解:由作图过程可知,直线MN为线段BC的垂直平分线,CP为∠ACB的平分线,
∴PB=PC,∠ACP=∠BCP,
∴∠PBC=∠BCP=∠ACP.
∵∠BAC+∠ABC+∠ACB=180°,
即∠BAC+∠ABP+∠PBC+∠BCP+∠ACP=180°,
∴110°+7°+3∠PBC=180°,
∴∠PBC=21°.
故答案为:21°.
【点睛】本题考查作图—基本作图、线段垂直平分线的性质、角平分线的定义、三角形内角和定理,熟练掌握线段垂直平分线的性质、角平分线的定义、三角形内角和定理是解答本题的关键.
三.解答题
21.(2024 广西)如图,在△ABC中,∠A=45°,AC>BC.
(1)尺规作图:作线段AB的垂直平分线l,分别交AB,AC于点D,E;(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接BE,若AB=8,求BE的长.
【点拨】(1)根据要求作出图形;
(2)证明△BDE是等腰直角三角形,可得结论.
【解析】解:(1)图形如图所示:
(2)∵DE垂直平分线段AB,
∴EB=EA,
∴∠EBA=∠A=45°,
∴∠BEA=90°,
∵BD=DA,
∴DE=DB=DA=AB=4,
∴BE=BD=4.
【点睛】本题考查作图﹣基本作图,线段的垂直平分线,等腰直角三角形的性质等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.
22.(2024 绍兴一模)图1,图2,图3均为4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的两个端点均为格点,只用无刻度的直尺,在给定的网格中画图,画出满足要求的一种情况即可.
(1)在图1中找一个格点P,连结BP,使∠ABP=45°.
(2)在图2中找两个格点P,Q,连结PQ,使直线PQ⊥AB.
(3)在图3中找两个格点P,Q,连结PQ交线段AB于点C,使AC=3BC.
【点拨】(1)以AB为斜边作等腰直角三角形,直角顶点即为所求的格点P.
(2)结合垂直的定义利用网格画图即可.
(3)取格点P,Q,使AP=3BQ,且AP∥BQ,则P,Q即为所求.
【解析】解:(1)如图1,P'和P''均满足题意.
(2)如图2,P,Q即为所求(答案不唯一).
(3)如图3,取格点P,Q,使AP=3BQ,且AP∥BQ,
此时△APC∽△BQC,
∴AC:BC=AP:BQ=3:1,
即AC=3BC,
则P,Q即为所求.
【点睛】本题考查作图—应用与设计作图、等腰直角三角形的判定与性质、相似三角形的判定与性质,解题的关键是理解题意,灵活运用所学知识解决问题.
23.(2024 普陀区二模)已知平行四边形ABCD,观察如图所示的尺规作图痕迹.
(1)求证:四边形ABEF是菱形;
(2)连结AE,若AE=6,BF=8,求菱形ABEF的周长.
【点拨】(1)先证明四边形是平行四边形,再证明是菱形;
(2)先根据勾股定理求出边长,再求出周长.
【解析】(1)证明:设BF交AE于点O,
在平行四边形ABCD中,有AD∥BC,
∴∠AFB=∠FBE,
由作图得:BE=BA,BF平分∠ABC,
∴∠ABF=∠EBF,
∴∠ABF=∠AFB,
∴AF=AB,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴ ABEF为菱形;
(2)证明:∵ ABEF为菱形;
∴AO==3,BO==4,∠AOB=90°,
AB=BE=EF=AF,
∴AB==5,
∴菱形ABEF的周长为:4×5=20.
【点睛】本题考查了基本作图,掌握菱形的判定定理和性质定理和勾股定理是解题的关键.
24.(2024 定海区三模)阅读理解:
我们解决某些数学题的时候,经常会遇到题目中的条件比较含糊,它们常常巧妙地隐蔽在题设的背后,不易被发现和运用,导致我们解题受阻,因此,挖掘题设中的隐含条件,应该成为我们必备的一种能力.请阅读下面的解题过程,体会如何发现隐含条件,并依次解决所给的问题.
化简:.
解:由题意可知隐含条件1﹣5a≥0,解得:,
∴1﹣a>0,
∴.
启发应用:
(1)按照上面的解法,化简:;
类比迁移:
(2)已知△ABC的三边长分别为,,,请求出△ABC的周长.(用含有x、y的代数式表示,结果要求化简)
拓展延伸:
(3)若,请直接写出x的取值范围.
【点拨】(1)先根据二次根式有意义的条件求出m的范围,再根据二次根式的性质化简即可;
(2)先根据二次根式有意义的条件求出x、y的范围,再根据二次根式的性质化简即可;
(3)先根据二次根式有意义的条件求出x的范围,再分类讨论,根据二次根式的性质化简即可.
【解析】解:(1)由题意可知隐含条件3﹣m≥0,解得:m≤3,
∴m﹣5<0,
∴,
(2)由题意可知隐含条件x≥0,y﹣x≥0,解得:x≥0,y≥x,
∴y≥x≥0,
∴x+y≥0,
∴,
∴△ABC的周长为x+2y;
(3)由题意可知隐含条件x﹣4≥0,解得:x≥4,
当4≤x≤7时,x﹣7≤0,
则,符合题意,
当x>7时,x﹣7>0,
则,不符合题意,
综上所述,x的取值范围为4≤x≤7.
【点睛】本题考查了二次根式的性质和二次根式有意义的条件,熟练掌握二次根式的性质和二次根式有意义的条件是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
