第6单元正比例和反比例易错精选题练习卷 2024-2025学年数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元正比例和反比例易错精选题练习卷 2024-2025学年数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 14:14:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例易错精选题练习卷-2024-2025学年数学六年级下册苏教版
一、选择题
1.下列式子中,x与y(x、y均不为0)成反比例的是( )。
A.=y B. C.x+y=12 D.12x=y
2.下面各组中的两种量,( )成反比例。
A.人的年龄和身高 B.六(1)班40名同学表演艺术操,每排的人数和排数
C.圆锥的底面积一定,体积和高 D.订阅《科学大众》的份数和总钱数
3.下面描述,错误的有( )句。
①0.15和0.150的大小和意义都相同。
②等腰梯形的两条腰相等,所以一个等腰梯形中不可能有3条相等的边。
③圆的面积与半径成正比例。
④一个非零自然数,不是奇数,就是偶数。
A.1 B.2 C.3 D.4
4.小明判断两种量是否成比例,成什么比例。他做对了( )题。
①实际距离一定,图上距离与比例尺。(成反比例)
②圆的面积与半径的平方。(成正比例)
③同一时间同一地点,杆高与其影长。(成正比例)
④每天加工零件的时间一定,每个零件加工的时间与加工的零件个数。(成正比例)
A.4 B.3 C.2 D.1
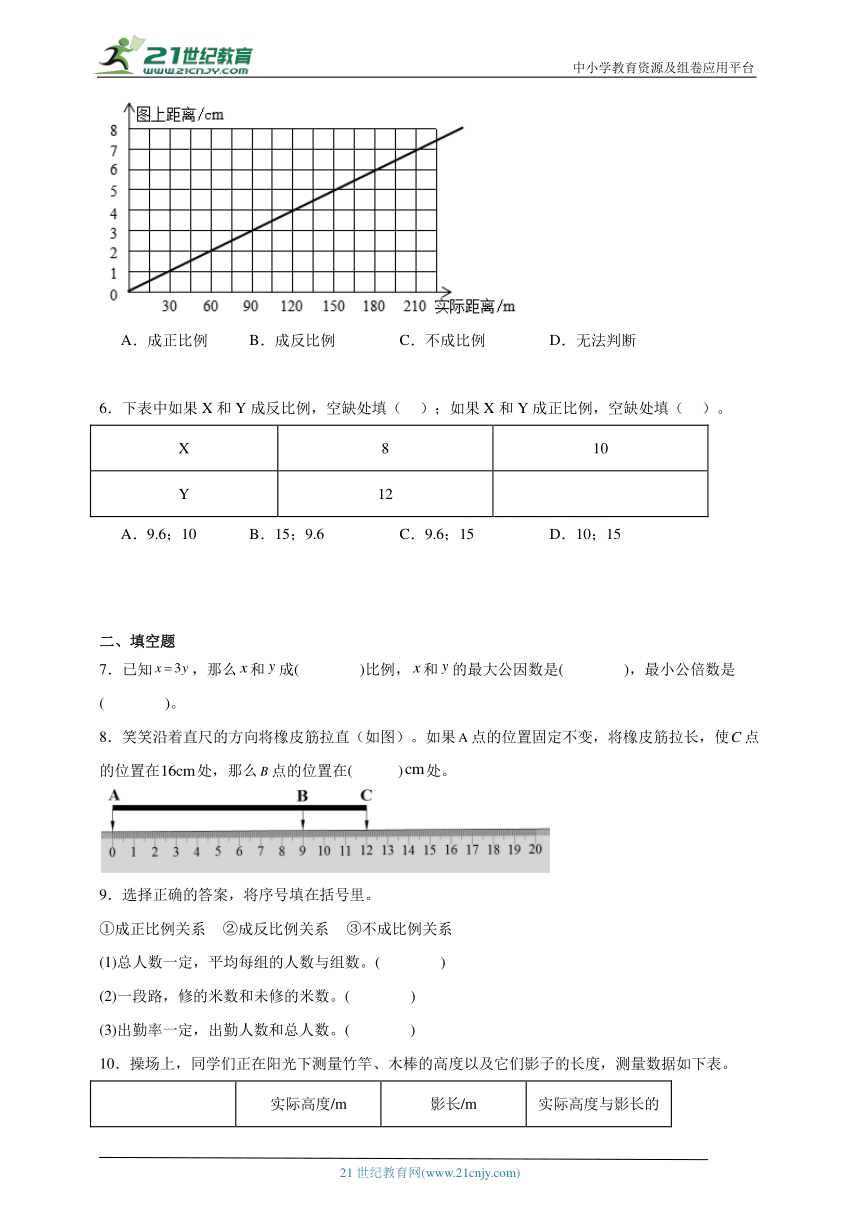
5.根据如图所示的图像可以知道,图上距离和实际距离( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
6.下表中如果X和Y成反比例,空缺处填( );如果X和Y成正比例,空缺处填( )。
X 8 10
Y 12
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
二、填空题
7.已知,那么和成( )比例,和的最大公因数是( ),最小公倍数是( )。
8.笑笑沿着直尺的方向将橡皮筋拉直(如图)。如果点的位置固定不变,将橡皮筋拉长,使点的位置在处,那么点的位置在( )处。
9.选择正确的答案,将序号填在括号里。
①成正比例关系 ②成反比例关系 ③不成比例关系
(1)总人数一定,平均每组的人数与组数。( )
(2)一段路,修的米数和未修的米数。( )
(3)出勤率一定,出勤人数和总人数。( )
10.操场上,同学们正在阳光下测量竹竿、木棒的高度以及它们影子的长度,测量数据如下表。
实际高度/m 影长/m 实际高度与影长的比值
竹竿1 2 0.5
竹竿2 1.6 0.4
木棒 1 0.25
计算并填写表格。仔细观察表格中竹竿、木棒的实际高度与影长的比值,你发现:_________________________。
11.当水与某种洗衣液的比是500∶9时洗衣效果最好,那么在80升水中需要加入( )毫升这种洗衣液效果才能最好。
12.下图是小郑和小南两人进行100米赛跑的情况。
(1)从图中可以看出,小郑跑的路程和时间成( )比例。
(2)小南每秒跑( )米;当小郑到达终点时,小南跑了( )米。
三、判断题
13.运一批货物,所需要的汽车数量和每辆运的吨数成正比例关系。( )
14.如果图像是一条曲线, 那么图像中表示各点的一对数就成反比例。( )
15.如果对xy=a(x≠0),当y一定时。a和x成正比例。( )
16.在1∶20000的地图上,图上距离和实际距离成正比例。( )
17.如果x和y成正比例,那么当x扩大时,y也随着扩大。( )
四、解答题
18.如下图,剪一根长14厘米的硬纸条,先找到纸条的中心点,再在中心点两侧每隔1厘米打一个孔,把纸条的中心固定在支架上。在支架右侧第4个孔处挂3个砝码(每个砝码重10克),想一想,在支架左侧第2个孔处挂多重的物体才能保持平衡?
19.学生们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用两种方法解答)
20.一辆汽车从工厂到工地,每小时行驶35千米,2小时可以到达。如果要4小时到达,每小时需要行驶多少千米?
21.佳航在操场上竖直固定了几根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长,情况如表:
竹竿长米 1 1.4 1.6 1.8 2.2 3
影长米 0.5 0.7 0.8 0.9 1.1 1.5
这时,佳航身边的强强测量出了旗杆的影长是6米,旗杆的实际高度是多少米?
22.一辆汽车准备从甲地开往乙地。根据下表提供的信息,把表格填写完整。
时间/时 8 10 16 20 32 40
速度(千米/时) 100 80
(1)行驶的时间和速度成什么比例关系?说明理由。
(2)试着在方格纸上画图表示表中的数据。
(3)如果这一辆汽车从甲地到乙地用了18小时,根据上面表格,估计这辆汽车的速度大约是多少?
《第6单元正比例和反比例易错精选题练习卷-2024-2025学年数学六年级下册苏教版》参考答案
题号 1 2 3 4 5 6
答案 A B C B A C
1.A
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫反比例关系。
【详解】A.=y
xy=12
12是一定值,所以x和y成反比例关系。
B.,12是一定值,所以x和y成正比例关系。
C.x+y=12,x和y不成比例。
D.12x=y
=12
12是一定值,所以x和y成正比例关系。
则上列式子中,x与y(x、y均不为0)成反比例的是=y。
故答案为:A
【点睛】此题考查了辨别正比例关系和反比例关系,要求学生掌握。
2.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.人的年龄和身高;人的年龄和身高的比值和乘积都不一定,所以人的年龄和身高不成比例;
B.六(1)班40名同学表演艺术操,每排的人数和排数;每排人数×排数=六(1)班40名同学表演艺术操(一定),每排的人数和排数成反比例;
C.圆锥的底面积一定,体积和高;圆锥的体积=底面积×高×;体积÷高=底面积×(一定),体积和高成正比例;
D.订阅《科学大众》的份数和总钱数;总钱数÷订阅《科学大众》的份数=《科学大众》的单价(一定),订阅《科学大众》的份数和总钱数成正比例。
下面各组中的两种量,六(1)班40名同学表演艺术操,每排的人数和排数成反比例。
故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
3.C
【分析】在小数的末尾添上零或者去掉零,小数的大小不变;等腰梯形的两条腰相等;圆的面积与半径的平方成正比例;一个非零自然数,不是奇数,就是偶数。
【详解】①0.15和0.150的大小相等,但是意义不相同,原题说法错误;
②等腰梯形的两条腰相等,特殊情况上底和两腰相等,此时这个等腰梯形中有3条相等的边,原题说法错误;
③圆的面积与半径的平方成正比例,原题说法错误;
④一个非零自然数,不是奇数,就是偶数,说法正确。
故答案为:C
【点睛】本题考查了小数的性质、等腰梯形的特征、及圆的面积与半径的关系及奇数和偶数的认识。
4.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】①图上距离÷比例尺=实际距离(一定),是对应的比值一定,图上距离与比例尺成正比例;
②圆的面积÷半径的平方=π(一定),是对应的比值一定,圆的面积和半径的平方成正比例。
③因为:物体影长÷竿高=每米物体的影长(一定),是对应的比值一定,所以同一地点、同一时间,竿高与它的影长成正比例;
④因为生产零件的总个数÷每个零件所用的时间=每天加工零件的时间一定(一定),
是对应的比值一定,符合正比例的意义,
所以当工作时间一定时,生产一个零件所用的时间和零件个数成正比例;
故答案为:B
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5.A
【分析】如果图像是一条经过原点的直线,则表示两个相关联的量成正比例关系。据此解题。
【详解】因为图像是一条经过原点的直线,所以图上距离和实际距离成正比例。
故答案为:A
【点睛】本题考查了正比例和反比例,明确正比例图像是一条经过原点的直线是解题的关键。
6.C
【分析】如果X和Y成反比例,则XY的乘积一定,求出8与12的积,再除以10即可;如果X和Y成正比例,则XY的比值一定,求出8与12的比值,再用10除以比值即可
【详解】8×12÷10
=96÷10
=9.6
8∶12=8÷12=
10÷
=10×
=15
即如果X和Y成反比例,空缺处填9.6;如果X和Y成正比例,空缺处填15。
故答案为:C
【点睛】本题主要考查正反比例的简单应用。
7. 正
【分析】两个量的比值一定,这两个量成正比例,两个量的乘积一定,这两个量成反比例。
两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
【详解】因为,所以,和的比值一定,成正比例。
因为、都是非零的自然数),所以和的最大公因数是,最小公倍数是。
8.12
【分析】根据题意可知,前后的长度与前后的长度成正比例关系,点原来在12厘米处,后来点的位置在16厘米处,点原来在9厘米处,依此设点的位置在厘米处,列比例即可求解。
【详解】设点的位置在厘米处,根据题意得:
,即此时点的位置在12厘米处。
9.(1)②
(2)③
(3)①
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行填空。
【详解】(1)平均每组人数×组数=总人数,总人数一定,平均每组的人数与组数②成反比例关系。
(2)修的米数+未修的米数=总长度,一段路,修的米数和未修的米数③不成比例关系。
(3)出勤人数÷总人数×100%=出勤率,出勤率一定,出勤人数和总人数①成正比例关系。
10.4;4;4
竹竿、木棒的实际高度与影长的比值一定,所以实际高度与影长成正比例关系。
【分析】(1)已知实际高度与影长的比,用比的前项除以比的后项即可得到比值。
(2)可以判断两个量成怎么样的比例关系,如果两个相关联的量,它们的比值(商)一定,则二者成正比例关系;如果两个相关联的量,它们的乘积一定,则二者成反比例关系;
【详解】2∶0.5=2÷0.5=4;1.6∶0.4=1.6÷0.4=4; 1∶0.25=1÷0.25=4。
实际高度/m 影长/m 实际高度与影长的比值
竹竿1 2 0.5 4
竹竿2 1.6 0.4 4
木棒 1 0.25 4
通过计算表格中的数据,发现2∶0.5=1.6∶0.4=1∶0.25=4(比值一定)
所以,竿、木棒的实际高度与影长的比值一定,所以实际高度与影长成正比例关系。
(答案不唯一,合理即可)
11.1440
【分析】要使洗衣液的效果最好,水与洗衣液的比值不变。设需要加入x毫升这种洗衣液,列出比例方程:500∶9=80∶x,再根据比例的基本性质解方程。注意单位要统一。
【详解】解:设需要加入x毫升这种洗衣液。
80升=80000毫升
500∶9=80000∶x
500×x=9×80000
500x=720000
500x÷500=720000÷500
x=1440
所以,在80升水中需要加入1440毫升这种洗衣液效果才能最好。
12.(1)正
(2) 3 75
【分析】(1)由图上可知小郑15秒跑了60米,25秒跑了100米,根据“速度=路程÷时间”计算得,速度是定值每秒4米,根据正比例的概念,判断解答。
(2)根据速度的计算公式求出小南的速度。小郑25秒达到终点,用小南的速度乘25秒即可得到小南跑了多少米。
【详解】(1)(米/秒)
(米/秒)
距离与时间的比值(速度)是一定的,所以小郑跑的路程和时间成正比例。
(2)(米/秒)
(米)
故小南每秒跑3米;当小郑到达终点时,小南跑了75米。
13.×
【分析】根据题意可知,货物的总吨数等于汽车数量乘每辆运的吨数,因此汽车数量和每辆运的吨数是成反比例关系。
【详解】根据分析可知,运一批货物,所需要的汽车数量和每辆运的吨数成反比例关系。
所以原题说法错误。
【点睛】这个题目考查正比例和反比例的认识,两个变量如果可以写成=k(k是不为零的常数),那么y和x成正比例;如果可以写成xy=k(k是不为零的常数),那么y和x成反比例。
14.×
【分析】根据正比例、反比例图像的特点解题,相关联的两个量,一个量随另一个量增大而减小,它们的积一定,这两种量叫做成反比例的量,它们成反比例关系,这两种相关联的量所绘成的图像是一条曲线,但是如果两个变量的乘积不一定,图像也可以是曲线,只是两个变量不成反比例。
【详解】根据分析可知,如果图像是一条曲线,那么图像中表示各点的一对数可能成反比例也可能不成比例,所以原题说法错误。
故答案为:×
【点睛】此题主要考查学生对反比例图像的形状和判断方法的理解与实际判断能力。
15.√
【分析】根据题意把等式变形,a和x是否是比值一定,如果比值一定则成正比例关系。
【详解】xy=a(x≠0),当y一定时,y= ,a和x的比值一定,所以a和x成正比例。原题说法正确。
故答案为:√
【点睛】判断两个量之间的关系,如果它们的比值一定,则成正比例关系;如果它们的乘积一定,则成反比例关系。
16.√
【分析】比例尺=,比值一定,成正比例关系,据此解答。
【详解】根据分析可得,在1∶20000的地图上,图上距离和实际距离成正比例,原题说法正确。
故答案为:√
【点睛】在同一幅地图上,比例尺是定值,图上距离和实际距离成正比例关系,积一定是反比例关系。
17.√
【解析】略
18.60克
【分析】用左右两侧物体的质量分别乘它们到中心点的距离,当结果相等时,才能保持平衡,据此解答。
【详解】4×3×10÷2
=12×10÷2
=120÷2
=60(克)
答:在支架左侧第2个孔处挂60克的物体才能保持平衡。
19.15行
【分析】第一种方法:原来每行人数×正好站成的行数=做操总人数,做操总人数÷现在每行站的人数=现在可以占的行数;
第二种方法:设可以站x行,总人数=每行站的人数×站成的行数;由于总人数不变,每行站的人数和行数成反比例。现在每行站的人数×现在可以站的行数=原来每行站的人数×正好站成的行数,列方程:24x=20×18,解方程,即可解答。
【详解】第一种:20×18÷24
=360÷24
=15(行)
第二种:解:设可以站x行。
24x=20×18
24x=360
24x÷24=360÷24
x=15
答:可以站15行。
【点睛】解答本题的关键明确总人数不变,利用总人数不变,进行解答。
20.17.5千米
【分析】本题甲地和乙地的总路程一定,因此速度×时间=总路程(一定),速度和时间成反比例,根据此列出方程,并解出方程即可。
【详解】解:设每小时需要行驶x千米
4x=35×2
4x=70
x=17.5
答:每小时需行驶17.5千米。
【点睛】此题考查的是反比例的应用。
21.12米
【分析】由于1÷0.5=2,1.4÷0.7=2,1.6÷0.8=2,由此即可知道同一时刻物高与影长成正比,可以设旗杆的实际高度是x米,当竹竿长是1米,影长0.5米时,即旗杆的高度∶旗杆的影长=1∶0.5,据此列出方程,求出未知数的值即可。
【详解】解:设旗杆的实际高度是米,
0.5x=6÷0.5
答:旗杆的实际高度是12米。
【点睛】找出等量关系,是解答此题的关键。
22.(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)见详解;
(3)44千米。
【分析】(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)根据路程、时间、速度三者之间的关系,求出对应的速度,填写表格。
(3)因为18小时介于16小时与20小时之间,那么速度就介于50与40之间,估算即可;
【详解】补充表格如下:
时间(时) 8 10 16 20 32 40
速度(千米/时) 100 80 50 40 25 20
(1)因为8×100=800(千米),10×80=800(千米),即路程一定,时间与速度成反比例;
(2)画图表示表中的数据:
(3)800÷18≈44(千米)
答:这辆汽车的速度大约是每小时44千米。
【点睛】运用表中给出的数据,结合路程、时间、速度三者之间的关系,解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例易错精选题练习卷-2024-2025学年数学六年级下册苏教版
一、选择题
1.下列式子中,x与y(x、y均不为0)成反比例的是( )。
A.=y B. C.x+y=12 D.12x=y
2.下面各组中的两种量,( )成反比例。
A.人的年龄和身高 B.六(1)班40名同学表演艺术操,每排的人数和排数
C.圆锥的底面积一定,体积和高 D.订阅《科学大众》的份数和总钱数
3.下面描述,错误的有( )句。
①0.15和0.150的大小和意义都相同。
②等腰梯形的两条腰相等,所以一个等腰梯形中不可能有3条相等的边。
③圆的面积与半径成正比例。
④一个非零自然数,不是奇数,就是偶数。
A.1 B.2 C.3 D.4
4.小明判断两种量是否成比例,成什么比例。他做对了( )题。
①实际距离一定,图上距离与比例尺。(成反比例)
②圆的面积与半径的平方。(成正比例)
③同一时间同一地点,杆高与其影长。(成正比例)
④每天加工零件的时间一定,每个零件加工的时间与加工的零件个数。(成正比例)
A.4 B.3 C.2 D.1
5.根据如图所示的图像可以知道,图上距离和实际距离( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
6.下表中如果X和Y成反比例,空缺处填( );如果X和Y成正比例,空缺处填( )。
X 8 10
Y 12
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
二、填空题
7.已知,那么和成( )比例,和的最大公因数是( ),最小公倍数是( )。
8.笑笑沿着直尺的方向将橡皮筋拉直(如图)。如果点的位置固定不变,将橡皮筋拉长,使点的位置在处,那么点的位置在( )处。
9.选择正确的答案,将序号填在括号里。
①成正比例关系 ②成反比例关系 ③不成比例关系
(1)总人数一定,平均每组的人数与组数。( )
(2)一段路,修的米数和未修的米数。( )
(3)出勤率一定,出勤人数和总人数。( )
10.操场上,同学们正在阳光下测量竹竿、木棒的高度以及它们影子的长度,测量数据如下表。
实际高度/m 影长/m 实际高度与影长的比值
竹竿1 2 0.5
竹竿2 1.6 0.4
木棒 1 0.25
计算并填写表格。仔细观察表格中竹竿、木棒的实际高度与影长的比值,你发现:_________________________。
11.当水与某种洗衣液的比是500∶9时洗衣效果最好,那么在80升水中需要加入( )毫升这种洗衣液效果才能最好。
12.下图是小郑和小南两人进行100米赛跑的情况。
(1)从图中可以看出,小郑跑的路程和时间成( )比例。
(2)小南每秒跑( )米;当小郑到达终点时,小南跑了( )米。
三、判断题
13.运一批货物,所需要的汽车数量和每辆运的吨数成正比例关系。( )
14.如果图像是一条曲线, 那么图像中表示各点的一对数就成反比例。( )
15.如果对xy=a(x≠0),当y一定时。a和x成正比例。( )
16.在1∶20000的地图上,图上距离和实际距离成正比例。( )
17.如果x和y成正比例,那么当x扩大时,y也随着扩大。( )
四、解答题
18.如下图,剪一根长14厘米的硬纸条,先找到纸条的中心点,再在中心点两侧每隔1厘米打一个孔,把纸条的中心固定在支架上。在支架右侧第4个孔处挂3个砝码(每个砝码重10克),想一想,在支架左侧第2个孔处挂多重的物体才能保持平衡?
19.学生们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用两种方法解答)
20.一辆汽车从工厂到工地,每小时行驶35千米,2小时可以到达。如果要4小时到达,每小时需要行驶多少千米?
21.佳航在操场上竖直固定了几根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长,情况如表:
竹竿长米 1 1.4 1.6 1.8 2.2 3
影长米 0.5 0.7 0.8 0.9 1.1 1.5
这时,佳航身边的强强测量出了旗杆的影长是6米,旗杆的实际高度是多少米?
22.一辆汽车准备从甲地开往乙地。根据下表提供的信息,把表格填写完整。
时间/时 8 10 16 20 32 40
速度(千米/时) 100 80
(1)行驶的时间和速度成什么比例关系?说明理由。
(2)试着在方格纸上画图表示表中的数据。
(3)如果这一辆汽车从甲地到乙地用了18小时,根据上面表格,估计这辆汽车的速度大约是多少?
《第6单元正比例和反比例易错精选题练习卷-2024-2025学年数学六年级下册苏教版》参考答案
题号 1 2 3 4 5 6
答案 A B C B A C
1.A
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫反比例关系。
【详解】A.=y
xy=12
12是一定值,所以x和y成反比例关系。
B.,12是一定值,所以x和y成正比例关系。
C.x+y=12,x和y不成比例。
D.12x=y
=12
12是一定值,所以x和y成正比例关系。
则上列式子中,x与y(x、y均不为0)成反比例的是=y。
故答案为:A
【点睛】此题考查了辨别正比例关系和反比例关系,要求学生掌握。
2.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.人的年龄和身高;人的年龄和身高的比值和乘积都不一定,所以人的年龄和身高不成比例;
B.六(1)班40名同学表演艺术操,每排的人数和排数;每排人数×排数=六(1)班40名同学表演艺术操(一定),每排的人数和排数成反比例;
C.圆锥的底面积一定,体积和高;圆锥的体积=底面积×高×;体积÷高=底面积×(一定),体积和高成正比例;
D.订阅《科学大众》的份数和总钱数;总钱数÷订阅《科学大众》的份数=《科学大众》的单价(一定),订阅《科学大众》的份数和总钱数成正比例。
下面各组中的两种量,六(1)班40名同学表演艺术操,每排的人数和排数成反比例。
故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
3.C
【分析】在小数的末尾添上零或者去掉零,小数的大小不变;等腰梯形的两条腰相等;圆的面积与半径的平方成正比例;一个非零自然数,不是奇数,就是偶数。
【详解】①0.15和0.150的大小相等,但是意义不相同,原题说法错误;
②等腰梯形的两条腰相等,特殊情况上底和两腰相等,此时这个等腰梯形中有3条相等的边,原题说法错误;
③圆的面积与半径的平方成正比例,原题说法错误;
④一个非零自然数,不是奇数,就是偶数,说法正确。
故答案为:C
【点睛】本题考查了小数的性质、等腰梯形的特征、及圆的面积与半径的关系及奇数和偶数的认识。
4.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】①图上距离÷比例尺=实际距离(一定),是对应的比值一定,图上距离与比例尺成正比例;
②圆的面积÷半径的平方=π(一定),是对应的比值一定,圆的面积和半径的平方成正比例。
③因为:物体影长÷竿高=每米物体的影长(一定),是对应的比值一定,所以同一地点、同一时间,竿高与它的影长成正比例;
④因为生产零件的总个数÷每个零件所用的时间=每天加工零件的时间一定(一定),
是对应的比值一定,符合正比例的意义,
所以当工作时间一定时,生产一个零件所用的时间和零件个数成正比例;
故答案为:B
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5.A
【分析】如果图像是一条经过原点的直线,则表示两个相关联的量成正比例关系。据此解题。
【详解】因为图像是一条经过原点的直线,所以图上距离和实际距离成正比例。
故答案为:A
【点睛】本题考查了正比例和反比例,明确正比例图像是一条经过原点的直线是解题的关键。
6.C
【分析】如果X和Y成反比例,则XY的乘积一定,求出8与12的积,再除以10即可;如果X和Y成正比例,则XY的比值一定,求出8与12的比值,再用10除以比值即可
【详解】8×12÷10
=96÷10
=9.6
8∶12=8÷12=
10÷
=10×
=15
即如果X和Y成反比例,空缺处填9.6;如果X和Y成正比例,空缺处填15。
故答案为:C
【点睛】本题主要考查正反比例的简单应用。
7. 正
【分析】两个量的比值一定,这两个量成正比例,两个量的乘积一定,这两个量成反比例。
两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
【详解】因为,所以,和的比值一定,成正比例。
因为、都是非零的自然数),所以和的最大公因数是,最小公倍数是。
8.12
【分析】根据题意可知,前后的长度与前后的长度成正比例关系,点原来在12厘米处,后来点的位置在16厘米处,点原来在9厘米处,依此设点的位置在厘米处,列比例即可求解。
【详解】设点的位置在厘米处,根据题意得:
,即此时点的位置在12厘米处。
9.(1)②
(2)③
(3)①
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行填空。
【详解】(1)平均每组人数×组数=总人数,总人数一定,平均每组的人数与组数②成反比例关系。
(2)修的米数+未修的米数=总长度,一段路,修的米数和未修的米数③不成比例关系。
(3)出勤人数÷总人数×100%=出勤率,出勤率一定,出勤人数和总人数①成正比例关系。
10.4;4;4
竹竿、木棒的实际高度与影长的比值一定,所以实际高度与影长成正比例关系。
【分析】(1)已知实际高度与影长的比,用比的前项除以比的后项即可得到比值。
(2)可以判断两个量成怎么样的比例关系,如果两个相关联的量,它们的比值(商)一定,则二者成正比例关系;如果两个相关联的量,它们的乘积一定,则二者成反比例关系;
【详解】2∶0.5=2÷0.5=4;1.6∶0.4=1.6÷0.4=4; 1∶0.25=1÷0.25=4。
实际高度/m 影长/m 实际高度与影长的比值
竹竿1 2 0.5 4
竹竿2 1.6 0.4 4
木棒 1 0.25 4
通过计算表格中的数据,发现2∶0.5=1.6∶0.4=1∶0.25=4(比值一定)
所以,竿、木棒的实际高度与影长的比值一定,所以实际高度与影长成正比例关系。
(答案不唯一,合理即可)
11.1440
【分析】要使洗衣液的效果最好,水与洗衣液的比值不变。设需要加入x毫升这种洗衣液,列出比例方程:500∶9=80∶x,再根据比例的基本性质解方程。注意单位要统一。
【详解】解:设需要加入x毫升这种洗衣液。
80升=80000毫升
500∶9=80000∶x
500×x=9×80000
500x=720000
500x÷500=720000÷500
x=1440
所以,在80升水中需要加入1440毫升这种洗衣液效果才能最好。
12.(1)正
(2) 3 75
【分析】(1)由图上可知小郑15秒跑了60米,25秒跑了100米,根据“速度=路程÷时间”计算得,速度是定值每秒4米,根据正比例的概念,判断解答。
(2)根据速度的计算公式求出小南的速度。小郑25秒达到终点,用小南的速度乘25秒即可得到小南跑了多少米。
【详解】(1)(米/秒)
(米/秒)
距离与时间的比值(速度)是一定的,所以小郑跑的路程和时间成正比例。
(2)(米/秒)
(米)
故小南每秒跑3米;当小郑到达终点时,小南跑了75米。
13.×
【分析】根据题意可知,货物的总吨数等于汽车数量乘每辆运的吨数,因此汽车数量和每辆运的吨数是成反比例关系。
【详解】根据分析可知,运一批货物,所需要的汽车数量和每辆运的吨数成反比例关系。
所以原题说法错误。
【点睛】这个题目考查正比例和反比例的认识,两个变量如果可以写成=k(k是不为零的常数),那么y和x成正比例;如果可以写成xy=k(k是不为零的常数),那么y和x成反比例。
14.×
【分析】根据正比例、反比例图像的特点解题,相关联的两个量,一个量随另一个量增大而减小,它们的积一定,这两种量叫做成反比例的量,它们成反比例关系,这两种相关联的量所绘成的图像是一条曲线,但是如果两个变量的乘积不一定,图像也可以是曲线,只是两个变量不成反比例。
【详解】根据分析可知,如果图像是一条曲线,那么图像中表示各点的一对数可能成反比例也可能不成比例,所以原题说法错误。
故答案为:×
【点睛】此题主要考查学生对反比例图像的形状和判断方法的理解与实际判断能力。
15.√
【分析】根据题意把等式变形,a和x是否是比值一定,如果比值一定则成正比例关系。
【详解】xy=a(x≠0),当y一定时,y= ,a和x的比值一定,所以a和x成正比例。原题说法正确。
故答案为:√
【点睛】判断两个量之间的关系,如果它们的比值一定,则成正比例关系;如果它们的乘积一定,则成反比例关系。
16.√
【分析】比例尺=,比值一定,成正比例关系,据此解答。
【详解】根据分析可得,在1∶20000的地图上,图上距离和实际距离成正比例,原题说法正确。
故答案为:√
【点睛】在同一幅地图上,比例尺是定值,图上距离和实际距离成正比例关系,积一定是反比例关系。
17.√
【解析】略
18.60克
【分析】用左右两侧物体的质量分别乘它们到中心点的距离,当结果相等时,才能保持平衡,据此解答。
【详解】4×3×10÷2
=12×10÷2
=120÷2
=60(克)
答:在支架左侧第2个孔处挂60克的物体才能保持平衡。
19.15行
【分析】第一种方法:原来每行人数×正好站成的行数=做操总人数,做操总人数÷现在每行站的人数=现在可以占的行数;
第二种方法:设可以站x行,总人数=每行站的人数×站成的行数;由于总人数不变,每行站的人数和行数成反比例。现在每行站的人数×现在可以站的行数=原来每行站的人数×正好站成的行数,列方程:24x=20×18,解方程,即可解答。
【详解】第一种:20×18÷24
=360÷24
=15(行)
第二种:解:设可以站x行。
24x=20×18
24x=360
24x÷24=360÷24
x=15
答:可以站15行。
【点睛】解答本题的关键明确总人数不变,利用总人数不变,进行解答。
20.17.5千米
【分析】本题甲地和乙地的总路程一定,因此速度×时间=总路程(一定),速度和时间成反比例,根据此列出方程,并解出方程即可。
【详解】解:设每小时需要行驶x千米
4x=35×2
4x=70
x=17.5
答:每小时需行驶17.5千米。
【点睛】此题考查的是反比例的应用。
21.12米
【分析】由于1÷0.5=2,1.4÷0.7=2,1.6÷0.8=2,由此即可知道同一时刻物高与影长成正比,可以设旗杆的实际高度是x米,当竹竿长是1米,影长0.5米时,即旗杆的高度∶旗杆的影长=1∶0.5,据此列出方程,求出未知数的值即可。
【详解】解:设旗杆的实际高度是米,
0.5x=6÷0.5
答:旗杆的实际高度是12米。
【点睛】找出等量关系,是解答此题的关键。
22.(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)见详解;
(3)44千米。
【分析】(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)根据路程、时间、速度三者之间的关系,求出对应的速度,填写表格。
(3)因为18小时介于16小时与20小时之间,那么速度就介于50与40之间,估算即可;
【详解】补充表格如下:
时间(时) 8 10 16 20 32 40
速度(千米/时) 100 80 50 40 25 20
(1)因为8×100=800(千米),10×80=800(千米),即路程一定,时间与速度成反比例;
(2)画图表示表中的数据:
(3)800÷18≈44(千米)
答:这辆汽车的速度大约是每小时44千米。
【点睛】运用表中给出的数据,结合路程、时间、速度三者之间的关系,解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
