一次函数检测卷(含解析)-2025年中考数学专项复习
文档属性
| 名称 | 一次函数检测卷(含解析)-2025年中考数学专项复习 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 20:17:40 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
一次函数检测卷-2025年中考数学专项复习
一、单选题
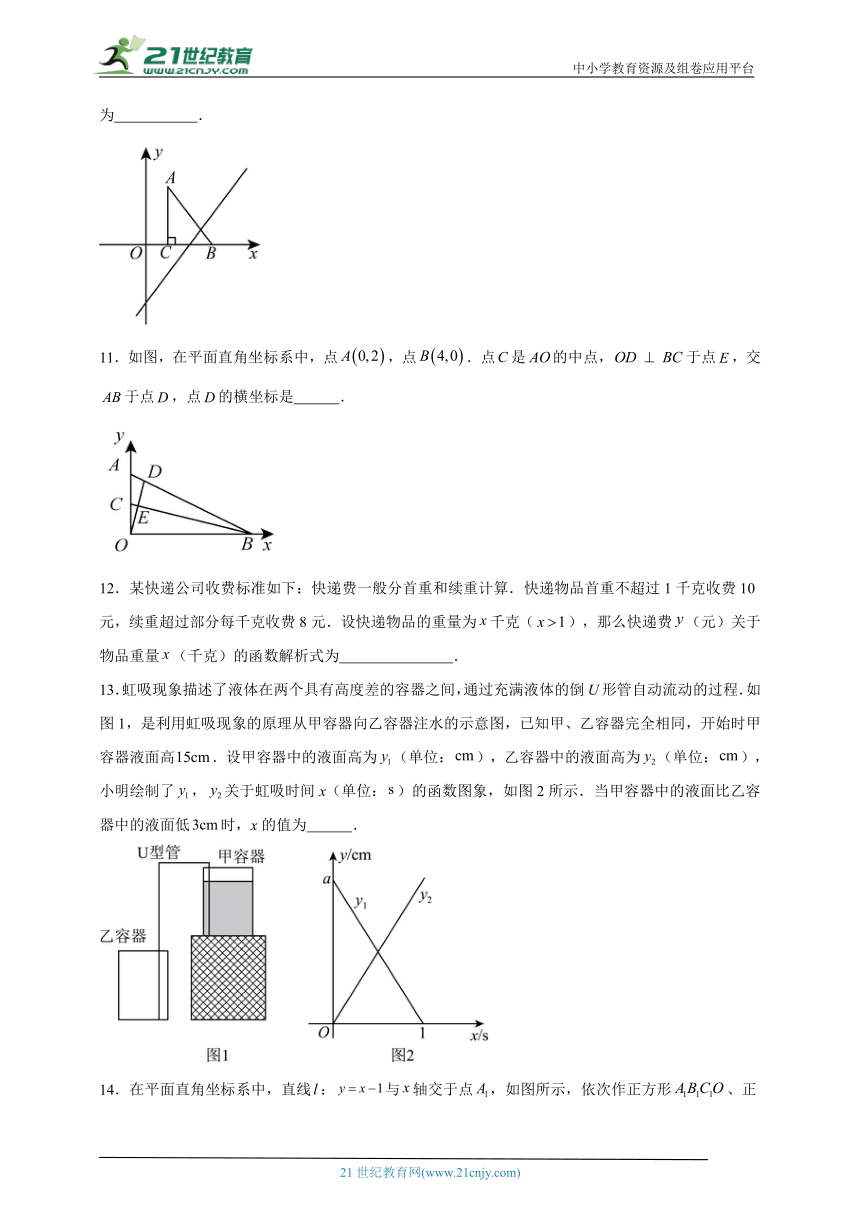
1.下列函数中,是一次函数的是( )
A. B. C. D.
2.一次函数的图象如图所示,当时,x的取值范围是( )
A. B. C. D.
3.直线的图象如图所示,则方程的解是( )
A. B. C. D.
4.一条笔直的公路上依次有A、B、C三地,甲车从A地驶往C地,乙车从A地驶往B地,两车同时出发并以各自的速度匀速行驶,乙车中途因故障停下来修理,修好后立即以原速的两倍继续前进到达B地;如图是甲、乙两车与A地的距离y(千米)(小时)之间的大致图象.下列说法错误的是( )
A.甲车的速度为 B.B、C两地之间的距离;
C.后乙追上甲 D.当两车相距40千米时,甲车行驶了或.
5.如图,三个函数的图象对应的表达式为:;;,则,,的大小关系是( )
A. B.
C. D.
6.如图,反比例函数的图象与正比例函数的图象交于点,将正比例函数的图象向上平移n个单位长度后,得到的直线与反比例函数的图象交于点,与y轴交于点,连接,则四边形的面积为( )
A.5 B. C. D.3
二、填空题
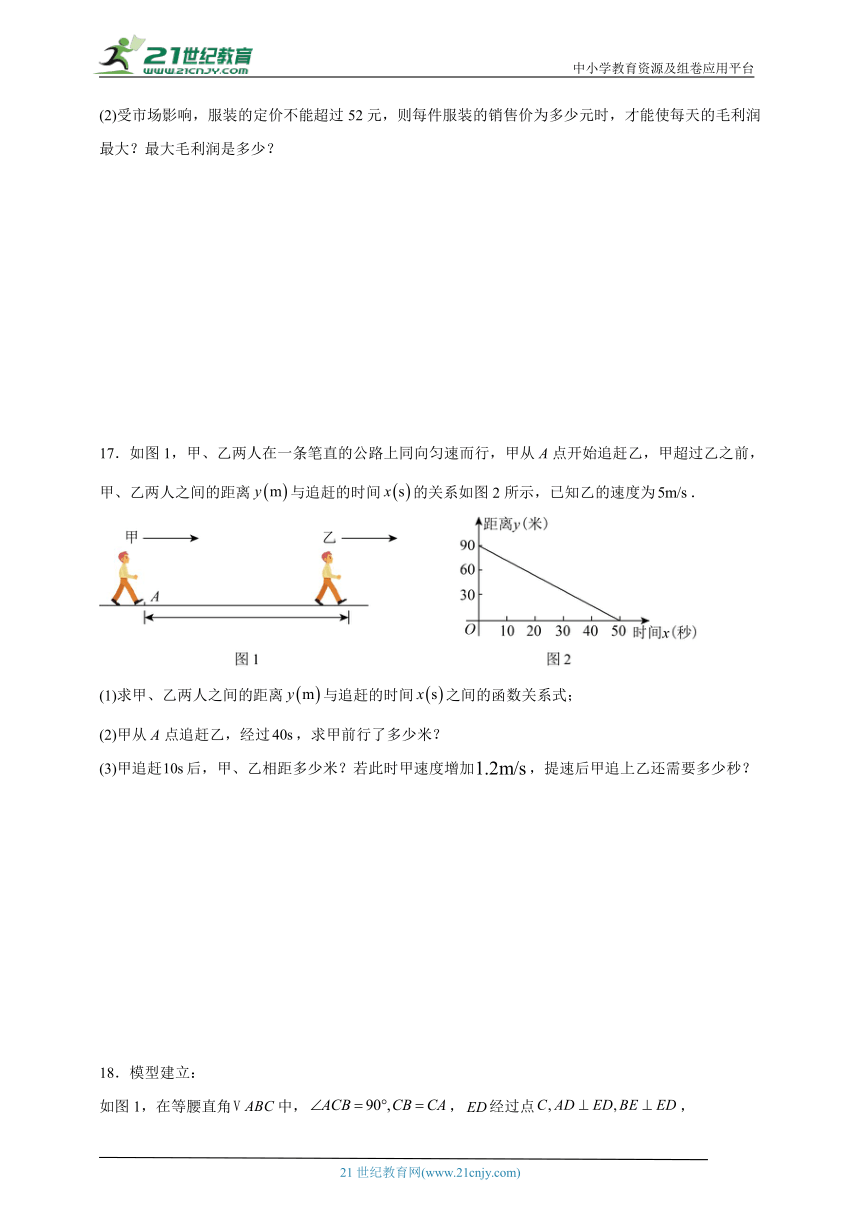
7.将直线向上平移,使之经过点,则平移后的函数图象是原函数图象向上平移 个单位长度得到的.
8.若函数是正比例函数,则 .
9.一次函数与的图象的交点的横坐标是2,则方程组的解为 .
10.如图,把放在直角坐标系中,其中,,点的坐标分别是和,将沿轴向右平移,当点落在直线上时,线段扫过的面积为 .
11.如图,在平面直角坐标系中,点,点.点是的中点,于点,交于点,点的横坐标是 .
12.某快递公司收费标准如下:快递费一般分首重和续重计算.快递物品首重不超过1千克收费10元,续重超过部分每千克收费8元.设快递物品的重量为千克(),那么快递费(元)关于物品重量(千克)的函数解析式为 .
13.虹吸现象描述了液体在两个具有高度差的容器之间,通过充满液体的倒U形管自动流动的过程.如图1,是利用虹吸现象的原理从甲容器向乙容器注水的示意图,已知甲、乙容器完全相同,开始时甲容器液面高.设甲容器中的液面高为(单位:),乙容器中的液面高为(单位:),小明绘制了,关于虹吸时间x(单位:)的函数图象,如图2所示.当甲容器中的液面比乙容器中的液面低时,x的值为 .
14.在平面直角坐标系中,直线:与轴交于点,如图所示,依次作正方形、正方形,正方形…,正方形,使得点、、、…、在直线上,点、、、…、在轴正半轴上,则点的横坐标是 .
三、解答题
15.已知A,B两地相距,甲、乙二人分别从A,B两地同时出发,相向而行.设甲、乙二人离A地的距离为,行驶时间为,则y与x的函数图象如图所示.
(1)分别求出、关于x的函数关系式;
(2)求乙到达A地时,甲距B地的距离;
(3)已知甲、乙两人早上八点同时出发,那么行驶过程中甲、乙二人何时相距?
16.某商场以每件42元的价格购进一批服装,由试销知,每天的销量t(件)与每件的销售价x(元)之间的函数关系如图所示:
(1)求每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式;(毛利润销售总额进货成本)
(2)受市场影响,服装的定价不能超过52元,则每件服装的销售价为多少元时,才能使每天的毛利润最大?最大毛利润是多少?
17.如图1,甲、乙两人在一条笔直的公路上同向匀速而行,甲从A点开始追赶乙,甲超过乙之前,甲、乙两人之间的距离与追赶的时间的关系如图2所示,已知乙的速度为.
(1)求甲、乙两人之间的距离与追赶的时间之间的函数关系式;
(2)甲从A点追赶乙,经过,求甲前行了多少米?
(3)甲追赶后,甲、乙相距多少米?若此时甲速度增加,提速后甲追上乙还需要多少秒?
18.模型建立:
如图1,在等腰直角中,,经过点,
说明的理由.
模型应用:
如图2,已知直线与轴、轴分别交于两点,以为顶点在第二象限作等腰直角,求出直线的函数关系式.
拓展应用:
如图3,在长方形中,点,点是线段上的一动点,,已知点在第一象限,是直线上的一点,若是等腰直角三角形,且,求点的坐标,
19.如图所示,根据图中信息.
(1)点P的坐标为 .
(2)当时,x的取值范围是多少?
(3)求.
20.如图,平面直角坐标系中,,,A、C分别在x轴的正、负半轴上.过点C的直线绕点C旋转,交y轴于点D,交线段于点E.
(1)直接写出A、C的坐标;
(2)写出直线的解析式;
(3)若与的面积相等,求点E的坐标.
21.【概念学习】
对于平面直角坐标系中的图形K和图形W,给出如下定义:R,S分别为图形K和图形W上任意一点,将R,S两点间距离的最小值称为图形K和图形W之间的“关联距离”,记作.例如,如图1,点与y轴之间的“关联距离”.
【理解概念】
(1)如图1,点在边长为5的正方形内,则d(T,正方形)=________;
【深入探索】
(2)如图2,一次函数图象与y轴交于点E,与x轴交于点F,若点和一次函数的图象之间的“关联距离”,求m的值;
(3)如图3,在等边中,点A的坐标是,点B,C在y轴上,点H是x轴上一点,若,请直接写出点H的坐标.
【拓展延伸】
(4)在中,,,,当时,对于每一个n,若和一次函数(k是常数,)的图象之间的“关联距离”,请直接写出k的取值范围.
《一次函数检测卷-2025年中考数学专项复习》参考答案
题号 1 2 3 4 5 6
答案 C A B D D B
1.C
【分析】本题考查了一次函数的定义,熟练掌握一次函数的定义是解题的关键;根据一次函数的定义条件进行逐一分析即可.
【详解】解:A.函数其形式为(为常数,) ,不符合一次函数(,为常数,)的形式,故该选项不符合题意;
B.函数是其自变量的最高次数是 ,不符合一次函数自变量最高次数为的要求,故该选项不符合题意;
C.函数可变形为 ,符合一次函数(,,)的形式,故该选项符合题意;
D.函数是常数函数,无论取何值,的值恒为 ,不符合一次函数的形式,故该选项不符合题意;
故选:C.
2.A
【分析】本题考查一次函数与一元一次不等式,根据一次函数的图象,进行求解即可.
【详解】解:由图象可知,随的增大而减小,当时,,
∴当时,的取值范围是;
故选A.
3.B
【分析】本题考查了一次函数图像与一元一次方程的关系,熟练运用数形结合思想是解题的关键.
【详解】解:∵在的图象上,
∴方程的解是
故选:B.
4.D
【分析】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,路程、速度、时间三者之间的关系.A、B、根据题意,结合图象列式计算即可;C、设乙t小时追上甲,根据甲行驶的路程=乙行驶的路程,列出方程解答便可;D、利用待定系数法分别求出时,,时函数关系式,再列方程解答即可.
【详解】解:甲车的速度为,故选项A正确,不符合题意;
乙前面的速度为:,
乙后来的速度为:,
,
则B、C两地之间的距离为,故选项B正确,不符合题意;
设乙t小时追上甲,
根据题意得,
解得,
则出发后乙追上甲,故选项C正确,不符合题意;
当时,两车距离小于40,
①当时,
设甲距离A地的距离与出发时间之间的关系式为,
代入可得,
,
,解得;
②当时,
由(1)可得,A、B两地之间的距离为:,
设乙与A地距离与出发时间x之间的函数关系式为,
代入和,
得,解得:,
,
解方程得(不合题意,舍去),
解方程得;
③当时,
解方程得,
当两车相距40千米时,甲车行驶了或或,故选项D错误,不符合题意.
故选:D.
5.D
【分析】本题考查了正比例函数图象的性质,掌握函数图象的性质是解题的关键.
根据正比例函数图象的性质即可求解.
【详解】解:∵图象在第二、四象限,
∴,
∵,图象在第一、三象限,,,
∵直线在第一、三象限越陡,则越大,
∴,
∴,
故选:.
6.B
【分析】本题考查的是一次函数的平移,反比例函数的图象与性质,反比例函数比例系数k的几何意义;先求解反比例函数为:,正比例函数为,直线为,,再进一步求解即可.
【详解】解:∵反比例函数的图象与正比例函数的图象交于点,
∴,,
解得:,
∴反比例函数为:,正比例函数为,
∵将正比例函数的图象向上平移n个单位长度后,得到的直线与反比例函数的图象交于点,
∴,即,一次函数为,
∴,
解得:,
∴直线为,
当时,,
∴,
如图,过作轴于,作轴于,过作轴于,
∴五边形的面积为,
∴四边形的面积为;
故选:B.
7.3
【分析】本题主要考查了一次函数图象的平移问题,求一次函数解析式,设将直线向上平移m个单位后得到的直线经过点,则平移后的直线解析式为,据此利用待定系数法求解即可.
【详解】解:设将直线向上平移m个单位后得到的直线经过点,
∴平移后的直线解析式为,
∴,
∴,
故答案为:3.
8.2
【分析】本题考查的是正比例函数的定义,熟知正比例函数的定义是解答此题的关键.
一般地,形如(k是常数,)的函数叫做正比例函数,其中k叫做比例系数,据此解答即可.
【详解】解:∵函数是正比例函数,
∴,且,
∴.
故答案为:2.
9.
【分析】本题主要考查了一次函数与二元一次方程组的知识,依据题意,两个函数图象的交点横坐标为2,则可得纵坐标为2,又方程组的解就是两个函数图象交点的横坐标与纵坐标的值,进而可以得解.
【详解】解:由题意,∵一次函数与的图象的交点的横坐标是2,
∴交点的纵坐标为,
则方程组的解为,
故答案为:.
10.12
【分析】此题考查平移的性质及一次函数的综合应用,二次根式的乘法运算,解决本题的关键是明确线段扫过的面积的计算.根据题意,线段扫过的面积的四边形面积,其高是的长,底是点平移的路程.求当点落在直线上时的横坐标即可.
【详解】解:如图所示.
点的坐标分别是和,
∴.
,,
∴由勾股定理可得:.
∴.
点在直线上,
,解得.
即.
∴.
.
即线段扫过的面积为12.
故答案为:.
11.
【分析】本题考查了解直角三角形,一次函数解析式,过点作于点F,先证明,根据,得到,利用正切的定义结合点是的中点,求出,设,求出直线的解析式,代入直线的解析式,即可求解.
【详解】解:过点作于点F,
∵,,
∴,,,
∴,
∵,
∴,
∴,
∴,
∴,
∵点,点.点是的中点,
∴,
∴,
∴,
∴,
设,直线的解析式为,则
,
解得:,
∴直线的解析式为,
将代入,
则,
解得:,
∴点的横坐标是,
故答案为:.
12.
【分析】本题考查一次函数的应用.根据题意,可以写出y与x之间的函数关系式.
【详解】解:当时,,
∴y与x之间的函数关系式为:.
故答案为:.
13./
【分析】本题考查了一次函数的应用.利用待定系数法求得,再利用甲容器向乙容器注水,始终有,求得,根据题意列方程求解即可.
【详解】解:当时,,
∵开始时甲容器液面高,
∴,
又∵时,,
∴设,
将代入得,解得,
∴,
∵甲容器向乙容器注水,始终有,
∴,
∴甲容器中的液面比乙容器中的液面低时,即,
∴,
解得,
故答案为:.
14.
【分析】本题考查了一次函数的性质,正方形的性质,点坐标规律探索,熟练掌握以上知识点是解答本题的关键.
首先找到直线与轴的交点,然后根据正方形的性质确定后续点的坐标,最后总结出的坐标规律,即可解答.
【详解】解:令,解得,
,
四边形是正方形,
;
当时,,
,
当时,,
,
,
观察规律发现,,,,,
的横坐标是,
故答案为:.
15.(1),
(2)
(3)11时或13时
【分析】本题考查了一次函数的应用,正确读取信息,熟练掌握待定系数法是解题的关键.
(1)利用待定系数法解答即可.
(2)根据两人相遇前,相遇后两种情形,解方程即可.
【详解】(1)解:设,
根据题意,得,
解得,
故;
当时,,
故图象交点的坐标为,
设,根据题意,
得,
解得,
∴,
(2)解:∴,
解得,
∴,
则,
故乙到达A地时,甲距B地的距离为.
(3)解:设经过,甲、乙相距90千米,
①甲乙相遇前,
根据题意,得则,
解得(小时),此时为11时.
②甲乙相遇后,
根据题意,得则,
解得(小时),此时为13时.
综上:行驶过程中甲、乙二人在11时或13时相距.
16.(1)
(2)每件服装的销售价为52元时,才能使每天的毛利润最大,最大毛利润是240元
【分析】本题主要考查二次函数的应用,求一次函数解析式,理解题意根据相等关系列出函数关系式,并熟练掌握二次函数的性质是解题的关键.
(1)首先利用待定系数法求出,然后表示出y即可;
(2)根据二次函数的性质求解即可.
【详解】(1)解:设每天的销量t(件)与每件的销售价x(元)之间的函数关系式为
根据题意得,
解得
∴
∴;
(2)∵
∴对称轴为直线
∵
∴抛物线开口向下
∴当时,y随x的增大而增大
∵受市场影响,服装的定价不能超过52元
∴当时,y取得最大值,最大值为
∴每件服装的销售价为52元时,才能使每天的毛利润最大,最大毛利润是240元.
17.(1);
(2);
(3).
【分析】本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式.
(1)先设出函数解析式,然后根据图象中数据,即可求得该函数的解析式;
(2)根据图象中的数据,可以求得甲的速度,然后即可计算出甲从A点追赶乙,经过走的路程;
(3)将代入(1)中的函数解析式求出相应的y的值,然后根据(2)中甲的速度,可以求出加速后的速度,最后即可计算出提速后甲追上乙还需要多少秒.
【详解】(1)解:设甲、乙两人之间的距离与追赶的时间之间的函数关系式为,
∵点,在该函数图象上,
∴,
解得,
即甲、乙两人之间的距离与追赶的时间之间的函数关系式为;
(2)解:甲的速度为:(),
则甲从A点追赶乙,经过,甲走的路程为:(米),
答:甲从A点追赶乙,经过,甲前行了272米;
(3)解:将代入,得,
设甲提速后,追上乙需要m秒,
(秒),
答:甲追赶10s后,甲、乙相距72米,若此时甲速度增加,提速后甲追上乙还需要24秒.
18.(1)见详解(2)(3)或.
【分析】本题考查了一次函数与几何图形综合,三角形全等等知识,解决问题的关键是构造全等模型.
(1)由,得,进而得证;
(2)先求出的坐标,过点C作轴于点H,先证明,再求出点C的坐标,进而利用待定系数法求的解析式即可.
(3)作于,于,构造模型,设点,,,得进而得出点.
【详解】解:(1)∵,,
,
,
,
,
,
又,
;
(2)令,则,令,则,
则点A、B的坐标分别为∶、,
过点C作轴于点H,
∵,,
∴
又∵,
∴,
∴,,
则点,
设的解析式为:,
把,代入,
则
解得∶
故直线的表达式为∶
(3)如图3,
作于,于,
设点,
,
,
由上知,,
,
当时,
当时,,,
,
点和重合,
.
综上所述,或.
19.(1)
(2)
(3)4
【分析】本题主要考查了一次函数的性质、一次函数与二元一次方程组、坐标与图形等知识点,掌握一次函数与二元一次方程组的关系是解答本题的关键.
(1)把代入可计算出m的值,把代入可求出n的值,联立两解析式所组成的方程组即可得到P点坐标;
(2)观察函数图像得到,当x大于P点的横坐标时,,据此即可解答.
(3)直接根据坐标与图形和三角形面积公式列式计算即可.
【详解】(1)解:把代入中得,解得,
∴,
把代入得,解得,
∴,
联立,解得,
∴;
(2)解:由函数图象可得,当时,;
(3)解:令,则,则,即,
∴,
∴.
20.(1)、
(2)
(3)
【分析】本题考查了待定系数法求一次函数的解析式,坐标与图形的性质,三角形的面积等知识点,数形结合是解此题的关键.
(1)根据,求解即可;
(2)用待定系数法即可求出直线的解析式;
(3)推出和的面积相等,根据面积公式求出E的纵坐标.
【详解】(1)解:∵,,
∴,
∴,;
(2)解:设直线的解析式为.
∴
解得
∴直线的解析式为;
(3)解:∵,
∴,
即,
∵点E在线段上,
∴点E在第一象限,且,
∴
∴
把代入直线的解析式得:
∴
∴.
21.(1)2;(2)m的值为或;(3),,;(4)且
【分析】(1)根据“关联距离”的定义求解即可;
(2)根据题意得点在直线l即上,过点G作,连接,结合图形,利用勾股定理及等面积法求解即可得出结果;
(3)分三种情况画出图形:当H在右侧时,当H在线段上时,当H在左侧时,作出相应图形求解即可;
(4)根据题意得出直线过定点,作出,确定当时,平移到,然后结合图形即可求解.
【详解】解:(1)与边长为5的正方形的边上的点的最小距离为2,
根据“关联距离”的定义得:d(T,正方形),
故答案为:2;
(2)根据题意得点在直线l即上,
过点G作,连接,如图所示:
∵,
当时,,当时,,
∴,
∴,
∵,
∴,
∴
解得:,
∴;
当时,
解得:
∴,结合图形得:
点与点G关于点C对称,
∴,
∴;
综上可得或,
即m的值为或;
(2)当H在右侧时,如图:
,
,
的坐标是,
的坐标是;
当H在线段上时,过H作于D,如图:
,
,
是等边三角形,,
,
,
的坐标是,
,
的坐标是;
当H在左侧时,如图:
,
,
;
综上所述,H的坐标为或或;
(3)
当时,,
直线过定点,
当时,,,,
当时,,,,
做出相应图形为:
当时,平移到,
把代入得:,
解得,
把代入得:,
解得,
∴结合图形得,
∴且.
【点睛】本题考查一次函数的综合应用,涉及新定义,等边三角形,平行四边形等知识,解题的关键是分类讨论思想和数形结合思想的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
一次函数检测卷-2025年中考数学专项复习
一、单选题
1.下列函数中,是一次函数的是( )
A. B. C. D.
2.一次函数的图象如图所示,当时,x的取值范围是( )
A. B. C. D.
3.直线的图象如图所示,则方程的解是( )
A. B. C. D.
4.一条笔直的公路上依次有A、B、C三地,甲车从A地驶往C地,乙车从A地驶往B地,两车同时出发并以各自的速度匀速行驶,乙车中途因故障停下来修理,修好后立即以原速的两倍继续前进到达B地;如图是甲、乙两车与A地的距离y(千米)(小时)之间的大致图象.下列说法错误的是( )
A.甲车的速度为 B.B、C两地之间的距离;
C.后乙追上甲 D.当两车相距40千米时,甲车行驶了或.
5.如图,三个函数的图象对应的表达式为:;;,则,,的大小关系是( )
A. B.
C. D.
6.如图,反比例函数的图象与正比例函数的图象交于点,将正比例函数的图象向上平移n个单位长度后,得到的直线与反比例函数的图象交于点,与y轴交于点,连接,则四边形的面积为( )
A.5 B. C. D.3
二、填空题
7.将直线向上平移,使之经过点,则平移后的函数图象是原函数图象向上平移 个单位长度得到的.
8.若函数是正比例函数,则 .
9.一次函数与的图象的交点的横坐标是2,则方程组的解为 .
10.如图,把放在直角坐标系中,其中,,点的坐标分别是和,将沿轴向右平移,当点落在直线上时,线段扫过的面积为 .
11.如图,在平面直角坐标系中,点,点.点是的中点,于点,交于点,点的横坐标是 .
12.某快递公司收费标准如下:快递费一般分首重和续重计算.快递物品首重不超过1千克收费10元,续重超过部分每千克收费8元.设快递物品的重量为千克(),那么快递费(元)关于物品重量(千克)的函数解析式为 .
13.虹吸现象描述了液体在两个具有高度差的容器之间,通过充满液体的倒U形管自动流动的过程.如图1,是利用虹吸现象的原理从甲容器向乙容器注水的示意图,已知甲、乙容器完全相同,开始时甲容器液面高.设甲容器中的液面高为(单位:),乙容器中的液面高为(单位:),小明绘制了,关于虹吸时间x(单位:)的函数图象,如图2所示.当甲容器中的液面比乙容器中的液面低时,x的值为 .
14.在平面直角坐标系中,直线:与轴交于点,如图所示,依次作正方形、正方形,正方形…,正方形,使得点、、、…、在直线上,点、、、…、在轴正半轴上,则点的横坐标是 .
三、解答题
15.已知A,B两地相距,甲、乙二人分别从A,B两地同时出发,相向而行.设甲、乙二人离A地的距离为,行驶时间为,则y与x的函数图象如图所示.
(1)分别求出、关于x的函数关系式;
(2)求乙到达A地时,甲距B地的距离;
(3)已知甲、乙两人早上八点同时出发,那么行驶过程中甲、乙二人何时相距?
16.某商场以每件42元的价格购进一批服装,由试销知,每天的销量t(件)与每件的销售价x(元)之间的函数关系如图所示:
(1)求每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式;(毛利润销售总额进货成本)
(2)受市场影响,服装的定价不能超过52元,则每件服装的销售价为多少元时,才能使每天的毛利润最大?最大毛利润是多少?
17.如图1,甲、乙两人在一条笔直的公路上同向匀速而行,甲从A点开始追赶乙,甲超过乙之前,甲、乙两人之间的距离与追赶的时间的关系如图2所示,已知乙的速度为.
(1)求甲、乙两人之间的距离与追赶的时间之间的函数关系式;
(2)甲从A点追赶乙,经过,求甲前行了多少米?
(3)甲追赶后,甲、乙相距多少米?若此时甲速度增加,提速后甲追上乙还需要多少秒?
18.模型建立:
如图1,在等腰直角中,,经过点,
说明的理由.
模型应用:
如图2,已知直线与轴、轴分别交于两点,以为顶点在第二象限作等腰直角,求出直线的函数关系式.
拓展应用:
如图3,在长方形中,点,点是线段上的一动点,,已知点在第一象限,是直线上的一点,若是等腰直角三角形,且,求点的坐标,
19.如图所示,根据图中信息.
(1)点P的坐标为 .
(2)当时,x的取值范围是多少?
(3)求.
20.如图,平面直角坐标系中,,,A、C分别在x轴的正、负半轴上.过点C的直线绕点C旋转,交y轴于点D,交线段于点E.
(1)直接写出A、C的坐标;
(2)写出直线的解析式;
(3)若与的面积相等,求点E的坐标.
21.【概念学习】
对于平面直角坐标系中的图形K和图形W,给出如下定义:R,S分别为图形K和图形W上任意一点,将R,S两点间距离的最小值称为图形K和图形W之间的“关联距离”,记作.例如,如图1,点与y轴之间的“关联距离”.
【理解概念】
(1)如图1,点在边长为5的正方形内,则d(T,正方形)=________;
【深入探索】
(2)如图2,一次函数图象与y轴交于点E,与x轴交于点F,若点和一次函数的图象之间的“关联距离”,求m的值;
(3)如图3,在等边中,点A的坐标是,点B,C在y轴上,点H是x轴上一点,若,请直接写出点H的坐标.
【拓展延伸】
(4)在中,,,,当时,对于每一个n,若和一次函数(k是常数,)的图象之间的“关联距离”,请直接写出k的取值范围.
《一次函数检测卷-2025年中考数学专项复习》参考答案
题号 1 2 3 4 5 6
答案 C A B D D B
1.C
【分析】本题考查了一次函数的定义,熟练掌握一次函数的定义是解题的关键;根据一次函数的定义条件进行逐一分析即可.
【详解】解:A.函数其形式为(为常数,) ,不符合一次函数(,为常数,)的形式,故该选项不符合题意;
B.函数是其自变量的最高次数是 ,不符合一次函数自变量最高次数为的要求,故该选项不符合题意;
C.函数可变形为 ,符合一次函数(,,)的形式,故该选项符合题意;
D.函数是常数函数,无论取何值,的值恒为 ,不符合一次函数的形式,故该选项不符合题意;
故选:C.
2.A
【分析】本题考查一次函数与一元一次不等式,根据一次函数的图象,进行求解即可.
【详解】解:由图象可知,随的增大而减小,当时,,
∴当时,的取值范围是;
故选A.
3.B
【分析】本题考查了一次函数图像与一元一次方程的关系,熟练运用数形结合思想是解题的关键.
【详解】解:∵在的图象上,
∴方程的解是
故选:B.
4.D
【分析】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,路程、速度、时间三者之间的关系.A、B、根据题意,结合图象列式计算即可;C、设乙t小时追上甲,根据甲行驶的路程=乙行驶的路程,列出方程解答便可;D、利用待定系数法分别求出时,,时函数关系式,再列方程解答即可.
【详解】解:甲车的速度为,故选项A正确,不符合题意;
乙前面的速度为:,
乙后来的速度为:,
,
则B、C两地之间的距离为,故选项B正确,不符合题意;
设乙t小时追上甲,
根据题意得,
解得,
则出发后乙追上甲,故选项C正确,不符合题意;
当时,两车距离小于40,
①当时,
设甲距离A地的距离与出发时间之间的关系式为,
代入可得,
,
,解得;
②当时,
由(1)可得,A、B两地之间的距离为:,
设乙与A地距离与出发时间x之间的函数关系式为,
代入和,
得,解得:,
,
解方程得(不合题意,舍去),
解方程得;
③当时,
解方程得,
当两车相距40千米时,甲车行驶了或或,故选项D错误,不符合题意.
故选:D.
5.D
【分析】本题考查了正比例函数图象的性质,掌握函数图象的性质是解题的关键.
根据正比例函数图象的性质即可求解.
【详解】解:∵图象在第二、四象限,
∴,
∵,图象在第一、三象限,,,
∵直线在第一、三象限越陡,则越大,
∴,
∴,
故选:.
6.B
【分析】本题考查的是一次函数的平移,反比例函数的图象与性质,反比例函数比例系数k的几何意义;先求解反比例函数为:,正比例函数为,直线为,,再进一步求解即可.
【详解】解:∵反比例函数的图象与正比例函数的图象交于点,
∴,,
解得:,
∴反比例函数为:,正比例函数为,
∵将正比例函数的图象向上平移n个单位长度后,得到的直线与反比例函数的图象交于点,
∴,即,一次函数为,
∴,
解得:,
∴直线为,
当时,,
∴,
如图,过作轴于,作轴于,过作轴于,
∴五边形的面积为,
∴四边形的面积为;
故选:B.
7.3
【分析】本题主要考查了一次函数图象的平移问题,求一次函数解析式,设将直线向上平移m个单位后得到的直线经过点,则平移后的直线解析式为,据此利用待定系数法求解即可.
【详解】解:设将直线向上平移m个单位后得到的直线经过点,
∴平移后的直线解析式为,
∴,
∴,
故答案为:3.
8.2
【分析】本题考查的是正比例函数的定义,熟知正比例函数的定义是解答此题的关键.
一般地,形如(k是常数,)的函数叫做正比例函数,其中k叫做比例系数,据此解答即可.
【详解】解:∵函数是正比例函数,
∴,且,
∴.
故答案为:2.
9.
【分析】本题主要考查了一次函数与二元一次方程组的知识,依据题意,两个函数图象的交点横坐标为2,则可得纵坐标为2,又方程组的解就是两个函数图象交点的横坐标与纵坐标的值,进而可以得解.
【详解】解:由题意,∵一次函数与的图象的交点的横坐标是2,
∴交点的纵坐标为,
则方程组的解为,
故答案为:.
10.12
【分析】此题考查平移的性质及一次函数的综合应用,二次根式的乘法运算,解决本题的关键是明确线段扫过的面积的计算.根据题意,线段扫过的面积的四边形面积,其高是的长,底是点平移的路程.求当点落在直线上时的横坐标即可.
【详解】解:如图所示.
点的坐标分别是和,
∴.
,,
∴由勾股定理可得:.
∴.
点在直线上,
,解得.
即.
∴.
.
即线段扫过的面积为12.
故答案为:.
11.
【分析】本题考查了解直角三角形,一次函数解析式,过点作于点F,先证明,根据,得到,利用正切的定义结合点是的中点,求出,设,求出直线的解析式,代入直线的解析式,即可求解.
【详解】解:过点作于点F,
∵,,
∴,,,
∴,
∵,
∴,
∴,
∴,
∴,
∵点,点.点是的中点,
∴,
∴,
∴,
∴,
设,直线的解析式为,则
,
解得:,
∴直线的解析式为,
将代入,
则,
解得:,
∴点的横坐标是,
故答案为:.
12.
【分析】本题考查一次函数的应用.根据题意,可以写出y与x之间的函数关系式.
【详解】解:当时,,
∴y与x之间的函数关系式为:.
故答案为:.
13./
【分析】本题考查了一次函数的应用.利用待定系数法求得,再利用甲容器向乙容器注水,始终有,求得,根据题意列方程求解即可.
【详解】解:当时,,
∵开始时甲容器液面高,
∴,
又∵时,,
∴设,
将代入得,解得,
∴,
∵甲容器向乙容器注水,始终有,
∴,
∴甲容器中的液面比乙容器中的液面低时,即,
∴,
解得,
故答案为:.
14.
【分析】本题考查了一次函数的性质,正方形的性质,点坐标规律探索,熟练掌握以上知识点是解答本题的关键.
首先找到直线与轴的交点,然后根据正方形的性质确定后续点的坐标,最后总结出的坐标规律,即可解答.
【详解】解:令,解得,
,
四边形是正方形,
;
当时,,
,
当时,,
,
,
观察规律发现,,,,,
的横坐标是,
故答案为:.
15.(1),
(2)
(3)11时或13时
【分析】本题考查了一次函数的应用,正确读取信息,熟练掌握待定系数法是解题的关键.
(1)利用待定系数法解答即可.
(2)根据两人相遇前,相遇后两种情形,解方程即可.
【详解】(1)解:设,
根据题意,得,
解得,
故;
当时,,
故图象交点的坐标为,
设,根据题意,
得,
解得,
∴,
(2)解:∴,
解得,
∴,
则,
故乙到达A地时,甲距B地的距离为.
(3)解:设经过,甲、乙相距90千米,
①甲乙相遇前,
根据题意,得则,
解得(小时),此时为11时.
②甲乙相遇后,
根据题意,得则,
解得(小时),此时为13时.
综上:行驶过程中甲、乙二人在11时或13时相距.
16.(1)
(2)每件服装的销售价为52元时,才能使每天的毛利润最大,最大毛利润是240元
【分析】本题主要考查二次函数的应用,求一次函数解析式,理解题意根据相等关系列出函数关系式,并熟练掌握二次函数的性质是解题的关键.
(1)首先利用待定系数法求出,然后表示出y即可;
(2)根据二次函数的性质求解即可.
【详解】(1)解:设每天的销量t(件)与每件的销售价x(元)之间的函数关系式为
根据题意得,
解得
∴
∴;
(2)∵
∴对称轴为直线
∵
∴抛物线开口向下
∴当时,y随x的增大而增大
∵受市场影响,服装的定价不能超过52元
∴当时,y取得最大值,最大值为
∴每件服装的销售价为52元时,才能使每天的毛利润最大,最大毛利润是240元.
17.(1);
(2);
(3).
【分析】本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式.
(1)先设出函数解析式,然后根据图象中数据,即可求得该函数的解析式;
(2)根据图象中的数据,可以求得甲的速度,然后即可计算出甲从A点追赶乙,经过走的路程;
(3)将代入(1)中的函数解析式求出相应的y的值,然后根据(2)中甲的速度,可以求出加速后的速度,最后即可计算出提速后甲追上乙还需要多少秒.
【详解】(1)解:设甲、乙两人之间的距离与追赶的时间之间的函数关系式为,
∵点,在该函数图象上,
∴,
解得,
即甲、乙两人之间的距离与追赶的时间之间的函数关系式为;
(2)解:甲的速度为:(),
则甲从A点追赶乙,经过,甲走的路程为:(米),
答:甲从A点追赶乙,经过,甲前行了272米;
(3)解:将代入,得,
设甲提速后,追上乙需要m秒,
(秒),
答:甲追赶10s后,甲、乙相距72米,若此时甲速度增加,提速后甲追上乙还需要24秒.
18.(1)见详解(2)(3)或.
【分析】本题考查了一次函数与几何图形综合,三角形全等等知识,解决问题的关键是构造全等模型.
(1)由,得,进而得证;
(2)先求出的坐标,过点C作轴于点H,先证明,再求出点C的坐标,进而利用待定系数法求的解析式即可.
(3)作于,于,构造模型,设点,,,得进而得出点.
【详解】解:(1)∵,,
,
,
,
,
,
又,
;
(2)令,则,令,则,
则点A、B的坐标分别为∶、,
过点C作轴于点H,
∵,,
∴
又∵,
∴,
∴,,
则点,
设的解析式为:,
把,代入,
则
解得∶
故直线的表达式为∶
(3)如图3,
作于,于,
设点,
,
,
由上知,,
,
当时,
当时,,,
,
点和重合,
.
综上所述,或.
19.(1)
(2)
(3)4
【分析】本题主要考查了一次函数的性质、一次函数与二元一次方程组、坐标与图形等知识点,掌握一次函数与二元一次方程组的关系是解答本题的关键.
(1)把代入可计算出m的值,把代入可求出n的值,联立两解析式所组成的方程组即可得到P点坐标;
(2)观察函数图像得到,当x大于P点的横坐标时,,据此即可解答.
(3)直接根据坐标与图形和三角形面积公式列式计算即可.
【详解】(1)解:把代入中得,解得,
∴,
把代入得,解得,
∴,
联立,解得,
∴;
(2)解:由函数图象可得,当时,;
(3)解:令,则,则,即,
∴,
∴.
20.(1)、
(2)
(3)
【分析】本题考查了待定系数法求一次函数的解析式,坐标与图形的性质,三角形的面积等知识点,数形结合是解此题的关键.
(1)根据,求解即可;
(2)用待定系数法即可求出直线的解析式;
(3)推出和的面积相等,根据面积公式求出E的纵坐标.
【详解】(1)解:∵,,
∴,
∴,;
(2)解:设直线的解析式为.
∴
解得
∴直线的解析式为;
(3)解:∵,
∴,
即,
∵点E在线段上,
∴点E在第一象限,且,
∴
∴
把代入直线的解析式得:
∴
∴.
21.(1)2;(2)m的值为或;(3),,;(4)且
【分析】(1)根据“关联距离”的定义求解即可;
(2)根据题意得点在直线l即上,过点G作,连接,结合图形,利用勾股定理及等面积法求解即可得出结果;
(3)分三种情况画出图形:当H在右侧时,当H在线段上时,当H在左侧时,作出相应图形求解即可;
(4)根据题意得出直线过定点,作出,确定当时,平移到,然后结合图形即可求解.
【详解】解:(1)与边长为5的正方形的边上的点的最小距离为2,
根据“关联距离”的定义得:d(T,正方形),
故答案为:2;
(2)根据题意得点在直线l即上,
过点G作,连接,如图所示:
∵,
当时,,当时,,
∴,
∴,
∵,
∴,
∴
解得:,
∴;
当时,
解得:
∴,结合图形得:
点与点G关于点C对称,
∴,
∴;
综上可得或,
即m的值为或;
(2)当H在右侧时,如图:
,
,
的坐标是,
的坐标是;
当H在线段上时,过H作于D,如图:
,
,
是等边三角形,,
,
,
的坐标是,
,
的坐标是;
当H在左侧时,如图:
,
,
;
综上所述,H的坐标为或或;
(3)
当时,,
直线过定点,
当时,,,,
当时,,,,
做出相应图形为:
当时,平移到,
把代入得:,
解得,
把代入得:,
解得,
∴结合图形得,
∴且.
【点睛】本题考查一次函数的综合应用,涉及新定义,等边三角形,平行四边形等知识,解题的关键是分类讨论思想和数形结合思想的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
