期中达标测试卷(含解析)-2024-2025学年数学七年级下册北师大版(2024)
文档属性
| 名称 | 期中达标测试卷(含解析)-2024-2025学年数学七年级下册北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 719.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 20:21:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中达标测试卷-2024-2025学年数学七年级下册北师大版(2024)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
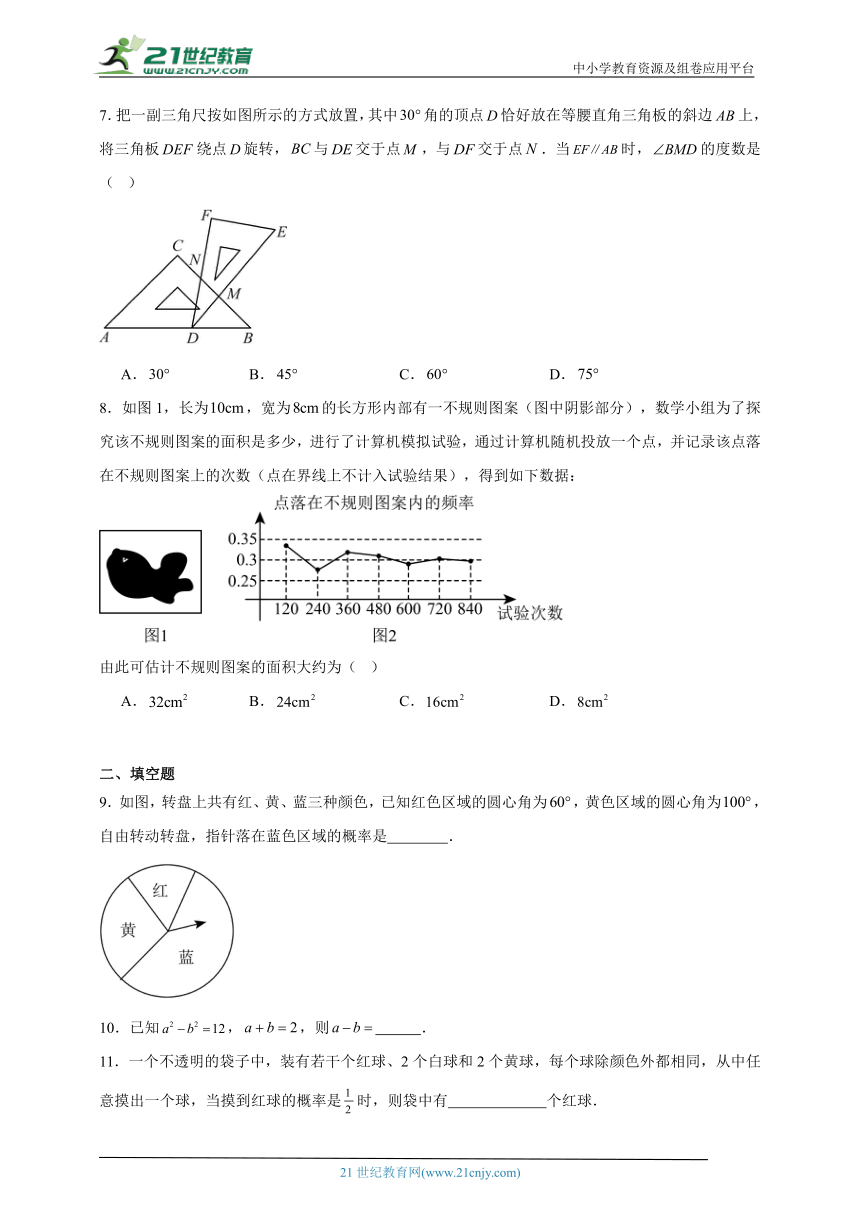
1.下列成语描述的事件为随机事件的是( )
A.水涨船高 B.水中捞月 C.守株待兔 D.缘木求鱼
2.下列计算不正确的是( )
A. B.
C. D.
3.下列各图中,∠1和∠2 不是同位角的是( )
A. B. C. D.
4.若,,,则,,的大小关系是( )
A. B. C. D.
5.下列各式,能用平方差公式计算的是( )
A. B.
C. D.
6.如图,长方形纸片沿折叠,A,D两点分别与对应,若,则的度数为( )
A. B. C. D.
7.把一副三角尺按如图所示的方式放置,其中角的顶点恰好放在等腰直角三角板的斜边上,将三角板绕点旋转,与交于点,与交于点.当时,的度数是( )
A. B. C. D.
8.如图1,长为,宽为的长方形内部有一不规则图案(图中阴影部分),数学小组为了探究该不规则图案的面积是多少,进行了计算机模拟试验,通过计算机随机投放一个点,并记录该点落在不规则图案上的次数(点在界线上不计入试验结果),得到如下数据:
由此可估计不规则图案的面积大约为( )
A. B. C. D.
二、填空题
9.如图,转盘上共有红、黄、蓝三种颜色,已知红色区域的圆心角为,黄色区域的圆心角为,自由转动转盘,指针落在蓝色区域的概率是 .
10.已知,,则 .
11.一个不透明的袋子中,装有若干个红球、2个白球和2个黄球,每个球除颜色外都相同,从中任意摸出一个球,当摸到红球的概率是时,则袋中有 个红球.
12.如图,于点,于点,已知,,则点到直线的距离是 .
13.计算的结果是 .
14.如图,两个正方形边长分别为a,b,如果,则阴影部分的面积为 .
15.如图,,,,则的度数为 .
三、解答题
16.计算:
(1)
(2)
17.先化简,再求值:,其中.
18.如图,直线相交于点,平分.若,求的度数.
19.在一个不透明的口袋中装有个红球,个白球,这个球除颜色外其他完全相同
(1)从口袋中随机摸出个球,请写出在这一过程中的一个必然事件和一个不可能事件;
(2)若从口袋中随机摸出个球,试求摸到红球的概率;
(3)若再往不透明的口袋中装入若干个黑球,它们除颜色外其他完全相同,从中摸出个球.通过多次摸球试验发现,摸到红球的频率稳定在附近,求口袋中黑球大约有多少个.
20.完成下列证明:
如图1,在四边形中.点为延长线上一点,点为延长线上一点,连接,交于点,交于点,若,.求证:.
证明:(已知),(_______)
_______(_______).
(_______).
________(_______).
(已知).
(_______).
_______(_______).
(_______).
21.如图①,从边长为的大正方形中剪掉一个边长为的小正方形,将阴影部分沿虚线剪开,拼成如图②所示的长方形.比较两图的阴影部分面积,可以得到乘法公式:________(用字母,表示);
请应用这个公式完成下列各题:
①已知,,则的值为________;
②计算:;
③计算:.
22.综合与实践
动手操作可提高我们的思维能力,白老师和同学们利用两块直角三角板(含的直角三角板和含的直角三角板)不同的摆放方式探究平行线的相关问题.
初步认知
(1)如图1,将三角板直角顶点与重合,若,求的度数.
深入探究
白老师让同学们改变三角板的位置,提出新的问题并作出解答.
(2)①“智慧小组”提出问题:如图2,将三角板的顶点放在三角板的边上,若,求证:平分.
②“善思小组”提出问题:将两块直角三角板按如图3所示的方式摆放,若,,求的度数.
《期中达标测试卷-2024-2025学年数学七年级下册北师大版(2024)》参考答案
题号 1 2 3 4 5 6 7 8
答案 C C D D D D D B
1.C
【分析】根据事件发生的可能性大小判断.本题考查了随机事件,解决本题需要正确理解必然事件,不可能事件,随机事件的概念.必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:A、水涨船高,是必然事件,不符合题意;
B、水中捞月,是不可能事件,不符合题意;
C、守株待兔,是随机事件,符合题意;
D、缘木求鱼,是不可能事件,不符合题意;
故选:C.
2.C
【分析】本题考查合并同类项法则、积的乘方、幂的乘方、同底数幂的乘法,熟练掌握相关运算法则是解题的关键.
根据积的乘方、同底数幂的乘法、合并同类项法则、幂的乘方法则进行计算即可.
【详解】解:A、,故选项计算正确,不符合题意;
B、,,故选项计算正确,不符合题意;
C、,故选项计算不正确,符合题意;
D、,故选项计算正确,不符合题意;
故选:C.
3.D
【分析】本题考查了同位角,熟练掌握同位角的特征是解题的关键.根据同位角的特征逐一判断即可.
【详解】解:A.与有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意
B. 与有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
C. 与有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D. 与的一边不在同一条直线上,不是同位角,符合题意.
故选:.
4.D
【分析】本题考查零指数幂,平方差公式,积的乘方,先分别计算a,b,c的值,再比较即可.
【详解】解:,
,,
因为,
所以,
故选:D.
5.D
【分析】本题考查了平方差公式,平方差公式为 ,需满足两数之和与两数之差的乘积.
根据平方差公式的结构特征判断即可.
【详解】解:A、,不能用平方差公式计算,不符合题意;
B、,不能用平方差公式计算,不符合题意;
C、,不能用平方差公式计算,不符合题意;
D、,能用平方差公式计算,符合题意,
故选:D.
6.D
【分析】本题考查平行线的性质,与角平分线有关的计算,根据平行线的性质,折叠的性质推出,利用平角的定义进行求解即可.
【详解】解:∵长方形纸片
∴,
∴,
由折叠的性质得出,
∵,
∴,
∵,
∴,
∴.
∴.
故选:D.
7.D
【分析】本题考查了平行线的性质,三角形内角和定理.利用平行线的性质求得,再利用三角形内角和定理即可求解.
【详解】解:∵,,
∴,
∵,
∴,
故选:D.
8.B
【分析】本题考查了几何概率以及用频率估计概率,并在此基础上进行了题目创新,关键在于读懂折线统计图的含义,随着实验次数的增加,频率稳定于附近,由此得实验的频率,并把它作为概率.这对学生知识的灵活应用提出了更高的要求.根据折线统计图知,当实验的次数逐渐增加时,样本的频率稳定在,因此用频率估计概率,再根据几何概率知,不规则图案的面积与矩形面积的比为,即可求得不规则图案的面积.
【详解】解:由折线统计图知,随着实验次数的增加,小球落在不规则图案上的频率稳定在,于是把作为概率.
设不规则图案的面积为,则有
解得:,
即不规则图案的面积为.
故选:B.
9.
【分析】本题主要考查了几何概率的计算方法,在解题时能够计算出蓝色区域对应的圆心角是本题的关键.
【详解】解:P(指针落在蓝色区域),
故答案为:.
10.
【分析】本题考查了平方差公式,掌握平方差公式是解题的关键.根据平方差公式进行计算即可.
【详解】解:∵,,,
∴,
故答案为:.
11.4
【分析】本题考查了概率公式,设有x个红球,根据题意列方程即可,熟知概率的计算方法是解答此题的关键.
【详解】解:设有x个红球,根据题意,
得,
解得,即袋子中有4个红球.
故答案为:4.
12.
【分析】本题考查了点到直线的距离,熟记点到直线的距离的定义是解题的关键.
根据点到直线的距离的定义解答即可.
【详解】解:,,
点到直线的距离是,
故答案为:.
13./
【分析】本题考查了平方差公式化简计算,掌握是解题的关键.
从后往前连续使用平方差公式求解即可.
【详解】解:
,
故答案为:.
14.9
【分析】本题考查了完全平方式的变形,以及阴影部分面积的表示方法,用a和b表示出阴影部分面积,再通过完全平方公式的变换,可求出阴影部分面积.
【详解】解:∵两个正方形边长分别为a,b,
∴,
∴, ,,
∴
,
∵,
∴,
∴,
∴,
∴S阴影.
故答案为:9
15./80度
【分析】本题考查平行线的判定及性质,由得到,从而,进而有,根据平行线的性质即可解答.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴.
故答案为:
16.(1)
(2)
【分析】本题主要考查了整式的运算.
(1)先计算积的乘方和同底数幂乘法,再合并同类项计算即可;
(2)利用多项式乘单项式法则计算即可.
【详解】(1)解:
(2)
17.;.
【分析】本题考查了整式的化简求值,做法是先把代数式化简,然后再代入求值.
先利用完全平方公式和平方差公式化简,再合并同类项,然后代入求值.
【详解】解:
当时,.
18.
【分析】本题考查了邻补角的性质,角平分线的定义,对顶角的性质,设,则,可得,进而可得,即可由角平分线的定义得,最后根据对顶角的性质即可求解,掌握以上知识点是解题的关键.
【详解】解:设,则,
∵,
∴,
∴,
∴,
∵平分,
∴,
∴.
19.(1)必然事件:从口袋中随机摸出个球,至少有个是红球;不可能事件:从口袋中随机摸出个球,都是白球(答案不唯一);
(2);
(3)个.
【分析】本题主要考查了随机事件、必然事件、不可能事件.随机事件可能发生也可能不发生的事件;必然事件是一定会发生的事件;不可能事件是不会发生的事件.
根据必然事件和不可能事件的定义写出一个必然事件和一个可能事件即可;
口袋中有个白球和个红球,从口袋中随机摸出一个球共有种等可能的情况,其中是红球的情况有种,所以随机摸出个红球的概率是;
通过多次摸球试验发现,摸到红球的频率稳定在附近,说明口袋中红球的数量占小球总数的,设口袋中黑球约有个,可以列出关于的一元一次方程,解方程求出的值即可.
【详解】(1)解:必然事件:从口袋中随机摸出个球,至少有个是红球;
不可能事件:从口袋中随机摸出个球,都是白球;
(2)解:从口袋中随机摸出一个球共有种等可能的情况,其中是红球的情况有种,
随机摸出个红球的概率是;
(3)解:设口袋中黑球约有个,
根据题意可得:,
解得:,
口袋中黑球大约有个.
20.见解析
【分析】此题考查了平行线的判定与性质,以及对顶角相等,解题的关键是掌握平行线的判定与性质.根据平行线的判定与性质求解即可.
【详解】证明:(已知),(对顶角相等)
(等量代换).
(同位角相等,两直线平行).
(两直线平行同旁内角互补).
(已知).
(等量代换).
(同旁内角互补,两直线平行).
(两直线平行,内错角相等).
21.(1);(2)①12;②;③
【分析】本题考查了平方差公式,利用平方差公式解决问题.
(1)利用两个面积相等列式即可;
(2)①利用平方差公式计算即可;②利用平方差公式计算即可;③算式乘以,再利用平方差公式计算即可.
【详解】解:(1)图①中的阴影面积为;图②的面积为;
这两个面积相等,所以,
故答案为:.
(2)①根据平方差公式可得:;
因为,,
所以
故答案为:12;
②原式;
③原式
,
.
22.(1);(2)①见解析;②
【分析】本题考查了平行线的性质,熟练掌握平行线的性质是解答本题的关键.
(1)先根据两直线平行,内错角相等求出,进而可求出的度数;
(2)①先根据两直线平行,内错角相等求出,进而可求出平分;
②先根据两直线平行,同位角相等求出,进而可求出的度数,然后再根据两直线平行,同位角相等即可求解.
【详解】(1)解:∵,,
∴,
∵,
∴;
(2)①证明:∵,,
∴,
∵,
∴,
∴平分;
②解:∵,,
∴,
∵
∴,
∴,
∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中达标测试卷-2024-2025学年数学七年级下册北师大版(2024)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列成语描述的事件为随机事件的是( )
A.水涨船高 B.水中捞月 C.守株待兔 D.缘木求鱼
2.下列计算不正确的是( )
A. B.
C. D.
3.下列各图中,∠1和∠2 不是同位角的是( )
A. B. C. D.
4.若,,,则,,的大小关系是( )
A. B. C. D.
5.下列各式,能用平方差公式计算的是( )
A. B.
C. D.
6.如图,长方形纸片沿折叠,A,D两点分别与对应,若,则的度数为( )
A. B. C. D.
7.把一副三角尺按如图所示的方式放置,其中角的顶点恰好放在等腰直角三角板的斜边上,将三角板绕点旋转,与交于点,与交于点.当时,的度数是( )
A. B. C. D.
8.如图1,长为,宽为的长方形内部有一不规则图案(图中阴影部分),数学小组为了探究该不规则图案的面积是多少,进行了计算机模拟试验,通过计算机随机投放一个点,并记录该点落在不规则图案上的次数(点在界线上不计入试验结果),得到如下数据:
由此可估计不规则图案的面积大约为( )
A. B. C. D.
二、填空题
9.如图,转盘上共有红、黄、蓝三种颜色,已知红色区域的圆心角为,黄色区域的圆心角为,自由转动转盘,指针落在蓝色区域的概率是 .
10.已知,,则 .
11.一个不透明的袋子中,装有若干个红球、2个白球和2个黄球,每个球除颜色外都相同,从中任意摸出一个球,当摸到红球的概率是时,则袋中有 个红球.
12.如图,于点,于点,已知,,则点到直线的距离是 .
13.计算的结果是 .
14.如图,两个正方形边长分别为a,b,如果,则阴影部分的面积为 .
15.如图,,,,则的度数为 .
三、解答题
16.计算:
(1)
(2)
17.先化简,再求值:,其中.
18.如图,直线相交于点,平分.若,求的度数.
19.在一个不透明的口袋中装有个红球,个白球,这个球除颜色外其他完全相同
(1)从口袋中随机摸出个球,请写出在这一过程中的一个必然事件和一个不可能事件;
(2)若从口袋中随机摸出个球,试求摸到红球的概率;
(3)若再往不透明的口袋中装入若干个黑球,它们除颜色外其他完全相同,从中摸出个球.通过多次摸球试验发现,摸到红球的频率稳定在附近,求口袋中黑球大约有多少个.
20.完成下列证明:
如图1,在四边形中.点为延长线上一点,点为延长线上一点,连接,交于点,交于点,若,.求证:.
证明:(已知),(_______)
_______(_______).
(_______).
________(_______).
(已知).
(_______).
_______(_______).
(_______).
21.如图①,从边长为的大正方形中剪掉一个边长为的小正方形,将阴影部分沿虚线剪开,拼成如图②所示的长方形.比较两图的阴影部分面积,可以得到乘法公式:________(用字母,表示);
请应用这个公式完成下列各题:
①已知,,则的值为________;
②计算:;
③计算:.
22.综合与实践
动手操作可提高我们的思维能力,白老师和同学们利用两块直角三角板(含的直角三角板和含的直角三角板)不同的摆放方式探究平行线的相关问题.
初步认知
(1)如图1,将三角板直角顶点与重合,若,求的度数.
深入探究
白老师让同学们改变三角板的位置,提出新的问题并作出解答.
(2)①“智慧小组”提出问题:如图2,将三角板的顶点放在三角板的边上,若,求证:平分.
②“善思小组”提出问题:将两块直角三角板按如图3所示的方式摆放,若,,求的度数.
《期中达标测试卷-2024-2025学年数学七年级下册北师大版(2024)》参考答案
题号 1 2 3 4 5 6 7 8
答案 C C D D D D D B
1.C
【分析】根据事件发生的可能性大小判断.本题考查了随机事件,解决本题需要正确理解必然事件,不可能事件,随机事件的概念.必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:A、水涨船高,是必然事件,不符合题意;
B、水中捞月,是不可能事件,不符合题意;
C、守株待兔,是随机事件,符合题意;
D、缘木求鱼,是不可能事件,不符合题意;
故选:C.
2.C
【分析】本题考查合并同类项法则、积的乘方、幂的乘方、同底数幂的乘法,熟练掌握相关运算法则是解题的关键.
根据积的乘方、同底数幂的乘法、合并同类项法则、幂的乘方法则进行计算即可.
【详解】解:A、,故选项计算正确,不符合题意;
B、,,故选项计算正确,不符合题意;
C、,故选项计算不正确,符合题意;
D、,故选项计算正确,不符合题意;
故选:C.
3.D
【分析】本题考查了同位角,熟练掌握同位角的特征是解题的关键.根据同位角的特征逐一判断即可.
【详解】解:A.与有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意
B. 与有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
C. 与有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D. 与的一边不在同一条直线上,不是同位角,符合题意.
故选:.
4.D
【分析】本题考查零指数幂,平方差公式,积的乘方,先分别计算a,b,c的值,再比较即可.
【详解】解:,
,,
因为,
所以,
故选:D.
5.D
【分析】本题考查了平方差公式,平方差公式为 ,需满足两数之和与两数之差的乘积.
根据平方差公式的结构特征判断即可.
【详解】解:A、,不能用平方差公式计算,不符合题意;
B、,不能用平方差公式计算,不符合题意;
C、,不能用平方差公式计算,不符合题意;
D、,能用平方差公式计算,符合题意,
故选:D.
6.D
【分析】本题考查平行线的性质,与角平分线有关的计算,根据平行线的性质,折叠的性质推出,利用平角的定义进行求解即可.
【详解】解:∵长方形纸片
∴,
∴,
由折叠的性质得出,
∵,
∴,
∵,
∴,
∴.
∴.
故选:D.
7.D
【分析】本题考查了平行线的性质,三角形内角和定理.利用平行线的性质求得,再利用三角形内角和定理即可求解.
【详解】解:∵,,
∴,
∵,
∴,
故选:D.
8.B
【分析】本题考查了几何概率以及用频率估计概率,并在此基础上进行了题目创新,关键在于读懂折线统计图的含义,随着实验次数的增加,频率稳定于附近,由此得实验的频率,并把它作为概率.这对学生知识的灵活应用提出了更高的要求.根据折线统计图知,当实验的次数逐渐增加时,样本的频率稳定在,因此用频率估计概率,再根据几何概率知,不规则图案的面积与矩形面积的比为,即可求得不规则图案的面积.
【详解】解:由折线统计图知,随着实验次数的增加,小球落在不规则图案上的频率稳定在,于是把作为概率.
设不规则图案的面积为,则有
解得:,
即不规则图案的面积为.
故选:B.
9.
【分析】本题主要考查了几何概率的计算方法,在解题时能够计算出蓝色区域对应的圆心角是本题的关键.
【详解】解:P(指针落在蓝色区域),
故答案为:.
10.
【分析】本题考查了平方差公式,掌握平方差公式是解题的关键.根据平方差公式进行计算即可.
【详解】解:∵,,,
∴,
故答案为:.
11.4
【分析】本题考查了概率公式,设有x个红球,根据题意列方程即可,熟知概率的计算方法是解答此题的关键.
【详解】解:设有x个红球,根据题意,
得,
解得,即袋子中有4个红球.
故答案为:4.
12.
【分析】本题考查了点到直线的距离,熟记点到直线的距离的定义是解题的关键.
根据点到直线的距离的定义解答即可.
【详解】解:,,
点到直线的距离是,
故答案为:.
13./
【分析】本题考查了平方差公式化简计算,掌握是解题的关键.
从后往前连续使用平方差公式求解即可.
【详解】解:
,
故答案为:.
14.9
【分析】本题考查了完全平方式的变形,以及阴影部分面积的表示方法,用a和b表示出阴影部分面积,再通过完全平方公式的变换,可求出阴影部分面积.
【详解】解:∵两个正方形边长分别为a,b,
∴,
∴, ,,
∴
,
∵,
∴,
∴,
∴,
∴S阴影.
故答案为:9
15./80度
【分析】本题考查平行线的判定及性质,由得到,从而,进而有,根据平行线的性质即可解答.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴.
故答案为:
16.(1)
(2)
【分析】本题主要考查了整式的运算.
(1)先计算积的乘方和同底数幂乘法,再合并同类项计算即可;
(2)利用多项式乘单项式法则计算即可.
【详解】(1)解:
(2)
17.;.
【分析】本题考查了整式的化简求值,做法是先把代数式化简,然后再代入求值.
先利用完全平方公式和平方差公式化简,再合并同类项,然后代入求值.
【详解】解:
当时,.
18.
【分析】本题考查了邻补角的性质,角平分线的定义,对顶角的性质,设,则,可得,进而可得,即可由角平分线的定义得,最后根据对顶角的性质即可求解,掌握以上知识点是解题的关键.
【详解】解:设,则,
∵,
∴,
∴,
∴,
∵平分,
∴,
∴.
19.(1)必然事件:从口袋中随机摸出个球,至少有个是红球;不可能事件:从口袋中随机摸出个球,都是白球(答案不唯一);
(2);
(3)个.
【分析】本题主要考查了随机事件、必然事件、不可能事件.随机事件可能发生也可能不发生的事件;必然事件是一定会发生的事件;不可能事件是不会发生的事件.
根据必然事件和不可能事件的定义写出一个必然事件和一个可能事件即可;
口袋中有个白球和个红球,从口袋中随机摸出一个球共有种等可能的情况,其中是红球的情况有种,所以随机摸出个红球的概率是;
通过多次摸球试验发现,摸到红球的频率稳定在附近,说明口袋中红球的数量占小球总数的,设口袋中黑球约有个,可以列出关于的一元一次方程,解方程求出的值即可.
【详解】(1)解:必然事件:从口袋中随机摸出个球,至少有个是红球;
不可能事件:从口袋中随机摸出个球,都是白球;
(2)解:从口袋中随机摸出一个球共有种等可能的情况,其中是红球的情况有种,
随机摸出个红球的概率是;
(3)解:设口袋中黑球约有个,
根据题意可得:,
解得:,
口袋中黑球大约有个.
20.见解析
【分析】此题考查了平行线的判定与性质,以及对顶角相等,解题的关键是掌握平行线的判定与性质.根据平行线的判定与性质求解即可.
【详解】证明:(已知),(对顶角相等)
(等量代换).
(同位角相等,两直线平行).
(两直线平行同旁内角互补).
(已知).
(等量代换).
(同旁内角互补,两直线平行).
(两直线平行,内错角相等).
21.(1);(2)①12;②;③
【分析】本题考查了平方差公式,利用平方差公式解决问题.
(1)利用两个面积相等列式即可;
(2)①利用平方差公式计算即可;②利用平方差公式计算即可;③算式乘以,再利用平方差公式计算即可.
【详解】解:(1)图①中的阴影面积为;图②的面积为;
这两个面积相等,所以,
故答案为:.
(2)①根据平方差公式可得:;
因为,,
所以
故答案为:12;
②原式;
③原式
,
.
22.(1);(2)①见解析;②
【分析】本题考查了平行线的性质,熟练掌握平行线的性质是解答本题的关键.
(1)先根据两直线平行,内错角相等求出,进而可求出的度数;
(2)①先根据两直线平行,内错角相等求出,进而可求出平分;
②先根据两直线平行,同位角相等求出,进而可求出的度数,然后再根据两直线平行,同位角相等即可求解.
【详解】(1)解:∵,,
∴,
∵,
∴;
(2)①证明:∵,,
∴,
∵,
∴,
∴平分;
②解:∵,,
∴,
∵
∴,
∴,
∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
