2025年中考数学二轮复习 专题19几何最值问题 课件 (共47张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习 专题19几何最值问题 课件 (共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 17:44:31 | ||
图片预览







文档简介
(共47张PPT)
专题十九 几何最值问题
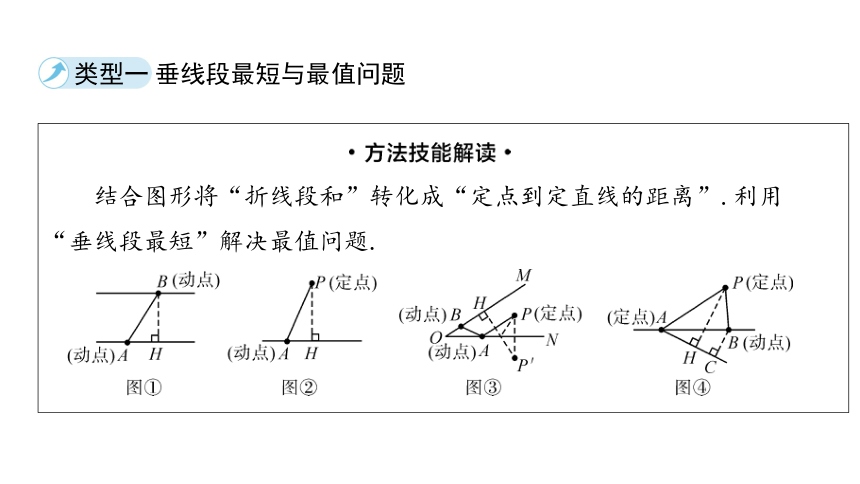
类型一 垂线段最短与最值问题
结合图形将“折线段和”转化成“定点到定直线的距离”.利用
“垂线段最短”解决最值问题.
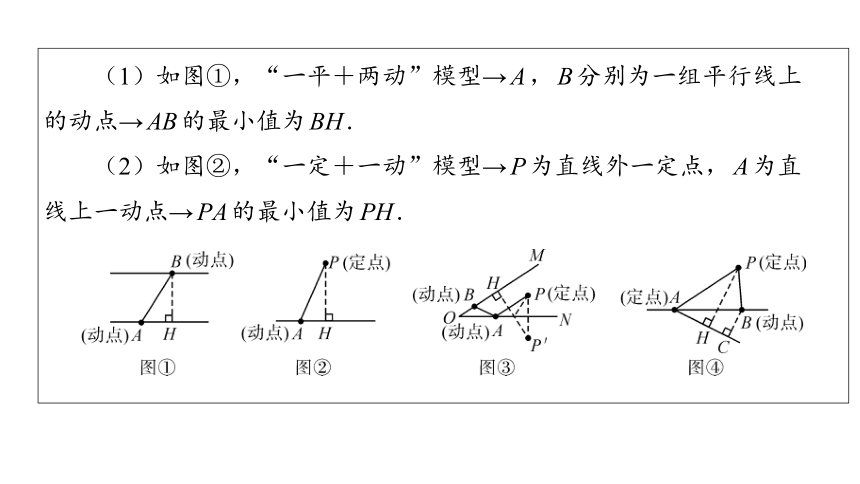
(1)如图①,“一平+两动”模型→A,B分别为一组平行线上
的动点→AB的最小值为BH.
(2)如图②,“一定+一动”模型→P为直线外一定点,A为直
线上一动点→PA的最小值为PH.
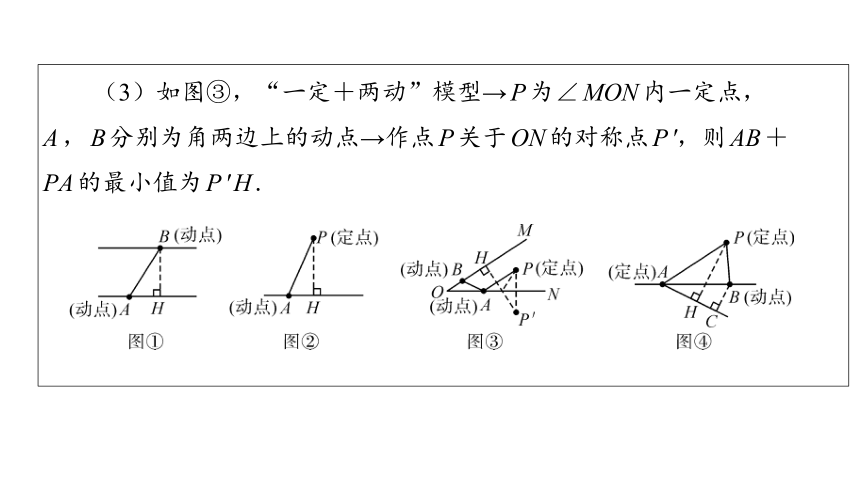
(3)如图③,“一定+两动”模型→P为∠MON内一定点,
A,B分别为角两边上的动点→作点P关于ON的对称点P',则AB+
PA的最小值为P'H.
(4)如图④,“两定+一动”模型→P为直线外一定点,A为直
线上一定点,B为直线上一动点→构造Rt△ABC( sin ∠BAC=k)
→BC=kAB→kAB+PB=PB+BC的最小值为PH.
模型一:“一平+两动”
1. 如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,P为BC边
上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接
PQ,则PQ长度的最小值为 .
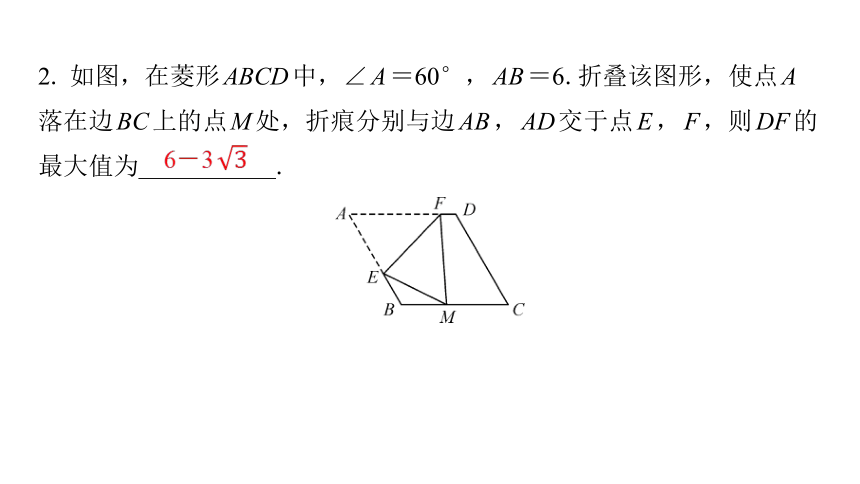
2. 如图,在菱形ABCD中,∠A=60°,AB=6.折叠该图形,使点A
落在边BC上的点M处,折痕分别与边AB,AD交于点E,F,则DF的
最大值为 .
6-3
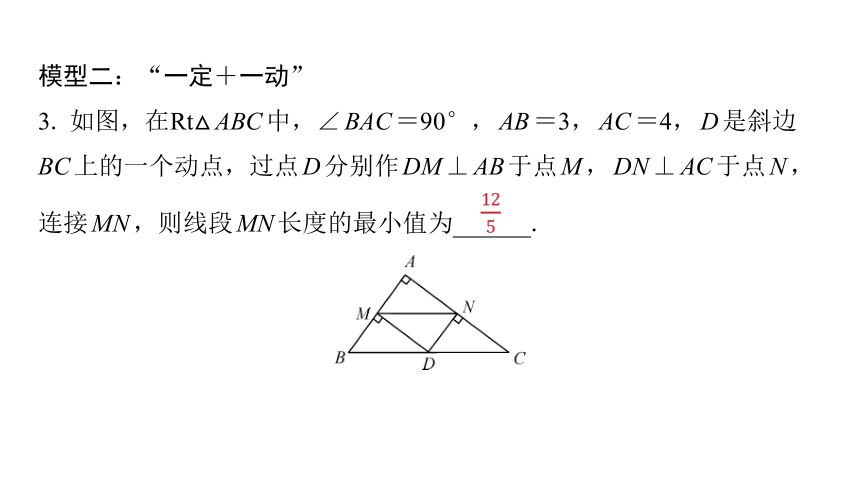
模型二:“一定+一动”
3. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D是斜边
BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,
连接MN,则线段MN长度的最小值为 .
4. 如图,在菱形ABCD中,∠ABC=60°,AB=6,E为CD边上一动
点,连接BE,F,G分别是AB,BE的中点,连接FG,则FG的最小
值为 .
模型三:“一定+两动”
5. 如图,菱形ABCD的边长为2,∠ABC=45°,P,Q分别是BC,
BD上的动点,则CQ+PQ的最小值为 .
6. 如图,在矩形ABCD中,E是AD上的一个动点,F是对角线BD上的
一个动点,连接BE,EF. 若AB=5,AD=10,则BE+EF的最小值
为 .
4
7. 如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,AE
平分∠DAC,CF=DE,连接DF分别交AE,AC于点G,M. P是AG
上的一个动点,过点P作PN⊥AC于点N,连接PM,则PM+PN的最
小值为 .
2
模型四:“两定+一动”
8. 如图,在 ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD
上的一动点,则PB+ PD的最小值为 3 .
3
9. 如图,在△ABC中,AB=5,AC=4, sin A= ,BD⊥AC于点
D,P为线段BD上一动点,则PC+ PB的最小值为 .
10. 如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),C(-
3,0)两点,与y轴交于点B(0,3).若P为y轴上一个动点,连接
AP,则 BP+AP的最小值为 2 .
2
类型二 轴对称与最值问题
结合图形将“折线段和”转化成“两个定点之间的距离”.利用
“两点之间,线段最短”解决最值问题.
(1)如图,“两定+一动”模型→作点A关于直线的对称点A',
连接A'B交直线于点P→PA+PB的最小值为A'B的长.
(2)如图,“一定+两动”模型→分别作点P关于OA,OB的对
称点P1,P2,连接P1P2分别交OA,OB于点N,M→PN+MN+PM
的最小值为P1P2的长.
(3)如图,“两定+两动”模型→作AA1平行于直线,且AA1=
MN;作A1关于直线的对称点A2,连接A2B交直线于点N→AM+NM
+BN的最小值为MN+A2B的长.
模型一:“两定+一动”
1. 如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上
的动点.若AB=3,则PE+PF的最小值是 ,此时 的值
为 .
2. 如图,在扇形AOB中,∠AOB=60°,OD平分∠AOB,交 于
点D,C是半径OB上一动点.若OA=1,则阴影部分周长的最小值
为 .
+
3. 如图,抛物线y=-x2+2x+3的顶点为A,与y轴的交点为B,P为
x轴上一动点,则当点P的坐标为 时,PA+PB取得最小
值,最小值为 .
( ,0)
5
模型二:“一定+两动”
4. 如图,在△ABC中,∠ABC=45°,P是AC上一定点,BP=6,
D,E分别是AB,BC上的动点,连接DP,EP,DE,则△PDE周长
的最小值为 .
6
5. 如图,∠AOB=30°,点M,N分别在边OA,OB上,且OM=1,
ON=3,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值
是 .
6. 如图,一次函数y=x+4的图象与x轴、y轴分别交于A,B两点,
C为OA的中点,E,F分别为直线AB和y轴上的两个动点,当△CEF
周长最小时,点E的坐标为 ,点F的坐标为 .
(- , )
(0, )
模型三:“两定+两动”
7. 如图,在矩形ABCD中,AB=4,BC=2,G是AD的中点,线段
EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 .
3
8. 如图,在矩形ABCD中,AB=5,BC=4,E,F分别是AD,BC的
中点,点P,Q在EF上,且PQ=2,则四边形APQB周长的最小值
为 .
12
9. [2024·新疆]如图,抛物线y= x2-4x+6与y轴交于点A,与x轴交
于点B,线段CD在抛物线的对称轴上移动(点C在点D下方),且CD
=3.当AD+BC的值最小时,点C的坐标为 .
(4,1)
类型三 线段差的最大值问题
(1)如图①,“同侧两定点”模型→由三角形三边关系可得
≤AB→延长AB交直线于点P'(A,B,P'共线)
→ 最大值为 =AB.
(2)如图②,“异侧两定点”模型→作点B关于直线的对称点
B'→ = →转化成“同侧两定点”模型.
1. 如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中
点,M是AD上一点,且MD=1,P是BC上一动点,则PM-PO的最
大值为 .
2. 如图,已知抛物线经过点O(0,0),A(5,5),点B为对称轴上
一点,其坐标为(2,8),P是抛物线上的动点,则当点P的坐标
为 时,PA-PB的值最大,其最大值为 .
(-2,12)
3
3. 如图,在△ABC中,AB=AC=4,∠BAC=120°,E为射线AD上
一动点,∠BAD=15°,连接BE,CE,则CE-BE的最大值
为 .
4
4. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的
中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-
PN的最大值为 .
2
类型四 隐形圆与最值问题
(1)如图①,
“定点定长隐形圆”模型
(2)如图②,
“定弦定角隐形圆”模型→
模型一:“定点定长隐形圆”
1. 如图,在矩形ABCD中,AB=3,BC=2,M是AD边的中点,N是
AB边上的动点,将△AMN沿MN所在直线折叠,得到△A'MN,连接
A'C,则A'C的最小值为 .
-1
2. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P
从点A出发沿AB方向运动,到达B点时停止运动.连接CP,点A关于直
线CP的对称点为A',连接A'C,A'P. 在运动过程中,点A'到直线AB
距离的最大值是 ,点P到达点B时,线段A'P扫过的面积
为 .
(1+ )π-1-
3. 如图,在正方形ABCD中,AB=4,M是边CD的中点,P是正方形
内一点,且MP=1,将线段BP以B为中心逆时针旋转90°得到线段
BQ,连接MQ,则MQ的最小值为 .
2 -1
模型二:“定弦定角隐形圆”
4. 如图,动点M在边长为2 的正方形ABCD内,且AM⊥BM,P是CD
边上的一个动点,E是AD边的中点,则线段PE+PM的最小值
是 .
-1
5. 如图,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上
一点,连接DE和AF交于点G,连接BG. 若AE=BF,则BG的最小值
是 .
-1
6. 如图,在菱形ABCD中,AB=6,∠BAD=120°,E,F分别是
AB,BC上的动点,且AE=BF,连接AF,CE相交于点P,则四边形
APCD面积的最大值为 .
12
类型五 阿氏圆与最值问题
如图,☉O的半径为r,A,B为☉O外两定点,r=OP=k·OA(0<
k<1),P为☉O上一动点,求kAP+BP的最小值.作OC=k·OP,
则 = =k,∠POC=∠AOP→△POC∽△AOP→PC=
kAP→kAP+BP=PC+BP→当B,P,C三点共线时,kAP+BP的
最小值为BC的长.
1. 如图,在Rt△ABC中,∠A=90°,AB=AC=4,E,F分别是
AB,AC的中点,P是扇形AEF的 上一动点,连接BP,CP,则
BP+CP的最小值是 .
2. 如图,已知正方形ABCD的边长为4,☉B 的半径为2,P是☉B上的
一个动点,则PD- PC的最大值是 .
5
3. 如图,☉O为正方形ABCD的内切圆,P为☉O上一动点.若AB=4,
则 PA+PB的最小值为 2 .
2
4. 如图,抛物线y=x2-6x+5与x轴交于A,B两点,与y轴交于点
C,以B为圆心,画半径为2的圆,P为☉B上一个动点,则PC+ PA
的最小值为 .
谢谢观看
专题十九 几何最值问题
类型一 垂线段最短与最值问题
结合图形将“折线段和”转化成“定点到定直线的距离”.利用
“垂线段最短”解决最值问题.
(1)如图①,“一平+两动”模型→A,B分别为一组平行线上
的动点→AB的最小值为BH.
(2)如图②,“一定+一动”模型→P为直线外一定点,A为直
线上一动点→PA的最小值为PH.
(3)如图③,“一定+两动”模型→P为∠MON内一定点,
A,B分别为角两边上的动点→作点P关于ON的对称点P',则AB+
PA的最小值为P'H.
(4)如图④,“两定+一动”模型→P为直线外一定点,A为直
线上一定点,B为直线上一动点→构造Rt△ABC( sin ∠BAC=k)
→BC=kAB→kAB+PB=PB+BC的最小值为PH.
模型一:“一平+两动”
1. 如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,P为BC边
上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接
PQ,则PQ长度的最小值为 .
2. 如图,在菱形ABCD中,∠A=60°,AB=6.折叠该图形,使点A
落在边BC上的点M处,折痕分别与边AB,AD交于点E,F,则DF的
最大值为 .
6-3
模型二:“一定+一动”
3. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D是斜边
BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,
连接MN,则线段MN长度的最小值为 .
4. 如图,在菱形ABCD中,∠ABC=60°,AB=6,E为CD边上一动
点,连接BE,F,G分别是AB,BE的中点,连接FG,则FG的最小
值为 .
模型三:“一定+两动”
5. 如图,菱形ABCD的边长为2,∠ABC=45°,P,Q分别是BC,
BD上的动点,则CQ+PQ的最小值为 .
6. 如图,在矩形ABCD中,E是AD上的一个动点,F是对角线BD上的
一个动点,连接BE,EF. 若AB=5,AD=10,则BE+EF的最小值
为 .
4
7. 如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,AE
平分∠DAC,CF=DE,连接DF分别交AE,AC于点G,M. P是AG
上的一个动点,过点P作PN⊥AC于点N,连接PM,则PM+PN的最
小值为 .
2
模型四:“两定+一动”
8. 如图,在 ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD
上的一动点,则PB+ PD的最小值为 3 .
3
9. 如图,在△ABC中,AB=5,AC=4, sin A= ,BD⊥AC于点
D,P为线段BD上一动点,则PC+ PB的最小值为 .
10. 如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),C(-
3,0)两点,与y轴交于点B(0,3).若P为y轴上一个动点,连接
AP,则 BP+AP的最小值为 2 .
2
类型二 轴对称与最值问题
结合图形将“折线段和”转化成“两个定点之间的距离”.利用
“两点之间,线段最短”解决最值问题.
(1)如图,“两定+一动”模型→作点A关于直线的对称点A',
连接A'B交直线于点P→PA+PB的最小值为A'B的长.
(2)如图,“一定+两动”模型→分别作点P关于OA,OB的对
称点P1,P2,连接P1P2分别交OA,OB于点N,M→PN+MN+PM
的最小值为P1P2的长.
(3)如图,“两定+两动”模型→作AA1平行于直线,且AA1=
MN;作A1关于直线的对称点A2,连接A2B交直线于点N→AM+NM
+BN的最小值为MN+A2B的长.
模型一:“两定+一动”
1. 如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上
的动点.若AB=3,则PE+PF的最小值是 ,此时 的值
为 .
2. 如图,在扇形AOB中,∠AOB=60°,OD平分∠AOB,交 于
点D,C是半径OB上一动点.若OA=1,则阴影部分周长的最小值
为 .
+
3. 如图,抛物线y=-x2+2x+3的顶点为A,与y轴的交点为B,P为
x轴上一动点,则当点P的坐标为 时,PA+PB取得最小
值,最小值为 .
( ,0)
5
模型二:“一定+两动”
4. 如图,在△ABC中,∠ABC=45°,P是AC上一定点,BP=6,
D,E分别是AB,BC上的动点,连接DP,EP,DE,则△PDE周长
的最小值为 .
6
5. 如图,∠AOB=30°,点M,N分别在边OA,OB上,且OM=1,
ON=3,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值
是 .
6. 如图,一次函数y=x+4的图象与x轴、y轴分别交于A,B两点,
C为OA的中点,E,F分别为直线AB和y轴上的两个动点,当△CEF
周长最小时,点E的坐标为 ,点F的坐标为 .
(- , )
(0, )
模型三:“两定+两动”
7. 如图,在矩形ABCD中,AB=4,BC=2,G是AD的中点,线段
EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 .
3
8. 如图,在矩形ABCD中,AB=5,BC=4,E,F分别是AD,BC的
中点,点P,Q在EF上,且PQ=2,则四边形APQB周长的最小值
为 .
12
9. [2024·新疆]如图,抛物线y= x2-4x+6与y轴交于点A,与x轴交
于点B,线段CD在抛物线的对称轴上移动(点C在点D下方),且CD
=3.当AD+BC的值最小时,点C的坐标为 .
(4,1)
类型三 线段差的最大值问题
(1)如图①,“同侧两定点”模型→由三角形三边关系可得
≤AB→延长AB交直线于点P'(A,B,P'共线)
→ 最大值为 =AB.
(2)如图②,“异侧两定点”模型→作点B关于直线的对称点
B'→ = →转化成“同侧两定点”模型.
1. 如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中
点,M是AD上一点,且MD=1,P是BC上一动点,则PM-PO的最
大值为 .
2. 如图,已知抛物线经过点O(0,0),A(5,5),点B为对称轴上
一点,其坐标为(2,8),P是抛物线上的动点,则当点P的坐标
为 时,PA-PB的值最大,其最大值为 .
(-2,12)
3
3. 如图,在△ABC中,AB=AC=4,∠BAC=120°,E为射线AD上
一动点,∠BAD=15°,连接BE,CE,则CE-BE的最大值
为 .
4
4. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的
中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-
PN的最大值为 .
2
类型四 隐形圆与最值问题
(1)如图①,
“定点定长隐形圆”模型
(2)如图②,
“定弦定角隐形圆”模型→
模型一:“定点定长隐形圆”
1. 如图,在矩形ABCD中,AB=3,BC=2,M是AD边的中点,N是
AB边上的动点,将△AMN沿MN所在直线折叠,得到△A'MN,连接
A'C,则A'C的最小值为 .
-1
2. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P
从点A出发沿AB方向运动,到达B点时停止运动.连接CP,点A关于直
线CP的对称点为A',连接A'C,A'P. 在运动过程中,点A'到直线AB
距离的最大值是 ,点P到达点B时,线段A'P扫过的面积
为 .
(1+ )π-1-
3. 如图,在正方形ABCD中,AB=4,M是边CD的中点,P是正方形
内一点,且MP=1,将线段BP以B为中心逆时针旋转90°得到线段
BQ,连接MQ,则MQ的最小值为 .
2 -1
模型二:“定弦定角隐形圆”
4. 如图,动点M在边长为2 的正方形ABCD内,且AM⊥BM,P是CD
边上的一个动点,E是AD边的中点,则线段PE+PM的最小值
是 .
-1
5. 如图,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上
一点,连接DE和AF交于点G,连接BG. 若AE=BF,则BG的最小值
是 .
-1
6. 如图,在菱形ABCD中,AB=6,∠BAD=120°,E,F分别是
AB,BC上的动点,且AE=BF,连接AF,CE相交于点P,则四边形
APCD面积的最大值为 .
12
类型五 阿氏圆与最值问题
如图,☉O的半径为r,A,B为☉O外两定点,r=OP=k·OA(0<
k<1),P为☉O上一动点,求kAP+BP的最小值.作OC=k·OP,
则 = =k,∠POC=∠AOP→△POC∽△AOP→PC=
kAP→kAP+BP=PC+BP→当B,P,C三点共线时,kAP+BP的
最小值为BC的长.
1. 如图,在Rt△ABC中,∠A=90°,AB=AC=4,E,F分别是
AB,AC的中点,P是扇形AEF的 上一动点,连接BP,CP,则
BP+CP的最小值是 .
2. 如图,已知正方形ABCD的边长为4,☉B 的半径为2,P是☉B上的
一个动点,则PD- PC的最大值是 .
5
3. 如图,☉O为正方形ABCD的内切圆,P为☉O上一动点.若AB=4,
则 PA+PB的最小值为 2 .
2
4. 如图,抛物线y=x2-6x+5与x轴交于A,B两点,与y轴交于点
C,以B为圆心,画半径为2的圆,P为☉B上一个动点,则PC+ PA
的最小值为 .
谢谢观看
同课章节目录
