人教版九年级数学上册 25.1 随机事件与概率 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学上册 25.1 随机事件与概率 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 376.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 17:57:02 | ||
图片预览


文档简介
九年级数学上册人教版第二十五章第1节《随机事件与概率》课时练习
一、单选题
1.袋中有形状、大小、质地完全一样的3个红球和2个白球,下列说法正确的是( )
A.从中随机抽出一个球,一定是红球
B.从袋中抽出一个球后,再从袋中抽出一个球,出现红球或白球的概率一样大
C.从袋中随机抽出2个球,出现都是红球的概率为
D.从袋中抽出2个球,出现颜色不同的球的概率是
2.掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件中,是确定性事件的是( )
A.向上一面的点数是2 B.向上一面的点数是奇数
C.向上一面的点数小于3 D.向上一面的点数小于7
3.一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,则小球停留在黑色区域内的概率是( )
A. B. C. D.
4.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是( )
A. B. C. D.
5.若某随机事件发生的概率为,则该事件在一次试验中( )
A.一定不发生 B.可能发生,也可能不发生
C.一定发生 D.以上都不对
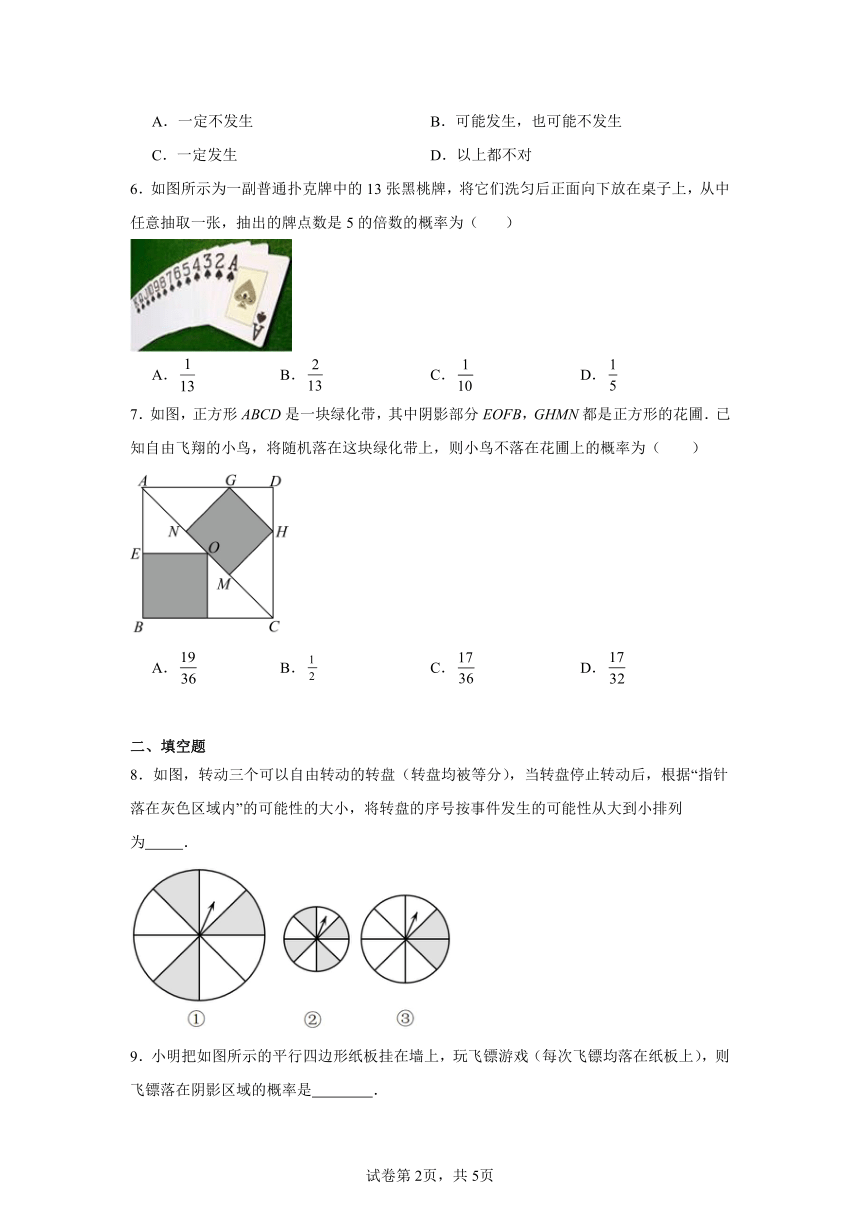
6.如图所示为一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,抽出的牌点数是5的倍数的概率为( )
A. B. C. D.
7.如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
A. B. C. D.
二、填空题
8.如图,转动三个可以自由转动的转盘(转盘均被等分),当转盘停止转动后,根据“指针落在灰色区域内”的可能性的大小,将转盘的序号按事件发生的可能性从大到小排列为 .
9.小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是 .
10.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色不同外其余都相同),其中有2个白球,1个黄球.若从中任意摸出一个球,这个球是白球的概率是,则口袋中红球有 个.
11.紫色石蕊试剂遇到酸性液体变成红色,遇到碱性液体变成蓝色,现有3瓶无标记液体,其中有两瓶酸性液体、一瓶碱性液体,现取一滴紫色石蕊试剂随机滴入一瓶试剂中,液体变为红色的概率为 .
12.在一个不透明的布袋中,红色、黑色的玻璃球共有20个,这些球除颜色外其它完全相同.将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断地重复这个过程,摸了200次后,发现有60次摸到黑球,请你估计这个袋中红球约有 个.
三、解答题
13.在甲、乙两个不透明的盒子中,分别装有除颜色外其它完全相同的小球,其中,甲盒子装有2个白球,1个红球;乙盒子装有2个红球,1个白球.
(1)将甲盒子摇匀后,随机取出一个小球,求小球是白色的概率;
(2)小华和同桌商定:将两个盒子摇匀后,各随机摸出一个小球.若颜色相同,则小华获胜;若颜色不同,则同桌获胜,请用列表法或画出树状图的方法说明谁赢的可能性大.
14.在一个不透明的袋中装有红、黄、白种颜色的球共50个,且红球比黄球多5个,它们除颜色外都相同,已知从袋中随机摸出一个球,摸到的球是白球的概率为.
(1)求原来袋中白球的个数;
(2)现从原来装有50个球的袋中随机摸出一个球,求摸到的球是红球的概率.
15.如图是芳芳设计的自由转动的转盘,上面写有10个有理数.想想看,转得下列各数的概率是多少?
(1)转得正数;
(2)转得整数;
(3)转得绝对值小于6的数.
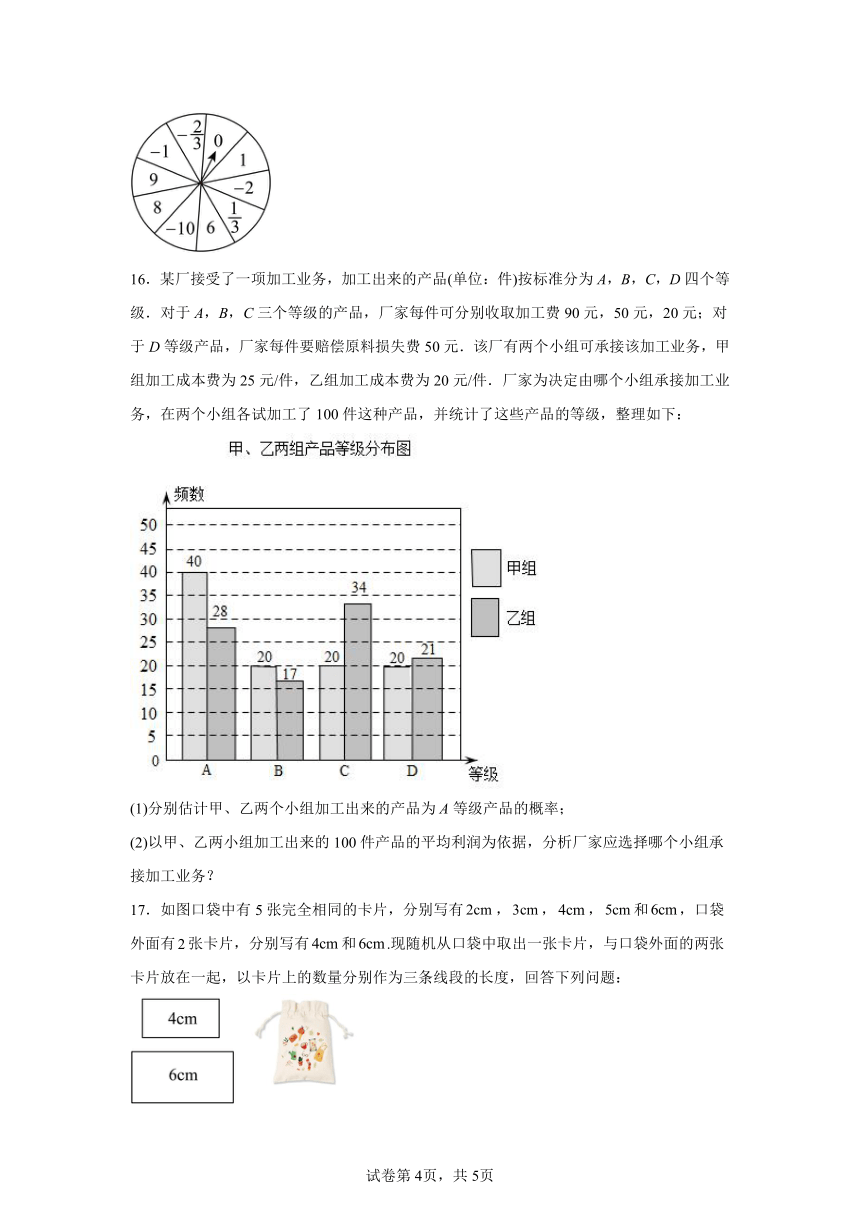
16.某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.对于A,B,C三个等级的产品,厂家每件可分别收取加工费90元,50元,20元;对于D等级产品,厂家每件要赔偿原料损失费50元.该厂有两个小组可承接该加工业务,甲组加工成本费为25元/件,乙组加工成本费为20元/件.厂家为决定由哪个小组承接加工业务,在两个小组各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
(1)分别估计甲、乙两个小组加工出来的产品为A等级产品的概率;
(2)以甲、乙两小组加工出来的100件产品的平均利润为依据,分析厂家应选择哪个小组承接加工业务?
17.如图口袋中有5张完全相同的卡片,分别写有,,,和,口袋外面有张卡片,分别写有和.现随机从口袋中取出一张卡片,与口袋外面的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,回答下列问题:
(1)根据题目要求,写出组合成的三条线度的长度的所有可能的结果;
(2)求这三条线段能组成三角形的概率;
(3)求这三条线段能组成等腰三角形的概率.
18.如图,有一个可以自由转动的均匀转盘,转盘被平均分成等份,每个扇形区域内分别标有,,,,,这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字,请回答下列问题:
(1)随机转动转盘,转出数字是______事件,转出数字是______事件;(从“随机”,“必然”,“不可能”中选一个,填空)
(2)随机转动转盘,转出的数字大于的概率是______;
(3)现有两张分别写有和的卡片,随机转动转盘,转盘停止转动后,将转出的数字与两张卡片上的数字分别作为三条线段的长度.求这三条线段能构成等腰三角形的概率.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十五章第1节《随机事件与概率》课时练习》参考答案
题号 1 2 3 4 5 6 7
答案 D D B A B B A
8.②①③
9.
10.3
11.
12.14
13.解:(1)共有3种等可能结果,而摸出白球的结果有2种
∴P(摸出白球)=
(2)根据题意,列表如下:
乙甲 红1 红2 白
白1 (白1,红1) (白1,红2) (白1,白)
白2 (白2,红1) (白2,红2) (白2,白)
红 (红,红1) (红,红2) (红,白)
由上表可知,共有9种等可能结果,其中颜色不相同的结果有5种,颜色相同的结果有4种,
∴P(颜色不相同)=,P(颜色相同)=,∵<,
∴同桌获胜获胜的可能性大.
14.解:(1)根据题意,得,
答:原来袋中白球有15个.
(2)设袋中红球有x个,则黄球有(x-5)个,根据题意,得
x+x-5+15=50,解得:x=20,
所以摸到的球是红球的概率=,
答:摸到的球是红球的概率是.
15.解:(1)∵转盘中10个数,正数有1、、6、8、9这5个,∴P(转得正数)==;
(2)∵转盘中10个数,整数有0、1、-2、6、-10、8、9、-1这8个,∴P(转得正整数)==;
(3)∵转盘中10个数,绝对值小于6的有0、1、﹣2、、﹣1、﹣这6个,∴P(转得绝对值小于6)==.
16.(1)由表可知,甲厂加工出来的一件产品为A级品的概率为0.4,
乙厂加工出来的一件产品为A级品的概率为0.28;
(2)甲小组加工出来的100件产品的平均利润为:[40×(90-25)+20×(50-25)+20×(20-25)-20×(50+25)]÷100=15(元),
乙小组加工出来的100件产品的平均利润为:[28×(90-20)+17×(50-20)+34×(20-20)-21×(50+20)]÷100=10(元),
∵15>10,
故选择甲小组承接更好.
17.(1)共有5种可能的结果数,它们是:2、4、6;3、4、6;4、4、6;5、4、6;6、4、6;
(2)这三条线段能构成一个三角形的结果数为4,
所以这三条线段能构成一个三角形的概率=;
(3)这三条线段能构成等腰三角形的结果数2,
所以这三条线段能构成等腰三角形的概率是.
18.(1)解:(1)随机转动转盘,转出数字是不可能事件,转出数字是随机事件;
故答案为:不可能;随机;
(2)随机转动转盘,共有种等可能的结果,转出的数字大于的可能结果是,,,结果数为种,
∴大于的概率为:,
故答案为:;
(3)随机转动转盘,共有种等可能的结果,其中转出的数字为或与两张卡片上的数字分别作为三条线段的长度能构成等腰三角形,结果数为种,概率为:,
∴这三条线段能构成等腰三角形的概率是.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.袋中有形状、大小、质地完全一样的3个红球和2个白球,下列说法正确的是( )
A.从中随机抽出一个球,一定是红球
B.从袋中抽出一个球后,再从袋中抽出一个球,出现红球或白球的概率一样大
C.从袋中随机抽出2个球,出现都是红球的概率为
D.从袋中抽出2个球,出现颜色不同的球的概率是
2.掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件中,是确定性事件的是( )
A.向上一面的点数是2 B.向上一面的点数是奇数
C.向上一面的点数小于3 D.向上一面的点数小于7
3.一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,则小球停留在黑色区域内的概率是( )
A. B. C. D.
4.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是( )
A. B. C. D.
5.若某随机事件发生的概率为,则该事件在一次试验中( )
A.一定不发生 B.可能发生,也可能不发生
C.一定发生 D.以上都不对
6.如图所示为一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,抽出的牌点数是5的倍数的概率为( )
A. B. C. D.
7.如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
A. B. C. D.
二、填空题
8.如图,转动三个可以自由转动的转盘(转盘均被等分),当转盘停止转动后,根据“指针落在灰色区域内”的可能性的大小,将转盘的序号按事件发生的可能性从大到小排列为 .
9.小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是 .
10.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色不同外其余都相同),其中有2个白球,1个黄球.若从中任意摸出一个球,这个球是白球的概率是,则口袋中红球有 个.
11.紫色石蕊试剂遇到酸性液体变成红色,遇到碱性液体变成蓝色,现有3瓶无标记液体,其中有两瓶酸性液体、一瓶碱性液体,现取一滴紫色石蕊试剂随机滴入一瓶试剂中,液体变为红色的概率为 .
12.在一个不透明的布袋中,红色、黑色的玻璃球共有20个,这些球除颜色外其它完全相同.将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断地重复这个过程,摸了200次后,发现有60次摸到黑球,请你估计这个袋中红球约有 个.
三、解答题
13.在甲、乙两个不透明的盒子中,分别装有除颜色外其它完全相同的小球,其中,甲盒子装有2个白球,1个红球;乙盒子装有2个红球,1个白球.
(1)将甲盒子摇匀后,随机取出一个小球,求小球是白色的概率;
(2)小华和同桌商定:将两个盒子摇匀后,各随机摸出一个小球.若颜色相同,则小华获胜;若颜色不同,则同桌获胜,请用列表法或画出树状图的方法说明谁赢的可能性大.
14.在一个不透明的袋中装有红、黄、白种颜色的球共50个,且红球比黄球多5个,它们除颜色外都相同,已知从袋中随机摸出一个球,摸到的球是白球的概率为.
(1)求原来袋中白球的个数;
(2)现从原来装有50个球的袋中随机摸出一个球,求摸到的球是红球的概率.
15.如图是芳芳设计的自由转动的转盘,上面写有10个有理数.想想看,转得下列各数的概率是多少?
(1)转得正数;
(2)转得整数;
(3)转得绝对值小于6的数.
16.某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.对于A,B,C三个等级的产品,厂家每件可分别收取加工费90元,50元,20元;对于D等级产品,厂家每件要赔偿原料损失费50元.该厂有两个小组可承接该加工业务,甲组加工成本费为25元/件,乙组加工成本费为20元/件.厂家为决定由哪个小组承接加工业务,在两个小组各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
(1)分别估计甲、乙两个小组加工出来的产品为A等级产品的概率;
(2)以甲、乙两小组加工出来的100件产品的平均利润为依据,分析厂家应选择哪个小组承接加工业务?
17.如图口袋中有5张完全相同的卡片,分别写有,,,和,口袋外面有张卡片,分别写有和.现随机从口袋中取出一张卡片,与口袋外面的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,回答下列问题:
(1)根据题目要求,写出组合成的三条线度的长度的所有可能的结果;
(2)求这三条线段能组成三角形的概率;
(3)求这三条线段能组成等腰三角形的概率.
18.如图,有一个可以自由转动的均匀转盘,转盘被平均分成等份,每个扇形区域内分别标有,,,,,这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字,请回答下列问题:
(1)随机转动转盘,转出数字是______事件,转出数字是______事件;(从“随机”,“必然”,“不可能”中选一个,填空)
(2)随机转动转盘,转出的数字大于的概率是______;
(3)现有两张分别写有和的卡片,随机转动转盘,转盘停止转动后,将转出的数字与两张卡片上的数字分别作为三条线段的长度.求这三条线段能构成等腰三角形的概率.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十五章第1节《随机事件与概率》课时练习》参考答案
题号 1 2 3 4 5 6 7
答案 D D B A B B A
8.②①③
9.
10.3
11.
12.14
13.解:(1)共有3种等可能结果,而摸出白球的结果有2种
∴P(摸出白球)=
(2)根据题意,列表如下:
乙甲 红1 红2 白
白1 (白1,红1) (白1,红2) (白1,白)
白2 (白2,红1) (白2,红2) (白2,白)
红 (红,红1) (红,红2) (红,白)
由上表可知,共有9种等可能结果,其中颜色不相同的结果有5种,颜色相同的结果有4种,
∴P(颜色不相同)=,P(颜色相同)=,∵<,
∴同桌获胜获胜的可能性大.
14.解:(1)根据题意,得,
答:原来袋中白球有15个.
(2)设袋中红球有x个,则黄球有(x-5)个,根据题意,得
x+x-5+15=50,解得:x=20,
所以摸到的球是红球的概率=,
答:摸到的球是红球的概率是.
15.解:(1)∵转盘中10个数,正数有1、、6、8、9这5个,∴P(转得正数)==;
(2)∵转盘中10个数,整数有0、1、-2、6、-10、8、9、-1这8个,∴P(转得正整数)==;
(3)∵转盘中10个数,绝对值小于6的有0、1、﹣2、、﹣1、﹣这6个,∴P(转得绝对值小于6)==.
16.(1)由表可知,甲厂加工出来的一件产品为A级品的概率为0.4,
乙厂加工出来的一件产品为A级品的概率为0.28;
(2)甲小组加工出来的100件产品的平均利润为:[40×(90-25)+20×(50-25)+20×(20-25)-20×(50+25)]÷100=15(元),
乙小组加工出来的100件产品的平均利润为:[28×(90-20)+17×(50-20)+34×(20-20)-21×(50+20)]÷100=10(元),
∵15>10,
故选择甲小组承接更好.
17.(1)共有5种可能的结果数,它们是:2、4、6;3、4、6;4、4、6;5、4、6;6、4、6;
(2)这三条线段能构成一个三角形的结果数为4,
所以这三条线段能构成一个三角形的概率=;
(3)这三条线段能构成等腰三角形的结果数2,
所以这三条线段能构成等腰三角形的概率是.
18.(1)解:(1)随机转动转盘,转出数字是不可能事件,转出数字是随机事件;
故答案为:不可能;随机;
(2)随机转动转盘,共有种等可能的结果,转出的数字大于的可能结果是,,,结果数为种,
∴大于的概率为:,
故答案为:;
(3)随机转动转盘,共有种等可能的结果,其中转出的数字为或与两张卡片上的数字分别作为三条线段的长度能构成等腰三角形,结果数为种,概率为:,
∴这三条线段能构成等腰三角形的概率是.
答案第1页,共2页
答案第1页,共2页
同课章节目录
