专题强化2.7 动量守恒定律在电磁感应中的应用 学案(含解析)
文档属性
| 名称 | 专题强化2.7 动量守恒定律在电磁感应中的应用 学案(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高中物理选择性必修二素养提升学案
第二章 电磁感应
专题强化2.7 动量守恒定律在电磁感应中的应用
【专题解读】
在两等长金属棒切割磁感线的系统中,两金属棒和水平平行金属导轨构成闭合回路,它们受到的安培力的合力为0,如果不计摩擦,它们受到的合力为0,满足动量守恒的条件,运用动量守恒定律解题比较方便.
方法点拨
双棒无外力 双棒有外力
示意图 F为恒力
动力学观点 导体棒1受安培力的作用做加速度逐渐减小的减速运动,导体棒2受安培力的作用做加速度逐渐减小的加速运动,最终两棒以相同的速度做匀速直线运动 导体棒1做加速度逐渐减小的加速运动,导体棒2做加速度逐渐增大的加速运动,最终两棒以相同的加速度做匀加速直线运动
动量观点 系统动量守恒 系统动量不守恒
能量观点 棒1动能的减少量=棒2动能的增加量+焦耳热 力F做的功=棒1的动能+棒2的动能+焦耳热
【典例剖析】
【典例】(2021福建卷)如图,P、Q是两根固定在水平面内的光滑平行金属导轨,间距为L,导轨足够长且电阻可忽略不计.图中EFHG矩形区域内有方向垂直导轨平面向上、磁感应强度大小为B的匀强磁场.在t=t1时刻,两均匀金属棒a、b分别从磁场边界EF、GH进入磁场,速度大小均为v0;一段时间后,流经a棒的电流为0,此时t=t2,b棒仍位于磁场区域内.已知金属棒a、b由相同材料制成,长度均为L,电阻分别为R和2R,a棒的质量为m.在运动过程中两金属棒始终与导轨垂直且接触良好,a、b棒没有相碰,则( AD )
A.t1时刻a棒的加速度大小为
B.t2时刻b棒的速度为0
C.t1~t2时间内,通过a棒横截面的电荷量是b棒的2倍
D.t1~t2时间内,a棒产生的焦耳热为m
解析 在t=t1时刻,两均匀金属棒a、b分别从磁场边界EF、GH进入磁场,速度大小均为v0,由右手定则可判断出两金属棒产生的感应电流方向都是逆时针方向,产生的感应电动势都是BLv0,由闭合电路欧姆定律可得,t1时刻a金属棒中的感应电流I==,受到的安培力F=BIL=,由牛顿第二定律F=ma可得,t1时刻a棒的加速度大小为a=,选项A正确;由于金属棒a、b串联构成回路,所以在t1~t2时间内,通过a棒横截面的电荷量与b棒的相同,选项C错误;由于金属棒a、b电阻分别为R和2R,金属棒a、b串联构成回路,二者电流相等,由焦耳定律可知金属棒a、b产生的焦耳热之比为1∶2,设t1~t2时间内,a棒产生的焦耳热为Q,则b棒产生的焦耳热为2Q,又两者材料相同,由电阻定律可知,金属棒a的横截面积为b的2倍,故体积为b的2倍,质量为b的2倍,即b的质量为0.5m,t=t2时刻流经a棒的电流为0,且b棒仍位于磁场区域内,说明金属棒a、b具有共同速度,由动量守恒定律有mv0-0.5mv0=1.5mv,解得v=,由能量守恒定律有m+×0.5m=Q+2Q+×1.5m,解得Q=m,选项B错误,D正确.
【针对性训练】
1.(18分)(2024年5月四川重点高中质检)如图甲所示,水平面上固定着间距为的两条平行直轨道(除是绝缘的连接段外,其他轨道均为不计电阻的导体),之间有一个的定值电阻,的左侧轨道内分布着竖直向下的匀强磁场,该磁场随时间的变化情况如图乙所示,的右侧轨道内分布着垂直导轨平面的匀强磁场,磁感应强度,方向竖直向上、时刻,质量、电阻的a棒静止在距离导轨左侧处,质量、电阻的b棒在距离右侧处被一种特定的装置锁定,两棒均长,且与轨道接触良好。左侧的轨道与棒间的动摩擦因数,右侧的轨道光滑且足够长,可认为最大静摩擦力等于滑动摩擦力,不考虑轨道连接处的阻碍。时,对a棒施加水平向右的恒力,在离开磁场区域时已达到稳定的速度,过后撤去恒力。当a棒接触到b棒时,如棒的锁定装置迅速解除,随后两棒碰撞并粘在一起成为一个整体。
(1)时,通过a棒的电流大小及方向(图中向上或向下);
(2)a棒刚进入磁场时,求a棒两端的电势差﹔
(3)求b棒在整个过程中产生的焦耳热;
(4)a棒、b棒在磁场中最终的稳定速度。
【答案】(1)2A,向上;(2)2V;(3)4.5J;(4)1m/s
【解析】(1)内,磁场增强,由楞次定律判断,a棒上的电流方向为向上(逆时针)
假设a棒不动
因为最大静摩擦力为
假设成立,a棒不动。
(2)a棒离开时已达到稳定速度,此时有
可得
a棒以的速度冲入的匀强磁场,
a棒两端的电势差为
(3)考虑a棒进入磁场时,与b棒相距﹐a棒在与b棒相撞前,b棒一定处于静止状态,设a棒与b棒碰撞前瞬间的速度为。
以a棒为研究对象,由动量定理,有
可得a棒在与b棒相撞前的速度为
由能量守恒定律,从a棒刚进入磁场开始到a、b两棒碰撞前瞬间,a棒减少的动能,转化为电能,通过电流做功,释放焦耳热,则
解得
(4)a、b两棒碰撞时,系统动量守恒,最终两棒速度相等
解得
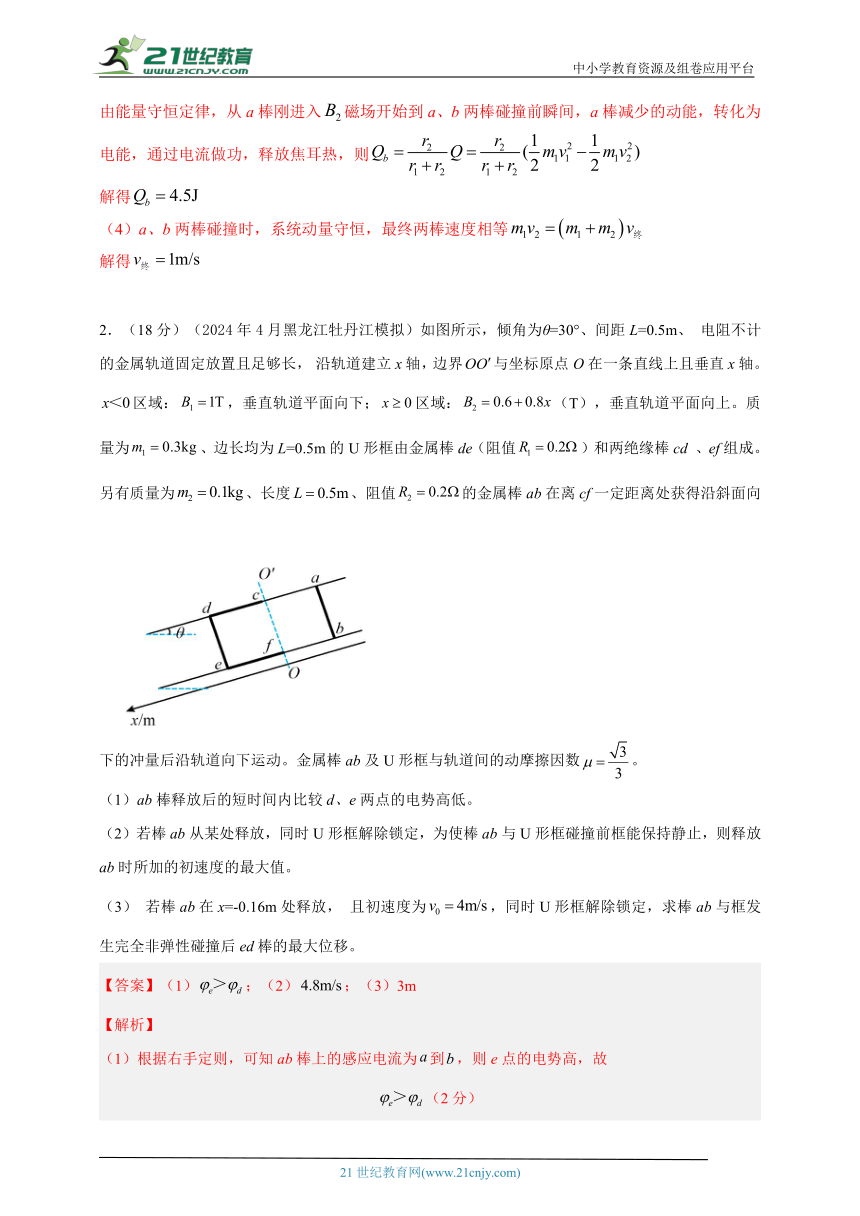
2.(18分)(2024年4月黑龙江牡丹江模拟)如图所示,倾角为θ=30°、间距L=0.5m、 电阻不计的金属轨道固定放置且足够长, 沿轨道建立x轴,边界与坐标原点O在一条直线上且垂直x轴。区域:,垂直轨道平面向下;区域:(T),垂直轨道平面向上。质量为、边长均为L=0.5m的U形框由金属棒de(阻值)和两绝缘棒cd 、ef组成。另有质量为、长度、阻值的金属棒ab在离cf一定距离处获得沿斜面向下的冲量后沿轨道向下运动。金属棒ab及U形框与轨道间的动摩擦因数。
(1)ab棒释放后的短时间内比较d、e两点的电势高低。
(2)若棒ab从某处释放,同时U形框解除锁定,为使棒ab与U形框碰撞前框能保持静止,则释放ab时所加的初速度的最大值。
(3) 若棒ab在x=-0.16m处释放, 且初速度为,同时U形框解除锁定,求棒ab与框发生完全非弹性碰撞后ed棒的最大位移。
【答案】(1);(2);(3)3m
【解析】
(1)根据右手定则,可知ab棒上的感应电流为到,则e点的电势高,故
(2分)
(2)金属棒ab向下运动时,由于
(1分)
重力沿斜面的分力与摩擦力等大反向,因此金属棒ab释放后,在安培力作用下运动,金属棒ab做加速度减小的减速运动,ab受到的安培力为
(1分)
由左手定则可知﹐U形框受到安培力的方向沿导轨平面向上,大小为
(1分)
其中
因此获得冲量的瞬间,U形框受到的安培力最大,最容易发生滑动。为使U形框静止,此时U形框受到的摩擦力沿导轨平面向下为最大静摩擦力,大小为
U形框静止有
(1分)
金属棒ab释放时所加的初速度满足的条件为
(1分)
即释放ab时所加的初速度的最大值。
(3)金属棒ab初速度为,则金属棒ab在安培力作用下做加速度减小的减速运动,而U形框在碰撞前始终处于静止。设到达时速度为,以沿导轨平面向下为正方向,由动量定理得
(2分)
其中
(1分)
解得
(1分)
金属棒ab与U形框发生完全非弹性碰撞,由动量守恒得
(1分)
因此碰撞后U形框速度为
(1分)
同理,其重力沿导轨平面向下的分力与滑动摩擦力等大反向,合力等于安培力,当U形框速度为v时,其感应电流为
(1分)
其中、分别为de边和ab边处的磁感应强度,电流方向为顺时针方向,受到总的安培力为
(1分)
其中
由动量定理得
(2分)
金属棒ab与框发生完全非弹性碰撞后ed棒的最大位移
(1分)
3.(18分)(2024年4月安徽马鞍山二模)如图所示,有一足够长的水平传送带以的速度始终向左匀速运动,在传送带上的矩形区域内充满匀强磁场,该磁场区域始终随传送带一起以的速度匀速向左运动。某时刻,将两个表面绝缘的正方形导体框a、b同时轻放在传送带上的不同位置,a的右边恰好与重合,b在a的左侧,两导体框中轴线重合且与传送带运动方向平行,两导体框质量均为m,边长均为L,电阻均为R,a与传送带间的动摩擦因数为,b与传送带间无摩擦。一段时间后,导体框a的左边与重合时,a与传送带恰好共速,同时两导体框发生弹性碰撞,碰后两导体框分离,再过一段时间两导体框共速。已知磁场的磁感应强度大小为B、方向竖直向下,,重力加速度为g。求:
(1)导体框a刚进入磁场时的加速度大小;
(2)两导体框共速后,它们之间的距离;
(3)两导体框初始距离d。
【解析】.(18分)
(1)对导体框a:,,
联立解得:
(2)a、b弹性碰撞:,
联立解得:、
由题意可知:两框碰后,导体框a从静止到再次与传送带共速过程,传送带相对a的位移为L,碰撞后导体框b始终与传送带共速。
故两导体框均与传送带共速后,它们之间的距离为L。
(3)导体框a加速过程:
由题意:,
联立解得:
4.(2024江苏六校下学期第二次联考)如图所示,倾角为θ=30°、间距L=0.5m、 电阻不计的金属轨道固定放置且足够长, 沿轨道建立x轴,边界与坐标原点O在一条直线上且垂直x轴。区域:,垂直轨道平面向下;区域:(T),垂直轨道平面向上。质量为、边长均为L=0.5m的U形框由金属棒de(阻值)和两绝缘棒cd 、ef组成。另有质量为、长度、阻值的金属棒ab在离cf一定距离处获得沿斜面向下的冲量后沿轨道向下运动。金属棒ab及U形框与轨道间的动摩擦因数。
(1)ab棒释放后的短时间内比较d、e两点的电势高低。
(2)若棒ab从某处释放,同时U形框解除锁定,为使棒ab与U形框碰撞前框能保持静止,则释放ab时所加的初速度的最大值。
(3) 若棒ab在x=-0.16m处释放, 且初速度为,同时形框解除锁定,求棒ab与框发生完全非弹性碰撞后ed棒的最大位移。
【答案】(1);(2);(3)3m
【解析】
(1)根据右手定则,可知ab棒上的感应电流为到,则e点的电势高,故
(2)金属棒ab向下运动时,由于
重力沿斜面的分力与摩擦力等大反向,因此金属棒ab释放后,在安培力作用下运动,金属棒ab做加速度减小的减速运动,ab受到的安培力为
由左手定则可知﹐U形框受到安培力的方向沿导轨平面向上,大小为
其中
因此获得冲量的瞬间,U形框受到的安培力最大,最容易发生滑动。为使U形框静止,此时U形框受到的摩擦力沿导轨平面向下为最大静摩擦力,大小为
U形框静止有
金属棒ab释放时所加的初速度满足的条件为
即释放ab时所加的初速度的最大值。
(3)金属棒ab初速度为,则金属棒ab在安培力作用下做加速度减小的减速运动,而U形框在碰撞前始终处于静止。设到达时速度为,以沿导轨平面向下为正方向,由动量定理得
其中
解得
金属棒ab与U形框发生完全非弹性碰撞,由动量守恒得
因此碰撞后U形框速度为
同理,其重力沿导轨平面向下的分力与滑动摩擦力等大反向,合力等于安培力,当U形框速度为v时,其感应电流为
其中、分别为de边和ab边处的磁感应强度,电流方向为顺时针方向,受到总的安培力为
其中
由动量定理得
金属棒ab与框发生完全非弹性碰撞后ed棒的最大位移
5. (2024河南新郑实验高中3月质检)(12分)如图所示,MCN与PDQ是一组足够长的平行光滑导轨,间距,MC、PD倾斜,CN、DQ在同一水平面内,CD与CN垂直,C、D处平滑连接。水平金属导轨间有竖直向下的匀强磁场,磁感应强度。质量、电阻、长度为L的硬质导体棒a静止在水平轨道上,与a完全相同的导体棒b从距水平面高度的倾斜绝缘轨道上由静止释放,最后恰好不与a棒相撞,运动过程中a、b棒始终与导轨垂直且接触良好。不计其他电阻和空气阻力,重力加速度g取。
(1)求b棒刚进入磁场时,a棒所受安培力的大小;
(2)求整个过程中通过a棒的电荷量q及a棒距离CD的初始距离;
(3)a、b棒稳定后,在释放b棒的初始位置由静止释放相同的棒,所有棒运动稳定后,在同一位置再由静止释放相同的棒,所有棒运动再次稳定后,依此类推,逐一由静止释放、、……、。当释放的最终与所有棒运动稳定后,求从棒开始释放到与所有棒运动保持相对稳定时,回路中产生的焦耳热。
【答案】(1)1N;(2)0.1C,0.2m;(3)
【解析】(1)根据题意,对棒由动能定理可得,
棒刚进入磁场时,感应电动势,
回路中的电流,
安培力,
联立可得
(2)对棒由动量守恒定律可得,
对棒由动量定理可得,
电荷量,
解得,
由(1)问可得,可得
(3)当棒运动达到稳定后有,
当棒运动达到稳定后有,
当棒运动达到稳定后有,
可得,则,
回路中产生的焦耳热,
解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
高中物理选择性必修二素养提升学案
第二章 电磁感应
专题强化2.7 动量守恒定律在电磁感应中的应用
【专题解读】
在两等长金属棒切割磁感线的系统中,两金属棒和水平平行金属导轨构成闭合回路,它们受到的安培力的合力为0,如果不计摩擦,它们受到的合力为0,满足动量守恒的条件,运用动量守恒定律解题比较方便.
方法点拨
双棒无外力 双棒有外力
示意图 F为恒力
动力学观点 导体棒1受安培力的作用做加速度逐渐减小的减速运动,导体棒2受安培力的作用做加速度逐渐减小的加速运动,最终两棒以相同的速度做匀速直线运动 导体棒1做加速度逐渐减小的加速运动,导体棒2做加速度逐渐增大的加速运动,最终两棒以相同的加速度做匀加速直线运动
动量观点 系统动量守恒 系统动量不守恒
能量观点 棒1动能的减少量=棒2动能的增加量+焦耳热 力F做的功=棒1的动能+棒2的动能+焦耳热
【典例剖析】
【典例】(2021福建卷)如图,P、Q是两根固定在水平面内的光滑平行金属导轨,间距为L,导轨足够长且电阻可忽略不计.图中EFHG矩形区域内有方向垂直导轨平面向上、磁感应强度大小为B的匀强磁场.在t=t1时刻,两均匀金属棒a、b分别从磁场边界EF、GH进入磁场,速度大小均为v0;一段时间后,流经a棒的电流为0,此时t=t2,b棒仍位于磁场区域内.已知金属棒a、b由相同材料制成,长度均为L,电阻分别为R和2R,a棒的质量为m.在运动过程中两金属棒始终与导轨垂直且接触良好,a、b棒没有相碰,则( AD )
A.t1时刻a棒的加速度大小为
B.t2时刻b棒的速度为0
C.t1~t2时间内,通过a棒横截面的电荷量是b棒的2倍
D.t1~t2时间内,a棒产生的焦耳热为m
解析 在t=t1时刻,两均匀金属棒a、b分别从磁场边界EF、GH进入磁场,速度大小均为v0,由右手定则可判断出两金属棒产生的感应电流方向都是逆时针方向,产生的感应电动势都是BLv0,由闭合电路欧姆定律可得,t1时刻a金属棒中的感应电流I==,受到的安培力F=BIL=,由牛顿第二定律F=ma可得,t1时刻a棒的加速度大小为a=,选项A正确;由于金属棒a、b串联构成回路,所以在t1~t2时间内,通过a棒横截面的电荷量与b棒的相同,选项C错误;由于金属棒a、b电阻分别为R和2R,金属棒a、b串联构成回路,二者电流相等,由焦耳定律可知金属棒a、b产生的焦耳热之比为1∶2,设t1~t2时间内,a棒产生的焦耳热为Q,则b棒产生的焦耳热为2Q,又两者材料相同,由电阻定律可知,金属棒a的横截面积为b的2倍,故体积为b的2倍,质量为b的2倍,即b的质量为0.5m,t=t2时刻流经a棒的电流为0,且b棒仍位于磁场区域内,说明金属棒a、b具有共同速度,由动量守恒定律有mv0-0.5mv0=1.5mv,解得v=,由能量守恒定律有m+×0.5m=Q+2Q+×1.5m,解得Q=m,选项B错误,D正确.
【针对性训练】
1.(18分)(2024年5月四川重点高中质检)如图甲所示,水平面上固定着间距为的两条平行直轨道(除是绝缘的连接段外,其他轨道均为不计电阻的导体),之间有一个的定值电阻,的左侧轨道内分布着竖直向下的匀强磁场,该磁场随时间的变化情况如图乙所示,的右侧轨道内分布着垂直导轨平面的匀强磁场,磁感应强度,方向竖直向上、时刻,质量、电阻的a棒静止在距离导轨左侧处,质量、电阻的b棒在距离右侧处被一种特定的装置锁定,两棒均长,且与轨道接触良好。左侧的轨道与棒间的动摩擦因数,右侧的轨道光滑且足够长,可认为最大静摩擦力等于滑动摩擦力,不考虑轨道连接处的阻碍。时,对a棒施加水平向右的恒力,在离开磁场区域时已达到稳定的速度,过后撤去恒力。当a棒接触到b棒时,如棒的锁定装置迅速解除,随后两棒碰撞并粘在一起成为一个整体。
(1)时,通过a棒的电流大小及方向(图中向上或向下);
(2)a棒刚进入磁场时,求a棒两端的电势差﹔
(3)求b棒在整个过程中产生的焦耳热;
(4)a棒、b棒在磁场中最终的稳定速度。
【答案】(1)2A,向上;(2)2V;(3)4.5J;(4)1m/s
【解析】(1)内,磁场增强,由楞次定律判断,a棒上的电流方向为向上(逆时针)
假设a棒不动
因为最大静摩擦力为
假设成立,a棒不动。
(2)a棒离开时已达到稳定速度,此时有
可得
a棒以的速度冲入的匀强磁场,
a棒两端的电势差为
(3)考虑a棒进入磁场时,与b棒相距﹐a棒在与b棒相撞前,b棒一定处于静止状态,设a棒与b棒碰撞前瞬间的速度为。
以a棒为研究对象,由动量定理,有
可得a棒在与b棒相撞前的速度为
由能量守恒定律,从a棒刚进入磁场开始到a、b两棒碰撞前瞬间,a棒减少的动能,转化为电能,通过电流做功,释放焦耳热,则
解得
(4)a、b两棒碰撞时,系统动量守恒,最终两棒速度相等
解得
2.(18分)(2024年4月黑龙江牡丹江模拟)如图所示,倾角为θ=30°、间距L=0.5m、 电阻不计的金属轨道固定放置且足够长, 沿轨道建立x轴,边界与坐标原点O在一条直线上且垂直x轴。区域:,垂直轨道平面向下;区域:(T),垂直轨道平面向上。质量为、边长均为L=0.5m的U形框由金属棒de(阻值)和两绝缘棒cd 、ef组成。另有质量为、长度、阻值的金属棒ab在离cf一定距离处获得沿斜面向下的冲量后沿轨道向下运动。金属棒ab及U形框与轨道间的动摩擦因数。
(1)ab棒释放后的短时间内比较d、e两点的电势高低。
(2)若棒ab从某处释放,同时U形框解除锁定,为使棒ab与U形框碰撞前框能保持静止,则释放ab时所加的初速度的最大值。
(3) 若棒ab在x=-0.16m处释放, 且初速度为,同时U形框解除锁定,求棒ab与框发生完全非弹性碰撞后ed棒的最大位移。
【答案】(1);(2);(3)3m
【解析】
(1)根据右手定则,可知ab棒上的感应电流为到,则e点的电势高,故
(2分)
(2)金属棒ab向下运动时,由于
(1分)
重力沿斜面的分力与摩擦力等大反向,因此金属棒ab释放后,在安培力作用下运动,金属棒ab做加速度减小的减速运动,ab受到的安培力为
(1分)
由左手定则可知﹐U形框受到安培力的方向沿导轨平面向上,大小为
(1分)
其中
因此获得冲量的瞬间,U形框受到的安培力最大,最容易发生滑动。为使U形框静止,此时U形框受到的摩擦力沿导轨平面向下为最大静摩擦力,大小为
U形框静止有
(1分)
金属棒ab释放时所加的初速度满足的条件为
(1分)
即释放ab时所加的初速度的最大值。
(3)金属棒ab初速度为,则金属棒ab在安培力作用下做加速度减小的减速运动,而U形框在碰撞前始终处于静止。设到达时速度为,以沿导轨平面向下为正方向,由动量定理得
(2分)
其中
(1分)
解得
(1分)
金属棒ab与U形框发生完全非弹性碰撞,由动量守恒得
(1分)
因此碰撞后U形框速度为
(1分)
同理,其重力沿导轨平面向下的分力与滑动摩擦力等大反向,合力等于安培力,当U形框速度为v时,其感应电流为
(1分)
其中、分别为de边和ab边处的磁感应强度,电流方向为顺时针方向,受到总的安培力为
(1分)
其中
由动量定理得
(2分)
金属棒ab与框发生完全非弹性碰撞后ed棒的最大位移
(1分)
3.(18分)(2024年4月安徽马鞍山二模)如图所示,有一足够长的水平传送带以的速度始终向左匀速运动,在传送带上的矩形区域内充满匀强磁场,该磁场区域始终随传送带一起以的速度匀速向左运动。某时刻,将两个表面绝缘的正方形导体框a、b同时轻放在传送带上的不同位置,a的右边恰好与重合,b在a的左侧,两导体框中轴线重合且与传送带运动方向平行,两导体框质量均为m,边长均为L,电阻均为R,a与传送带间的动摩擦因数为,b与传送带间无摩擦。一段时间后,导体框a的左边与重合时,a与传送带恰好共速,同时两导体框发生弹性碰撞,碰后两导体框分离,再过一段时间两导体框共速。已知磁场的磁感应强度大小为B、方向竖直向下,,重力加速度为g。求:
(1)导体框a刚进入磁场时的加速度大小;
(2)两导体框共速后,它们之间的距离;
(3)两导体框初始距离d。
【解析】.(18分)
(1)对导体框a:,,
联立解得:
(2)a、b弹性碰撞:,
联立解得:、
由题意可知:两框碰后,导体框a从静止到再次与传送带共速过程,传送带相对a的位移为L,碰撞后导体框b始终与传送带共速。
故两导体框均与传送带共速后,它们之间的距离为L。
(3)导体框a加速过程:
由题意:,
联立解得:
4.(2024江苏六校下学期第二次联考)如图所示,倾角为θ=30°、间距L=0.5m、 电阻不计的金属轨道固定放置且足够长, 沿轨道建立x轴,边界与坐标原点O在一条直线上且垂直x轴。区域:,垂直轨道平面向下;区域:(T),垂直轨道平面向上。质量为、边长均为L=0.5m的U形框由金属棒de(阻值)和两绝缘棒cd 、ef组成。另有质量为、长度、阻值的金属棒ab在离cf一定距离处获得沿斜面向下的冲量后沿轨道向下运动。金属棒ab及U形框与轨道间的动摩擦因数。
(1)ab棒释放后的短时间内比较d、e两点的电势高低。
(2)若棒ab从某处释放,同时U形框解除锁定,为使棒ab与U形框碰撞前框能保持静止,则释放ab时所加的初速度的最大值。
(3) 若棒ab在x=-0.16m处释放, 且初速度为,同时形框解除锁定,求棒ab与框发生完全非弹性碰撞后ed棒的最大位移。
【答案】(1);(2);(3)3m
【解析】
(1)根据右手定则,可知ab棒上的感应电流为到,则e点的电势高,故
(2)金属棒ab向下运动时,由于
重力沿斜面的分力与摩擦力等大反向,因此金属棒ab释放后,在安培力作用下运动,金属棒ab做加速度减小的减速运动,ab受到的安培力为
由左手定则可知﹐U形框受到安培力的方向沿导轨平面向上,大小为
其中
因此获得冲量的瞬间,U形框受到的安培力最大,最容易发生滑动。为使U形框静止,此时U形框受到的摩擦力沿导轨平面向下为最大静摩擦力,大小为
U形框静止有
金属棒ab释放时所加的初速度满足的条件为
即释放ab时所加的初速度的最大值。
(3)金属棒ab初速度为,则金属棒ab在安培力作用下做加速度减小的减速运动,而U形框在碰撞前始终处于静止。设到达时速度为,以沿导轨平面向下为正方向,由动量定理得
其中
解得
金属棒ab与U形框发生完全非弹性碰撞,由动量守恒得
因此碰撞后U形框速度为
同理,其重力沿导轨平面向下的分力与滑动摩擦力等大反向,合力等于安培力,当U形框速度为v时,其感应电流为
其中、分别为de边和ab边处的磁感应强度,电流方向为顺时针方向,受到总的安培力为
其中
由动量定理得
金属棒ab与框发生完全非弹性碰撞后ed棒的最大位移
5. (2024河南新郑实验高中3月质检)(12分)如图所示,MCN与PDQ是一组足够长的平行光滑导轨,间距,MC、PD倾斜,CN、DQ在同一水平面内,CD与CN垂直,C、D处平滑连接。水平金属导轨间有竖直向下的匀强磁场,磁感应强度。质量、电阻、长度为L的硬质导体棒a静止在水平轨道上,与a完全相同的导体棒b从距水平面高度的倾斜绝缘轨道上由静止释放,最后恰好不与a棒相撞,运动过程中a、b棒始终与导轨垂直且接触良好。不计其他电阻和空气阻力,重力加速度g取。
(1)求b棒刚进入磁场时,a棒所受安培力的大小;
(2)求整个过程中通过a棒的电荷量q及a棒距离CD的初始距离;
(3)a、b棒稳定后,在释放b棒的初始位置由静止释放相同的棒,所有棒运动稳定后,在同一位置再由静止释放相同的棒,所有棒运动再次稳定后,依此类推,逐一由静止释放、、……、。当释放的最终与所有棒运动稳定后,求从棒开始释放到与所有棒运动保持相对稳定时,回路中产生的焦耳热。
【答案】(1)1N;(2)0.1C,0.2m;(3)
【解析】(1)根据题意,对棒由动能定理可得,
棒刚进入磁场时,感应电动势,
回路中的电流,
安培力,
联立可得
(2)对棒由动量守恒定律可得,
对棒由动量定理可得,
电荷量,
解得,
由(1)问可得,可得
(3)当棒运动达到稳定后有,
当棒运动达到稳定后有,
当棒运动达到稳定后有,
可得,则,
回路中产生的焦耳热,
解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
