期末提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 期末提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 21:04:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末提优测评卷
时间:120分钟 总分:120分
第Ⅰ卷(选择题 共24分)
一、选择题(每题3分,共24分)
1.(2024·盐城中考)矩形相邻两边长分别为 cm、 cm,设其面积为Scm ,则 S 在哪两个连续整数之间( ).
A. 1和2 B. 2和3 C. 3和4 D. 4和5
2.(2024·扬州宝应期末)在一个不透明的袋中装有2个红球和若干个白球(除颜色外其余均相同),摇匀后从中随机摸出一个球,经过大量重复的试验后发现摸出红球的频率稳定在25%,则袋中白球的数量是( ).
A. 2 B. 4 C. 6 D. 8
3.下列调查适合采用抽样调查的是( ).
A. 了解一批灯泡的使用寿命 B.了解全班同学的身高
C.检查航天飞行器的零部件 D.对入境人员进行检测
4.(2024·巴中中考)某班学生乘汽车从学校出发去参加活动,目的地距学校60km,一部分学生乘慢车先行0.5h,另一部分学生再乘快车前往,他们同时到达.已知快车的速度比慢车的速度每小时快20km,求慢车的速度 设慢车的速度为 xkm/h,则可列方程为( ).
5.关于反比例函数 的下列说法不正确的是( ).
①该函数的图像在第二、四象限;
②A(x ,y )、B(x ,y )两点在该函数图像上,若x③当x>2时,y>-2.
A. ①②③ B. ①③ C. ②③ D. 以上均不正确
6.如图,将菱形竖直位置的对角线向右平移a cm,水平位置的对角线向上平移b cm,平移后菱形被分成四块,最大一块与最小一块的面积和记为S ,其余两块的面积和记为S ,则S 与S 的差是( ).
A. ab cm B. 2ab cm D. 4ab cm
7. 如图,四边形ABCD是平行四边形,过点A作AM⊥BC于点M,交BD于点E,过点C作CN⊥AD于点N,交BD于点F,连接CE、AF,当EA=EC,且点M 为BC的中点时,AB:AE的值为( ).
A. 2 B. C. D.
8.如图,点 P 为定角∠AOB 的平分线上的一个定点,且∠MPN与∠AOB 互补.若∠MPN 在绕点P 旋转的过程中,其两边分别与OA、OB 相交于M、N 两点,则以下结论:①PM=PN;②OM+ON 的值不变;③MN 的长不变;④四边形 PMON 的面积不变.其中,结论正确的是( ).
A. ①②③ B. ①②④ C. ①③④ D. ②③④
第Ⅱ卷(非选择题 共96分)
二、填空题(每题3分,共30分)
9.(2023·凉山州中考)计算(
10.如图是函数y=x和函数 在第一象限部分的图像,则x>0时,使 成立的x的取值范围是 .
11.若分式 的值为0,则x的值为 .
12. (2024·牡丹江中考)函数 中,自变量x的取值范围是 .
13. 已知 是反比例函数,则m的值为 .
14.(2024·常州溧阳期末)反比例函数 的图像经过(a,3)、(a+2,6)、(b,-12)三点,则b的值为 .
15.(2024·牡丹江中考)若分式方程 的解为正整数,则整数m的值为 .
16.实数a、b在数轴上的位置如图所示,则化简、 的结果是 .
17.如图,正方形ABCD 的边长为1,点 M 是边CD 的中点,将△BCM 沿直线BM 翻折,使得点C落在同一平面内的点E 处,连接AE 并延长交射线BM 于点F,那么 EF 的长为 .
18.已知一次函数 与反比例函数 中,函数y 、y 与自变量x的部分对应值分别如表1、表2所示:
x -1 1 2
y -4 4 2 .
表1: 表2:
x -4 0 1
y -1 3 4
则关于x的不等式 的解集是 .
三、解答题(第19~22题每题7分,第23、24题每题9分,第25、26题每题10分,共66分)
19. 计算:
20. (1)(2024·巴中中考)先化简,再求值 其中
(2)(2024·福建中考)解方程
21. 如图,在△ABC中,D 是边BC上一点,AD=AB.
(1)请用尺规作图法作△ABC 绕点A 旋转后得到的△ADE,使旋转后的边AB 与边AD 重合;(保留作图痕迹,不写作法)
(2)连接CE,若∠B=60°,求证:CE=AE.
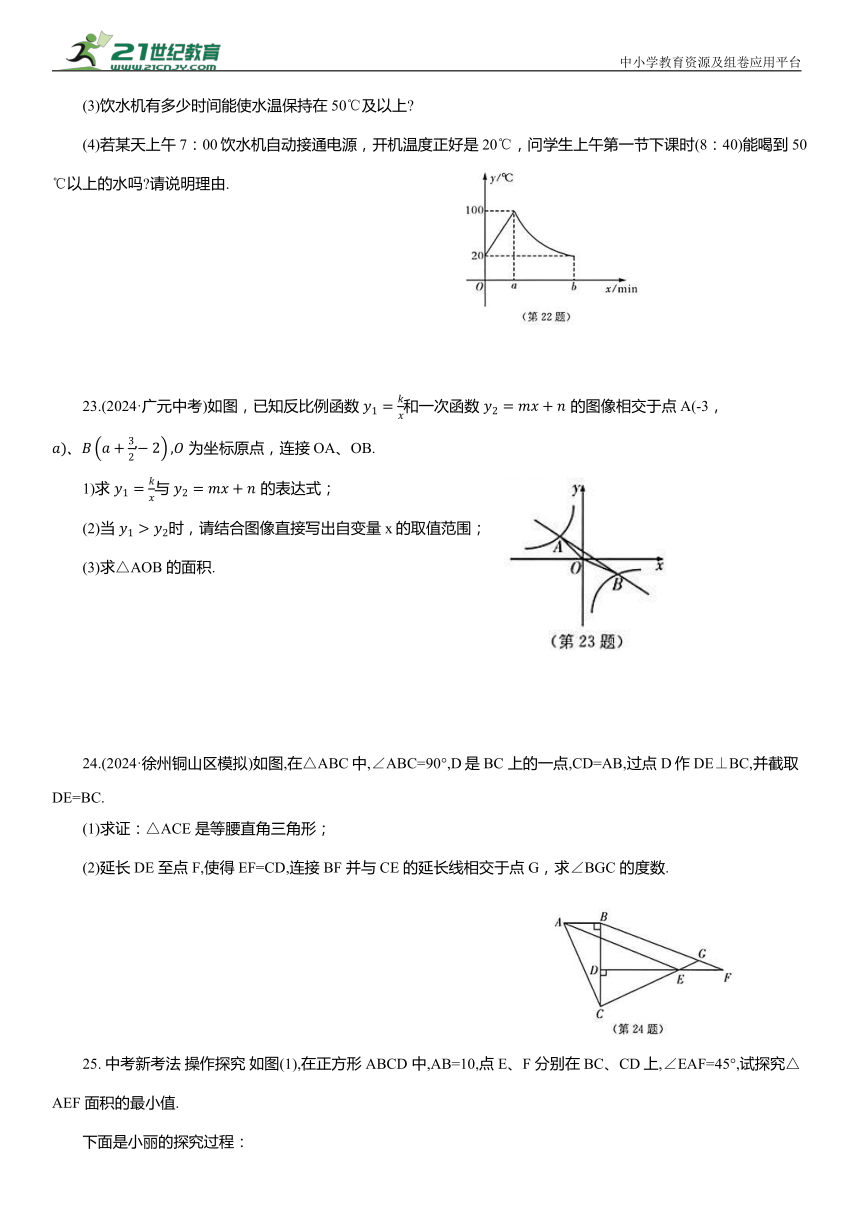
22.我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至 20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示.
(2)直接写出图中y关于x的函数表达式.
(3)饮水机有多少时间能使水温保持在50℃及以上
(4)若某天上午7:00饮水机自动接通电源,开机温度正好是20℃,问学生上午第一节下课时(8:40)能喝到50℃以上的水吗 请说明理由.
23.(2024·广元中考)如图,已知反比例函数 和一次函数 的图像相交于点A(-3, 为坐标原点,连接OA、OB.
1)求 与 的表达式;
(2)当 时,请结合图像直接写出自变量x的取值范围;
(3)求△AOB 的面积.
24.(2024·徐州铜山区模拟)如图,在△ABC中,∠ABC=90°,D是BC 上的一点,CD=AB,过点 D作DE⊥BC,并截取DE=BC.
(1)求证:△ACE 是等腰直角三角形;
(2)延长DE 至点F,使得EF=CD,连接BF 并与CE 的延长线相交于点G,求∠BGC 的度数.
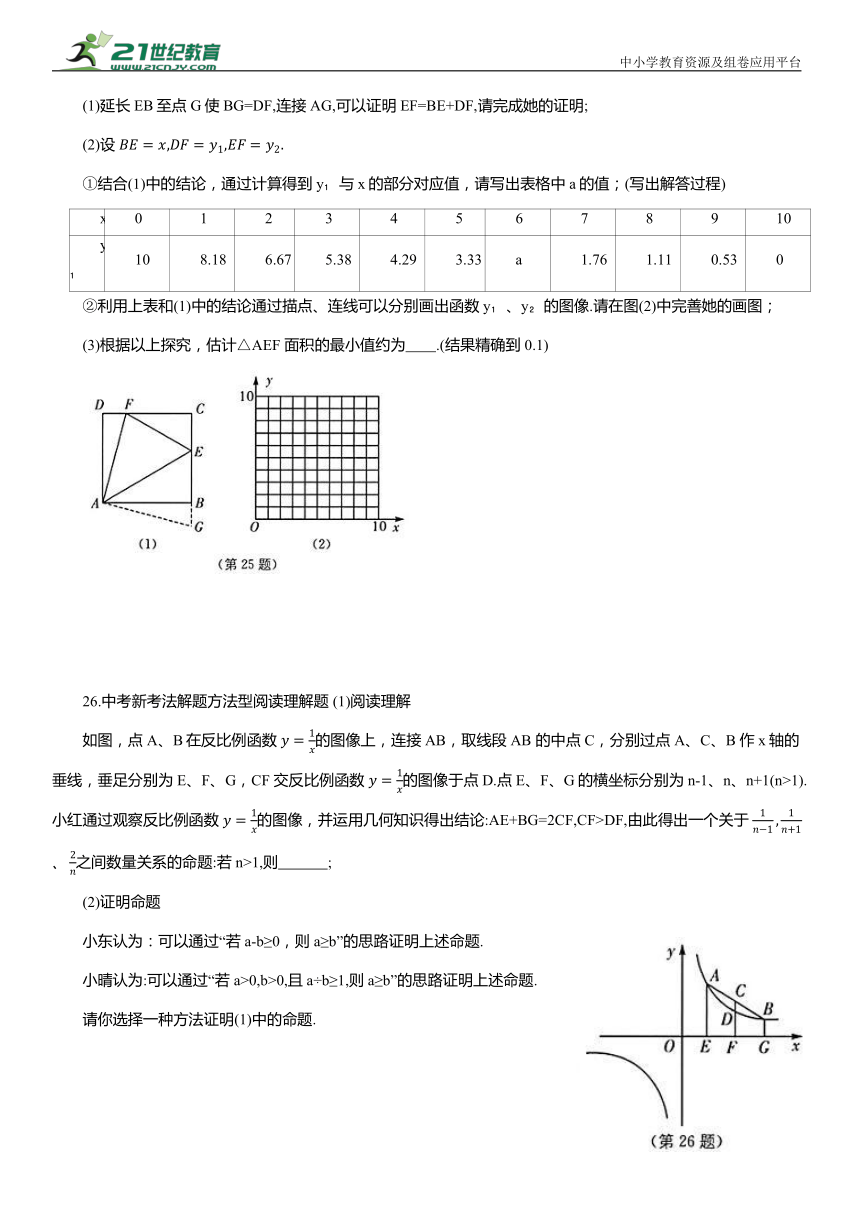
25. 中考新考法 操作探究 如图(1),在正方形ABCD 中,AB=10,点 E、F 分别在BC、CD上,∠EAF=45°,试探究△AEF 面积的最小值.
下面是小丽的探究过程:
(1)延长EB至点G使BG=DF,连接AG,可以证明EF=BE+DF,请完成她的证明;
(2)设
①结合(1)中的结论,通过计算得到y 与x的部分对应值,请写出表格中a的值;(写出解答过程)
x 0 1 2 3 4 5 6 7 8 9 10
y 10 8.18 6.67 5.38 4.29 3.33 a 1.76 1.11 0.53 0
②利用上表和(1)中的结论通过描点、连线可以分别画出函数y 、y 的图像.请在图(2)中完善她的画图;
(3)根据以上探究,估计△AEF 面积的最小值约为 .(结果精确到0.1)
26.中考新考法解题方法型阅读理解题 (1)阅读理解
如图,点A、B在反比例函数 的图像上,连接AB,取线段AB 的中点C,分别过点A、C、B 作x轴的垂线,垂足分别为E、F、G,CF 交反比例函数 的图像于点D.点E、F、G的横坐标分别为n-1、n、n+1(n>1).小红通过观察反比例函数 的图像,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于 之间数量关系的命题:若n>1,则 ;
(2)证明命题
小东认为:可以通过“若a-b≥0,则a≥b”的思路证明上述命题.
小晴认为:可以通过“若a>0,b>0,且a÷b≥1,则a≥b”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
1. C [解析]S= = ,9<10<16,∴ 即 S 在3 和4之间.故选C.
2. C [解析]根据题意知,袋中球的总个数约为2÷0.25=8(个),所以袋中白球的个数约为8--2=6(个).故选 C.
3. A
4. A [解析]设慢车的速度为x km/h,则快车的速度为(x+20) km/h,根据题意可得 故选 A.
5. C [解析]∵ 反比例函数的图像在二、四象限,故①正确;
A(x ,y )、B(x ,y )两点在该函数图像上,且. ∵无法判断A、B 的具体位置,∴不能确定 y 与y 的大小,故②错误;
∵x=2时,y=-2,∴当x>2时,-26. D [解析]如图,作 HK 关于AC 的对称线段GL,作FE 关于 BD 的对称线段 IJ,由对称性可知,图中对应颜色的部分面积相等,∴S 与S 的差=4S四边形OMPN·
∵OM=a cm,ON=b cm,∴4S四边形OMPN=4ab cm .故选 D.
7. B [解析]如图,连接AC.
∵四边形ABCD 是平行四边形,∴BC∥AD,BC=AD,∴∠ADE=∠CBD.
在△ADE 和△CBF 中.
∴△ADE≌△CBF(ASA),∴AE=CF.
又AM⊥BC,∴AM⊥AD.
∵CN⊥AD,∴AM∥CN,∴AE∥CF,
∴四边形AECF 为平行四边形.
∵EA=EC,∴四边形AECF 是菱形,∴AC⊥BD.
∴四边形ABCD 是菱形,∴AB=BC.
∵M是 BC 的中点,AM⊥BC,∴AB=AC,∴△ABC为等边三角形,∴∠ABC=60°,∠CBD=30°.
∴在 Rt△BCF中,1 又AE=CF,
AB=BC,∴AB:AE= 故选 B.
8. B [解析]如图,过点 P 作PE⊥OA 于点E,PF⊥OB于点F,∴∠PEO=∠PFO=90°,∴∠EPF+∠AOB=180°.∵∠MPN+∠AOB=180°,
∴∠EPF = ∠MPN, ∴ ∠EPF - ∠EPN =∠MPN-∠EPN,∴∠EPM=∠FPN.
∵OP 平分∠AOB,∴∠POE=∠POF.
在△POE 和△POF 中.
∴△POE≌△POF(AAS),∴OE=OF,PE=PF.
在△PEM 和△PFN 中.
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,故①正确;
∵△PEM≌△PFN,∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故④正确;
∵OM+ON=OE+ME+(OF--NF)=2OE,是定值,故②正确;
在旋转过程中,△PMN 是顶角不变的等腰三角形,因为 PM的长度是变化的,所以 MN 的长度也是变化的,故③错误.故选 B.
9. [解析]原式:
[解析]令 解得 (负值舍去).根据图像可知,使 在第一象限内成立的x的取值范围是
11.-2 [解析]由题意,得 解得x=-2.
12.x≥-3且x≠0 [解析]根据题意,得 解得x≥-3且x≠0.
13.1 [解析]∵ 是反比例函数, 解得m=1.
14.1 [解析]∵反比例函数 的图像经过(a,3)、(a+2,6),∴3a=(a+2)×6,∴a=-4,
∴反比例函数 的图像经过(-4,3),即k=-4×3=-12,∴反比例函数的表达式为 令y=-12,则
15.—1 [解析]化简,得
去分母,得x=3(x-1)+ mx,
移项、合并同类项,得(2+m)x=3,解得 由方程的解是正整数,得到x为正整数,
即2+m=1或2+m=3,解得m=--1或m=1(舍去,会使得分式无意义).
16.3b [解析]由数轴可知,b>0,a-b<0,a+b<0,∴原式=|b|+|a--b|--|a+b|=b--(a-b)+(a+b)=b--a+b+a+b=3b.
[解析]如图,过点 B 作 BH⊥AF 于点 H,连接EC交BM于点G.
∵正方形ABCD 的边长为1,点 M 是边CD 的中点,
∴BA=BC=CD=1,CM=
∵将△BCM 沿直线BM 翻折,点 C 与点 E 重合,
∴EC⊥BM,BE=BC=CD=1,CM=EM=
∵BH⊥AF,BE=BA=1,∴∠EBH= ∠EBA.
18. x>1或--4解得
即一次函数的表达式为
∵点(1,4)在反比例函数 的图像上,
解得 ,即反比例函数的表达式为
点((--4,-1)也在反比例函数的图像上.
结合题表可知,两图像的交点坐标为(-4,-1)和
(1,4),∴不等式 的解集是x>1或-419.(1)原式
(2)原式
20.(1)原式
当 时,原式
(2)原方程两边都乘(x+2)(x-2),
去分母,得3(x-2)+(x+2)(x-2)=x(x+2),
整理,得3x-10=2x,解得x=10,
检验:当x=10时,(x+2)(x-2)≠0,
故原方程的解为x=10.
21.(1)如图所示,△ADE 即为所求.
(2)如图,连接CE.
∵AB=AD,∠B=60°,
∴△ABD 是等边三角形,∴∠BAD=60°.
∵△ABC 旋转至△ADE,∴△ABC≌△ADE,
∴AC=AE,∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠CAE=∠BAD=60°,
∴△ACE 是等边三角形,∴CE=AE.
22.(1)8 40
(2)由(1)中计算,得
(3)在y=10x+20(0≤x≤8)中,令y=50,解得x=3;
在反比例函数 中,
令y=50,解得x=16.
∴饮水机的水温保持在50℃及以上的时间有16-3=13(分钟).
(4)不能.理由如下:
由题意可知,饮水机工作是以40分钟为一个循环,上午7:00 到上午第一节下课时(8:40)的时间是100分钟,是2个40分钟多20分钟,
∴学生上午第一节下课时(8:40)不能喝到超过50℃的水.
23.(1)∵反比例函数 和一次函数. 的图像相交于点A(-3,a)、B(a+ ,--2),
∴点A(-3,3)、B( ,-2),
把A(--3,3)、B( ,-2)代入 y= mx+n得 解得
(2)由图像可知,当. 时,自变量x的取值范围为-3(3)设AB 与y轴相交于点C,∴C(0,1),
24.(1)∵DE⊥BC,
∴∠EDC=90°=∠CBA,∠DCE+∠DEC=90°.
在△ABC和△CDE 中
∴△ABC≌△CDE(SAS),
∴∠ACB=∠DEC,AC=CE,
∴∠ACB+∠DCE=∠ACE=90°,
∴△ACE 是等腰直角三角形.
(2)∵AB⊥BC,DE⊥BC,∴AB∥DF.
∵AB=CD,EF=CD,∴AB=EF,
∴四边形 AEFB 是平行四边形,
∴BF∥AE,∴∠BGC=∠AEC.
∵△ACE 是等腰直角三角形,
∴∠AEC=45°,∴∠BGC=∠AEC=45°.
25.(1)∵四边形ABCD 是正方形,
∴AD=AB,∠ADF=∠ABG=90°.
又DF=BG,∴△ADF≌△ABG(SAS).
∴∠DAF=∠BAG,AG=AF.
∴ ∠EAG = ∠BAG + ∠BAE = ∠DAF +
又AF=AG,AE=AE,
∴△AFE≌△AGE(SAS).
∴EF=EG=BE+BG=BE+DF.
(2)①当x=6时,CE=BC-BE=10-6=4,设DF=a,则CF=10-a,EF=BE+DF=6+a.在Rt△CEF中,由勾股定理,得 a) ,解得a=2.5.
②由(1),得.
描点画图如下:
(3)41.5 [解析]从图像可以看出y 的最小值约为8.29.∴△AEF 面积的最小值=△AEG 面积的最小值 8.29=41.45≈41.5.
[解析]∵AE+BG=2CF,
(2)选择小东的思路证明如下(答案不唯一):
∵n>1,∴n(n-1)(n+1)>0,
期末提优测评卷
时间:120分钟 总分:120分
第Ⅰ卷(选择题 共24分)
一、选择题(每题3分,共24分)
1.(2024·盐城中考)矩形相邻两边长分别为 cm、 cm,设其面积为Scm ,则 S 在哪两个连续整数之间( ).
A. 1和2 B. 2和3 C. 3和4 D. 4和5
2.(2024·扬州宝应期末)在一个不透明的袋中装有2个红球和若干个白球(除颜色外其余均相同),摇匀后从中随机摸出一个球,经过大量重复的试验后发现摸出红球的频率稳定在25%,则袋中白球的数量是( ).
A. 2 B. 4 C. 6 D. 8
3.下列调查适合采用抽样调查的是( ).
A. 了解一批灯泡的使用寿命 B.了解全班同学的身高
C.检查航天飞行器的零部件 D.对入境人员进行检测
4.(2024·巴中中考)某班学生乘汽车从学校出发去参加活动,目的地距学校60km,一部分学生乘慢车先行0.5h,另一部分学生再乘快车前往,他们同时到达.已知快车的速度比慢车的速度每小时快20km,求慢车的速度 设慢车的速度为 xkm/h,则可列方程为( ).
5.关于反比例函数 的下列说法不正确的是( ).
①该函数的图像在第二、四象限;
②A(x ,y )、B(x ,y )两点在该函数图像上,若x
A. ①②③ B. ①③ C. ②③ D. 以上均不正确
6.如图,将菱形竖直位置的对角线向右平移a cm,水平位置的对角线向上平移b cm,平移后菱形被分成四块,最大一块与最小一块的面积和记为S ,其余两块的面积和记为S ,则S 与S 的差是( ).
A. ab cm B. 2ab cm D. 4ab cm
7. 如图,四边形ABCD是平行四边形,过点A作AM⊥BC于点M,交BD于点E,过点C作CN⊥AD于点N,交BD于点F,连接CE、AF,当EA=EC,且点M 为BC的中点时,AB:AE的值为( ).
A. 2 B. C. D.
8.如图,点 P 为定角∠AOB 的平分线上的一个定点,且∠MPN与∠AOB 互补.若∠MPN 在绕点P 旋转的过程中,其两边分别与OA、OB 相交于M、N 两点,则以下结论:①PM=PN;②OM+ON 的值不变;③MN 的长不变;④四边形 PMON 的面积不变.其中,结论正确的是( ).
A. ①②③ B. ①②④ C. ①③④ D. ②③④
第Ⅱ卷(非选择题 共96分)
二、填空题(每题3分,共30分)
9.(2023·凉山州中考)计算(
10.如图是函数y=x和函数 在第一象限部分的图像,则x>0时,使 成立的x的取值范围是 .
11.若分式 的值为0,则x的值为 .
12. (2024·牡丹江中考)函数 中,自变量x的取值范围是 .
13. 已知 是反比例函数,则m的值为 .
14.(2024·常州溧阳期末)反比例函数 的图像经过(a,3)、(a+2,6)、(b,-12)三点,则b的值为 .
15.(2024·牡丹江中考)若分式方程 的解为正整数,则整数m的值为 .
16.实数a、b在数轴上的位置如图所示,则化简、 的结果是 .
17.如图,正方形ABCD 的边长为1,点 M 是边CD 的中点,将△BCM 沿直线BM 翻折,使得点C落在同一平面内的点E 处,连接AE 并延长交射线BM 于点F,那么 EF 的长为 .
18.已知一次函数 与反比例函数 中,函数y 、y 与自变量x的部分对应值分别如表1、表2所示:
x -1 1 2
y -4 4 2 .
表1: 表2:
x -4 0 1
y -1 3 4
则关于x的不等式 的解集是 .
三、解答题(第19~22题每题7分,第23、24题每题9分,第25、26题每题10分,共66分)
19. 计算:
20. (1)(2024·巴中中考)先化简,再求值 其中
(2)(2024·福建中考)解方程
21. 如图,在△ABC中,D 是边BC上一点,AD=AB.
(1)请用尺规作图法作△ABC 绕点A 旋转后得到的△ADE,使旋转后的边AB 与边AD 重合;(保留作图痕迹,不写作法)
(2)连接CE,若∠B=60°,求证:CE=AE.
22.我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至 20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示.
(2)直接写出图中y关于x的函数表达式.
(3)饮水机有多少时间能使水温保持在50℃及以上
(4)若某天上午7:00饮水机自动接通电源,开机温度正好是20℃,问学生上午第一节下课时(8:40)能喝到50℃以上的水吗 请说明理由.
23.(2024·广元中考)如图,已知反比例函数 和一次函数 的图像相交于点A(-3, 为坐标原点,连接OA、OB.
1)求 与 的表达式;
(2)当 时,请结合图像直接写出自变量x的取值范围;
(3)求△AOB 的面积.
24.(2024·徐州铜山区模拟)如图,在△ABC中,∠ABC=90°,D是BC 上的一点,CD=AB,过点 D作DE⊥BC,并截取DE=BC.
(1)求证:△ACE 是等腰直角三角形;
(2)延长DE 至点F,使得EF=CD,连接BF 并与CE 的延长线相交于点G,求∠BGC 的度数.
25. 中考新考法 操作探究 如图(1),在正方形ABCD 中,AB=10,点 E、F 分别在BC、CD上,∠EAF=45°,试探究△AEF 面积的最小值.
下面是小丽的探究过程:
(1)延长EB至点G使BG=DF,连接AG,可以证明EF=BE+DF,请完成她的证明;
(2)设
①结合(1)中的结论,通过计算得到y 与x的部分对应值,请写出表格中a的值;(写出解答过程)
x 0 1 2 3 4 5 6 7 8 9 10
y 10 8.18 6.67 5.38 4.29 3.33 a 1.76 1.11 0.53 0
②利用上表和(1)中的结论通过描点、连线可以分别画出函数y 、y 的图像.请在图(2)中完善她的画图;
(3)根据以上探究,估计△AEF 面积的最小值约为 .(结果精确到0.1)
26.中考新考法解题方法型阅读理解题 (1)阅读理解
如图,点A、B在反比例函数 的图像上,连接AB,取线段AB 的中点C,分别过点A、C、B 作x轴的垂线,垂足分别为E、F、G,CF 交反比例函数 的图像于点D.点E、F、G的横坐标分别为n-1、n、n+1(n>1).小红通过观察反比例函数 的图像,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于 之间数量关系的命题:若n>1,则 ;
(2)证明命题
小东认为:可以通过“若a-b≥0,则a≥b”的思路证明上述命题.
小晴认为:可以通过“若a>0,b>0,且a÷b≥1,则a≥b”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
1. C [解析]S= = ,9<10<16,∴ 即 S 在3 和4之间.故选C.
2. C [解析]根据题意知,袋中球的总个数约为2÷0.25=8(个),所以袋中白球的个数约为8--2=6(个).故选 C.
3. A
4. A [解析]设慢车的速度为x km/h,则快车的速度为(x+20) km/h,根据题意可得 故选 A.
5. C [解析]∵ 反比例函数的图像在二、四象限,故①正确;
A(x ,y )、B(x ,y )两点在该函数图像上,且. ∵无法判断A、B 的具体位置,∴不能确定 y 与y 的大小,故②错误;
∵x=2时,y=-2,∴当x>2时,-2
∵OM=a cm,ON=b cm,∴4S四边形OMPN=4ab cm .故选 D.
7. B [解析]如图,连接AC.
∵四边形ABCD 是平行四边形,∴BC∥AD,BC=AD,∴∠ADE=∠CBD.
在△ADE 和△CBF 中.
∴△ADE≌△CBF(ASA),∴AE=CF.
又AM⊥BC,∴AM⊥AD.
∵CN⊥AD,∴AM∥CN,∴AE∥CF,
∴四边形AECF 为平行四边形.
∵EA=EC,∴四边形AECF 是菱形,∴AC⊥BD.
∴四边形ABCD 是菱形,∴AB=BC.
∵M是 BC 的中点,AM⊥BC,∴AB=AC,∴△ABC为等边三角形,∴∠ABC=60°,∠CBD=30°.
∴在 Rt△BCF中,1 又AE=CF,
AB=BC,∴AB:AE= 故选 B.
8. B [解析]如图,过点 P 作PE⊥OA 于点E,PF⊥OB于点F,∴∠PEO=∠PFO=90°,∴∠EPF+∠AOB=180°.∵∠MPN+∠AOB=180°,
∴∠EPF = ∠MPN, ∴ ∠EPF - ∠EPN =∠MPN-∠EPN,∴∠EPM=∠FPN.
∵OP 平分∠AOB,∴∠POE=∠POF.
在△POE 和△POF 中.
∴△POE≌△POF(AAS),∴OE=OF,PE=PF.
在△PEM 和△PFN 中.
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,故①正确;
∵△PEM≌△PFN,∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故④正确;
∵OM+ON=OE+ME+(OF--NF)=2OE,是定值,故②正确;
在旋转过程中,△PMN 是顶角不变的等腰三角形,因为 PM的长度是变化的,所以 MN 的长度也是变化的,故③错误.故选 B.
9. [解析]原式:
[解析]令 解得 (负值舍去).根据图像可知,使 在第一象限内成立的x的取值范围是
11.-2 [解析]由题意,得 解得x=-2.
12.x≥-3且x≠0 [解析]根据题意,得 解得x≥-3且x≠0.
13.1 [解析]∵ 是反比例函数, 解得m=1.
14.1 [解析]∵反比例函数 的图像经过(a,3)、(a+2,6),∴3a=(a+2)×6,∴a=-4,
∴反比例函数 的图像经过(-4,3),即k=-4×3=-12,∴反比例函数的表达式为 令y=-12,则
15.—1 [解析]化简,得
去分母,得x=3(x-1)+ mx,
移项、合并同类项,得(2+m)x=3,解得 由方程的解是正整数,得到x为正整数,
即2+m=1或2+m=3,解得m=--1或m=1(舍去,会使得分式无意义).
16.3b [解析]由数轴可知,b>0,a-b<0,a+b<0,∴原式=|b|+|a--b|--|a+b|=b--(a-b)+(a+b)=b--a+b+a+b=3b.
[解析]如图,过点 B 作 BH⊥AF 于点 H,连接EC交BM于点G.
∵正方形ABCD 的边长为1,点 M 是边CD 的中点,
∴BA=BC=CD=1,CM=
∵将△BCM 沿直线BM 翻折,点 C 与点 E 重合,
∴EC⊥BM,BE=BC=CD=1,CM=EM=
∵BH⊥AF,BE=BA=1,∴∠EBH= ∠EBA.
18. x>1或--4
即一次函数的表达式为
∵点(1,4)在反比例函数 的图像上,
解得 ,即反比例函数的表达式为
点((--4,-1)也在反比例函数的图像上.
结合题表可知,两图像的交点坐标为(-4,-1)和
(1,4),∴不等式 的解集是x>1或-4
(2)原式
20.(1)原式
当 时,原式
(2)原方程两边都乘(x+2)(x-2),
去分母,得3(x-2)+(x+2)(x-2)=x(x+2),
整理,得3x-10=2x,解得x=10,
检验:当x=10时,(x+2)(x-2)≠0,
故原方程的解为x=10.
21.(1)如图所示,△ADE 即为所求.
(2)如图,连接CE.
∵AB=AD,∠B=60°,
∴△ABD 是等边三角形,∴∠BAD=60°.
∵△ABC 旋转至△ADE,∴△ABC≌△ADE,
∴AC=AE,∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠CAE=∠BAD=60°,
∴△ACE 是等边三角形,∴CE=AE.
22.(1)8 40
(2)由(1)中计算,得
(3)在y=10x+20(0≤x≤8)中,令y=50,解得x=3;
在反比例函数 中,
令y=50,解得x=16.
∴饮水机的水温保持在50℃及以上的时间有16-3=13(分钟).
(4)不能.理由如下:
由题意可知,饮水机工作是以40分钟为一个循环,上午7:00 到上午第一节下课时(8:40)的时间是100分钟,是2个40分钟多20分钟,
∴学生上午第一节下课时(8:40)不能喝到超过50℃的水.
23.(1)∵反比例函数 和一次函数. 的图像相交于点A(-3,a)、B(a+ ,--2),
∴点A(-3,3)、B( ,-2),
把A(--3,3)、B( ,-2)代入 y= mx+n得 解得
(2)由图像可知,当. 时,自变量x的取值范围为-3
24.(1)∵DE⊥BC,
∴∠EDC=90°=∠CBA,∠DCE+∠DEC=90°.
在△ABC和△CDE 中
∴△ABC≌△CDE(SAS),
∴∠ACB=∠DEC,AC=CE,
∴∠ACB+∠DCE=∠ACE=90°,
∴△ACE 是等腰直角三角形.
(2)∵AB⊥BC,DE⊥BC,∴AB∥DF.
∵AB=CD,EF=CD,∴AB=EF,
∴四边形 AEFB 是平行四边形,
∴BF∥AE,∴∠BGC=∠AEC.
∵△ACE 是等腰直角三角形,
∴∠AEC=45°,∴∠BGC=∠AEC=45°.
25.(1)∵四边形ABCD 是正方形,
∴AD=AB,∠ADF=∠ABG=90°.
又DF=BG,∴△ADF≌△ABG(SAS).
∴∠DAF=∠BAG,AG=AF.
∴ ∠EAG = ∠BAG + ∠BAE = ∠DAF +
又AF=AG,AE=AE,
∴△AFE≌△AGE(SAS).
∴EF=EG=BE+BG=BE+DF.
(2)①当x=6时,CE=BC-BE=10-6=4,设DF=a,则CF=10-a,EF=BE+DF=6+a.在Rt△CEF中,由勾股定理,得 a) ,解得a=2.5.
②由(1),得.
描点画图如下:
(3)41.5 [解析]从图像可以看出y 的最小值约为8.29.∴△AEF 面积的最小值=△AEG 面积的最小值 8.29=41.45≈41.5.
[解析]∵AE+BG=2CF,
(2)选择小东的思路证明如下(答案不唯一):
∵n>1,∴n(n-1)(n+1)>0,
同课章节目录
