期末专题整合提优(二)中心对称图形——平行四边形(含答案)
文档属性
| 名称 | 期末专题整合提优(二)中心对称图形——平行四边形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 256.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 21:09:35 | ||
图片预览


文档简介
期末专题整合提优(二)中心对称图形——平行四边形
一、选择题
1.纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是( ).
2.已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( ).
A. 6 种 B. 5种
C. 4种 D. 3种
3.如图,在 Rt△ABC 中,∠ABC=90°,BF 是AC 边上的中线,DE 是△ABC 的中位线,若DE=10,则BF 的长为( ).
A. 10 B. 5 C. 8 D. 6
4.下列说法中错误的是().
A.两条对角线互相平分的四边形是平行四边形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直的矩形是正方形
D.两条对角线相等的菱形是正方形
5.如图,在矩形ABCD 中,若 AB=3,BC=4,EB∥DF 且 BE 与 DF 之间的距离为3,则AE 的长是( ).
A. B. C. D.
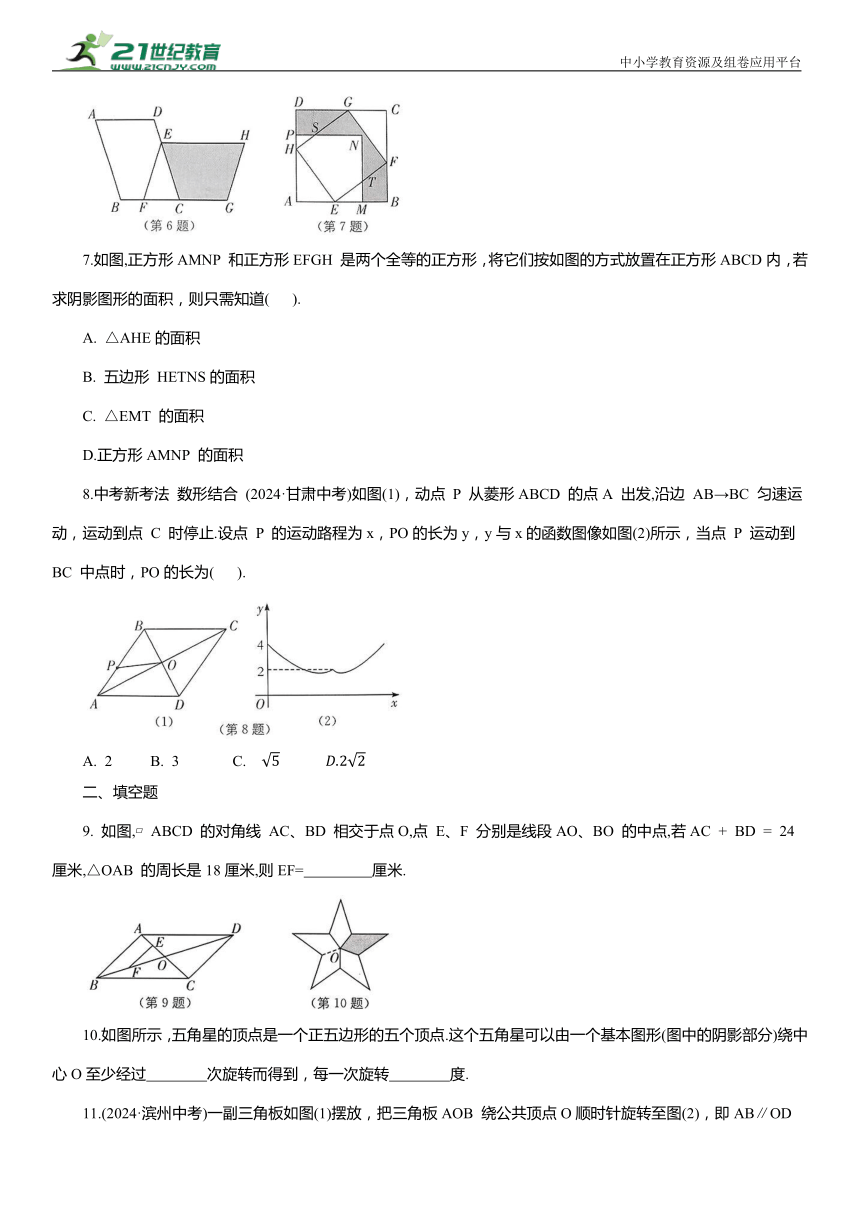
6.(2024·台湾中考)如图,平行四边形 ABCD 与平行四边形 EFGH 全等,且A、B、C、D的对应顶点分别是 H、E、F、G,其中点 E 在 DC 上,点 F在BC上,点C 在 FG 上.若AB=7,AD=5,FC=3,则四边形 ECGH 的周长为( ).
A. 21 B. 20 C. 19 D. 18
7.如图,正方形AMNP 和正方形EFGH 是两个全等的正方形,将它们按如图的方式放置在正方形ABCD内,若求阴影图形的面积,则只需知道( ).
A. △AHE的面积
B. 五边形 HETNS的面积
C. △EMT 的面积
D.正方形AMNP 的面积
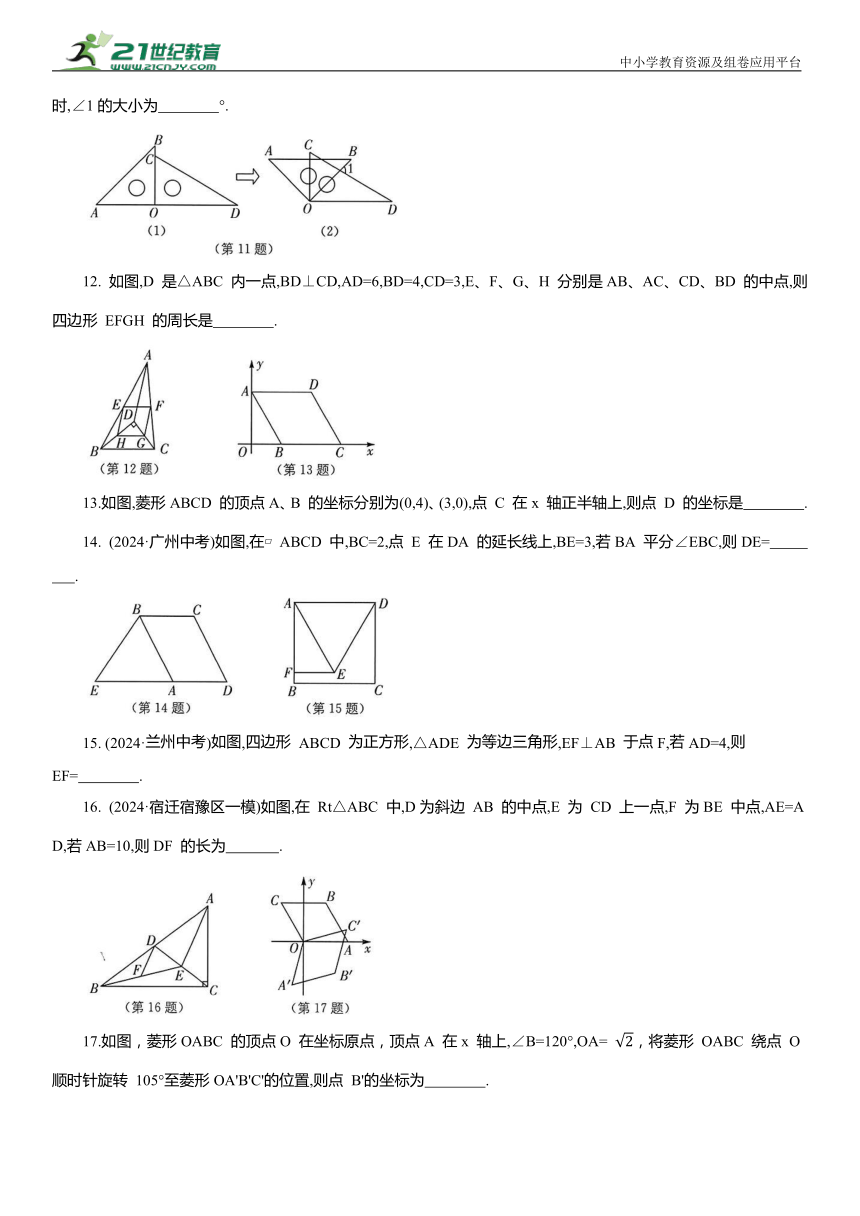
8.中考新考法 数形结合 (2024·甘肃中考)如图(1),动点 P 从菱形ABCD 的点A 出发,沿边 AB→BC 匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,PO的长为y,y与x的函数图像如图(2)所示,当点 P 运动到 BC 中点时,PO的长为( ).
A. 2 B. 3 C.
二、填空题
9. 如图, ABCD 的对角线 AC、BD 相交于点O,点 E、F 分别是线段AO、BO 的中点,若AC + BD = 24 厘米,△OAB 的周长是18厘米,则EF= 厘米.
中小学教育资源及组卷应用平台
10.如图所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过 次旋转而得到,每一次旋转 度.
11.(2024·滨州中考)一副三角板如图(1)摆放,把三角板AOB 绕公共顶点O顺时针旋转至图(2),即AB∥OD 时,∠1的大小为 °.
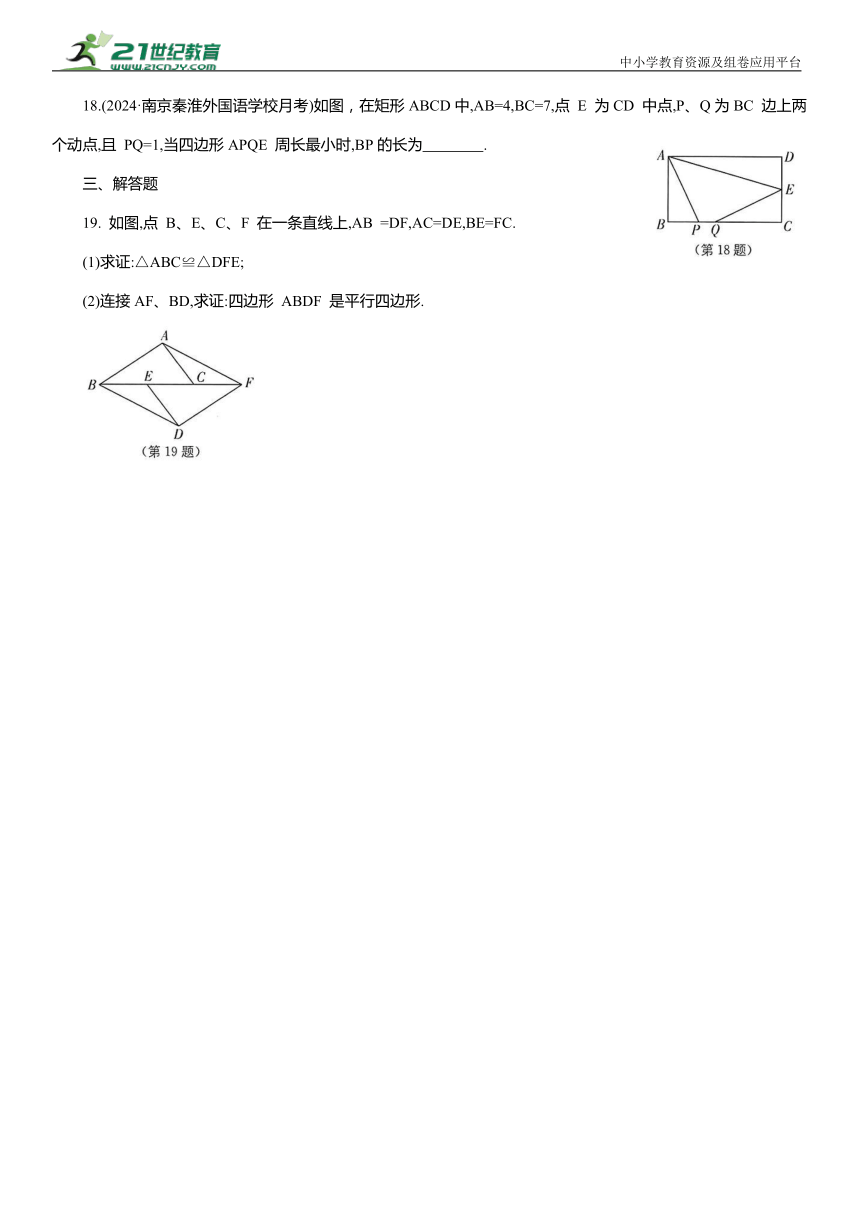
12. 如图,D 是△ABC 内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H 分别是AB、AC、CD、BD 的中点,则四边形 EFGH 的周长是 .
13.如图,菱形ABCD 的顶点A、B 的坐标分别为(0,4)、(3,0),点 C 在x 轴正半轴上,则点 D 的坐标是 .
14. (2024·广州中考)如图,在 ABCD 中,BC=2,点 E 在DA 的延长线上,BE=3,若BA 平分∠EBC,则DE= .
15. (2024·兰州中考)如图,四边形 ABCD 为正方形,△ADE 为等边三角形,EF⊥AB 于点F,若AD=4,则EF= .
16. (2024·宿迁宿豫区一模)如图,在 Rt△ABC 中,D为斜边 AB 的中点,E 为 CD 上一点,F 为BE 中点,AE=AD,若AB=10,则DF 的长为 .
17.如图,菱形OABC 的顶点O 在坐标原点,顶点A 在x 轴上,∠B=120°,OA= ,将菱形 OABC 绕点 O 顺时针旋转 105°至菱形OA'B'C'的位置,则点 B'的坐标为 .
18.(2024·南京秦淮外国语学校月考)如图,在矩形ABCD中,AB=4,BC=7,点 E 为CD 中点,P、Q为BC 边上两个动点,且 PQ=1,当四边形APQE 周长最小时,BP的长为 .
三、解答题
19. 如图,点 B、E、C、F 在一条直线上,AB =DF,AC=DE,BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形 ABDF 是平行四边形.
20.(2024·雅安中考)如图,点O 是□ABCD 对角线的交点,过点 O 的直线分别交 AD、BC 于点E、F.
(1)求证:△ODE≌△OBF;
(2)当 EF⊥BD 时,DE=15 cm,分别连接BE、DF.求此时四边形 BEDF 的周长.
21.(2023·随州中考)如图,矩形 ABCD 的对角线AC、BD 相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED 是菱形;
(2)若 BC=3,DC=2,求四边形OCED 的面积.
22.将三角形纸片ABC(AB>AC)沿过点 A 的直线折叠,使得 AC 落在边 AB 上,折痕为AD,展平纸片(如图(1));再次折叠该三角形纸片,使得点A 与点D 重合,折痕为 EF,再次展平后连接DE、DF(如图(2)).求证:四边形AEDF 是菱形.
23.如图,在四边形ABCD 中,AD∥BC,AB=AD,∠BAD的平分线AE 交BC 于点E,连接DE,AE与BD 交于点O.
(1)求证:四边形 ABED 是菱形;
(2)若( 求AB 的长.
24.将矩形ABCD 绕点A 顺时针旋转 360°),得到矩形AEFG.
(1)如图,当点 E 在BD 上时,求证:FD=CD.
(2)当α为何值时,GC=GB 画出图形,并说明理由.
25.如图,在 Rt△ABC 中,∠B=90°,BC=5 ∠C=30°.点 D 从点C 出发沿CA 方向以每秒2个单位长度的速度向点 A 匀速运动,同时点 E 从点 A 出发沿AB 方向以每秒1个单位长度的速度向点 B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点 D、E 运动的时间是t秒(t>0).过点 D作DF⊥BC 于点F,连接DE、EF.
(1)求证:AE=DF.
(2)四边形 AEFD 能够成为菱形吗 如果能,求出相应的t值;如果不能,说明理由.
(3)当 t 为何值时,△DEF 为直角三角形 请说明理由.
26.题(1)来自于课本中的习题,请你完成解答,提炼方法并完成题(2).
(1)如图(1),在△ABC 中,BD 平分∠ABC,交AC 于点 D,过点D 作BC 的平行线,交AB 于点 E,请判断△BDE 的形状,并说明理由.
[方法应用]
(2)如图(2),在 ABCD 中,BE 平分∠ABC,交边AD于点E,过点 A 作AF⊥BE 交DC的延长线于点 F,交 BC 于点G.
①图中一定是等腰三角形的有( );
A. 3 个 B. 4 个 C. 5个 D. 6个
②已知AB=3,BC=5,求CF 的长.
1. B 2. C
3. A [解析]∵DE 是△ABC的中位线,DE=10,∴AC=2DE=20.
在Rt△ABC 中,∠ABC=90°,BF 是边AC 上的中线,则 故选 A.
4. B
5. C [解析]过点 E 作EH⊥DF 于点 H,则EH=AB=3,∠A=∠EHD=90°.
∵EB∥DF,∴∠EDH=∠AEB.
∴易证△AEB≌△HDE.∴DE=BE,DH=AE.
在Rt△AEB中,设AE=x,则BE=DE=4-x,则 解得 故选C.
6. A [解析]∵平行四边形 ABCD 与平行四边形EFGH 全等,且A、B、C、D 的对应顶点分别是H、E、F、G,∴AB=CD=HE=FG=7,AD=HG=EF=5,∠DCB=∠GFE,∴EF=EC=5.
∵FC=3,∴CG=FG-FC=4,
∵四边形 ECGH 的周长=EC+CG+HG+EH=5+4+5+7=21.故选 A.
7. A [解析]∵正方形 AMNP 和正方形EFGH 是两个全等的正方形,∴正方形AMNP 的面积=正方形EFGH 的面积,∴正方形AMNP 的面积-五边形HETNS 的面积=正方形 EFGH 的面积-五边形HETNS 的面积,∴阴影部分的面积=△DGH 的面积+△AHE 的面积+△BEF 的面积.
在正方形ABCD 中,∠A=∠D=90°,
∴∠AHE+∠AEH=90°.
在正方形 HEFG中,HE=HG,∠GHE=90°,
∴∠AHE+∠DHG=90°,∴∠AEH=∠DHG,
∴易证△AHE≌△DGH(AAS),
∴△AHE 的面积=△DGH 的面积.同理可得△AHE≌△BEF(AAS),
∴△AHE 的面积=△BEF 的面积,
∴阴影部分的面积=3S△AHE.
∴只要知道△AHE 的面积即可求出阴影部分的面积.故选 A.
8. C [解析]结合图像,得到当x=0时,PO=AO=4,当点 P 运动到点 B 时,PO=BO=2.
∵在菱形 ABCD 中,AC⊥BD,∴∠AOB=∠BOC=
当点 P 运动到BC中点时,PO 的长为 故选 C.
9.3 [解析]∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AC+BD=24厘米,∴OA+OB=12厘米.
∵△OAB 的周长是18厘米,∴AB=6厘米.
∵点E、F 分别是线段AO、BO的中点,
∴EF 是△OAB 的中位线, 厘米.
10.4 72
11.75 [解析]由已知可得,∠B=45°,∠D=30°.
∵AB∥OD,∴∠B=∠BOD=45°.
12.11
13.(5,4) [解析]∵菱形ABCD的顶点A(0,4)、B(3,0),∴OA=4,OB=3.
∵四边形ABCD 是菱形,∴AB=AD=5.
∴D(5,4).
14.5 [解析]∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC=2,∴∠EAB=∠CBA.
∵BA平分∠EBC,∴∠EBA=∠CBA,
∴∠EAB=∠EBA,∴AE=BE=3,
∴DE=AD+AE=2+3=5.
15.2 16. 17.(1,-1)
18.4 [解析]∵四边形ABCD 是矩形,AB=4,BC=7,PQ=1,点 E为CD中点,∴AE 为定长,∴四边形APQE 周长最小时,即AP+EQ最小,取AB 中点F,连接EF,在EF 上取. 连接E'P.
则四边形 BCEF 为矩形,四边形 EE'PQ 为平行四边形,
∴E'P=EQ,∴AP+EQ=AP+E'P,
∴AP+EQ最小,即 AP+E'P 最小即可,作点A 关于BC 的对称点A',连接E'A'交 BC 于点P',则
即AP+E'P 最小时,点 P 位于P'处,
∴BP'的长即为所求.
4+2=6,∴△A'E'F是等腰直角三角形,
19.(1)∵BE=FC,∴BC=FE.
在△ABC 和△DFE 中,
∴△ABC≌△DFE(SSS).
(2)由(1)知△ABC≌△DFE,∴∠ABC=∠DFE.∴AB∥DF.又AB=DF,∴四边形ABDF 是平行四边形.
20.(1)∵四边形ABCD 是平行四边形, ∴AD∥CB,∴∠OED=∠OFB.
∵点O是 ABCD对角线的交点,∴OD=OB.
在△ODE 和△OBF 中,
∴△ODE≌△OBF(AAS).
(2)连接BE、DF,
由(1)得△ODE≌△OBF,∴DE=BF.
∵DE∥BF,∴四边形BEDF 是平行四边形.
∵EF⊥BD,∴四边形 BEDF 是菱形.
∴DF=BF=BE=DE=15cm,
∴DF+BF+BE+DE=4DE=4×15=60(cm),
∴四边形 BEDF 的周长为60cm.
21.(1)∵DE∥AC,CE∥BD,
∴四边形OCED 是平行四边形.
∵矩形ABCD 的对角线AC、BD 相交于点O,
∴OC=OD,∴四边形OCED 是菱形.
(2)∵四边形ABCD 是矩形,BC=3,DC=2,
∴OA=OB=OC=OD,S矩形ABCD=3×2=6,
∵四边形OCED 是菱形,
∴菱形OCED的面积==2S△OCD=2×1.5=3.
22.∵三角形纸片ABC(AB>AC)沿过点 A 的直线折叠,使得AC落在边AB 上,折痕为AD,
∴∠BAD=∠CAD.
又点 A 与点D 重合,折痕为EF,
∴AE=ED,AF=FD.
∴∠EAD=∠EDA=∠FAD=∠ADF.
在△AED 和△AFD中
∴△AED≌△AFD(ASA).
∴AE=AF=ED=FD.
∴四边形AEDF 是菱形.
23.(1)∵AE平分∠BAD,∴∠BAE=∠DAE.
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),∴BE=DE.
∵AD∥BC,∴∠DAE=∠AEB=∠BAE,
∴AB=BE,∴AB=BE=DE=AD.
∴四边形 ABED 是菱形.
(2)由(1)知,四边形ABED 是菱形,
∵2∠C=60°,∴∠C=30°,∴∠DBC=∠C.
在Rt△OAB中,∠AOB=90°,∠ABO=30°,
∴AB=2.
24.(1)由旋转的性质可得AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE.
又
∴∠EDA=∠DEF.
又DE=ED,AD=EF,
∴△AED≌△FDE(SAS),∴AE=FD.
又AE=AB=CD,∴FD=CD.
(2)当α=60°或300°时,GC=GB.理由如下:
当GC=GB时,点G在BC的垂直平分线上.
分两种情况讨论:
①当点G在AD 右侧时,取 BC 的中点 H,连接GH交AD 于点M,连接GB、GC、GD,如图(1).
∵GC=GB,CH=BH,∴GH⊥BC,
∴四边形 ABHM 是矩形,
∴GM 垂直平分AD,∴GD=GA=AD,
∴△ADG 是等边三角形,
∴∠DAG=60°,∴旋转角α=60°.
②当点G在AD 左侧时,如图(2),同理可得△ADG是等边三角形,∴∠DAG=60°,
∴旋转角(
综上, 或300°时,GB=GC.
25.(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF=t.又AE=t,∴AE=DF.
(2)能.理由如下:
∵AB⊥BC,DF⊥BC,∴AE∥DF.
又AE=DF,∴四边形AEFD为平行四边形.
在 Rt△ABC中,
∴AB=5,AC=10.
∴AD=AC-DC=10-2t.
若使 AEFD为菱形,则需AE=AD, 即t=10-2t,解得
即当 时,四边形AEFD 为菱形.
(3)①当∠EDF=90°时,四边形EBFD 为矩形.
在 Rt△AED 中,∠ADE=∠C=30°,
∴AD=2AE,即10-2t=2t,解得
②当∠DEF=90°时,由(2)四边形 AEFD 为平行四边形知EF∥AD,∴∠ADE=∠DEF=90°.
即 解得t=4;
③当∠EFD=90°时,此种情况不存在.
综上所述,当 或4时,△DEF 为直角三角形.
26.(1)△BDE 的形状是等腰三角形.理由如下:
∵BD平分∠ABC,∴∠ABD=∠CBD.
∵BC∥ED,∴∠EDB=∠CBD,
∴∠EDB=∠ABD,∴EB=ED,
∴△BDE 是等腰三角形.
(2)①B [解析]共有四个等腰三角形.分别是△ABE、△ABG、△AFD、△CGF.
②由(1)易知,∠ABE=∠EBG=∠AEB.
AB=AE=3.
∵AF⊥BE,∴∠BAF=∠EAF.
∵BC∥AD,∴∠EAG=∠AGB,
∴∠BAF=∠AGB,∴AB=BG=3.
∵AB∥FD,∴∠BAF=∠CFG.
∵∠AGB=∠CGF,∴∠CGF=∠CFG,
∴CG=CF.
∵CG=BC-BG=5-3=2,∴CF=2.
一、选择题
1.纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是( ).
2.已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( ).
A. 6 种 B. 5种
C. 4种 D. 3种
3.如图,在 Rt△ABC 中,∠ABC=90°,BF 是AC 边上的中线,DE 是△ABC 的中位线,若DE=10,则BF 的长为( ).
A. 10 B. 5 C. 8 D. 6
4.下列说法中错误的是().
A.两条对角线互相平分的四边形是平行四边形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直的矩形是正方形
D.两条对角线相等的菱形是正方形
5.如图,在矩形ABCD 中,若 AB=3,BC=4,EB∥DF 且 BE 与 DF 之间的距离为3,则AE 的长是( ).
A. B. C. D.
6.(2024·台湾中考)如图,平行四边形 ABCD 与平行四边形 EFGH 全等,且A、B、C、D的对应顶点分别是 H、E、F、G,其中点 E 在 DC 上,点 F在BC上,点C 在 FG 上.若AB=7,AD=5,FC=3,则四边形 ECGH 的周长为( ).
A. 21 B. 20 C. 19 D. 18
7.如图,正方形AMNP 和正方形EFGH 是两个全等的正方形,将它们按如图的方式放置在正方形ABCD内,若求阴影图形的面积,则只需知道( ).
A. △AHE的面积
B. 五边形 HETNS的面积
C. △EMT 的面积
D.正方形AMNP 的面积
8.中考新考法 数形结合 (2024·甘肃中考)如图(1),动点 P 从菱形ABCD 的点A 出发,沿边 AB→BC 匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,PO的长为y,y与x的函数图像如图(2)所示,当点 P 运动到 BC 中点时,PO的长为( ).
A. 2 B. 3 C.
二、填空题
9. 如图, ABCD 的对角线 AC、BD 相交于点O,点 E、F 分别是线段AO、BO 的中点,若AC + BD = 24 厘米,△OAB 的周长是18厘米,则EF= 厘米.
中小学教育资源及组卷应用平台
10.如图所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过 次旋转而得到,每一次旋转 度.
11.(2024·滨州中考)一副三角板如图(1)摆放,把三角板AOB 绕公共顶点O顺时针旋转至图(2),即AB∥OD 时,∠1的大小为 °.
12. 如图,D 是△ABC 内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H 分别是AB、AC、CD、BD 的中点,则四边形 EFGH 的周长是 .
13.如图,菱形ABCD 的顶点A、B 的坐标分别为(0,4)、(3,0),点 C 在x 轴正半轴上,则点 D 的坐标是 .
14. (2024·广州中考)如图,在 ABCD 中,BC=2,点 E 在DA 的延长线上,BE=3,若BA 平分∠EBC,则DE= .
15. (2024·兰州中考)如图,四边形 ABCD 为正方形,△ADE 为等边三角形,EF⊥AB 于点F,若AD=4,则EF= .
16. (2024·宿迁宿豫区一模)如图,在 Rt△ABC 中,D为斜边 AB 的中点,E 为 CD 上一点,F 为BE 中点,AE=AD,若AB=10,则DF 的长为 .
17.如图,菱形OABC 的顶点O 在坐标原点,顶点A 在x 轴上,∠B=120°,OA= ,将菱形 OABC 绕点 O 顺时针旋转 105°至菱形OA'B'C'的位置,则点 B'的坐标为 .
18.(2024·南京秦淮外国语学校月考)如图,在矩形ABCD中,AB=4,BC=7,点 E 为CD 中点,P、Q为BC 边上两个动点,且 PQ=1,当四边形APQE 周长最小时,BP的长为 .
三、解答题
19. 如图,点 B、E、C、F 在一条直线上,AB =DF,AC=DE,BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形 ABDF 是平行四边形.
20.(2024·雅安中考)如图,点O 是□ABCD 对角线的交点,过点 O 的直线分别交 AD、BC 于点E、F.
(1)求证:△ODE≌△OBF;
(2)当 EF⊥BD 时,DE=15 cm,分别连接BE、DF.求此时四边形 BEDF 的周长.
21.(2023·随州中考)如图,矩形 ABCD 的对角线AC、BD 相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED 是菱形;
(2)若 BC=3,DC=2,求四边形OCED 的面积.
22.将三角形纸片ABC(AB>AC)沿过点 A 的直线折叠,使得 AC 落在边 AB 上,折痕为AD,展平纸片(如图(1));再次折叠该三角形纸片,使得点A 与点D 重合,折痕为 EF,再次展平后连接DE、DF(如图(2)).求证:四边形AEDF 是菱形.
23.如图,在四边形ABCD 中,AD∥BC,AB=AD,∠BAD的平分线AE 交BC 于点E,连接DE,AE与BD 交于点O.
(1)求证:四边形 ABED 是菱形;
(2)若( 求AB 的长.
24.将矩形ABCD 绕点A 顺时针旋转 360°),得到矩形AEFG.
(1)如图,当点 E 在BD 上时,求证:FD=CD.
(2)当α为何值时,GC=GB 画出图形,并说明理由.
25.如图,在 Rt△ABC 中,∠B=90°,BC=5 ∠C=30°.点 D 从点C 出发沿CA 方向以每秒2个单位长度的速度向点 A 匀速运动,同时点 E 从点 A 出发沿AB 方向以每秒1个单位长度的速度向点 B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点 D、E 运动的时间是t秒(t>0).过点 D作DF⊥BC 于点F,连接DE、EF.
(1)求证:AE=DF.
(2)四边形 AEFD 能够成为菱形吗 如果能,求出相应的t值;如果不能,说明理由.
(3)当 t 为何值时,△DEF 为直角三角形 请说明理由.
26.题(1)来自于课本中的习题,请你完成解答,提炼方法并完成题(2).
(1)如图(1),在△ABC 中,BD 平分∠ABC,交AC 于点 D,过点D 作BC 的平行线,交AB 于点 E,请判断△BDE 的形状,并说明理由.
[方法应用]
(2)如图(2),在 ABCD 中,BE 平分∠ABC,交边AD于点E,过点 A 作AF⊥BE 交DC的延长线于点 F,交 BC 于点G.
①图中一定是等腰三角形的有( );
A. 3 个 B. 4 个 C. 5个 D. 6个
②已知AB=3,BC=5,求CF 的长.
1. B 2. C
3. A [解析]∵DE 是△ABC的中位线,DE=10,∴AC=2DE=20.
在Rt△ABC 中,∠ABC=90°,BF 是边AC 上的中线,则 故选 A.
4. B
5. C [解析]过点 E 作EH⊥DF 于点 H,则EH=AB=3,∠A=∠EHD=90°.
∵EB∥DF,∴∠EDH=∠AEB.
∴易证△AEB≌△HDE.∴DE=BE,DH=AE.
在Rt△AEB中,设AE=x,则BE=DE=4-x,则 解得 故选C.
6. A [解析]∵平行四边形 ABCD 与平行四边形EFGH 全等,且A、B、C、D 的对应顶点分别是H、E、F、G,∴AB=CD=HE=FG=7,AD=HG=EF=5,∠DCB=∠GFE,∴EF=EC=5.
∵FC=3,∴CG=FG-FC=4,
∵四边形 ECGH 的周长=EC+CG+HG+EH=5+4+5+7=21.故选 A.
7. A [解析]∵正方形 AMNP 和正方形EFGH 是两个全等的正方形,∴正方形AMNP 的面积=正方形EFGH 的面积,∴正方形AMNP 的面积-五边形HETNS 的面积=正方形 EFGH 的面积-五边形HETNS 的面积,∴阴影部分的面积=△DGH 的面积+△AHE 的面积+△BEF 的面积.
在正方形ABCD 中,∠A=∠D=90°,
∴∠AHE+∠AEH=90°.
在正方形 HEFG中,HE=HG,∠GHE=90°,
∴∠AHE+∠DHG=90°,∴∠AEH=∠DHG,
∴易证△AHE≌△DGH(AAS),
∴△AHE 的面积=△DGH 的面积.同理可得△AHE≌△BEF(AAS),
∴△AHE 的面积=△BEF 的面积,
∴阴影部分的面积=3S△AHE.
∴只要知道△AHE 的面积即可求出阴影部分的面积.故选 A.
8. C [解析]结合图像,得到当x=0时,PO=AO=4,当点 P 运动到点 B 时,PO=BO=2.
∵在菱形 ABCD 中,AC⊥BD,∴∠AOB=∠BOC=
当点 P 运动到BC中点时,PO 的长为 故选 C.
9.3 [解析]∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AC+BD=24厘米,∴OA+OB=12厘米.
∵△OAB 的周长是18厘米,∴AB=6厘米.
∵点E、F 分别是线段AO、BO的中点,
∴EF 是△OAB 的中位线, 厘米.
10.4 72
11.75 [解析]由已知可得,∠B=45°,∠D=30°.
∵AB∥OD,∴∠B=∠BOD=45°.
12.11
13.(5,4) [解析]∵菱形ABCD的顶点A(0,4)、B(3,0),∴OA=4,OB=3.
∵四边形ABCD 是菱形,∴AB=AD=5.
∴D(5,4).
14.5 [解析]∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC=2,∴∠EAB=∠CBA.
∵BA平分∠EBC,∴∠EBA=∠CBA,
∴∠EAB=∠EBA,∴AE=BE=3,
∴DE=AD+AE=2+3=5.
15.2 16. 17.(1,-1)
18.4 [解析]∵四边形ABCD 是矩形,AB=4,BC=7,PQ=1,点 E为CD中点,∴AE 为定长,∴四边形APQE 周长最小时,即AP+EQ最小,取AB 中点F,连接EF,在EF 上取. 连接E'P.
则四边形 BCEF 为矩形,四边形 EE'PQ 为平行四边形,
∴E'P=EQ,∴AP+EQ=AP+E'P,
∴AP+EQ最小,即 AP+E'P 最小即可,作点A 关于BC 的对称点A',连接E'A'交 BC 于点P',则
即AP+E'P 最小时,点 P 位于P'处,
∴BP'的长即为所求.
4+2=6,∴△A'E'F是等腰直角三角形,
19.(1)∵BE=FC,∴BC=FE.
在△ABC 和△DFE 中,
∴△ABC≌△DFE(SSS).
(2)由(1)知△ABC≌△DFE,∴∠ABC=∠DFE.∴AB∥DF.又AB=DF,∴四边形ABDF 是平行四边形.
20.(1)∵四边形ABCD 是平行四边形, ∴AD∥CB,∴∠OED=∠OFB.
∵点O是 ABCD对角线的交点,∴OD=OB.
在△ODE 和△OBF 中,
∴△ODE≌△OBF(AAS).
(2)连接BE、DF,
由(1)得△ODE≌△OBF,∴DE=BF.
∵DE∥BF,∴四边形BEDF 是平行四边形.
∵EF⊥BD,∴四边形 BEDF 是菱形.
∴DF=BF=BE=DE=15cm,
∴DF+BF+BE+DE=4DE=4×15=60(cm),
∴四边形 BEDF 的周长为60cm.
21.(1)∵DE∥AC,CE∥BD,
∴四边形OCED 是平行四边形.
∵矩形ABCD 的对角线AC、BD 相交于点O,
∴OC=OD,∴四边形OCED 是菱形.
(2)∵四边形ABCD 是矩形,BC=3,DC=2,
∴OA=OB=OC=OD,S矩形ABCD=3×2=6,
∵四边形OCED 是菱形,
∴菱形OCED的面积==2S△OCD=2×1.5=3.
22.∵三角形纸片ABC(AB>AC)沿过点 A 的直线折叠,使得AC落在边AB 上,折痕为AD,
∴∠BAD=∠CAD.
又点 A 与点D 重合,折痕为EF,
∴AE=ED,AF=FD.
∴∠EAD=∠EDA=∠FAD=∠ADF.
在△AED 和△AFD中
∴△AED≌△AFD(ASA).
∴AE=AF=ED=FD.
∴四边形AEDF 是菱形.
23.(1)∵AE平分∠BAD,∴∠BAE=∠DAE.
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),∴BE=DE.
∵AD∥BC,∴∠DAE=∠AEB=∠BAE,
∴AB=BE,∴AB=BE=DE=AD.
∴四边形 ABED 是菱形.
(2)由(1)知,四边形ABED 是菱形,
∵2∠C=60°,∴∠C=30°,∴∠DBC=∠C.
在Rt△OAB中,∠AOB=90°,∠ABO=30°,
∴AB=2.
24.(1)由旋转的性质可得AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE.
又
∴∠EDA=∠DEF.
又DE=ED,AD=EF,
∴△AED≌△FDE(SAS),∴AE=FD.
又AE=AB=CD,∴FD=CD.
(2)当α=60°或300°时,GC=GB.理由如下:
当GC=GB时,点G在BC的垂直平分线上.
分两种情况讨论:
①当点G在AD 右侧时,取 BC 的中点 H,连接GH交AD 于点M,连接GB、GC、GD,如图(1).
∵GC=GB,CH=BH,∴GH⊥BC,
∴四边形 ABHM 是矩形,
∴GM 垂直平分AD,∴GD=GA=AD,
∴△ADG 是等边三角形,
∴∠DAG=60°,∴旋转角α=60°.
②当点G在AD 左侧时,如图(2),同理可得△ADG是等边三角形,∴∠DAG=60°,
∴旋转角(
综上, 或300°时,GB=GC.
25.(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF=t.又AE=t,∴AE=DF.
(2)能.理由如下:
∵AB⊥BC,DF⊥BC,∴AE∥DF.
又AE=DF,∴四边形AEFD为平行四边形.
在 Rt△ABC中,
∴AB=5,AC=10.
∴AD=AC-DC=10-2t.
若使 AEFD为菱形,则需AE=AD, 即t=10-2t,解得
即当 时,四边形AEFD 为菱形.
(3)①当∠EDF=90°时,四边形EBFD 为矩形.
在 Rt△AED 中,∠ADE=∠C=30°,
∴AD=2AE,即10-2t=2t,解得
②当∠DEF=90°时,由(2)四边形 AEFD 为平行四边形知EF∥AD,∴∠ADE=∠DEF=90°.
即 解得t=4;
③当∠EFD=90°时,此种情况不存在.
综上所述,当 或4时,△DEF 为直角三角形.
26.(1)△BDE 的形状是等腰三角形.理由如下:
∵BD平分∠ABC,∴∠ABD=∠CBD.
∵BC∥ED,∴∠EDB=∠CBD,
∴∠EDB=∠ABD,∴EB=ED,
∴△BDE 是等腰三角形.
(2)①B [解析]共有四个等腰三角形.分别是△ABE、△ABG、△AFD、△CGF.
②由(1)易知,∠ABE=∠EBG=∠AEB.
AB=AE=3.
∵AF⊥BE,∴∠BAF=∠EAF.
∵BC∥AD,∴∠EAG=∠AGB,
∴∠BAF=∠AGB,∴AB=BG=3.
∵AB∥FD,∴∠BAF=∠CFG.
∵∠AGB=∠CGF,∴∠CGF=∠CFG,
∴CG=CF.
∵CG=BC-BG=5-3=2,∴CF=2.
同课章节目录
