第12 章二次根式提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 第12 章二次根式提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 172.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 04:49:59 | ||
图片预览


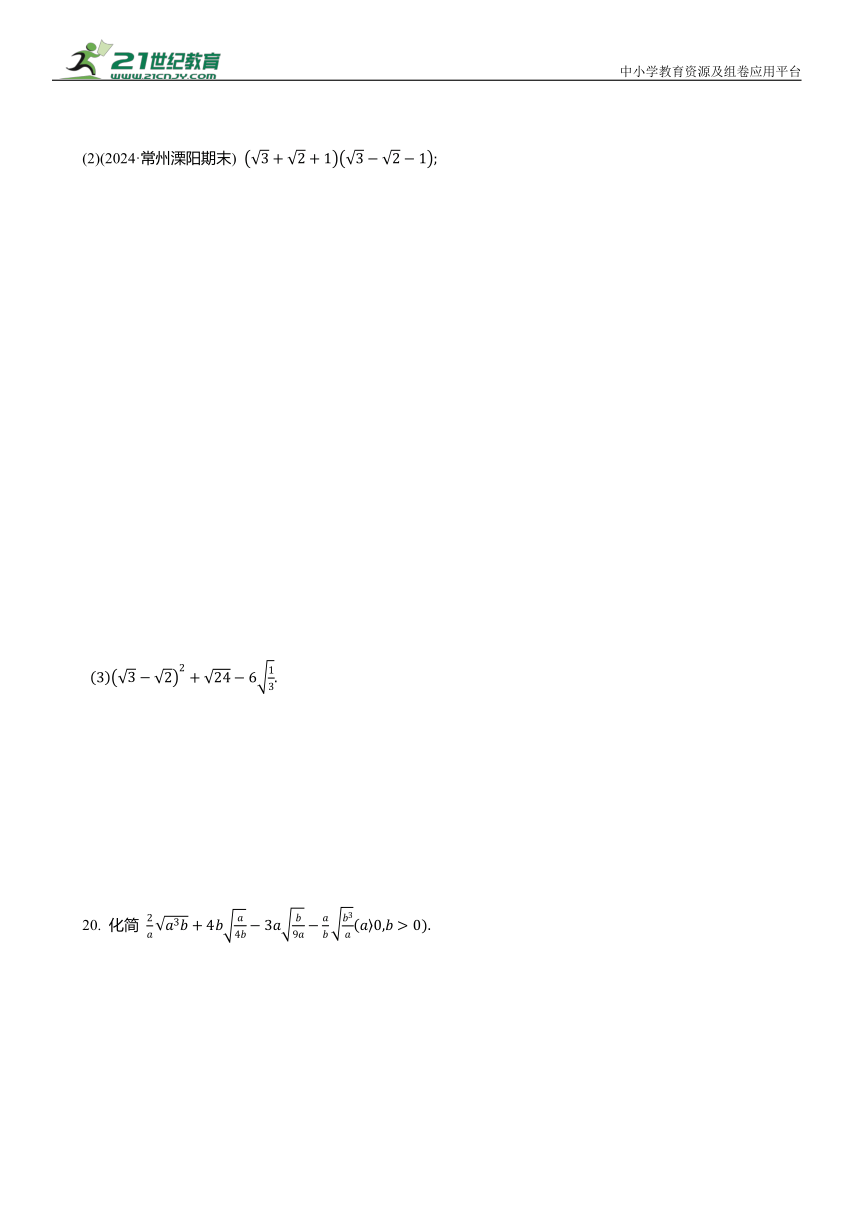


文档简介
中小学教育资源及组卷应用平台
第12 章二次根式提优测评卷
时间:90分钟 总分:100分
第Ⅰ卷(选择题 共16分)
一、选择题(每题2分,共16分)
1.下列根式中属于最简二次根式的是( ).
B. C.
2.下列各组二次根式中,是同类二次根式的是( ).
B. 与
3.(2024·扬州期末)下列运算正确的是( ).
4.已知一把木质三角尺的斜边长为60cm,其中一条直角边的长为30cm,则另一条直角边的长为( ).
D. 30 cm
5.小明在学习中发现了一个有趣的现象:
)
上面的推导过程中,错误的步骤开始出现在( ).
A. 第①步 B. 第②步 C. 第③步 D. 第④步
6. (2024·重庆中考B卷)估计 的值应在( ).
A. 8和9之间 B. 9和10之间 C. 10和11之间 D. 11和12之间
7.实数a 在数轴上的位置如图所示,则 化简后为( ).
A. 7 B. - 7 C. 2a-15 D.无法确定
8.已知 且a>b>0,则 的值是( ).
A. B. C. D.
第Ⅱ卷(非选择题 共84分)
二、填空题(每题3分,共30分)
9.(2024·南京玄武区二模)若式子 在实数范围内有意义,则x的取值范围是 .
10.请写出一个正整数m的值使得 m是整数:m=
11.(2024·扬州仪征一模)已知实数a 满足条件 那么a-2023 的值为 .
12. 用“<”把下列各数连接起来:—3 、3.14、π、-0.13、——2 : .
13. 已知xy<0,化简:
14. 如果 那么a 的取值范围是 .
15.已知三角形三边分别为 则它的周长为 cm.
16. (2024·连云港连云区模拟)若 则a的值为 .
17. 若x、y为实数,且| 则 的值为 .
18. 已知 当x分别取1、2、3、…、2024时,所对应y值的总和是 .
三、解答题(第19~22题每题6分,第23、24题每题7分,第25、26题每题8分,共54分)
19. 计算:
(1)(2024·镇江丹徒区期末)
(2)(2024·常州溧阳期末)
20. 化简
21. 如图,在平面直角坐标系中,点A、B 的坐标分别为A(a,0)、B(b,0),且a、b满足 点C的坐标为(0,3).
(1)求a、b的值及
(2)若点M在x轴上,且 试求点 M 的坐标.
22.先阅读下列材料,再解决问题:
阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去一层根号.例如:
解决问题:
(1)模仿上例的过程填空:
(2)根据上述思路,试将下列二次根式化简
23.(2024·宿迁宿城区期末)[再读教材]我们八年级下册数学课本第161页介绍了“海伦——秦九韶公式”:如果一个三角形的三边长分别为a、b、c,记 那么三角形的面积为
[解决问题]如图,在 中,
(1)请你用“海伦一秦九韶公式”求 的面积.
(2)除了利用“海伦—秦九韶公式”求 的面积外,你还有其他的解法吗 请写出你的解法.
24. 像( ·两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.
(1)请写出以下代数式的一个有理化因式:
(2)化简
(3)当 时,直接写出代数式 的最大值: .
25.(2024·甘肃武威凉州区期末)如图,小明家有一块长方形空地ABCD,长BC为 宽AB为 ,现要在空地中挖一个长方形的水池(即图中阴影部分),其余部分种植草莓.其中长方形水池的长为 宽为
(1)求长方形空地ABCD的周长.(结果化为最简二次根式)
(2)已知小明家种植的草莓售价为8元/千克,且每平方米产草莓15千克,若小明家将所种的草莓全部销售完,销售收入为多少元
26.(2024·南通通州区育才中学月考)规定:关于x、y的二元一次方程 有无数组解,每组解记为P(x,y),称点P(x,y)为“坐标点”,将这些“坐标点”连接新得到一条直线,称这条直线是“坐标点”的“关联线”,回答下列问题:
(1)已知 ),则是“关联线 的“坐标点”的是 ;
(2)若A(1,1)、B(4,-1)是“关联线 的“坐标点”,求a、b的值;
(3)已如m、n 是实数,且 若 是“关联线 的一个“坐标点”,用等式表示s 与m之间的关系,并求出s 的最小值.
1. A
2. D [解析] 与 不是同类二次根式,故A 不符合题意;] 与 不是同类二次根式,故B不符合题意;C. 不是同类二次根式,故C不符合题意;I 与 是同类二次根式,故D符合题意.故选D.
3. D [解析] 不是同类二次根式,不能合并,此选项不合题意; 此选项不合题意; 此选项不合题意; 此选项符合题意.故选 D.
4. C [解析]由题意,得另一条直角边的长为 故选C.
5. B
6. C [解析] 而 故选C.
7. A [解析]由数轴,得5故原式==a-4+11-a=7.故选 A.
8. D [解析]∵
即
同理可得
故选 D.
9. x≤5 [解析]由题意,得5-x≥0,解得x≤5.
10.2(答案不唯一)
11.2024 [解析].
∴a-2024≥0,即a≥2024,∴2023-a<0,
[解析]∵二次根式 有意义,∴y<0.∵xy<0,∴x>0.
14.-316.18 [解析]由题意,得a-2≥0,解得a≥2, 16,解得a=18.
17.1
18.16186 [解析]由题意,得.y=x+5--|x-3|,当x≤3时,y=x+5+x-3=2x+2,当x>3时,y=x+5-(x-3)=x+5-x+3=8,∴y值的总和为4+6+8+8+8+…+8=4+6+8×2022=16186.
19.(1)9 (2)-2
21.(1)∵a、b满足( ∴b=4,a=-1,∴A(-1,0)、B(4,0),
(2)设M 的坐标为(m,0),
∴当 时, 当 时,
∴符合条件的点M的坐标为(( ,0)和(
(2)原式
23.(1)∵三角形三边长分别为4、5、7,
(2)有其他的解法.解法如下:
过点C 作 CH⊥AB 于点 H,设 AH=x,则 BH=7-x,
在Rt△ACH 中,
在Rt△BCH 中,
解得
在Rt△ACH 中,
(答案不唯一)
(2)原式
[解析 ] ∴当 a =2 时, 有最小值,最小值为 此时 的值最大,最大值为
故代数式 的最大值为
方法诠释 要求 的最大值,是很困难的,但我们可以逆用分母有理化也就是分子有理化,可得 而 在自变量的取值范围内是可以求出它的最小值的.
25.(1)长方形空地ABCD的周长:
故长方形空地 ABCD 的周长为
(2)种草莓的面积为
39×15×8=4680(元).
故销售收入为4680元.
26.(1)P (-1,3) [解析]由于 P (--1,3)是二元一次方程x+y=2的解,而P (4,-1)、P (1,2)不是二元一次方程x+y=2的解,
∴“关联线” x+y=2的“坐标点”的是P (-1,3).
(2)∵A(1,1)、B(4,-1)是“关联线”(a+1)x+by=5的“坐标点”,
解得
∴a=1,b=3.
是“关联线’” 5x-2y=s的一个“坐标点”,
即s-3≥0,∴s≥3,
∴s的最小值为3.
故s 与m 之间的关系为 s的最小值是3.
第12 章二次根式提优测评卷
时间:90分钟 总分:100分
第Ⅰ卷(选择题 共16分)
一、选择题(每题2分,共16分)
1.下列根式中属于最简二次根式的是( ).
B. C.
2.下列各组二次根式中,是同类二次根式的是( ).
B. 与
3.(2024·扬州期末)下列运算正确的是( ).
4.已知一把木质三角尺的斜边长为60cm,其中一条直角边的长为30cm,则另一条直角边的长为( ).
D. 30 cm
5.小明在学习中发现了一个有趣的现象:
)
上面的推导过程中,错误的步骤开始出现在( ).
A. 第①步 B. 第②步 C. 第③步 D. 第④步
6. (2024·重庆中考B卷)估计 的值应在( ).
A. 8和9之间 B. 9和10之间 C. 10和11之间 D. 11和12之间
7.实数a 在数轴上的位置如图所示,则 化简后为( ).
A. 7 B. - 7 C. 2a-15 D.无法确定
8.已知 且a>b>0,则 的值是( ).
A. B. C. D.
第Ⅱ卷(非选择题 共84分)
二、填空题(每题3分,共30分)
9.(2024·南京玄武区二模)若式子 在实数范围内有意义,则x的取值范围是 .
10.请写出一个正整数m的值使得 m是整数:m=
11.(2024·扬州仪征一模)已知实数a 满足条件 那么a-2023 的值为 .
12. 用“<”把下列各数连接起来:—3 、3.14、π、-0.13、——2 : .
13. 已知xy<0,化简:
14. 如果 那么a 的取值范围是 .
15.已知三角形三边分别为 则它的周长为 cm.
16. (2024·连云港连云区模拟)若 则a的值为 .
17. 若x、y为实数,且| 则 的值为 .
18. 已知 当x分别取1、2、3、…、2024时,所对应y值的总和是 .
三、解答题(第19~22题每题6分,第23、24题每题7分,第25、26题每题8分,共54分)
19. 计算:
(1)(2024·镇江丹徒区期末)
(2)(2024·常州溧阳期末)
20. 化简
21. 如图,在平面直角坐标系中,点A、B 的坐标分别为A(a,0)、B(b,0),且a、b满足 点C的坐标为(0,3).
(1)求a、b的值及
(2)若点M在x轴上,且 试求点 M 的坐标.
22.先阅读下列材料,再解决问题:
阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去一层根号.例如:
解决问题:
(1)模仿上例的过程填空:
(2)根据上述思路,试将下列二次根式化简
23.(2024·宿迁宿城区期末)[再读教材]我们八年级下册数学课本第161页介绍了“海伦——秦九韶公式”:如果一个三角形的三边长分别为a、b、c,记 那么三角形的面积为
[解决问题]如图,在 中,
(1)请你用“海伦一秦九韶公式”求 的面积.
(2)除了利用“海伦—秦九韶公式”求 的面积外,你还有其他的解法吗 请写出你的解法.
24. 像( ·两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.
(1)请写出以下代数式的一个有理化因式:
(2)化简
(3)当 时,直接写出代数式 的最大值: .
25.(2024·甘肃武威凉州区期末)如图,小明家有一块长方形空地ABCD,长BC为 宽AB为 ,现要在空地中挖一个长方形的水池(即图中阴影部分),其余部分种植草莓.其中长方形水池的长为 宽为
(1)求长方形空地ABCD的周长.(结果化为最简二次根式)
(2)已知小明家种植的草莓售价为8元/千克,且每平方米产草莓15千克,若小明家将所种的草莓全部销售完,销售收入为多少元
26.(2024·南通通州区育才中学月考)规定:关于x、y的二元一次方程 有无数组解,每组解记为P(x,y),称点P(x,y)为“坐标点”,将这些“坐标点”连接新得到一条直线,称这条直线是“坐标点”的“关联线”,回答下列问题:
(1)已知 ),则是“关联线 的“坐标点”的是 ;
(2)若A(1,1)、B(4,-1)是“关联线 的“坐标点”,求a、b的值;
(3)已如m、n 是实数,且 若 是“关联线 的一个“坐标点”,用等式表示s 与m之间的关系,并求出s 的最小值.
1. A
2. D [解析] 与 不是同类二次根式,故A 不符合题意;] 与 不是同类二次根式,故B不符合题意;C. 不是同类二次根式,故C不符合题意;I 与 是同类二次根式,故D符合题意.故选D.
3. D [解析] 不是同类二次根式,不能合并,此选项不合题意; 此选项不合题意; 此选项不合题意; 此选项符合题意.故选 D.
4. C [解析]由题意,得另一条直角边的长为 故选C.
5. B
6. C [解析] 而 故选C.
7. A [解析]由数轴,得5
8. D [解析]∵
即
同理可得
故选 D.
9. x≤5 [解析]由题意,得5-x≥0,解得x≤5.
10.2(答案不唯一)
11.2024 [解析].
∴a-2024≥0,即a≥2024,∴2023-a<0,
[解析]∵二次根式 有意义,∴y<0.∵xy<0,∴x>0.
14.-3
17.1
18.16186 [解析]由题意,得.y=x+5--|x-3|,当x≤3时,y=x+5+x-3=2x+2,当x>3时,y=x+5-(x-3)=x+5-x+3=8,∴y值的总和为4+6+8+8+8+…+8=4+6+8×2022=16186.
19.(1)9 (2)-2
21.(1)∵a、b满足( ∴b=4,a=-1,∴A(-1,0)、B(4,0),
(2)设M 的坐标为(m,0),
∴当 时, 当 时,
∴符合条件的点M的坐标为(( ,0)和(
(2)原式
23.(1)∵三角形三边长分别为4、5、7,
(2)有其他的解法.解法如下:
过点C 作 CH⊥AB 于点 H,设 AH=x,则 BH=7-x,
在Rt△ACH 中,
在Rt△BCH 中,
解得
在Rt△ACH 中,
(答案不唯一)
(2)原式
[解析 ] ∴当 a =2 时, 有最小值,最小值为 此时 的值最大,最大值为
故代数式 的最大值为
方法诠释 要求 的最大值,是很困难的,但我们可以逆用分母有理化也就是分子有理化,可得 而 在自变量的取值范围内是可以求出它的最小值的.
25.(1)长方形空地ABCD的周长:
故长方形空地 ABCD 的周长为
(2)种草莓的面积为
39×15×8=4680(元).
故销售收入为4680元.
26.(1)P (-1,3) [解析]由于 P (--1,3)是二元一次方程x+y=2的解,而P (4,-1)、P (1,2)不是二元一次方程x+y=2的解,
∴“关联线” x+y=2的“坐标点”的是P (-1,3).
(2)∵A(1,1)、B(4,-1)是“关联线”(a+1)x+by=5的“坐标点”,
解得
∴a=1,b=3.
是“关联线’” 5x-2y=s的一个“坐标点”,
即s-3≥0,∴s≥3,
∴s的最小值为3.
故s 与m 之间的关系为 s的最小值是3.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
