第11章反比例函数提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 第11章反比例函数提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 04:56:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第11章反比例函数提优测评卷
时间:90分钟 总分:100分
第Ⅰ卷(选择题 共16分)
一、选择题(每题2分,共16分)
1. (2024·重庆中考)已知点(-3,2)在反比例函数 的图像上,则k 的值为( ).
A. - 3 B. 3 C. - 6 D. 6
2.下列函数中,y是x的反比例函数的是( ).
D. x(y-1)=1
3.(2023·湘潭中考)如图,在平面直角坐标系中,O是坐标原点,点A 是反比例函数 图像上的一点,过点A 分别作AM⊥x轴于点M,AN⊥y轴于点N,若四边形AMON 的面积为2,则k 的值是( ).
A. 2 B. - 2 C. 1 D. - 1
4.(2024·天津中考)若点 A(x ,-1)、B(x ,1)、C(x ,5)都在反比例函数 的图像上,则x 、x 、x 的大小关系是( ).
5.(2023·绥化中考)如图,在平面直角坐标系中,点A 在y轴的正半轴上,AC平行于x轴,点B、C的横坐标都是3,BC=2,点D在AC上,且其横坐标为1,若反比例函数. 的图像经过点 B、D,则k 的值是( ).
A. 1 B. 2 C. 3 D.
6.(2024·黑龙江中考)如图,双曲线 经过A、B 两点,连接OA、AB,过点 B 作BD⊥y轴,垂足为D,BD交OA 于点E,且E 为AO的中点,则△AEB 的面积是( ).
A. 4.5 B. 3.5 C. 3 D. 2.5
7.如果 100 N 的压力 F 作用于物体上,产生的压强p 要大于1000 Pa,则下列关于物体受力面积S(m )的说法正确的是( ).
A. S小于0.1m B. S大于0.1m C. S小于10m D. S大于10m
8.学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图像上,则成绩优秀人数最多的是( ).
A. 八(1)班 B. 八(2)班 C. 八(3)班 D. 八(4)班
第Ⅱ卷(非选择题 共84分)
二、填空题(每题3分,共30分)
9. (2024·扬州江都区一模)若函数 与y=-2x-4的图像的交点坐标为(a,b),则 的值是
10.跨学科 欧姆定律(2023·广东中考)某蓄电池的电压为48 V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为 当R=12Ω时,I的值为 A.
11.(2024·南京鼓楼区二模)在平面直角坐标系中,直线y=kx(k≠0)与双曲线 交于A(x ,y )、B(x ,y )两点,则 的值为 .
12.已知函数 当x<0时,y随x的增大而减小,则k的取值范围是 .
13.如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A 在反比例函数 的图像上,则菱形的面积为 .
14.点 P 为函数 图像上一点,若P 到原点的距离为2,则符合条件的点 P 有 个.
15.如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数 的图像交于A、B 两点,则四边形 MAOB 的面积为 .
16.(2024·齐齐哈尔中考)如图,反比例函数 的图像经过平行四边形ABCO 的顶点A,OC在x轴上,若点B(-1,3),S ABCO=3,则实数k 的值为 .
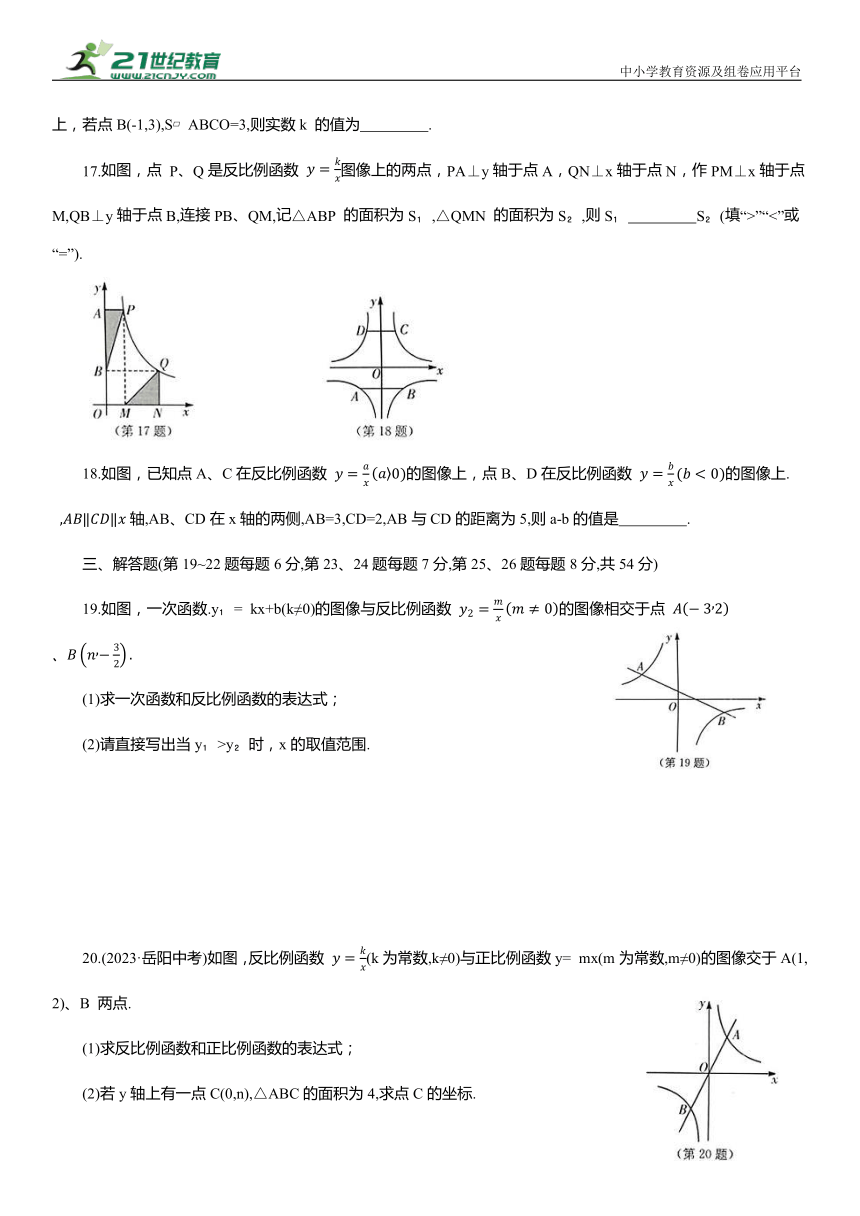
17.如图,点 P、Q是反比例函数 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记△ABP 的面积为S ,△QMN 的面积为S ,则S S (填“>”“<”或“=”).
18.如图,已知点A、C在反比例函数 的图像上,点B、D在反比例函数 的图像上. 轴,AB、CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是 .
三、解答题(第19~22题每题6分,第23、24题每题7分,第25、26题每题8分,共54分)
19.如图,一次函数.y = kx+b(k≠0)的图像与反比例函数 的图像相交于点
(1)求一次函数和反比例函数的表达式;
(2)请直接写出当y >y 时,x的取值范围.
20.(2023·岳阳中考)如图,反比例函数 (k为常数,k≠0)与正比例函数y= mx(m为常数,m≠0)的图像交于A(1,2)、B 两点.
(1)求反比例函数和正比例函数的表达式;
(2)若y轴上有一点C(0,n),△ABC的面积为4,求点C的坐标.
21.蓄电池的电压为定值,使用此电源时,电流I(A)和电阻R(Ω)成反比例函数关系,且当 时,
(1)蓄电池的电压是多少 请你写出函数的表达式.
(2)当电流为5 A时,电阻是多少
(3)当电阻是10Ω时,电流是多少
(4)如果以此蓄电池为电源的用电器限制电流不超过10 A,那么用电器的可变电阻应该控制在什么范围内
22. (2024·广安中考)如图,一次函数 (a、b为常数, 的图像与反比例函数 (k为常数, 的图像交于A(2,4)、B(n,-2)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB与x轴交于点C,点P(m,0)是x轴上的点,若 的面积大于12,请直接写出m 的取值范围.
23.抗体浓度某制药公司生产3支单针疫苗和2支双针疫苗需要19 min,生产2支单针疫苗和1支双针疫苗需要1 1 min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/mL)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度y首先与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/mL时,并且不低于23 min/mL,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗 请通过计算说明.
24.(2024·甘肃中考)如图,在平面直角坐标系中,将函数y=ax 的图像向上平移3个单位长度,得到一次函数y=ax+b的图像,与反比例函数 的图像交于点A(2,4).过点B(0,2)作x轴的平行线分别交y=ax+b与 的图像于 C、D两点.
(1)求一次函数y=ax+b和反比例函数 的表达式;
(2)连接AD,求△ACD的面积.
25.如图,在平面直角坐标系中,菱形ABCD的顶点D在y轴上,A、C两点的坐标分别为(4,0)、(4,m),直线CD: 与反比例函数 的图像交于C、 两点.
(1)求该反比例函数的表达式及m 的值;
(2)判断点 B 是否在该反比例函数的图像上,并说明理由.
26. (2024·遂宁中考)如图,一次函数 的图像与反比例函数 的图像相交于A(1,3)、B(n,-1)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图像,直接写出 时,x的取值范围;
(3)过点B 作直线OB,交反比例函数图像于点C,连接AC,求 的面积.
1. C [解析]由题意,得k=-3×2=-6.故选C.
2. C [解析 是正比例函数,不是反比例函数,故此选项不合题意;
B.不是反比例函数,故此选项不符合题意;
C.是反比例函数,故此选项符合题意;
D.不是反比例函数,故此选项不符合题意.故选 C.
3. A [解析]由题意,设A(a,b),∴ab=k.
又S四边形ANOM=2= ab,∴k=2.故选 A.
4. B [解析]∵k=5>0,∴反比例函数 的图像分布在第一、三象限,在每个象限内,y随x的增大而减小.∵点A(x ,-1)、B(x ,1)、C(x ,5)都在反比例函数 的图像上,∴点A(x ,-1)分布在第三象限,B(x ,1)、C(x ,5)分布在第一象限,且 故选 B.
5. C [解析]由题意设B(3,a),则D(1,a+2).
∵反比例函数 的图像经过点 B、D,∴3a=a+2,解得a=1,∴B(3,1),∴k=3×1=3.故选C.
6. A [解析]过点 A 作AM⊥y轴,垂足为 M,连接OB,则
∵E 是OA 的中点,即OE=AE,而DE∥AM,
即
故选 A.
7. A [解析]
∵产生的压强p 要大于1000 Pa,
故选 A.
8. A [解析]由题意,得xy的值即为班级成绩优秀人数.∵描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图像上,
∴八(2)、八(4)两个班级的优秀人数相同.
∵八(1)点在反比例图像上方,八(3)点在反比例函数图像下方,
∴八(1)班的 xy的值最大,八(3)班的 xy的值最小,即八(1)班优秀人数>八(2)班优秀人数=八(4)班优秀人数>八(3)班优秀人数,
∴八(1)班的优秀人数最多.故选 A.
9.-2 [解析]∵函数 与.y=-2x-4的图像的交点坐标为(a,b),∴b= ,b=-2a-4,∴ab=2,
10.4 [解析]当R=12Ω时,
11.-12 [解析]∵点A(x ,y )、B(x ,y )是双曲线 上的点,
∵直线y= kx(k≠0)与双曲线 交于A(x ,y )、B(x ,y )两点,
关于原点对称,
∴原式=
[解析]∵当x<0时,y随x的增大而减小,
13.4 [解析]如图,连接AC交OB 于D.
∵四边形OABC是菱形,∴AC⊥OB.
∵点A 在反比例函数. 的图像上,
14.2
15.10 [解析]由图可得
16.—6 [解析]如图,延长AB交y轴于点D.
∵B(-1,3),S□ABco=3,∴OC·OD=3OC=3.
∵四边形ABCO是平行四边形,∴AB=OC=1,
∴AD=2,∴A(-2,3).
∵点A 在反比例函数图像上,∴k=-6.
17.= 18.6
19.(1)∵反比例函数 的图像经过点A(-3,2),∴m=-3×2=-6.
∴反比例函数的表达式为
在反比例函数 图像上,
∴n=4,∴点B 的坐标为
∵一次函数. 的图像经过点A(-3,
2)和点
解得
∴一次函数的表达式为
(2)观察图像,y >y 时,x的取值范围是x<-3或020.(1)将A(1,2)代入 得k=2,∴反比例函数的表达式为 将A(1,2)代入y= mx,得m=2,
∴正比例函数的表达式为y=2x.
(2)解方程组 得
∴点 B 的坐标为(-1,-2).
如图,过点 A、B分别作y 轴的垂线,垂足分别为E、F.
∵A(1,2)、B(-1,-2)、C(0,n),
∴AE=BF=1,OC=|n|.
即|n|×1+|n|×1=8,∴|n|=4,
∴n=±4,∴点C的坐标为(0,4)或(0,-4).
21.(1)U=IR=4×5=20(V),函数表达式是
(2)当I=5A时,R=4Ω.
(3)当R=10Ω时,I=2A.
(4)因为电流不超过10A,
由 可得 解得R≥2,
故可变电阻应该大于或等于2Ω.
22.(1)把点A(2,4)代入 得k=8,
∴反比例函数的表达式为
把点B(n,-2)代入 得n=-4.
∵点A(2,4)、B(-4,-2)在一次函数y= ax+b的图像上,
解得
∴一次函数的表达式为y=x+2.
(2)在函数y=x+2中,当y=0时,x=-2,∴C(-2,0),
设点 P 坐标为(m,0),则PC=|m+2|.
解得m>4或m<-8.
23.(1)设生产1支单针疫苗需要a min,生产1支双针疫苗需要b min.
根据题意,得 解得
故生产1支单针疫苗需要3min,生产1支双针疫苗需要5min.
(2)当x>0.7时,设函数表达式为
将(0.7,910)代入,解得m=637,故
当y=50时,
当y=23时,
所以小明应在打第二针疫苗的时间段为打第一针后的第13天到27天内.
24.(1)∵函数y= ax+b的图像由函数y= ax 的图像向上平移3个单位长度得到,∴b=3.
将点A 坐标代入一次函数表达式,得2a+3=4,解得 ∴一次函数表达式为
将点 A 坐标代入反比例函数表达式,得k=2×4=8,
∴反比例函数表达式为
(2)将y=2代入 得 解得x=-2,∴点C的坐标为(-2,2).
将y=2代入 得x=4,∴点D的坐标为(4,2),∴CD=4-(-2)=6,
25.(1)把点 P(-8,-2)代入 得 解得k=16.∴反比例函数的表达式为 ∵点C(4,m)在反比例函数 的图像上,
(2)点B 在反比例函数的图像上.理由如下:如图,连接AC、BD 交于点H.
把点C(4,4)、P(-8,-2)代入y= ax+b,
得 解得
∴直线CD的函数表达式是
在 中,令x=0得y=2,∴D(0,2).
∵四边形 ABCD 是菱形,∴点 H 是AC、BD 中点.
由点A(4,0)、C(4,4)可得点 H(4,2),
设B(p,q).∵D(0,2),
解得
在 中,令x=8,得y=2,
∴点 B 在反比例函数 的图像上.
26.(1)将点A 坐标代入反比例函数表达式,得m=1×3=3,∴反比例函数表达式为
将点 B 坐标代入反比例函数表达式,得n=-3,∴点 B 的坐标为(-3,-1).
将A、B两点坐标代入一次函数表达式,
得 解得
∴一次函数表达式为
(2)由函数图像可知,当-31时,一次函数的图像在反比例函数图像的上方,即y >y ,∴当.y >y 时,x的取值范围为-31.
(3)如图,连接AO,令直线AB与x轴的交点为M.
将y=0代入y=x+2,得x=-2,∴点M的坐标为(-2,0),
1=4.
∵正比例函数图像与反比例函数图像都是中心对称图形,且坐标原点是对称中心,
∴点B 和点C关于点O成中心对称,∴BO=CO,∴S△ABC=2S△AOB=8.
第11章反比例函数提优测评卷
时间:90分钟 总分:100分
第Ⅰ卷(选择题 共16分)
一、选择题(每题2分,共16分)
1. (2024·重庆中考)已知点(-3,2)在反比例函数 的图像上,则k 的值为( ).
A. - 3 B. 3 C. - 6 D. 6
2.下列函数中,y是x的反比例函数的是( ).
D. x(y-1)=1
3.(2023·湘潭中考)如图,在平面直角坐标系中,O是坐标原点,点A 是反比例函数 图像上的一点,过点A 分别作AM⊥x轴于点M,AN⊥y轴于点N,若四边形AMON 的面积为2,则k 的值是( ).
A. 2 B. - 2 C. 1 D. - 1
4.(2024·天津中考)若点 A(x ,-1)、B(x ,1)、C(x ,5)都在反比例函数 的图像上,则x 、x 、x 的大小关系是( ).
5.(2023·绥化中考)如图,在平面直角坐标系中,点A 在y轴的正半轴上,AC平行于x轴,点B、C的横坐标都是3,BC=2,点D在AC上,且其横坐标为1,若反比例函数. 的图像经过点 B、D,则k 的值是( ).
A. 1 B. 2 C. 3 D.
6.(2024·黑龙江中考)如图,双曲线 经过A、B 两点,连接OA、AB,过点 B 作BD⊥y轴,垂足为D,BD交OA 于点E,且E 为AO的中点,则△AEB 的面积是( ).
A. 4.5 B. 3.5 C. 3 D. 2.5
7.如果 100 N 的压力 F 作用于物体上,产生的压强p 要大于1000 Pa,则下列关于物体受力面积S(m )的说法正确的是( ).
A. S小于0.1m B. S大于0.1m C. S小于10m D. S大于10m
8.学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图像上,则成绩优秀人数最多的是( ).
A. 八(1)班 B. 八(2)班 C. 八(3)班 D. 八(4)班
第Ⅱ卷(非选择题 共84分)
二、填空题(每题3分,共30分)
9. (2024·扬州江都区一模)若函数 与y=-2x-4的图像的交点坐标为(a,b),则 的值是
10.跨学科 欧姆定律(2023·广东中考)某蓄电池的电压为48 V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为 当R=12Ω时,I的值为 A.
11.(2024·南京鼓楼区二模)在平面直角坐标系中,直线y=kx(k≠0)与双曲线 交于A(x ,y )、B(x ,y )两点,则 的值为 .
12.已知函数 当x<0时,y随x的增大而减小,则k的取值范围是 .
13.如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A 在反比例函数 的图像上,则菱形的面积为 .
14.点 P 为函数 图像上一点,若P 到原点的距离为2,则符合条件的点 P 有 个.
15.如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数 的图像交于A、B 两点,则四边形 MAOB 的面积为 .
16.(2024·齐齐哈尔中考)如图,反比例函数 的图像经过平行四边形ABCO 的顶点A,OC在x轴上,若点B(-1,3),S ABCO=3,则实数k 的值为 .
17.如图,点 P、Q是反比例函数 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记△ABP 的面积为S ,△QMN 的面积为S ,则S S (填“>”“<”或“=”).
18.如图,已知点A、C在反比例函数 的图像上,点B、D在反比例函数 的图像上. 轴,AB、CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是 .
三、解答题(第19~22题每题6分,第23、24题每题7分,第25、26题每题8分,共54分)
19.如图,一次函数.y = kx+b(k≠0)的图像与反比例函数 的图像相交于点
(1)求一次函数和反比例函数的表达式;
(2)请直接写出当y >y 时,x的取值范围.
20.(2023·岳阳中考)如图,反比例函数 (k为常数,k≠0)与正比例函数y= mx(m为常数,m≠0)的图像交于A(1,2)、B 两点.
(1)求反比例函数和正比例函数的表达式;
(2)若y轴上有一点C(0,n),△ABC的面积为4,求点C的坐标.
21.蓄电池的电压为定值,使用此电源时,电流I(A)和电阻R(Ω)成反比例函数关系,且当 时,
(1)蓄电池的电压是多少 请你写出函数的表达式.
(2)当电流为5 A时,电阻是多少
(3)当电阻是10Ω时,电流是多少
(4)如果以此蓄电池为电源的用电器限制电流不超过10 A,那么用电器的可变电阻应该控制在什么范围内
22. (2024·广安中考)如图,一次函数 (a、b为常数, 的图像与反比例函数 (k为常数, 的图像交于A(2,4)、B(n,-2)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB与x轴交于点C,点P(m,0)是x轴上的点,若 的面积大于12,请直接写出m 的取值范围.
23.抗体浓度某制药公司生产3支单针疫苗和2支双针疫苗需要19 min,生产2支单针疫苗和1支双针疫苗需要1 1 min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/mL)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度y首先与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/mL时,并且不低于23 min/mL,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗 请通过计算说明.
24.(2024·甘肃中考)如图,在平面直角坐标系中,将函数y=ax 的图像向上平移3个单位长度,得到一次函数y=ax+b的图像,与反比例函数 的图像交于点A(2,4).过点B(0,2)作x轴的平行线分别交y=ax+b与 的图像于 C、D两点.
(1)求一次函数y=ax+b和反比例函数 的表达式;
(2)连接AD,求△ACD的面积.
25.如图,在平面直角坐标系中,菱形ABCD的顶点D在y轴上,A、C两点的坐标分别为(4,0)、(4,m),直线CD: 与反比例函数 的图像交于C、 两点.
(1)求该反比例函数的表达式及m 的值;
(2)判断点 B 是否在该反比例函数的图像上,并说明理由.
26. (2024·遂宁中考)如图,一次函数 的图像与反比例函数 的图像相交于A(1,3)、B(n,-1)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图像,直接写出 时,x的取值范围;
(3)过点B 作直线OB,交反比例函数图像于点C,连接AC,求 的面积.
1. C [解析]由题意,得k=-3×2=-6.故选C.
2. C [解析 是正比例函数,不是反比例函数,故此选项不合题意;
B.不是反比例函数,故此选项不符合题意;
C.是反比例函数,故此选项符合题意;
D.不是反比例函数,故此选项不符合题意.故选 C.
3. A [解析]由题意,设A(a,b),∴ab=k.
又S四边形ANOM=2= ab,∴k=2.故选 A.
4. B [解析]∵k=5>0,∴反比例函数 的图像分布在第一、三象限,在每个象限内,y随x的增大而减小.∵点A(x ,-1)、B(x ,1)、C(x ,5)都在反比例函数 的图像上,∴点A(x ,-1)分布在第三象限,B(x ,1)、C(x ,5)分布在第一象限,且 故选 B.
5. C [解析]由题意设B(3,a),则D(1,a+2).
∵反比例函数 的图像经过点 B、D,∴3a=a+2,解得a=1,∴B(3,1),∴k=3×1=3.故选C.
6. A [解析]过点 A 作AM⊥y轴,垂足为 M,连接OB,则
∵E 是OA 的中点,即OE=AE,而DE∥AM,
即
故选 A.
7. A [解析]
∵产生的压强p 要大于1000 Pa,
故选 A.
8. A [解析]由题意,得xy的值即为班级成绩优秀人数.∵描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图像上,
∴八(2)、八(4)两个班级的优秀人数相同.
∵八(1)点在反比例图像上方,八(3)点在反比例函数图像下方,
∴八(1)班的 xy的值最大,八(3)班的 xy的值最小,即八(1)班优秀人数>八(2)班优秀人数=八(4)班优秀人数>八(3)班优秀人数,
∴八(1)班的优秀人数最多.故选 A.
9.-2 [解析]∵函数 与.y=-2x-4的图像的交点坐标为(a,b),∴b= ,b=-2a-4,∴ab=2,
10.4 [解析]当R=12Ω时,
11.-12 [解析]∵点A(x ,y )、B(x ,y )是双曲线 上的点,
∵直线y= kx(k≠0)与双曲线 交于A(x ,y )、B(x ,y )两点,
关于原点对称,
∴原式=
[解析]∵当x<0时,y随x的增大而减小,
13.4 [解析]如图,连接AC交OB 于D.
∵四边形OABC是菱形,∴AC⊥OB.
∵点A 在反比例函数. 的图像上,
14.2
15.10 [解析]由图可得
16.—6 [解析]如图,延长AB交y轴于点D.
∵B(-1,3),S□ABco=3,∴OC·OD=3OC=3.
∵四边形ABCO是平行四边形,∴AB=OC=1,
∴AD=2,∴A(-2,3).
∵点A 在反比例函数图像上,∴k=-6.
17.= 18.6
19.(1)∵反比例函数 的图像经过点A(-3,2),∴m=-3×2=-6.
∴反比例函数的表达式为
在反比例函数 图像上,
∴n=4,∴点B 的坐标为
∵一次函数. 的图像经过点A(-3,
2)和点
解得
∴一次函数的表达式为
(2)观察图像,y >y 时,x的取值范围是x<-3或0
∴正比例函数的表达式为y=2x.
(2)解方程组 得
∴点 B 的坐标为(-1,-2).
如图,过点 A、B分别作y 轴的垂线,垂足分别为E、F.
∵A(1,2)、B(-1,-2)、C(0,n),
∴AE=BF=1,OC=|n|.
即|n|×1+|n|×1=8,∴|n|=4,
∴n=±4,∴点C的坐标为(0,4)或(0,-4).
21.(1)U=IR=4×5=20(V),函数表达式是
(2)当I=5A时,R=4Ω.
(3)当R=10Ω时,I=2A.
(4)因为电流不超过10A,
由 可得 解得R≥2,
故可变电阻应该大于或等于2Ω.
22.(1)把点A(2,4)代入 得k=8,
∴反比例函数的表达式为
把点B(n,-2)代入 得n=-4.
∵点A(2,4)、B(-4,-2)在一次函数y= ax+b的图像上,
解得
∴一次函数的表达式为y=x+2.
(2)在函数y=x+2中,当y=0时,x=-2,∴C(-2,0),
设点 P 坐标为(m,0),则PC=|m+2|.
解得m>4或m<-8.
23.(1)设生产1支单针疫苗需要a min,生产1支双针疫苗需要b min.
根据题意,得 解得
故生产1支单针疫苗需要3min,生产1支双针疫苗需要5min.
(2)当x>0.7时,设函数表达式为
将(0.7,910)代入,解得m=637,故
当y=50时,
当y=23时,
所以小明应在打第二针疫苗的时间段为打第一针后的第13天到27天内.
24.(1)∵函数y= ax+b的图像由函数y= ax 的图像向上平移3个单位长度得到,∴b=3.
将点A 坐标代入一次函数表达式,得2a+3=4,解得 ∴一次函数表达式为
将点 A 坐标代入反比例函数表达式,得k=2×4=8,
∴反比例函数表达式为
(2)将y=2代入 得 解得x=-2,∴点C的坐标为(-2,2).
将y=2代入 得x=4,∴点D的坐标为(4,2),∴CD=4-(-2)=6,
25.(1)把点 P(-8,-2)代入 得 解得k=16.∴反比例函数的表达式为 ∵点C(4,m)在反比例函数 的图像上,
(2)点B 在反比例函数的图像上.理由如下:如图,连接AC、BD 交于点H.
把点C(4,4)、P(-8,-2)代入y= ax+b,
得 解得
∴直线CD的函数表达式是
在 中,令x=0得y=2,∴D(0,2).
∵四边形 ABCD 是菱形,∴点 H 是AC、BD 中点.
由点A(4,0)、C(4,4)可得点 H(4,2),
设B(p,q).∵D(0,2),
解得
在 中,令x=8,得y=2,
∴点 B 在反比例函数 的图像上.
26.(1)将点A 坐标代入反比例函数表达式,得m=1×3=3,∴反比例函数表达式为
将点 B 坐标代入反比例函数表达式,得n=-3,∴点 B 的坐标为(-3,-1).
将A、B两点坐标代入一次函数表达式,
得 解得
∴一次函数表达式为
(2)由函数图像可知,当-3
(3)如图,连接AO,令直线AB与x轴的交点为M.
将y=0代入y=x+2,得x=-2,∴点M的坐标为(-2,0),
1=4.
∵正比例函数图像与反比例函数图像都是中心对称图形,且坐标原点是对称中心,
∴点B 和点C关于点O成中心对称,∴BO=CO,∴S△ABC=2S△AOB=8.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
