第8章认识概率提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 第8章认识概率提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 05:13:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第8章认识概率提优测评卷
时间:90分钟 总分:100分
第Ⅰ卷(选择题 共16分)
一、选择题(每题2分,共16分)
1.成语是中国文化的瑰宝,下列成语描述的事件是不可能事件的是( ).
A.守株待兔 B.水中捞月 C.旭日东升 D.水涨船高
2.不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( ).
A.摸出的是3个白球 B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球 D.摸出的是2个黑球、1个白球
3.(2024·淮安模拟)数轴上表示a、b两数的点分别在原点左、右两侧,下列事件是随机事件的是( ).
A. a+b>0 B. a-b>0 C. a·b>0 D. a÷b<0
4.在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色…如此大量的摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定于30%;②若从布袋中随机摸出一球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是( ).
A. ①②③ B. ①② C. ①③ D. ②③
5.下列说法正确的是( ).
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为
C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D.“抛一枚正方体骰子,朝上的点数为2的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 附近
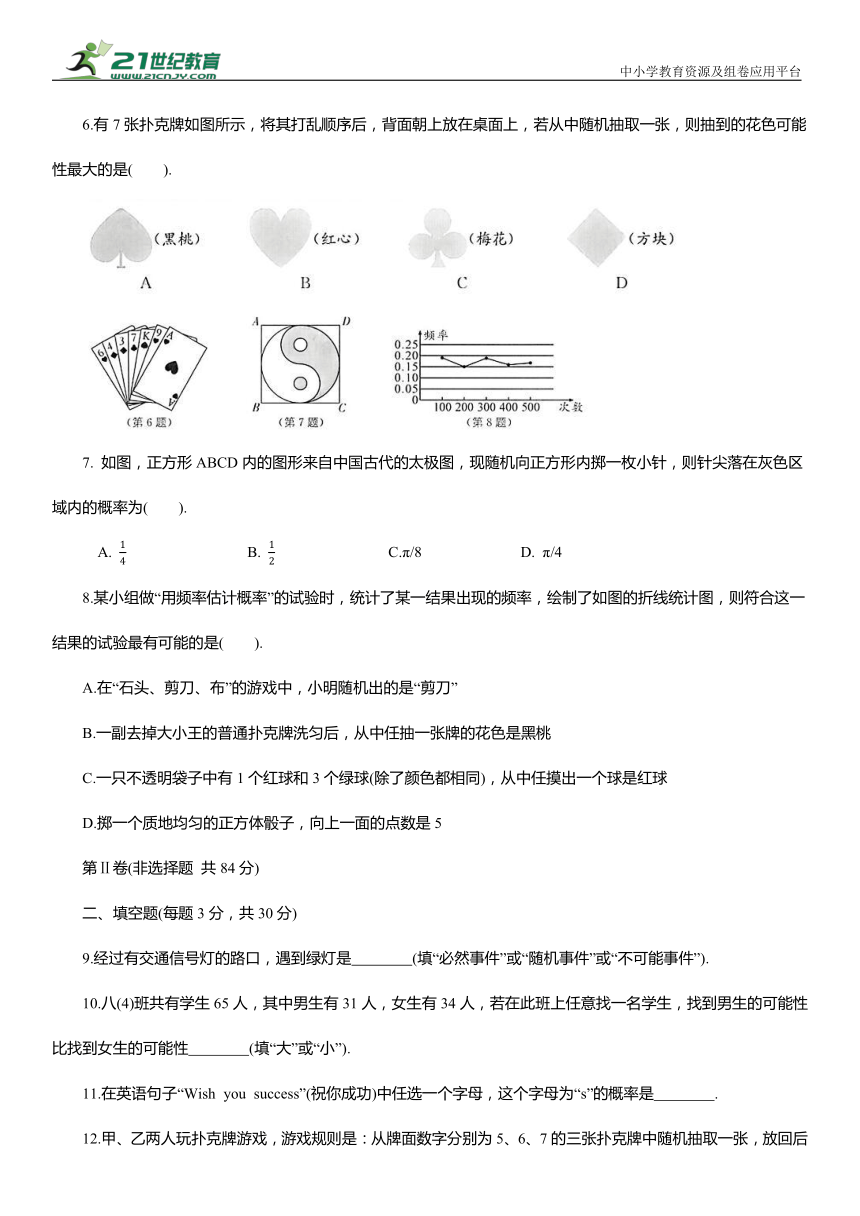
6.有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上,若从中随机抽取一张,则抽到的花色可能性最大的是( ).
7. 如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在灰色区域内的概率为( ).
A. B. C.π/8 D. π/4
8.某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( ).
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是黑桃
C.一只不透明袋子中有1个红球和3个绿球(除了颜色都相同),从中任摸出一个球是红球
D.掷一个质地均匀的正方体骰子,向上一面的点数是5
第Ⅱ卷(非选择题 共84分)
二、填空题(每题3分,共30分)
9.经过有交通信号灯的路口,遇到绿灯是 (填“必然事件”或“随机事件”或“不可能事件”).
10.八(4)班共有学生65人,其中男生有31人,女生有34人,若在此班上任意找一名学生,找到男生的可能性比找到女生的可能性 (填“大”或“小”).
11.在英语句子“Wish you success”(祝你成功)中任选一个字母,这个字母为“s”的概率是 .
12.甲、乙两人玩扑克牌游戏,游戏规则是:从牌面数字分别为5、6、7的三张扑克牌中随机抽取一张,放回后再随机抽取一张,若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽取的两张牌面数字的积为偶数,则乙获胜.这个游戏 (填“公平”或“不公平”).
13.传统文化 谚语(2024·湖南长沙一模)“八月十五云遮月,正月十五雪打灯”是一句谚语,意思是说如果八月十五晚上阴天的话,正月十五晚上就下雪,你认为这个谚语说的是 .(填写“必然事件”或“不可能事件”或“随机事件”)
14.大数据分析技术在生活中有着重要作用.如图是小明同学的学生信息码示意图,用黑白打印机打印在边长为3cm的正方形区域内,为了估计图中白色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入白色部分的频率稳定在0.4左右,据此可以估计白色部分的总面积约为 cm .
15.箱子中有5个白球、7个黑球及m个红球.它们仅颜色不同,若从中随机摸出一球,结果是红球的可能性比黑球的可能性小,同时又比白球的可能性大,则m的值是
16.在一个不透明的口袋中有红色、黄色和绿色球共60个,它们除颜色外,其余完全相同.在不倒出球的情况下,要估计袋中各种颜色球的个数.同学们通过大量的摸球试验后,发现摸到红球和绿球的频率分别稳定在20%和40%.由此推测口袋中黄球的个数是 个.
17.一枚正方体骰子六个面上分别标有数字1、2、3、4、5、6,若连续抛掷四次,朝上一面的点数都为6,则第五次抛掷朝上一面的点数为6的概率为 .
18.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有 人.
三、解答题(第19~22题每题6分,第23、24题每题7分,第25、26题每题8分,共54分)
19.(2024·宿迁泗洪期中)在一个不透明的袋子中装有1个白球、2个黄球和3个红球,这些球除颜色外都相同,从中任意摸出一个球观察它的颜色.下列事件:①摸出的球是红色;②摸出的球是白色;③摸出的球是黄色;④摸出的球不是白色;⑤摸出的球不是黄色.估计各事件发生的可能性大小,回答下列问题:
(1)可能性最大和最小的事件分别是哪个(用序号表示)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列(用序号表示).
20.小强和小明两个同学设计一种同时抛出两枚1元硬币的游戏,游戏规则如下:如果抛出的硬币落下后朝上的两个面都为1元,则小强得1分,其余情况小明得1分,谁先得到10分谁就赢得比赛.你认为这个游戏规则公平吗 若不公平,怎样改正
21. 甲、乙两人玩一种游戏:共10张牌,牌面上分别写有-5、-4、-3、-2、-1、1、2、3、4、5,洗好牌后,将背面朝上,每人从中任意抽取三张,然后将牌面上的三个数相乘,结果较大者获胜.
(1)你认为抽取到哪三张牌时,不管对方抽取其他怎样的三张牌,你都会赢
(2)结果等于8的可能性有几种 把每一种都写出来.
22.李老师有一本2025年的日历簿,他任意翻了一下.
(1)翻出2月 30日是什么事件
(2)翻出偶数号和翻出奇数号的可能性哪个大
(3)翻出日期为3的倍数和日期为5的倍数的可能性哪个大
23.在一个不透明的盒子里装有黑、白两种颜色的球,这些球除颜色外都相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的部分统计数据:
摸球的 次数n 10 20 50 100 200 400 500 1000 2 000
摸到白球的次数m 4 7 10 28 45 97 127 252 498
摸到白球 的频率m 0.400 0.350 0.200 0.280 0.225 0.243 0.254 0.252 0.249
(1)摸到白球的概率的估计值是多少 请说明理由.(精确到0.01)
(2)某小组进行“用频率估计概率”的试验,符合(1)中结果的试验最有可能的是 .(填序号).
①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上;
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲;
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时,面朝上点数“小于3”.
24.(2024·益阳二模)“校园手机”现象越来越受到社会的关注.九(1)班学生在“统计实习”实践活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图.
(1)在图(2)中,AB 是⊙O的直径,求这次调查的家长总人数,并补全图(1).
(2)求图(2)中表示家长“基本赞成”的圆心角的度数.
(3)从这次接受调查的家长中,随机抽查一个,恰好是“无所谓”态度的家长的概率是多少
家长对“中学生带手机到学 家长对“中学生带手机到学
25.(2024·江西模拟)主题为“安全骑行,从头盔开始”的安全教育活动在某市全面开展.为了解市民骑电动自行车出行自觉佩戴头盔的情况,某数学实践探究小组在某路口进行调查,经过连续6天的同一时段的调查统计,得到数据并整理如下表:
经过路口的电动自行车数量/辆 180 230 300 260 240 280
自觉佩戴头盔人数/人 171 216 285 250 228 266
自觉佩戴头盔的频率 0.95 0.94 0.95 0.96 0.95 m
(1)表格中
(2)由此数据可估计,经过该路口的电动自行车骑行者佩戴了头盔的概率为 .(结果精确到0.01)
(3)若该小组某天调查到经过该路口的电动自行车共有1200辆,请问其中佩戴了头盔的骑行者大约有多少人
26.新情境转盘抽奖 如图,某商场有一个可以自由转动的圆形转盘.规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”的次数m 68 111 136 345 546 701
落在“铅笔”的频率m 0.68 0.74 0.68 0.69 0.68 0.70
(1)转动该转盘一次,获得一瓶饮料的概率约为 ;(结果精确到0.1)
(2)经统计该商场每天约有5 000名顾客参加抽奖活动,一瓶饮料和一支铅笔单价和为4元,支出的铅笔和饮料的奖品总费用是8000元,请计算该商场每支铅笔和每瓶饮料的费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在6000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
1. B
2. A [解析]∵从袋子中一次摸出3个球,而袋中一共只有2个白球,∴不可能摸出3个白球.故选 A.
3. A [解析]∵a、b两数的点分别在原点左、右两侧,∴a<0,b>0. A. a+b>0,是随机事件;B. a-b>0,是不可能事件;C. a·b>0,是不可能事件;D.a÷b<0,是必然事件.故选 A.
4. B [解析]摸出白球的频率为1--20%-50%=30%,故①正确;∵摸出黑球的频率稳定于 50%,∴摸出黑球的概率最大,故②正确;再摸100 次,摸出红球是随机事件,故③错误.故选 B.
5. D [解析]A.“明天下雨的概率为80%”指的是明天下雨的可能性是80%,故A错误;B.这是一个随机事件,抛一枚硬币,出现正面朝上或者反面朝上都有可能,但事先无法预料,故B错误;C.这是一个随机事件,买这种彩票,中奖或者不中奖都有可能,但事先无法预料,故C错误. D.正确.故选 D.
6. B[解析]∵抽到黑桃的概率为 ,抽到红心的概率为 ,抽到梅花的概率为 ,抽到方块的概率为 ∴抽到的花色可能性最大的是红心.故选 B.
7. C [解析]设正方形ABCD 的边长为2a,针尖落在黑色区域内的概率为故选 C.
8. D 9.随机事件
10.小 [解析]∵男生有31人,女生有34人,∴找到男生的可能性比找到女生的可能性小.
11. [解析]∵共有14个字母,其中“s”有4个,∴从中任选一个字母,这个字母为“s”的概率为
12.不公平 13.随机事件
14.3.6 [解析]∵经过大量重复试验,发现点落入白色部分的频率稳定在0.4左右,
∴估计点落入白色部分的概率为0.4.
∴估计白色部分的总面积为3×3×0.4=3.6(cm ).
15.6 [解析]∵箱子中有5个白球、7个黑球及m 个红球,从中随机摸出一球,结果是红球的可能性比黑球的可能性小,∴m<7.
∵同时又比白球的可能性大,∴5∴516.24 [解析]根据题意,得60×(1-20%-40%)=24(个),故推测口袋中黄球的个数是24个.
17. [解析]一枚正方体骰子六个面上分别标有数字1、2、3、4、5、6,若连续抛掷四次,朝上一面的点数都为6,则第五次抛掷朝上一面的点数为6的概率为
18.10
19.(1)由题意知,①摸出的球是红色的可能性大小为 ②摸出的球是白色的可能性大小为 ③摸出的球是黄色的可能性大小为- ④摸出的球不是白色的可能性大小为 ;⑤摸出的球不是黄色的可能性大小为 ,所以可能性最大的是④,最小的是②.
(2)②③①⑤④
20.这个游戏不公平.因为朝上的两个面都为1元的概率是 ,而其余情况的概率是 ,所以小强得分的概率是 ,而小明得分的概率是 ,所以不公平.可改为两面一样时,小强得1分,两面不一样时,小明得1分(答案不唯一).
21.(1)抽取到-5、-4、5,(-5)×(-4)×5=100最大.
(2)有4种,分别为 ①(-4)×(-2)×1=8;②(-4)×(-1)×2=8;③4×2×1=8;④(-2)×(-1)×4=8.
22.(1)翻出2月 30 日是不可能事件.
(2)翻出奇数号的可能性大.
(3)翻出日期为3的倍数的可能性大.
23.(1)摸到白球的概率的估计值是0.25.
理由:大量重复试验下,摸到白球的频率稳定在0.25附近,所以0.25 即概率的估计值.
(2)② [解析]①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上的概率是
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲的概率是
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时,面朝上点数“小于3”的概率是 故符合(1)中结果的试验最有可能的是②.
(1)由于AB 是⊙O的直径,所以“不赞成”占调查总人数的50%,所以总人数为200÷50%=400(人), “非常赞同”的人数为400×26%=104(人), “基本赞同”的人数为400-104-200-16=80(人).
补全的统计图如图.
家长对“中学生带手机到学校”态度的条形统计图
故题图(2)中表示家长“基本赞成”的圆心角的度数为72°.
(3)样本中,被调查的400名家长中,“无所谓”的有16名,所以随机抽查一个,恰好是“无所谓”态度的家长的概率是
故随机抽查一个,恰好是“无所谓”态度的家长的概率是
25.(1)0.95 (2)0.95
(3)1200×0.95=1140(人).
故佩戴了头盔的骑行者大约有1 140人.
26.(1)0.3 [解析]由表知,转动该转盘一次,获得铅笔的概率约为0.7,所以获得饮料的概率约为0.3.
(2)设该商场每支铅笔x元,每瓶饮料(4-x)元.
根据题意,得5000×(4-x)×0.3+5000x×0.7=8000,解得x=1,则4-x=4-1=3.
故该商场每支铅笔1元,每瓶饮料3元.
(3)36 [解析]设转盘上“一瓶饮料”区域的圆心角应调整为n度,则 解得n=36.
故转盘上“一瓶饮料”区域的圆心角应调整为36°.
第8章认识概率提优测评卷
时间:90分钟 总分:100分
第Ⅰ卷(选择题 共16分)
一、选择题(每题2分,共16分)
1.成语是中国文化的瑰宝,下列成语描述的事件是不可能事件的是( ).
A.守株待兔 B.水中捞月 C.旭日东升 D.水涨船高
2.不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( ).
A.摸出的是3个白球 B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球 D.摸出的是2个黑球、1个白球
3.(2024·淮安模拟)数轴上表示a、b两数的点分别在原点左、右两侧,下列事件是随机事件的是( ).
A. a+b>0 B. a-b>0 C. a·b>0 D. a÷b<0
4.在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色…如此大量的摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定于30%;②若从布袋中随机摸出一球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是( ).
A. ①②③ B. ①② C. ①③ D. ②③
5.下列说法正确的是( ).
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为
C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D.“抛一枚正方体骰子,朝上的点数为2的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 附近
6.有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上,若从中随机抽取一张,则抽到的花色可能性最大的是( ).
7. 如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在灰色区域内的概率为( ).
A. B. C.π/8 D. π/4
8.某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( ).
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是黑桃
C.一只不透明袋子中有1个红球和3个绿球(除了颜色都相同),从中任摸出一个球是红球
D.掷一个质地均匀的正方体骰子,向上一面的点数是5
第Ⅱ卷(非选择题 共84分)
二、填空题(每题3分,共30分)
9.经过有交通信号灯的路口,遇到绿灯是 (填“必然事件”或“随机事件”或“不可能事件”).
10.八(4)班共有学生65人,其中男生有31人,女生有34人,若在此班上任意找一名学生,找到男生的可能性比找到女生的可能性 (填“大”或“小”).
11.在英语句子“Wish you success”(祝你成功)中任选一个字母,这个字母为“s”的概率是 .
12.甲、乙两人玩扑克牌游戏,游戏规则是:从牌面数字分别为5、6、7的三张扑克牌中随机抽取一张,放回后再随机抽取一张,若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽取的两张牌面数字的积为偶数,则乙获胜.这个游戏 (填“公平”或“不公平”).
13.传统文化 谚语(2024·湖南长沙一模)“八月十五云遮月,正月十五雪打灯”是一句谚语,意思是说如果八月十五晚上阴天的话,正月十五晚上就下雪,你认为这个谚语说的是 .(填写“必然事件”或“不可能事件”或“随机事件”)
14.大数据分析技术在生活中有着重要作用.如图是小明同学的学生信息码示意图,用黑白打印机打印在边长为3cm的正方形区域内,为了估计图中白色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入白色部分的频率稳定在0.4左右,据此可以估计白色部分的总面积约为 cm .
15.箱子中有5个白球、7个黑球及m个红球.它们仅颜色不同,若从中随机摸出一球,结果是红球的可能性比黑球的可能性小,同时又比白球的可能性大,则m的值是
16.在一个不透明的口袋中有红色、黄色和绿色球共60个,它们除颜色外,其余完全相同.在不倒出球的情况下,要估计袋中各种颜色球的个数.同学们通过大量的摸球试验后,发现摸到红球和绿球的频率分别稳定在20%和40%.由此推测口袋中黄球的个数是 个.
17.一枚正方体骰子六个面上分别标有数字1、2、3、4、5、6,若连续抛掷四次,朝上一面的点数都为6,则第五次抛掷朝上一面的点数为6的概率为 .
18.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有 人.
三、解答题(第19~22题每题6分,第23、24题每题7分,第25、26题每题8分,共54分)
19.(2024·宿迁泗洪期中)在一个不透明的袋子中装有1个白球、2个黄球和3个红球,这些球除颜色外都相同,从中任意摸出一个球观察它的颜色.下列事件:①摸出的球是红色;②摸出的球是白色;③摸出的球是黄色;④摸出的球不是白色;⑤摸出的球不是黄色.估计各事件发生的可能性大小,回答下列问题:
(1)可能性最大和最小的事件分别是哪个(用序号表示)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列(用序号表示).
20.小强和小明两个同学设计一种同时抛出两枚1元硬币的游戏,游戏规则如下:如果抛出的硬币落下后朝上的两个面都为1元,则小强得1分,其余情况小明得1分,谁先得到10分谁就赢得比赛.你认为这个游戏规则公平吗 若不公平,怎样改正
21. 甲、乙两人玩一种游戏:共10张牌,牌面上分别写有-5、-4、-3、-2、-1、1、2、3、4、5,洗好牌后,将背面朝上,每人从中任意抽取三张,然后将牌面上的三个数相乘,结果较大者获胜.
(1)你认为抽取到哪三张牌时,不管对方抽取其他怎样的三张牌,你都会赢
(2)结果等于8的可能性有几种 把每一种都写出来.
22.李老师有一本2025年的日历簿,他任意翻了一下.
(1)翻出2月 30日是什么事件
(2)翻出偶数号和翻出奇数号的可能性哪个大
(3)翻出日期为3的倍数和日期为5的倍数的可能性哪个大
23.在一个不透明的盒子里装有黑、白两种颜色的球,这些球除颜色外都相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的部分统计数据:
摸球的 次数n 10 20 50 100 200 400 500 1000 2 000
摸到白球的次数m 4 7 10 28 45 97 127 252 498
摸到白球 的频率m 0.400 0.350 0.200 0.280 0.225 0.243 0.254 0.252 0.249
(1)摸到白球的概率的估计值是多少 请说明理由.(精确到0.01)
(2)某小组进行“用频率估计概率”的试验,符合(1)中结果的试验最有可能的是 .(填序号).
①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上;
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲;
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时,面朝上点数“小于3”.
24.(2024·益阳二模)“校园手机”现象越来越受到社会的关注.九(1)班学生在“统计实习”实践活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图.
(1)在图(2)中,AB 是⊙O的直径,求这次调查的家长总人数,并补全图(1).
(2)求图(2)中表示家长“基本赞成”的圆心角的度数.
(3)从这次接受调查的家长中,随机抽查一个,恰好是“无所谓”态度的家长的概率是多少
家长对“中学生带手机到学 家长对“中学生带手机到学
25.(2024·江西模拟)主题为“安全骑行,从头盔开始”的安全教育活动在某市全面开展.为了解市民骑电动自行车出行自觉佩戴头盔的情况,某数学实践探究小组在某路口进行调查,经过连续6天的同一时段的调查统计,得到数据并整理如下表:
经过路口的电动自行车数量/辆 180 230 300 260 240 280
自觉佩戴头盔人数/人 171 216 285 250 228 266
自觉佩戴头盔的频率 0.95 0.94 0.95 0.96 0.95 m
(1)表格中
(2)由此数据可估计,经过该路口的电动自行车骑行者佩戴了头盔的概率为 .(结果精确到0.01)
(3)若该小组某天调查到经过该路口的电动自行车共有1200辆,请问其中佩戴了头盔的骑行者大约有多少人
26.新情境转盘抽奖 如图,某商场有一个可以自由转动的圆形转盘.规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”的次数m 68 111 136 345 546 701
落在“铅笔”的频率m 0.68 0.74 0.68 0.69 0.68 0.70
(1)转动该转盘一次,获得一瓶饮料的概率约为 ;(结果精确到0.1)
(2)经统计该商场每天约有5 000名顾客参加抽奖活动,一瓶饮料和一支铅笔单价和为4元,支出的铅笔和饮料的奖品总费用是8000元,请计算该商场每支铅笔和每瓶饮料的费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在6000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
1. B
2. A [解析]∵从袋子中一次摸出3个球,而袋中一共只有2个白球,∴不可能摸出3个白球.故选 A.
3. A [解析]∵a、b两数的点分别在原点左、右两侧,∴a<0,b>0. A. a+b>0,是随机事件;B. a-b>0,是不可能事件;C. a·b>0,是不可能事件;D.a÷b<0,是必然事件.故选 A.
4. B [解析]摸出白球的频率为1--20%-50%=30%,故①正确;∵摸出黑球的频率稳定于 50%,∴摸出黑球的概率最大,故②正确;再摸100 次,摸出红球是随机事件,故③错误.故选 B.
5. D [解析]A.“明天下雨的概率为80%”指的是明天下雨的可能性是80%,故A错误;B.这是一个随机事件,抛一枚硬币,出现正面朝上或者反面朝上都有可能,但事先无法预料,故B错误;C.这是一个随机事件,买这种彩票,中奖或者不中奖都有可能,但事先无法预料,故C错误. D.正确.故选 D.
6. B[解析]∵抽到黑桃的概率为 ,抽到红心的概率为 ,抽到梅花的概率为 ,抽到方块的概率为 ∴抽到的花色可能性最大的是红心.故选 B.
7. C [解析]设正方形ABCD 的边长为2a,针尖落在黑色区域内的概率为故选 C.
8. D 9.随机事件
10.小 [解析]∵男生有31人,女生有34人,∴找到男生的可能性比找到女生的可能性小.
11. [解析]∵共有14个字母,其中“s”有4个,∴从中任选一个字母,这个字母为“s”的概率为
12.不公平 13.随机事件
14.3.6 [解析]∵经过大量重复试验,发现点落入白色部分的频率稳定在0.4左右,
∴估计点落入白色部分的概率为0.4.
∴估计白色部分的总面积为3×3×0.4=3.6(cm ).
15.6 [解析]∵箱子中有5个白球、7个黑球及m 个红球,从中随机摸出一球,结果是红球的可能性比黑球的可能性小,∴m<7.
∵同时又比白球的可能性大,∴5
17. [解析]一枚正方体骰子六个面上分别标有数字1、2、3、4、5、6,若连续抛掷四次,朝上一面的点数都为6,则第五次抛掷朝上一面的点数为6的概率为
18.10
19.(1)由题意知,①摸出的球是红色的可能性大小为 ②摸出的球是白色的可能性大小为 ③摸出的球是黄色的可能性大小为- ④摸出的球不是白色的可能性大小为 ;⑤摸出的球不是黄色的可能性大小为 ,所以可能性最大的是④,最小的是②.
(2)②③①⑤④
20.这个游戏不公平.因为朝上的两个面都为1元的概率是 ,而其余情况的概率是 ,所以小强得分的概率是 ,而小明得分的概率是 ,所以不公平.可改为两面一样时,小强得1分,两面不一样时,小明得1分(答案不唯一).
21.(1)抽取到-5、-4、5,(-5)×(-4)×5=100最大.
(2)有4种,分别为 ①(-4)×(-2)×1=8;②(-4)×(-1)×2=8;③4×2×1=8;④(-2)×(-1)×4=8.
22.(1)翻出2月 30 日是不可能事件.
(2)翻出奇数号的可能性大.
(3)翻出日期为3的倍数的可能性大.
23.(1)摸到白球的概率的估计值是0.25.
理由:大量重复试验下,摸到白球的频率稳定在0.25附近,所以0.25 即概率的估计值.
(2)② [解析]①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上的概率是
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众,正好抽到甲的概率是
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时,面朝上点数“小于3”的概率是 故符合(1)中结果的试验最有可能的是②.
(1)由于AB 是⊙O的直径,所以“不赞成”占调查总人数的50%,所以总人数为200÷50%=400(人), “非常赞同”的人数为400×26%=104(人), “基本赞同”的人数为400-104-200-16=80(人).
补全的统计图如图.
家长对“中学生带手机到学校”态度的条形统计图
故题图(2)中表示家长“基本赞成”的圆心角的度数为72°.
(3)样本中,被调查的400名家长中,“无所谓”的有16名,所以随机抽查一个,恰好是“无所谓”态度的家长的概率是
故随机抽查一个,恰好是“无所谓”态度的家长的概率是
25.(1)0.95 (2)0.95
(3)1200×0.95=1140(人).
故佩戴了头盔的骑行者大约有1 140人.
26.(1)0.3 [解析]由表知,转动该转盘一次,获得铅笔的概率约为0.7,所以获得饮料的概率约为0.3.
(2)设该商场每支铅笔x元,每瓶饮料(4-x)元.
根据题意,得5000×(4-x)×0.3+5000x×0.7=8000,解得x=1,则4-x=4-1=3.
故该商场每支铅笔1元,每瓶饮料3元.
(3)36 [解析]设转盘上“一瓶饮料”区域的圆心角应调整为n度,则 解得n=36.
故转盘上“一瓶饮料”区域的圆心角应调整为36°.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
