期中提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 期中提优测评卷 (含答案)2024-2025学年苏科版八年级数学下册 | 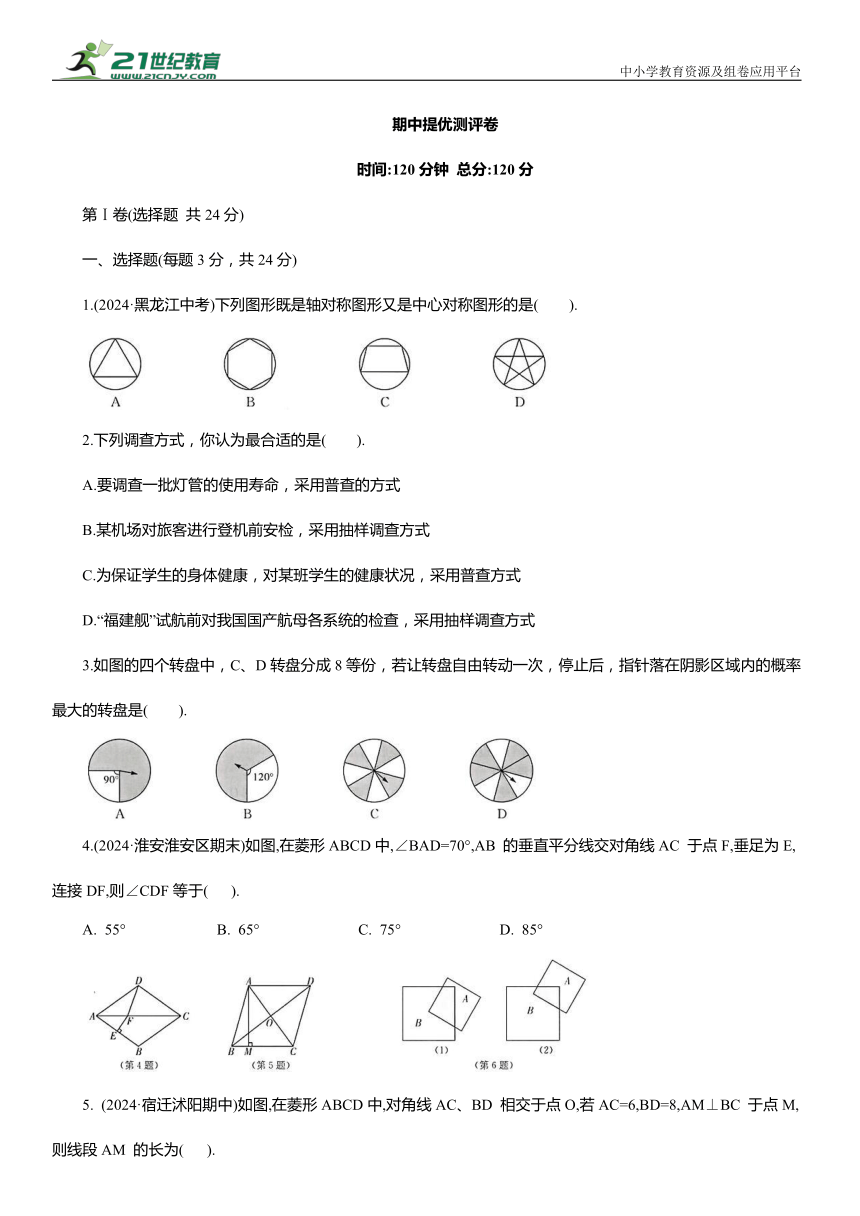 | |
| 格式 | docx | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 05:16:52 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
期中提优测评卷
时间:120分钟 总分:120分
第Ⅰ卷(选择题 共24分)
一、选择题(每题3分,共24分)
1.(2024·黑龙江中考)下列图形既是轴对称图形又是中心对称图形的是( ).
2.下列调查方式,你认为最合适的是( ).
A.要调查一批灯管的使用寿命,采用普查的方式
B.某机场对旅客进行登机前安检,采用抽样调查方式
C.为保证学生的身体健康,对某班学生的健康状况,采用普查方式
D.“福建舰”试航前对我国国产航母各系统的检查,采用抽样调查方式
3.如图的四个转盘中,C、D转盘分成8等份,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( ).
4.(2024·淮安淮安区期末)如图,在菱形ABCD中,∠BAD=70°,AB 的垂直平分线交对角线AC 于点F,垂足为E,连接DF,则∠CDF等于( ).
A. 55° B. 65° C. 75° D. 85°
5. (2024·宿迁沭阳期中)如图,在菱形ABCD中,对角线AC、BD 相交于点O,若AC=6,BD=8,AM⊥BC 于点M,则线段AM 的长为( ).
A. 2.4 B. 4.8 C. 5 D. 5.6
6.如图(1),正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的 ,如图(2),移动正方形A 的位置,使正方形 B 的一个顶点与正方形A 的对称中心重合,则重叠部分面积是正方形 B 面积的( ).
A. B. C. D.
7.(2024·南通启东期末)相关部门对“五一”期间到某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图(如图),根据图中信息,下列结论不正确的是( ).
A.本次抽样调查的样本容量是500
B.扇形统计图中“其他”的占比为10%
C.样本中选择公共交通出行的有250人
D.若“五一”期间到该景点观光的游客有50万人,则选择自驾出行的约有25万人
8.(2023·重庆中考改编)如图,在正方形ABCD中,O为对角线AC的中点,E 为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE 的平分线交于点F,连接OF,若AB= ,则OF的长度为( ).
A. 2 B. C. 1 D.
第Ⅱ卷(非选择题 共96分)
二、填空题(每题3分,共30分)
9.(2023·苏州吴江区期中)妈妈做菜时,为了了解菜品的咸淡是否合适,取了一点品尝,妈妈的做法属于 .(从“普查”或“抽样调查”中选一)
10.一个不透明的袋里装有除颜色外其他完全相同的10个小球,其中有6个黄球,3个白球,1个黑球,将袋中的球摇匀,从中任意摸出一个球,摸出 球的可能性最大.
11.(2024·宿迁三模)在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6、8、9、12,第五组的频率是0.1,则第六组的频数是 .
12.如图是某冷饮店一天售出各种口味雪糕数量的扇形统计图,其中售出奶油口味的雪糕150支,则售出红豆口味雪糕的数量是 支.
13.某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x/小时 0≤x≤1 13
人数 7 10 14 19
14. 如图,在 ABCD中,∠A=70°,将 ABCD绕顶点B 顺时针旋转到 A BC D ,当C D 首次经过顶点C时,旋转角的度数为 .
15.(2023·荆州中考)如图,CD为Rt△ABC斜边AB上的中线,E为AC 的中点.若AC=8,CD=5,则DE= .
16.(2024·常州溧阳期末)如图,在平行四边形ABCD 中,AE 是边DC 上的高,AE=4,点 P、Q分别是AD、EC的中点,DC=6,则PQ的长为 .
17.(2024·广东中考)如图,菱形ABCD 的面积为24,点E 是AB 的中点,点 F 是BC上的动点.若△BEF 的面积为4,则图中阴影部分的面积为 .
18. 如图,在矩形ABCD中,AB=1,AD=2,E为BC的中点,F为DE上一动点,P为AF 的中点,连接PC,则 PC 的最小值是 .
三、解答题(第19~22题每题7分,第23、24题每题9分,第25、26题每题10分,共66分)
19.如图,在平面直角坐标系中,△ABC 的三个顶点坐标都在格点上,且△A B C 与△ABC关于原点O成中心对称.
(1)请直接写出A 的坐标为 ,并画出△A B C ;
(2)P(a,b)是△ABC的边AC上一点,将△ABC平移后点P 的对应点 请画出平移后的△A B C ;
(3)若△A B C 和△A B C 关于某一点成中心对称,则对称中心的坐标为 .
20.新情境关注视力健康(2023·怀化中考)近年,“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了两幅不完整的统计图.请根据图中信息解答下列问题:
(1)所抽取的学生人数为 ;
(2)补全条形统计图,并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数;
(3)该校共有学生3 000人,请估计该校学生中近视程度为“轻度近视”的人数.
21.一个不透明的袋子里装有黑白两种颜色的球若干个,这些球除颜色外都相同.从袋子中随机摸一个球,记下颜色后放回搅匀,不断重复上面的过程,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到白球的概率估计值为 (精确到0.1).
(2)若袋子中白球有4个,
①求袋中黑色球的个数;
②若将m 个相同的白球放进了这个不透明的袋子里,然后再次进行摸球试验,当大量重复试验后,摸出白球的概率估计值是 .(用含m的式子表示)
22. (2023·南充中考)如图,在 中,点E、F在对角线AC上, 求证:
23. (2024·常州模拟)如图,已知 求证:
(2)四边形BCEF 是矩形.
24. (2024·南京建邺区致远初中期中)如图,在平行四边形ABCD中,E、F 为对角线BD上两点, DF,连接AE、EC、CF、FA.
(1)求证:四边形AECF 为平行四边形;
(2)若 求证:四边形AECF 为菱形;
(3)在(2)的条件下,连接AC交BD于点O,若AB:BE:AO 求证:四边形AECF 为正方形.
25.如图,点A 在直线l外,点B 在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若 且点 A 到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.
26.中考新考法 新定义问题 若四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫作这个四边形的“巧分线”,这个四边形叫“巧妙四边形”,若一个四边形有两条巧分线,则称为“绝妙四边形”.
(1)下列四边形一定是巧妙四边形的是 .(填序号)
①平行四边形;②矩形;③菱形;④正方形.
初步应用
(2)在绝妙四边形ABCD中,AC垂直平分BD,若∠BAD=80°,则
深入研究
(3)如图,在梯形ABCD中,AD∥BC,AB=AD=CD,∠B=72°.
求证:梯形ABCD 是绝妙四边形.
(4)在巧妙四边形ABCD中,AB=AD=CD,∠A=90°,AC是四边形ABCD的巧分线,请直接写出∠BCD的度数.
期中提优测评卷
1. B [解析]A.是轴对称图形,不是中心对称图形,不符合题意;B.既是轴对称图形,又是中心对称图形,符合题意;C.是轴对称图形,不是中心对称图形,不符合题意;D.是轴对称图形,不是中心对称图形,不符合题意.故选 B.
2. C [解析]A.要调查一批灯管的使用寿命,适合采用抽样调查方式,不符合题意;B.某机场对旅客进行登机前安检,适合采用全面调查方式,不符合题意;C.为保证学生的身体健康,对某班学生的健康状况,适合采用全面调查方式,符合题意;D.“福建舰”试航前对我国国产航母各系统的检查,适合采用全面调查方式,不符合题意.故选 C.
3. A [解析]依次计算得 故选 A.
4. C
5. B [解析]∵四边形 ABCD 是菱形,
∴BO=DO,AO=CO,AC⊥BD.
∵AC=6,BD=8,∴OC=3,OB=4,
∴BC·AM=24,∴AM=4.8.故选 B.
6. D [解析]由题图(1)可得 即 则由题图(2)可得 故选 D.
7. D [解析]A.本次抽样调查的样本容量是 200÷40%=500,此选项不符合题意;B.扇形统计图中“其他”的占比为1—(50%+40%)=10%,此选项不符合题意;C.样本中选择公共交通出行的有 500×50%=250(人),此选项不符合题意;D.若“五一”期间观光的游客有50万人,则选择自驾出行的有50×40%=20(万人),此选项符合题意.故选 D.
8. C [解析]连接AF,
∵四边形ABCD 是正方形,
∴AB=BE=BC,∠ABC=90°,AC=2,
∴∠BEC=∠BCE,∴∠EBC=180°-2∠BEC,
∴∠ABE=∠ABC-∠EBC=2∠BEC-90°.
∵BF平分∠A
∴∠BFE=∠BEC-∠EBF=45°.
在△BAF与△BEF 中,
∴△BAF≌△BEF(SAS),∴∠BFE=∠BFA=45°,∴∠AFC=∠BFA+∠BFE=90°.
∵O为对角线AC 的中点, 故选C.
9.抽样调查 10.黄
11.10 [解析]∵一个容量为50的样本分成6组,第一组到第四组的频数分别为6、8、9、12,第五组的频率是0.1,则第五组的频数是0.1×50=5,∴第六组的频数是50-6-8-9-12-5=10.
12.200 [解析]售出的红豆口味雪糕的数量为150÷30%×40%=200(支).
13.680 [解析] 680(人).
14.40° [解析]∵四边形ABCD 为平行四边形,∴∠A=∠BCD=70°.
由旋转可得
.故旋转角为40°.
15.3 [解析]∵CD 为 Rt△ABC 斜边AB 上的中线,CD=5,∴AB=2CD=10.
∵∠ACB=90°,AC=8,
∵E为AC的中点,∴AE=CE,
∴DE 是△ABC的中位线,
[解析]如图,取D E的 中点F,连接P F,则
∵AE 是平行四边形ABCD的边 DC 上的高,AE=4,
∴AE⊥CD.
∵点 P 是AD的中点,
∴∠PFQ=∠AEC=90°.
∵点 Q是EC的中点,
17.10 [解析]连接 BD、CE,因为 E 是AB 的中点,所以 菱形ABCD =6,S△BEC =S△AED=6,根据 可得 故 故
18. [解析]如图,取AD的中点H,连接BH、CH,设BH 与AE 的交点为O,连接CO,
∵四边形ABCD 是矩形,∴AB=CD=1,AD=BC=2,AD∥BC,∠BAH=∠CDH=90°.
∵点E 是BC 的中点,点 H 是AD 的中点,
∴AH=CE=DH=BE=AB=CD=1.
∴四边形 BEDH 是平行四边形,∠AHB=∠ABH=
∴BH∥DE.
∵点 P 是AF 的中点,点 H 是AD 的中点,
∴PH∥ED,∴点 P 在BH 上.
∵∠AHB=∠DHC=45°,
∴BH⊥CH.
∵点P 在BH 上,∴当CP⊥BH 时,此时点 P 与H 重合,PC有最小值.
在 Rt△CDH 中,
∴PC的最小值为
19.(1)(3,—4) △A B C 如图所示.
(2)如图所示,△A B C 即为所求.
(3)(1,-3)
20.(1)200 [解析]所抽取的学生人数:90÷45%=200(名).
(2)样本中“中度近视”的人数:200×15%=30(名),“高度近视”的人数:200-90-70-30=10(名).补全条形统计图如图:
扇形统计图中“轻度近视”对应的扇形的圆心角的度数:
(名).
故估计该校学生中近视程度为“轻度近视”的人数约1050人.
21.(1)0.2 [解析]由题图可以看出,随着摸球次数的增多,摸到白球的频率在0.20左右摆动.根据频率与概率的关系,可知摸到白球的概率为0.2.
(2)①∵袋子中白球有4个,
∴袋中球的总个数为4÷0.2=20.
∴袋中黑色球的个数为20-4=16.
[解析]∵将m 个相同的白球放进了这个不透明的袋子里.
∴袋中白球的个数为4+m,袋中球的总个数为20+m.∴摸到白球的概率估计值为
22.(1)∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC,∴∠DAF=∠BCE.
在△ADF 与△CBE 中
∴△ADF≌△CBE(ASA),∴AF=CE,
∴AF--EF=CE-EF,∴AE=CF.
(2)∵△ADF≌△CBE,
∴∠AFD=∠CEB,∴BE∥DF.
23.(1)∵AB∥DE,∴∠A=∠D.
∵AC=FD,
∴AC-CF=DF-CF,
即AF=CD.
在△ABF 与△DEC中
∴△ABF≌△DEC(SAS).
(2)∵△ABF≌△DEC,
∴EC=BF,∠ECD=∠BFA,
∴∠ECF=∠BFC,
∴EC∥BF,
∴四边形 BCEF 为平行四边形.
∵∠CEF=90°,∴四边形 BCEF 是矩形.
24.(1)连接AC交BD 于点O,如图.
在□ABCD中,OA=OC,OB=OD.
∵BE=DF,∴OB-BE=OD--DF,即OE=OF,
∴四边形AECF 是平行四边形.
(2)在 ABCD中,
∵AB=AD,
∴□ABCD 是菱形,∴AC⊥BD,∴AC⊥EF,
∴平行四边形AECF 是菱形.
(3)在(2)的条件下∠AOB=90°,
∵AB:BE:AO=5:1:3,
设AB=5k,则AO=3k,BE=k,
由勾股定理得BO=4k,∴EO=BO-BE=3k,
∴AO=EO,∴AO=EO=OF,
∴∠OAE=∠OEA=45°,∠OAF=∠OFA=45°,
∴∠EAF=∠OAE+∠OAF=90°.
∵四边形 AECF 是菱形.
∴四边形 AECF 是正方形.
25.(1)如图(1)(2)(3)所示.
(2)图(1)中,菱形ABCD 的面积=5×4=20.
图(2)中,BC=6,AD=8,
则菱形ABDC的面积
图(3)中,作AH⊥BC 于点H,设菱形的边长为x,在Rt△ABH 中,AH=4,AB=5,则 BH=3,所以CH=x-3.
在Rt△ACH 中, 解得
则菱形ACBD 的面积
所以面积最小的为菱形ACBD.
26.(1)③④ [解析]∵菱形的四条边相等,
∴连接对角线能得到两个等腰三角形.
∴菱形是巧妙四边形.∵正方形是特殊的菱形,
∴正方形也是巧妙四边形.
(2)140°或80° [解析]分两种情况:
①当AC=AD=AB时,如图(1),
∵AC垂直平分BD,
∴AB=AD,BC=CD,AC⊥BD.
∴∠BAC=∠DAC.
∵∠BAD=80°,∴∠BAC=∠DAC=40°.
∵AC=AD=AB,∴∠ACD=∠ADC=∠ACB=
∴∠BCD=2∠ACD=140°.
②当AD=CD,AB=BC时,如图(2),
∵AC垂直平分BD,
∴AB=AD,BC=CD,AC⊥BD.
∴AB=AD=CD=BC.
∴四边形 ABCD 是菱形.∴∠BCD=∠BAD=80°.
综上所述,∠BCD=140°或80°.
(3)如图(3),连接AC与BD,交于点O,在梯形ABCD中,AB=CD,
∴∠ABC=∠DCB=72°.
∵AD∥BC,∴∠BAD=∠ADC=108°.
∵AB=AD=CD,
∴△ABD是等腰三角形,∠ABD=∠ADB=36°.
72°=∠DCB.∴△BDC 也是等腰三角形.
∴对角线 BD 是这个四边形ABCD 的巧分线.同理可得△ADC 和△ACB 也是等腰三角形,
∴对角线 AC 是这个四边形ABCD的巧分线.
∴梯形 ABCD 是绝妙四边形.
(4)∵AC 是四边形ABCD的巧分线,
∴△ACD 和△ABC 是等腰三角形.
①当AC=BC时,如图(4),过点 C作CH⊥AB 于点H,过点C作CG⊥AD,交AD的延长线于点G,
∵∠HAD=∠AHC=∠G=90°,
∴四边形AHCG 是矩形,
∴∠ADC=150°,∴∠DAC=∠DCA=15°.
∵∠DAB=90°,∴∠CAB=∠B=75°.
∴∠ACB=30°,∴∠BCD=30°+15°=45°.
②当AC=AB时,如图(5),
∵AC=AB=AD=CD,∴△ACD是等边三角形.
∴∠CAD=∠ACD=60°.
∵∠BAD=90°,∴∠BAC=30°.
∵AB=AC,∴∠ACB=75°.
③当AB=BC时,如图(6),此时∠BCD=90°.综上所述,∠BCD 的度数是45°或135°或90°.
期中提优测评卷
时间:120分钟 总分:120分
第Ⅰ卷(选择题 共24分)
一、选择题(每题3分,共24分)
1.(2024·黑龙江中考)下列图形既是轴对称图形又是中心对称图形的是( ).
2.下列调查方式,你认为最合适的是( ).
A.要调查一批灯管的使用寿命,采用普查的方式
B.某机场对旅客进行登机前安检,采用抽样调查方式
C.为保证学生的身体健康,对某班学生的健康状况,采用普查方式
D.“福建舰”试航前对我国国产航母各系统的检查,采用抽样调查方式
3.如图的四个转盘中,C、D转盘分成8等份,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( ).
4.(2024·淮安淮安区期末)如图,在菱形ABCD中,∠BAD=70°,AB 的垂直平分线交对角线AC 于点F,垂足为E,连接DF,则∠CDF等于( ).
A. 55° B. 65° C. 75° D. 85°
5. (2024·宿迁沭阳期中)如图,在菱形ABCD中,对角线AC、BD 相交于点O,若AC=6,BD=8,AM⊥BC 于点M,则线段AM 的长为( ).
A. 2.4 B. 4.8 C. 5 D. 5.6
6.如图(1),正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的 ,如图(2),移动正方形A 的位置,使正方形 B 的一个顶点与正方形A 的对称中心重合,则重叠部分面积是正方形 B 面积的( ).
A. B. C. D.
7.(2024·南通启东期末)相关部门对“五一”期间到某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图(如图),根据图中信息,下列结论不正确的是( ).
A.本次抽样调查的样本容量是500
B.扇形统计图中“其他”的占比为10%
C.样本中选择公共交通出行的有250人
D.若“五一”期间到该景点观光的游客有50万人,则选择自驾出行的约有25万人
8.(2023·重庆中考改编)如图,在正方形ABCD中,O为对角线AC的中点,E 为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE 的平分线交于点F,连接OF,若AB= ,则OF的长度为( ).
A. 2 B. C. 1 D.
第Ⅱ卷(非选择题 共96分)
二、填空题(每题3分,共30分)
9.(2023·苏州吴江区期中)妈妈做菜时,为了了解菜品的咸淡是否合适,取了一点品尝,妈妈的做法属于 .(从“普查”或“抽样调查”中选一)
10.一个不透明的袋里装有除颜色外其他完全相同的10个小球,其中有6个黄球,3个白球,1个黑球,将袋中的球摇匀,从中任意摸出一个球,摸出 球的可能性最大.
11.(2024·宿迁三模)在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6、8、9、12,第五组的频率是0.1,则第六组的频数是 .
12.如图是某冷饮店一天售出各种口味雪糕数量的扇形统计图,其中售出奶油口味的雪糕150支,则售出红豆口味雪糕的数量是 支.
13.某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x/小时 0≤x≤1 1
人数 7 10 14 19
14. 如图,在 ABCD中,∠A=70°,将 ABCD绕顶点B 顺时针旋转到 A BC D ,当C D 首次经过顶点C时,旋转角的度数为 .
15.(2023·荆州中考)如图,CD为Rt△ABC斜边AB上的中线,E为AC 的中点.若AC=8,CD=5,则DE= .
16.(2024·常州溧阳期末)如图,在平行四边形ABCD 中,AE 是边DC 上的高,AE=4,点 P、Q分别是AD、EC的中点,DC=6,则PQ的长为 .
17.(2024·广东中考)如图,菱形ABCD 的面积为24,点E 是AB 的中点,点 F 是BC上的动点.若△BEF 的面积为4,则图中阴影部分的面积为 .
18. 如图,在矩形ABCD中,AB=1,AD=2,E为BC的中点,F为DE上一动点,P为AF 的中点,连接PC,则 PC 的最小值是 .
三、解答题(第19~22题每题7分,第23、24题每题9分,第25、26题每题10分,共66分)
19.如图,在平面直角坐标系中,△ABC 的三个顶点坐标都在格点上,且△A B C 与△ABC关于原点O成中心对称.
(1)请直接写出A 的坐标为 ,并画出△A B C ;
(2)P(a,b)是△ABC的边AC上一点,将△ABC平移后点P 的对应点 请画出平移后的△A B C ;
(3)若△A B C 和△A B C 关于某一点成中心对称,则对称中心的坐标为 .
20.新情境关注视力健康(2023·怀化中考)近年,“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了两幅不完整的统计图.请根据图中信息解答下列问题:
(1)所抽取的学生人数为 ;
(2)补全条形统计图,并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数;
(3)该校共有学生3 000人,请估计该校学生中近视程度为“轻度近视”的人数.
21.一个不透明的袋子里装有黑白两种颜色的球若干个,这些球除颜色外都相同.从袋子中随机摸一个球,记下颜色后放回搅匀,不断重复上面的过程,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到白球的概率估计值为 (精确到0.1).
(2)若袋子中白球有4个,
①求袋中黑色球的个数;
②若将m 个相同的白球放进了这个不透明的袋子里,然后再次进行摸球试验,当大量重复试验后,摸出白球的概率估计值是 .(用含m的式子表示)
22. (2023·南充中考)如图,在 中,点E、F在对角线AC上, 求证:
23. (2024·常州模拟)如图,已知 求证:
(2)四边形BCEF 是矩形.
24. (2024·南京建邺区致远初中期中)如图,在平行四边形ABCD中,E、F 为对角线BD上两点, DF,连接AE、EC、CF、FA.
(1)求证:四边形AECF 为平行四边形;
(2)若 求证:四边形AECF 为菱形;
(3)在(2)的条件下,连接AC交BD于点O,若AB:BE:AO 求证:四边形AECF 为正方形.
25.如图,点A 在直线l外,点B 在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若 且点 A 到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.
26.中考新考法 新定义问题 若四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫作这个四边形的“巧分线”,这个四边形叫“巧妙四边形”,若一个四边形有两条巧分线,则称为“绝妙四边形”.
(1)下列四边形一定是巧妙四边形的是 .(填序号)
①平行四边形;②矩形;③菱形;④正方形.
初步应用
(2)在绝妙四边形ABCD中,AC垂直平分BD,若∠BAD=80°,则
深入研究
(3)如图,在梯形ABCD中,AD∥BC,AB=AD=CD,∠B=72°.
求证:梯形ABCD 是绝妙四边形.
(4)在巧妙四边形ABCD中,AB=AD=CD,∠A=90°,AC是四边形ABCD的巧分线,请直接写出∠BCD的度数.
期中提优测评卷
1. B [解析]A.是轴对称图形,不是中心对称图形,不符合题意;B.既是轴对称图形,又是中心对称图形,符合题意;C.是轴对称图形,不是中心对称图形,不符合题意;D.是轴对称图形,不是中心对称图形,不符合题意.故选 B.
2. C [解析]A.要调查一批灯管的使用寿命,适合采用抽样调查方式,不符合题意;B.某机场对旅客进行登机前安检,适合采用全面调查方式,不符合题意;C.为保证学生的身体健康,对某班学生的健康状况,适合采用全面调查方式,符合题意;D.“福建舰”试航前对我国国产航母各系统的检查,适合采用全面调查方式,不符合题意.故选 C.
3. A [解析]依次计算得 故选 A.
4. C
5. B [解析]∵四边形 ABCD 是菱形,
∴BO=DO,AO=CO,AC⊥BD.
∵AC=6,BD=8,∴OC=3,OB=4,
∴BC·AM=24,∴AM=4.8.故选 B.
6. D [解析]由题图(1)可得 即 则由题图(2)可得 故选 D.
7. D [解析]A.本次抽样调查的样本容量是 200÷40%=500,此选项不符合题意;B.扇形统计图中“其他”的占比为1—(50%+40%)=10%,此选项不符合题意;C.样本中选择公共交通出行的有 500×50%=250(人),此选项不符合题意;D.若“五一”期间观光的游客有50万人,则选择自驾出行的有50×40%=20(万人),此选项符合题意.故选 D.
8. C [解析]连接AF,
∵四边形ABCD 是正方形,
∴AB=BE=BC,∠ABC=90°,AC=2,
∴∠BEC=∠BCE,∴∠EBC=180°-2∠BEC,
∴∠ABE=∠ABC-∠EBC=2∠BEC-90°.
∵BF平分∠A
∴∠BFE=∠BEC-∠EBF=45°.
在△BAF与△BEF 中,
∴△BAF≌△BEF(SAS),∴∠BFE=∠BFA=45°,∴∠AFC=∠BFA+∠BFE=90°.
∵O为对角线AC 的中点, 故选C.
9.抽样调查 10.黄
11.10 [解析]∵一个容量为50的样本分成6组,第一组到第四组的频数分别为6、8、9、12,第五组的频率是0.1,则第五组的频数是0.1×50=5,∴第六组的频数是50-6-8-9-12-5=10.
12.200 [解析]售出的红豆口味雪糕的数量为150÷30%×40%=200(支).
13.680 [解析] 680(人).
14.40° [解析]∵四边形ABCD 为平行四边形,∴∠A=∠BCD=70°.
由旋转可得
.故旋转角为40°.
15.3 [解析]∵CD 为 Rt△ABC 斜边AB 上的中线,CD=5,∴AB=2CD=10.
∵∠ACB=90°,AC=8,
∵E为AC的中点,∴AE=CE,
∴DE 是△ABC的中位线,
[解析]如图,取D E的 中点F,连接P F,则
∵AE 是平行四边形ABCD的边 DC 上的高,AE=4,
∴AE⊥CD.
∵点 P 是AD的中点,
∴∠PFQ=∠AEC=90°.
∵点 Q是EC的中点,
17.10 [解析]连接 BD、CE,因为 E 是AB 的中点,所以 菱形ABCD =6,S△BEC =S△AED=6,根据 可得 故 故
18. [解析]如图,取AD的中点H,连接BH、CH,设BH 与AE 的交点为O,连接CO,
∵四边形ABCD 是矩形,∴AB=CD=1,AD=BC=2,AD∥BC,∠BAH=∠CDH=90°.
∵点E 是BC 的中点,点 H 是AD 的中点,
∴AH=CE=DH=BE=AB=CD=1.
∴四边形 BEDH 是平行四边形,∠AHB=∠ABH=
∴BH∥DE.
∵点 P 是AF 的中点,点 H 是AD 的中点,
∴PH∥ED,∴点 P 在BH 上.
∵∠AHB=∠DHC=45°,
∴BH⊥CH.
∵点P 在BH 上,∴当CP⊥BH 时,此时点 P 与H 重合,PC有最小值.
在 Rt△CDH 中,
∴PC的最小值为
19.(1)(3,—4) △A B C 如图所示.
(2)如图所示,△A B C 即为所求.
(3)(1,-3)
20.(1)200 [解析]所抽取的学生人数:90÷45%=200(名).
(2)样本中“中度近视”的人数:200×15%=30(名),“高度近视”的人数:200-90-70-30=10(名).补全条形统计图如图:
扇形统计图中“轻度近视”对应的扇形的圆心角的度数:
(名).
故估计该校学生中近视程度为“轻度近视”的人数约1050人.
21.(1)0.2 [解析]由题图可以看出,随着摸球次数的增多,摸到白球的频率在0.20左右摆动.根据频率与概率的关系,可知摸到白球的概率为0.2.
(2)①∵袋子中白球有4个,
∴袋中球的总个数为4÷0.2=20.
∴袋中黑色球的个数为20-4=16.
[解析]∵将m 个相同的白球放进了这个不透明的袋子里.
∴袋中白球的个数为4+m,袋中球的总个数为20+m.∴摸到白球的概率估计值为
22.(1)∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC,∴∠DAF=∠BCE.
在△ADF 与△CBE 中
∴△ADF≌△CBE(ASA),∴AF=CE,
∴AF--EF=CE-EF,∴AE=CF.
(2)∵△ADF≌△CBE,
∴∠AFD=∠CEB,∴BE∥DF.
23.(1)∵AB∥DE,∴∠A=∠D.
∵AC=FD,
∴AC-CF=DF-CF,
即AF=CD.
在△ABF 与△DEC中
∴△ABF≌△DEC(SAS).
(2)∵△ABF≌△DEC,
∴EC=BF,∠ECD=∠BFA,
∴∠ECF=∠BFC,
∴EC∥BF,
∴四边形 BCEF 为平行四边形.
∵∠CEF=90°,∴四边形 BCEF 是矩形.
24.(1)连接AC交BD 于点O,如图.
在□ABCD中,OA=OC,OB=OD.
∵BE=DF,∴OB-BE=OD--DF,即OE=OF,
∴四边形AECF 是平行四边形.
(2)在 ABCD中,
∵AB=AD,
∴□ABCD 是菱形,∴AC⊥BD,∴AC⊥EF,
∴平行四边形AECF 是菱形.
(3)在(2)的条件下∠AOB=90°,
∵AB:BE:AO=5:1:3,
设AB=5k,则AO=3k,BE=k,
由勾股定理得BO=4k,∴EO=BO-BE=3k,
∴AO=EO,∴AO=EO=OF,
∴∠OAE=∠OEA=45°,∠OAF=∠OFA=45°,
∴∠EAF=∠OAE+∠OAF=90°.
∵四边形 AECF 是菱形.
∴四边形 AECF 是正方形.
25.(1)如图(1)(2)(3)所示.
(2)图(1)中,菱形ABCD 的面积=5×4=20.
图(2)中,BC=6,AD=8,
则菱形ABDC的面积
图(3)中,作AH⊥BC 于点H,设菱形的边长为x,在Rt△ABH 中,AH=4,AB=5,则 BH=3,所以CH=x-3.
在Rt△ACH 中, 解得
则菱形ACBD 的面积
所以面积最小的为菱形ACBD.
26.(1)③④ [解析]∵菱形的四条边相等,
∴连接对角线能得到两个等腰三角形.
∴菱形是巧妙四边形.∵正方形是特殊的菱形,
∴正方形也是巧妙四边形.
(2)140°或80° [解析]分两种情况:
①当AC=AD=AB时,如图(1),
∵AC垂直平分BD,
∴AB=AD,BC=CD,AC⊥BD.
∴∠BAC=∠DAC.
∵∠BAD=80°,∴∠BAC=∠DAC=40°.
∵AC=AD=AB,∴∠ACD=∠ADC=∠ACB=
∴∠BCD=2∠ACD=140°.
②当AD=CD,AB=BC时,如图(2),
∵AC垂直平分BD,
∴AB=AD,BC=CD,AC⊥BD.
∴AB=AD=CD=BC.
∴四边形 ABCD 是菱形.∴∠BCD=∠BAD=80°.
综上所述,∠BCD=140°或80°.
(3)如图(3),连接AC与BD,交于点O,在梯形ABCD中,AB=CD,
∴∠ABC=∠DCB=72°.
∵AD∥BC,∴∠BAD=∠ADC=108°.
∵AB=AD=CD,
∴△ABD是等腰三角形,∠ABD=∠ADB=36°.
72°=∠DCB.∴△BDC 也是等腰三角形.
∴对角线 BD 是这个四边形ABCD 的巧分线.同理可得△ADC 和△ACB 也是等腰三角形,
∴对角线 AC 是这个四边形ABCD的巧分线.
∴梯形 ABCD 是绝妙四边形.
(4)∵AC 是四边形ABCD的巧分线,
∴△ACD 和△ABC 是等腰三角形.
①当AC=BC时,如图(4),过点 C作CH⊥AB 于点H,过点C作CG⊥AD,交AD的延长线于点G,
∵∠HAD=∠AHC=∠G=90°,
∴四边形AHCG 是矩形,
∴∠ADC=150°,∴∠DAC=∠DCA=15°.
∵∠DAB=90°,∴∠CAB=∠B=75°.
∴∠ACB=30°,∴∠BCD=30°+15°=45°.
②当AC=AB时,如图(5),
∵AC=AB=AD=CD,∴△ACD是等边三角形.
∴∠CAD=∠ACD=60°.
∵∠BAD=90°,∴∠BAC=30°.
∵AB=AC,∴∠ACB=75°.
③当AB=BC时,如图(6),此时∠BCD=90°.综上所述,∠BCD 的度数是45°或135°或90°.
同课章节目录
