9.3 平行四边形 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 9.3 平行四边形 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 416.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 00:00:00 | ||
图片预览



文档简介
9.3 平行四边形
第 1课时 平行四边形(1)
1.如图,在平行四边形 ABCD中,AE 平分∠BAD 且交 BC 于点 E,∠D=58°,则∠AEC 的度数是( ).
A. 61°B. 109°C. 112°D. 119°
2.(2024·无锡宜兴模拟)在平行四边形 ABCD 中,∠B+∠D=100°,则∠A 等于( ).
A. 50°B. 130°C. 100°D. 65°
3.如图,在平行四边形 ABCD 中,AC、BD 相交于点 O,∠ODA = 90°,AC =10 cm,BD =6cm,则 BC 的长为( ).
A. 4 cm B. 5cm C. 6 cm D. 8cm
4.(2024·苏州姑苏区期中)如图,在□ABCD 中,已知AD=8cm,AB=5cm ,DE 平分∠ADC 交BC 边于点E,则 BE 等于( ).
A. 1cm B. 2cm C. 3cm D. 4cm
5. 在 ABCD中,对角线AC 和 BD 相交于点 O,如果AC=10,BD=6,AB=m,那么m的取值范围是( ).
A. 1C. 66.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC 是□ABCD 的对角线,点E 在AC上,AD=AE=BE,∠D=102°,则∠BAC 的大小是 .
7.如图,在平面直角坐标系中,□ABCD 的顶点坐标分别是A(0,1)、B(a,b)、C(3,-2),则D的坐标是( ).
A. (-a+3,-b+1)
B. (-a--3,-b--1)
C. (-a-3,-b+1)
D. (-a+3,-b--1)
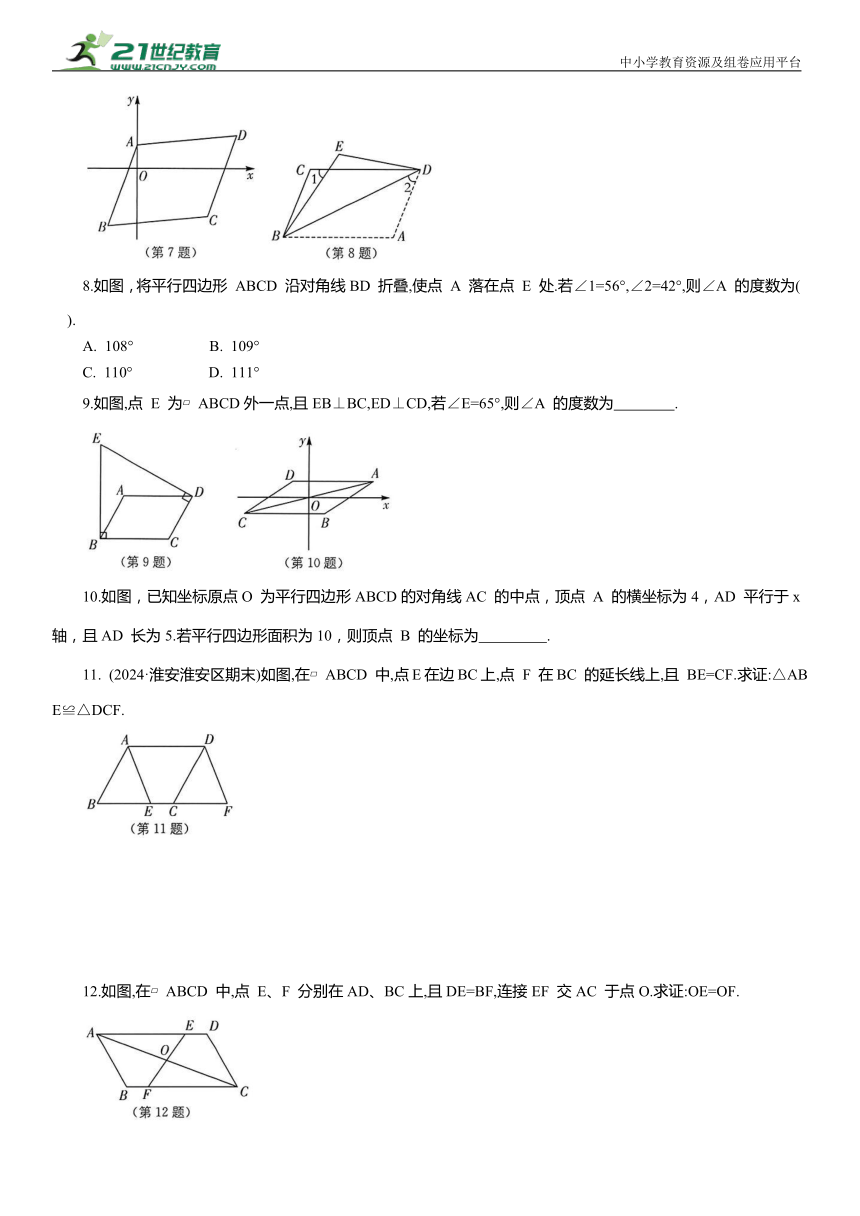
8.如图,将平行四边形 ABCD 沿对角线BD 折叠,使点 A 落在点 E 处.若∠1=56°,∠2=42°,则∠A 的度数为( ).
A. 108° B. 109°
C. 110° D. 111°
9.如图,点 E 为 ABCD外一点,且EB⊥BC,ED⊥CD,若∠E=65°,则∠A 的度数为 .
10.如图,已知坐标原点O 为平行四边形ABCD的对角线AC 的中点,顶点 A 的横坐标为4,AD 平行于x轴,且AD 长为5.若平行四边形面积为10,则顶点 B 的坐标为 .
11. (2024·淮安淮安区期末)如图,在 ABCD 中,点E在边BC上,点 F 在BC 的延长线上,且 BE=CF.求证:△ABE≌△DCF.
12.如图,在 ABCD 中,点 E、F 分别在AD、BC上,且DE=BF,连接EF 交AC 于点O.求证:OE=OF.
13.已知:平行四边形ABCD中,对角线AC、BD 相交于点O,BD=2AD,E、F、G分别是OC、OD、AB 的中点.求证:BE⊥AC.
14. 如图,在□ABCD 中,AE 平分∠BAD,交 BC 于点 E,CF 平分∠BCD,交AD 于点 F.求证:AE=CF.
15.如图,在平行四边形 ABCD 中,点 E、F 分别在边BC、AD上,EA⊥AC,FC⊥AC.
(1)求证:△ABE≌△CDF;
(2)若∠B=30°,∠AEC=45°,求证:AB=AF.
中小学教育资源及组卷应用平台
第2课时 平行四边形(2)
1.(2024·乐山中考)如图,下列条件中不能判定四边形 ABCD 为平行四边形的是( ).
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
2.(2024·辽宁中考)如图,□ABCD 的对角线AC、BD 相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED 的周长为( ).
A. 4 B. 6 C. 8 D. 16
3.中考新考法 满足结论的条件开放 (2024·镇江丹阳期中)如图,在四边形 ABCD 中,AC 与 BD 相交于点O,AO=CO,添加条件 ,可得四边形 ABCD 为平行四边形(只需添加一个条件).
4. 教材P69例3·变式(2024·苏州姑苏区期末)如图,点E、F 是□ABCD 对角线上两点,且 DE=BF,连接AE、AF、CE、CF.求证:四边形 AECF为平行四边形.
5.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( ).
A. ①② B. ①④
C. ③④ D. ②③
6.如图,在△ABC 中,点 D、E 分别是AB、AC 上的点,且DE∥BC,点 F 是 DE 延长线上一点,连接CF.添加下列条件:①BD∥CF;②DF=BC;③BD=CF;④∠B=∠F.能使四边形BCFD 是平行四边形的是 (填上所有符合要求的条件的序号).
7.如图,点 E、F、G、H 分别是平行四边形ABCD 各边的中点,连接AF、CE相交于点M,连接AG、CH 相交于点N.
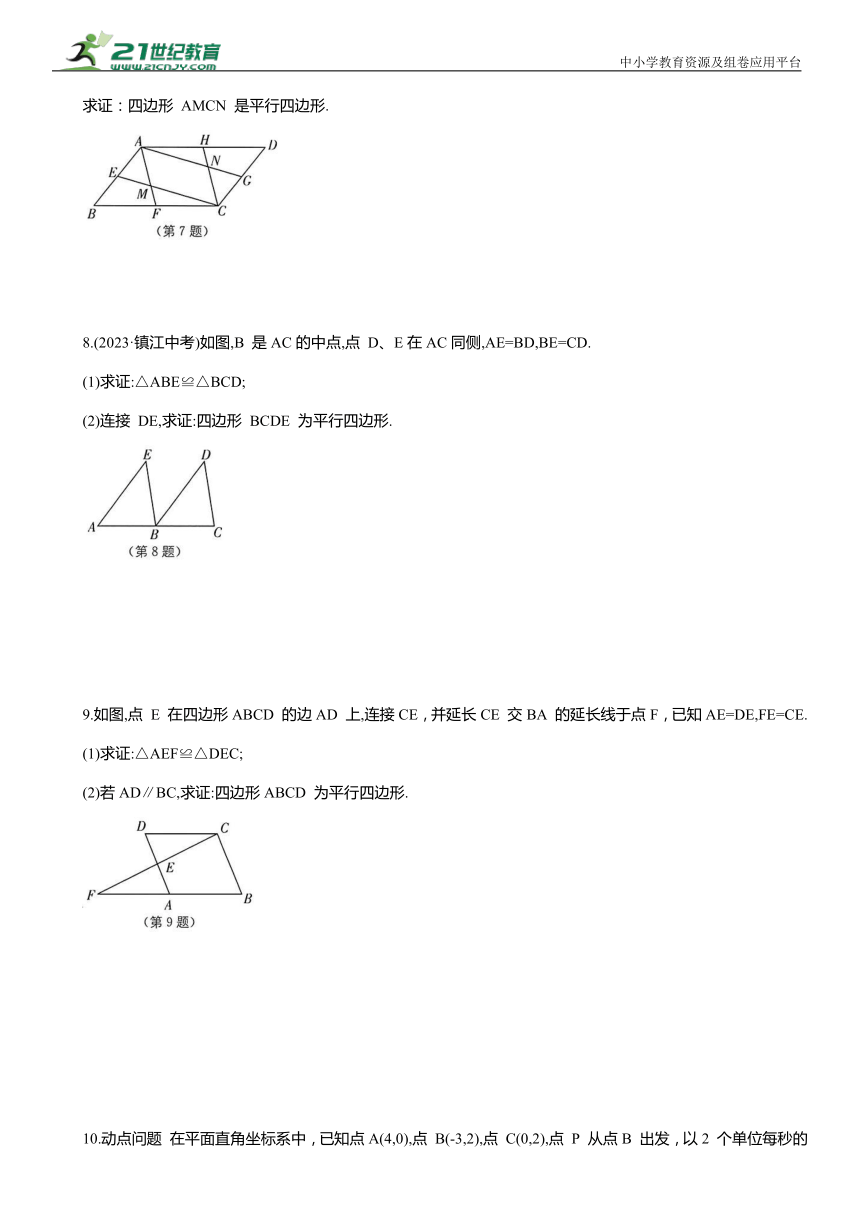
求证:四边形 AMCN 是平行四边形.
8.(2023·镇江中考)如图,B 是AC的中点,点 D、E在AC同侧,AE=BD,BE=CD.
(1)求证:△ABE≌△BCD;
(2)连接 DE,求证:四边形 BCDE 为平行四边形.
9.如图,点 E 在四边形ABCD 的边AD 上,连接CE,并延长CE 交BA 的延长线于点F,已知AE=DE,FE=CE.
(1)求证:△AEF≌△DEC;
(2)若AD∥BC,求证:四边形ABCD 为平行四边形.
10.动点问题 在平面直角坐标系中,已知点A(4,0),点 B(-3,2),点 C(0,2),点 P 从点B 出发,以2 个单位每秒的速度沿射线BC 运动,点Q 从点A 出发,开始以1个单位每秒的速度向原点O运动,到达原点后立刻以原来3倍的速度沿射线OA 运动,若P、Q两点同时出发,设运动时间为t秒,则当t= 时,以点 A、Q、C、P 为顶点的四边形为平行四边形.
11.如图,点E 在BC 上,△ABC≌△EAD.
(1)求证:四边形ABCD 是平行四边形;
(2)若AE 平分∠DAB,∠EDC=30°,求∠AED的度数.
12.(2024·武汉中考)如图,在□ABCD 中,点 E、F分别在边BC、AD上,AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接EF.请添加一个与线段相关的条件,使四边形 ABEF 是平行四边形.(不需要说明理由)
第3课时 平行四边形(3)
1.(2023·衡阳中考)如图,在四边形ABCD 中,已知AD∥BC.添加下列条件不能判定四边形 AB-CD 是平行四边形的是( ).
A. AD=BC B. AB∥DC
C. AB=DC D. ∠A=∠C
2.(2024·苏州期末)如图,在四边形 ABCD 中,AD∥BC,AD=BC,点 E、F 在对角线 BD 上,连接AE、AF、CE、CF,则添加下列条件,仍不能判断四边形 AECF 是平行四边形的是( ).
A. BE=DF B. ∠AEB=∠CFD
C. AE=CF D. AE⊥BD,CF⊥BD
3.在四边形 ABCD 中,现给出下列结论:
①若四边形 ABCD 是平行四边形,则AC=BD;
②若AB∥CD,∠A=∠C,则四边形ABCD是平行四边形;
③若AB=CD,∠A=∠C,则四边形ABCD是平行四边形;
④若四边形 ABCD 是平行四边形,则平行四边形 ABCD 的面积最大值是 AC·BD.
其中正确的结论是 .(写出所有正确结论的序号)
4. 如图,在 ABCD 中,点 E、F 分别在边AB、CD 上,∠ADE=∠CBF,EF 与BD 相交于点O.求证:BO=DO.
5. (2024·泸州中考)如图,在 ABCD中,E、F 是对角线 BD 上的点,且DE=BF.求证:∠1=∠2.
6. 如图,在 ABCD中,AB=8,点 E 是AB 上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点 F,则BF 的长为( ).
A. 5 B. 4 C. 3 D. 2
7.(2023·聊城中考)如图,在 ABCD 中,BC 的垂直平分线EO交AD 于点E,交 BC于点O,连接BE、CE,过点C作CF∥BE,交EO的延长线于点 F,连接BF.若AD=8,CE=5,则四边形 BFCE 的面积为 .
8. 定义:作 ABCD 的一组邻角的平分线,设交点为 P,点P 与这组邻角的公共边组成的三角形为□ABCD 的“伴侣三角形”.△PBC 为平行四边形ABCD 的伴侣三角形,AB=m,BC=4,连接AP 并延长交直线CD 于点 Q,若点 Q 落在线段CD 上(包括端点C、D),则m 的取值范围为 .
9.(2024·宿迁宿豫区三模)如图, ABCD 的对角线AC、BD 交于点O,在OA、OC 的延长线上分别取E、F 两点,使∠ABE=∠CDF.求证:
(1)△ABE≌△CDF;
(2)四边形 BEDF 是平行四边形.
10.如图,在四边形ABCD中,AC、BD 相交于点O,点O是AC的中点,AD∥BC,AC=8,BD=6.
(1)求证:四边形 ABCD 是平行四边形;
(2)若AC⊥BD,求 ABCD的面积.
11. 如图,在平行四边形 ABCD 中,点 E、F 分别是边AD、BC 的中点,分别连接CE、AF 交对角线BD于点G、H,连接EH、FG.
(1)求证:△ABF≌△CDE;
(2)求证:四边形EHFG 是平行四边形.
12.如图,在平行四边形 ABCD 中,∠DAC=60°,点E是BC边上一点,连接AE,AE=AB,点F是对角线AC边上一动点,连接EF.
(1)如图(1),若点 F 与对角线交点O重合,已知BE=4,OC:EC=5:3,求 AC的长度;
(2)如图(2),若EC=FC,点G是AC边上一点,连接BG、EG,已知∠AEG=60°,∠AGB+∠BCD=180°,求证:BG+EG=DC.
13. [问题]如图,在□ABCD中,AB=8,AD=5,∠DAB、∠ABC 的平分线AE、BF 分别与直线CD 交于点 E、F,求EF 的长.
[答案]EF=2.
[探究](1)把“问题”中的条件“AB=8”去掉,其余条件不变.
①当点 E 与点 F 重合时,求 AB 的长;
②当点 E 与点C 重合时,求 EF 的长.
(2)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当点C、D、E、F相邻两点间的距离相等时,求 的值.
14.(2024·浙江中考)尺规作图问题:如图(1),点 E 是□ABCD边 AD 上一点(不包含 A、D),连接CE.用尺规作AF∥CE,F是边 BC 上一点.
小明:如图(2).以C 为圆心,AE 长为半径作弧,交BC 于点 F,连接AF,则AF∥CE.
小丽:以点 A 为圆心,CE 长为半径作弧,交BC 于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明:AF∥CE;
(2)指出小丽作法中存在的问题.
9.3 平行四边形
第1课时 平行四边形(1)
1. D [解析]∵四边形ABCD 是平行四边形,
∴AD∥BC,∠B=∠D=58°,∴∠DAE=∠BEA.
∵AE 平分∠BAD 且交BC 于点E,
∴∠DAE=∠BAE,
故选D.
2. B [解析]∵四边形ABCD 是平行四边形,
∴∠B=∠D,∠A+∠B=180°.
∵∠B+∠D=100°,∴∠B=∠D=50°,
∴∠A=130°.故选 B.
3. A [解析]∵四边形 ABCD 是平行四边形,AC=10cm,BD=6cm,
4(cm).∴BC=AD=4cm.故选 A.
方法诠释 本题考查了平行四边形的性质:平行四边形的对角线互相平分,解题时还要注意勾股定理的应用.
4. C [解析]∵四边形ABCD 是平行四边形,AD=8cm,AB=5cm,
∴AD=BC=8cm,AB=CD=5cm,AD∥BC,
∴∠ADE=∠DEC.
∵DE 平分∠ADC,∴∠ADE=∠EDC,
∴∠EDC=∠DEC,∴CE=DC=5cm,
∴BE=BC-CE=3cm.故选C.
方法诠释本题主要考查平行四边形的性质、等腰三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.
5. B [解析]∵四边形ABCD 是平行四边形,AC=10,BD=6,∴OA=OC=5,OD=OB=3.
在△OAB 中,OA-OB∴5-36.26° [解析]∵四边形ABCD 是平行四边形,
∴∠ABC=∠D=102°,AD=BC.
∵AD=AE=BE,∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB.
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,∴∠CAB+∠ACB=3∠CAB=
7. D [解析]设D(x,y),
∵□ABCD的顶点坐标分别是A(0,1)、B(a,b)、C(3,-2),
∴D(-a+3,-b-1).故选 D.
知识拓展 平行四边形的性质有:平行四边形对边平行且相等;平行四边形对角相等,邻角互补;平行四边形对角线互相平分;平行四边形是中心对称图形,对称中心是两条对角线的交点等.
8. C [解析]∵四边形ABCD 是平行四边形,∴AB∥CD,∠1=∠EBA.
由折叠的性质,得∠EBD=∠ABD,
∴∠A=180°-∠2-∠ABD=180°-42°-28°=110°.故选C.
9.115° [解析]在四边形 BCDE 中,∠E=65°,∠EBC=
∵四边形ABCD 是平行四边形,∴∠A=∠C=115°.
10.(1,-1) [解析]如图,连接BD,设AD与y轴交于点M,
∵点A 的横坐标为4,AD 平行于x轴,且 AD 长为5.∴点D 的横坐标为-1.
∵平行四边形 ABCD 的面积为10, ∴点 D(-1,1).
∵四边形ABCD 是平行四边形,
∴BO=DO,∴点B(1,-1).
11.∵四边形 ABCD 是平行四边形,
∴AB=CD,AB∥CD,∴∠B=∠DCF,在△ABE与△DCF 中
∴△ABE≌△DCF(SAS).
12.∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC.∴∠EAO=∠FCO.
∵DE=BF,∴AE=CF.
在△AOE 和△COF 中
∴△AOE ≌△COF(AAS).∴OE=OF.
13.∵四边形ABCD 是平行四边形,
∴AD=BC,BD=2BO.
由已知BD=2AD,∴BO=BC.
又E是OC中点,∴BE⊥AC.
14.∵四边形ABCD 是平行四边形,
∴AB=CD,∠B=∠D,∠BAD=∠BCD.
∵AE平分∠BAD,交 BC 于点 E,CF 平分∠BCD,交AD于点F,∴∠BAE=∠FCD.
∴△ABE≌△CDF(ASA),∴AE=CF.
15.(1)∵四边形 ABCD 是平行四边形,∴AB=CD,BC=AD,∠B=∠D,AD∥BC.∴AF∥EC.
∵EA⊥AC,FC⊥AC,∴EA∥FC.
∴四边形 AECF 是平行四边形.
∴EC=AF.∴BE=BC-EC=AD-AF=DF.
在△ABE 和△CDF 中
∴△ABE ≌△CDF(SAS).
(2)如图,过点 A 作AG⊥EC于点G.
∵EA⊥AC,∠AEC=45°,
∴△AEC 为等腰直角三角形.
第2课时 平行四边形(2)
1. D [解析]A.根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;B.根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;C.根据平行四边形的判定定理:对角线互相平分的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;D.一组对边平行,另一组对边相等,可能是等腰梯形,故不能判断这个四边形是平行四边形,符合题意.故选 D.
2. C [解析]∵四边形ABCD 是平行四边形,
∵DE∥AC,CE∥BD,
∴四边形OCED 是平行四边形,
∴四边形OCED 的周长=2(OC+OD)=8.故选C.
3. DO=BO(答案不唯一)
4.如图,连接AC,交BD 于点O,
∵四边形ABCD 是平行四边形,
∴AO=CO,BO=DO.
∵DE=BF,∴BO-BF=DO-DE,即FO=EO,
∴四边形AECF 是平行四边形.
5. D
6. ①②④ [解析]①∵BD∥CF,DE∥BC,
∴四边形 BCFD 为平行四边形,故选项①符合题意;②∵DF∥BC,DF=BC,∴四边形 BCFD为平行四边形,故选项②符合题意;
③由DF∥BC,BD=CF,不能判定四边形 BCFD为平行四边形,故选项③不符合题意;
④∵DE∥BC,∴∠B+∠BDF=180°.
∵∠B=∠F,∴∠F+∠BDF=180°,
∴BD∥CF,∴四边形 BCFD 为平行四边形,故选项
④符合题意.综上所述,能使四边形 BCFD 是平行四边形的是①②④.
7.∵点E、F、G、H 分别是平行四边形ABCD 各边的中点,∴AH∥CF,AH=CF,
∴四边形AFCH 是平行四边形,∴AM∥CN.
同理可得,四边形AECG 是平行四边形,
∴AN∥CM,∴四边形AMCN 是平行四边形.
8.(1)∵B 是AC的中点,∴AB=BC,
在△ABE与△BCD 中
∴△ABE≌△BCD(SSS).
(2)∵△ABE≌△BCD,∴∠ABE=∠BCD,
∴BE∥CD.又BE=CD,
∴四边形 BCDE 为平行四边形.
方法诠释 本题考查了全等三角形的判定和性质以及平行四边形的判定,熟练掌握全等三角形的判定和性质定理是解题的关键.
9.(1)在△AEF 和△DEC中.
∴△AEF≌△DEC(SAS).
(2)∵△AEF≌△DEC,∴∠AFE=∠DCE,
∴AB∥CD.又AD∥BC,
∴四边形ABCD 为平行四边形.
10.1或3或13 [解析]∵A(4,0)、B(--3,2)、C(0, 2),∴OA=4,BC=3,BC∥x轴.
∵PC∥AQ,∴当 PC=AQ 时,以点 A、Q、C、P为顶点的四边形为平行四边形.
若 时,BP=2t,PC=3-2t,AQ=t,此时3-2t=t,解得t=1;
若 时,BP=2t,PC=2t-3,AQ=t,此时2t-3=t,解得t=3;
若 时,BP=2t,PC=2t-3,OQ=3(t-4),AQ=4-3(t-4),此时2t-3=4-3(t-4),解得 (舍去);
若 时,BP=2t,PC=2t--3,OQ=3(t-4),AQ=3(t-4)-4,此时2t-3=3(t-4)-4,解得t=13.综上所述,当t为1或3或13秒时,以点A、Q、C、P为顶点的四边形为平行四边形.
11.(1)∵△ABC≌△EAD,
∴BC=AD,∠B=∠EAD,AB=EA,
∴∠B=∠AEB,∴∠EAD=∠AEB,
∴BC∥AD,∴四边形ABCD是平行四边形.
(2)由(1),得∠B=∠AEB=∠EAD,四边形 ABCD是平行四边形,∴∠ADC=∠B.
∵AE平分∠DAB,∴∠BAE=∠EAD,
∴∠B=∠AEB=∠BAE,
∴△ABE 是等边三角形,
∴∠ADC=∠B=∠BAE=∠EAD=60°,
∴∠ADE=∠ADC-∠EDC=60°-30°=30°,
12.(1)∵四边形 ABCD 是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
∵AF=CE,∴AD-AF=BC-CE,∴DF=BE.
在△ABE 与△CDF 中
∴△ABE≌△CDF(SAS).
(2)添加BE=CE,理由如下:
∵AF=CE,BE=CE,∴AF=BE.
∵四边形ABCD 是平行四边形,∴AD∥BC,
∴四边形ABEF 是平行四边形.
方法诠释 本题主要考查了三角形全等的判定,证明三角形全等的几种方法:①SAS;②ASA;③AAS;④SSS;⑤HL.
第3课时 平行四边形(3)
1. C [解析]A.因为AD∥BC,AD=BC,因此由一组对边平行且相等的四边形是平行四边形,能判定四边形ABCD 是平行四边形,故A 不符合题意;
B.因为AD∥BC,AB∥DC,因此由两组对边分别平行的四边形是平行四边形,能判定四边形 ABCD 是平行四边形,故B不符合题意;
C. AB=DC,但AB 和CD不一定平行,因此不能判定四边形ABCD 是平行四边形,故C符合题意;
D.因为 AD∥BC 得到∠ADB=∠CBD.又∠A=∠C,BD=DB,因此△ABD≌△CDB(AAS),得到AD=CB,能判定四边形ABCD 是平行四边形,故D不符合题意.故选 C.
2. C [解析]∵AD∥BC,AD=BC,
∴四边形ABCD 是平行四边形.
A.如图,连接AC,交 BD于点O,
∵四边形ABCD 是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF,∴BO--BE=DO--DF,∴EO=FO,
∴四边形AECF 为平行四边形,故选项 A不符合题意;
B.∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵∠AEB=∠CFD,∴∠AEF=∠CFE,
∴AE∥CF.
在△ABE 和△CDF 中,
∴△ABE≌△CDF(AAS),∴AE=CF,又AE∥CF,∴四边形AECF 为平行四边形,故选项B不符合题意;
C.由AE=CF,不能证明△ABE≌△CDF,不能使四边形AECF 为平行四边形,故选项C符合题意;
D.∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF.
∴△ABE≌△CDF(AAS),∴AE=CF,
∴四边形AECF 为平行四边形,故选项D不符合题意.故选 C.
3.②④ [解析]①若四边形 ABCD 是平行四边形,则AC、BD 互相平分但不一定相等,故①错误;②若AB∥CD,∠A=∠C,则四边形 ABCD 是平行四边形,故②正确;③若AB=CD,∠A=∠C,则四边形ABCD 不一定是平行四边形,故③错误;④若四边形ABCD 是平行四边形,则当 AC⊥BD 时平行四边形ABCD 的面积最大,最大值是 AC·BD.故④正确.故正确的结论为②④.
4.∵四边形ABCD 是平行四边形,
∴AB=CD,AD=BC,∠A=∠C.
在△DAE 和△BCF 中
∴△DAE ≌△BCF(ASA),
∴DE=BF,AE=CF.
∵AB=CD,∴BE=DF,
∴四边形 BFDE 是平行四边形,∴OB=OD.
5.∵四边形ABCD 是平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF.
在△ADE 和△CBF 中
∴△ADE≌△CBF(SAS),∴∠1=∠2.
6. C [解析]在 ABCD中,AB=8,
∴CD=AB=8,AB∥CD.
∵AE=3,∴BE=AB-AE=5.
又CF∥DE,∴四边形DEFC是平行四边形,
∴EF=DC=8,∴BF=EF--BE=8-5=3.故选 C.
归纳总结 本题考查了平行四边形的性质以及判定,能够熟练运用平行四边形的判定是解题的关键,平行四边形的判定包括:(1)两组对边分别平行的四边形是平行四边形(定义判定法);(2)一组对边平行且相等的四边形是平行四边形;(3)两组对边分别相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形(两组对边平行判定);(5)对角线互相平分的四边形是平行四边形.
7.24 [解析]∵四边形 ABCD 是平行四边形,AD=8,∴AD=BC=8.∵EF 是线段BC 的垂直平分线,
∵CF∥BE,∴∠OCF=∠OBE.在△OCF 与△OBE 中
∴△OCF≌△OBE(ASA),∴OE=OF=3,
解后反思 本题考查的是平行四边形的性质、三角形的面积及线段垂直平分线的性质,根据题意得出OE=OF 是解题的关键.
8.2≤m≤4 [解析]在平行四边形ABCD 中,∠ABC+∠BCD=180°,
∵BP 平分∠ABC,PC平分∠BCD,
∴∠BPC=90°.
当点 Q 与点C 重合时,如图(1)所示:
∵BP 平分∠ABC,∴∠ABP=∠CBP.
∵∠BPC=90°,∴∠APB=∠BPC=90°.
又BP=BP,∴△ABP≌△CBP(ASA),
∴AB=BC.∵BC=4,∴m=4.
当点 Q 与点D 重合时,如图(2)所示:
延长CP 交BA 的延长线于点K,∵BP 平分∠ABC,∴∠ABP=∠CBP.
∵∠BPC=90°,∴∠KPB=∠BPC=90°.
又BP=BP,∴△KBP≌△CBP(ASA),
∴BK=BC,KP=CP.
∵AB∥CD,∴∠K=∠DCP.
又∠KPA=∠CPD,∴△KPA≌△CPD(ASA),
∴CD=AK.∵AB=CD,∴BC=2AB=4,
∴AB=2,∴m=2.
综上所述,当点Q落在线段CD上时,m的取值范围是2≤m≤4.
9.(1)∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD,∴∠BAC=∠DCA,
∴∠BAE=∠DCF.又∠ABE=∠CDF,
∴△ABE≌△CDF(ASA).
(2)∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD.
由(1)可知,△ABE≌△CDF,∴AE=CF,∴OA+AE=OC+CF,即OE=OF,又OB=OD,∴四边形BEDF 是平行四边形.
10.(1)∵O是AC的中点,∴OA=OC.
∵AD∥BC,∴∠ADO=∠CBO.
在△AOD 和△COB 中
∴△AOD ≌△COB(AAS).∴OD=OB.
∴四边形ABCD 是平行四边形.
(2)∵四边形ABCD 是平行四边形,AC⊥BD,∴□ABCD的面积:
11.(1)∵点E、F 分别是边AD、BC的中点,
∵四边形ABCD 是平行四边形,
∴AD=CB,AB=CD,∠ABF=∠CDE,
∴DE=BF.
在△ABF 和△CDE 中 ∴△ABF≌△CDE(SAS).
(2)∵BC∥AD,∴∠FBH=∠EDG.
∵△ABF≌△CDE,∴∠BFH=∠DEG.
在△BFH 和△DEG中,
∴△BFH≌△DEG(ASA),∴FH=EG.
∵CF∥AE,CF=AE,
∴四边形 AECF 是平行四边形,∴AF∥CE,
∴FH∥EG,又FH=EG,
∴四边形EHFG 是平行四边形.
12.(1)过点 A 作AH⊥BE于点 H,如图(1),
∵OC:EC=5:3,
不妨设OC=5x,则EC=3x,AC=10x,
∴CH=CE+EH=3x+2.
∵四边形 ABCD 是平行四边形,
∴AD∥BC,∴∠ACH=∠DAC=60°,
∴10x=2(3x+2),解得x=1.∴AC=10.
(2)延长EG 至点M,使得 EM=AE,连接AM,如图(2),
∵∠AEG=60°,∴△AEM 为等边三角形,
∴AE=AM,∠M=60°.
∵AB=AE,∴∠ABE=∠AEB,AB=AM.
∵四边形ABCD 是平行四边形,
∴AB∥CD. ∴∠ABC+∠BCD=180°.
∵∠AGB+∠BCD=180°,∴∠ABC=∠AGB.
∵∠AEG=∠ACB=60°,
∴∠AEB+∠CEG=∠CEG+∠CGE=120°,
∴∠AEB=∠CGE.
∵∠AGB=∠ABE=∠AEB,∠AGM=∠CGE,
∴∠AGB=∠AGM.
又AG=AG,∴△ABG≌△AMG(AAS).
∴BG=MG,∴BG+EG=MG+EG=EM.
∵AE=EM,∴AE=BG+EG.
∵四边形ABCD 是平行四边形,∴AB=DC.
∵AB=AE,∴BG+EG=DC.
13.(1)①如图(1),∵四边形 ABCD 是平行四边形,
∴AB∥CD.∴∠DEA=∠EAB.
∵AE 平分∠DAB,∴∠DAE=∠EAB.
∴∠DAE=∠DEA. ∴DE=AD=5.
同理可得BC=CF=5.
∵点E与点F 重合,∴AB=CD=10.
②当点E 与点C重合时,同理可证DE=DC=AD=5.
∵CF=BC=5,∴点 F 与点D 重合.
∴EF=DC=5.
(2)分三种情况讨论:
如图(2),易知AD=DE=EF=CF,∴AD=
如图(3),易知AD=DE,BC=CF.
又
如图(4),∵AD=DE,CB=CF,又
综上所述, 的值为 、 或2.
素养考向 动点问题:所谓“动点问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.
14.(1)根据小明的作法,知CF=AE,
∵四边形ABCD 是平行四边形,∴AD∥BC.
又CF=AE,∴四边形AFCE 是平行四边形,
∴AF∥CE.
(2)以A 为圆心,EC 为半径画弧,交 BC 于点F,此时会有两个交点,只有其中之一符合题意.故小丽的作法有问题.
第 1课时 平行四边形(1)
1.如图,在平行四边形 ABCD中,AE 平分∠BAD 且交 BC 于点 E,∠D=58°,则∠AEC 的度数是( ).
A. 61°B. 109°C. 112°D. 119°
2.(2024·无锡宜兴模拟)在平行四边形 ABCD 中,∠B+∠D=100°,则∠A 等于( ).
A. 50°B. 130°C. 100°D. 65°
3.如图,在平行四边形 ABCD 中,AC、BD 相交于点 O,∠ODA = 90°,AC =10 cm,BD =6cm,则 BC 的长为( ).
A. 4 cm B. 5cm C. 6 cm D. 8cm
4.(2024·苏州姑苏区期中)如图,在□ABCD 中,已知AD=8cm,AB=5cm ,DE 平分∠ADC 交BC 边于点E,则 BE 等于( ).
A. 1cm B. 2cm C. 3cm D. 4cm
5. 在 ABCD中,对角线AC 和 BD 相交于点 O,如果AC=10,BD=6,AB=m,那么m的取值范围是( ).
A. 1
7.如图,在平面直角坐标系中,□ABCD 的顶点坐标分别是A(0,1)、B(a,b)、C(3,-2),则D的坐标是( ).
A. (-a+3,-b+1)
B. (-a--3,-b--1)
C. (-a-3,-b+1)
D. (-a+3,-b--1)
8.如图,将平行四边形 ABCD 沿对角线BD 折叠,使点 A 落在点 E 处.若∠1=56°,∠2=42°,则∠A 的度数为( ).
A. 108° B. 109°
C. 110° D. 111°
9.如图,点 E 为 ABCD外一点,且EB⊥BC,ED⊥CD,若∠E=65°,则∠A 的度数为 .
10.如图,已知坐标原点O 为平行四边形ABCD的对角线AC 的中点,顶点 A 的横坐标为4,AD 平行于x轴,且AD 长为5.若平行四边形面积为10,则顶点 B 的坐标为 .
11. (2024·淮安淮安区期末)如图,在 ABCD 中,点E在边BC上,点 F 在BC 的延长线上,且 BE=CF.求证:△ABE≌△DCF.
12.如图,在 ABCD 中,点 E、F 分别在AD、BC上,且DE=BF,连接EF 交AC 于点O.求证:OE=OF.
13.已知:平行四边形ABCD中,对角线AC、BD 相交于点O,BD=2AD,E、F、G分别是OC、OD、AB 的中点.求证:BE⊥AC.
14. 如图,在□ABCD 中,AE 平分∠BAD,交 BC 于点 E,CF 平分∠BCD,交AD 于点 F.求证:AE=CF.
15.如图,在平行四边形 ABCD 中,点 E、F 分别在边BC、AD上,EA⊥AC,FC⊥AC.
(1)求证:△ABE≌△CDF;
(2)若∠B=30°,∠AEC=45°,求证:AB=AF.
中小学教育资源及组卷应用平台
第2课时 平行四边形(2)
1.(2024·乐山中考)如图,下列条件中不能判定四边形 ABCD 为平行四边形的是( ).
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
2.(2024·辽宁中考)如图,□ABCD 的对角线AC、BD 相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED 的周长为( ).
A. 4 B. 6 C. 8 D. 16
3.中考新考法 满足结论的条件开放 (2024·镇江丹阳期中)如图,在四边形 ABCD 中,AC 与 BD 相交于点O,AO=CO,添加条件 ,可得四边形 ABCD 为平行四边形(只需添加一个条件).
4. 教材P69例3·变式(2024·苏州姑苏区期末)如图,点E、F 是□ABCD 对角线上两点,且 DE=BF,连接AE、AF、CE、CF.求证:四边形 AECF为平行四边形.
5.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( ).
A. ①② B. ①④
C. ③④ D. ②③
6.如图,在△ABC 中,点 D、E 分别是AB、AC 上的点,且DE∥BC,点 F 是 DE 延长线上一点,连接CF.添加下列条件:①BD∥CF;②DF=BC;③BD=CF;④∠B=∠F.能使四边形BCFD 是平行四边形的是 (填上所有符合要求的条件的序号).
7.如图,点 E、F、G、H 分别是平行四边形ABCD 各边的中点,连接AF、CE相交于点M,连接AG、CH 相交于点N.
求证:四边形 AMCN 是平行四边形.
8.(2023·镇江中考)如图,B 是AC的中点,点 D、E在AC同侧,AE=BD,BE=CD.
(1)求证:△ABE≌△BCD;
(2)连接 DE,求证:四边形 BCDE 为平行四边形.
9.如图,点 E 在四边形ABCD 的边AD 上,连接CE,并延长CE 交BA 的延长线于点F,已知AE=DE,FE=CE.
(1)求证:△AEF≌△DEC;
(2)若AD∥BC,求证:四边形ABCD 为平行四边形.
10.动点问题 在平面直角坐标系中,已知点A(4,0),点 B(-3,2),点 C(0,2),点 P 从点B 出发,以2 个单位每秒的速度沿射线BC 运动,点Q 从点A 出发,开始以1个单位每秒的速度向原点O运动,到达原点后立刻以原来3倍的速度沿射线OA 运动,若P、Q两点同时出发,设运动时间为t秒,则当t= 时,以点 A、Q、C、P 为顶点的四边形为平行四边形.
11.如图,点E 在BC 上,△ABC≌△EAD.
(1)求证:四边形ABCD 是平行四边形;
(2)若AE 平分∠DAB,∠EDC=30°,求∠AED的度数.
12.(2024·武汉中考)如图,在□ABCD 中,点 E、F分别在边BC、AD上,AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接EF.请添加一个与线段相关的条件,使四边形 ABEF 是平行四边形.(不需要说明理由)
第3课时 平行四边形(3)
1.(2023·衡阳中考)如图,在四边形ABCD 中,已知AD∥BC.添加下列条件不能判定四边形 AB-CD 是平行四边形的是( ).
A. AD=BC B. AB∥DC
C. AB=DC D. ∠A=∠C
2.(2024·苏州期末)如图,在四边形 ABCD 中,AD∥BC,AD=BC,点 E、F 在对角线 BD 上,连接AE、AF、CE、CF,则添加下列条件,仍不能判断四边形 AECF 是平行四边形的是( ).
A. BE=DF B. ∠AEB=∠CFD
C. AE=CF D. AE⊥BD,CF⊥BD
3.在四边形 ABCD 中,现给出下列结论:
①若四边形 ABCD 是平行四边形,则AC=BD;
②若AB∥CD,∠A=∠C,则四边形ABCD是平行四边形;
③若AB=CD,∠A=∠C,则四边形ABCD是平行四边形;
④若四边形 ABCD 是平行四边形,则平行四边形 ABCD 的面积最大值是 AC·BD.
其中正确的结论是 .(写出所有正确结论的序号)
4. 如图,在 ABCD 中,点 E、F 分别在边AB、CD 上,∠ADE=∠CBF,EF 与BD 相交于点O.求证:BO=DO.
5. (2024·泸州中考)如图,在 ABCD中,E、F 是对角线 BD 上的点,且DE=BF.求证:∠1=∠2.
6. 如图,在 ABCD中,AB=8,点 E 是AB 上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点 F,则BF 的长为( ).
A. 5 B. 4 C. 3 D. 2
7.(2023·聊城中考)如图,在 ABCD 中,BC 的垂直平分线EO交AD 于点E,交 BC于点O,连接BE、CE,过点C作CF∥BE,交EO的延长线于点 F,连接BF.若AD=8,CE=5,则四边形 BFCE 的面积为 .
8. 定义:作 ABCD 的一组邻角的平分线,设交点为 P,点P 与这组邻角的公共边组成的三角形为□ABCD 的“伴侣三角形”.△PBC 为平行四边形ABCD 的伴侣三角形,AB=m,BC=4,连接AP 并延长交直线CD 于点 Q,若点 Q 落在线段CD 上(包括端点C、D),则m 的取值范围为 .
9.(2024·宿迁宿豫区三模)如图, ABCD 的对角线AC、BD 交于点O,在OA、OC 的延长线上分别取E、F 两点,使∠ABE=∠CDF.求证:
(1)△ABE≌△CDF;
(2)四边形 BEDF 是平行四边形.
10.如图,在四边形ABCD中,AC、BD 相交于点O,点O是AC的中点,AD∥BC,AC=8,BD=6.
(1)求证:四边形 ABCD 是平行四边形;
(2)若AC⊥BD,求 ABCD的面积.
11. 如图,在平行四边形 ABCD 中,点 E、F 分别是边AD、BC 的中点,分别连接CE、AF 交对角线BD于点G、H,连接EH、FG.
(1)求证:△ABF≌△CDE;
(2)求证:四边形EHFG 是平行四边形.
12.如图,在平行四边形 ABCD 中,∠DAC=60°,点E是BC边上一点,连接AE,AE=AB,点F是对角线AC边上一动点,连接EF.
(1)如图(1),若点 F 与对角线交点O重合,已知BE=4,OC:EC=5:3,求 AC的长度;
(2)如图(2),若EC=FC,点G是AC边上一点,连接BG、EG,已知∠AEG=60°,∠AGB+∠BCD=180°,求证:BG+EG=DC.
13. [问题]如图,在□ABCD中,AB=8,AD=5,∠DAB、∠ABC 的平分线AE、BF 分别与直线CD 交于点 E、F,求EF 的长.
[答案]EF=2.
[探究](1)把“问题”中的条件“AB=8”去掉,其余条件不变.
①当点 E 与点 F 重合时,求 AB 的长;
②当点 E 与点C 重合时,求 EF 的长.
(2)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当点C、D、E、F相邻两点间的距离相等时,求 的值.
14.(2024·浙江中考)尺规作图问题:如图(1),点 E 是□ABCD边 AD 上一点(不包含 A、D),连接CE.用尺规作AF∥CE,F是边 BC 上一点.
小明:如图(2).以C 为圆心,AE 长为半径作弧,交BC 于点 F,连接AF,则AF∥CE.
小丽:以点 A 为圆心,CE 长为半径作弧,交BC 于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明:AF∥CE;
(2)指出小丽作法中存在的问题.
9.3 平行四边形
第1课时 平行四边形(1)
1. D [解析]∵四边形ABCD 是平行四边形,
∴AD∥BC,∠B=∠D=58°,∴∠DAE=∠BEA.
∵AE 平分∠BAD 且交BC 于点E,
∴∠DAE=∠BAE,
故选D.
2. B [解析]∵四边形ABCD 是平行四边形,
∴∠B=∠D,∠A+∠B=180°.
∵∠B+∠D=100°,∴∠B=∠D=50°,
∴∠A=130°.故选 B.
3. A [解析]∵四边形 ABCD 是平行四边形,AC=10cm,BD=6cm,
4(cm).∴BC=AD=4cm.故选 A.
方法诠释 本题考查了平行四边形的性质:平行四边形的对角线互相平分,解题时还要注意勾股定理的应用.
4. C [解析]∵四边形ABCD 是平行四边形,AD=8cm,AB=5cm,
∴AD=BC=8cm,AB=CD=5cm,AD∥BC,
∴∠ADE=∠DEC.
∵DE 平分∠ADC,∴∠ADE=∠EDC,
∴∠EDC=∠DEC,∴CE=DC=5cm,
∴BE=BC-CE=3cm.故选C.
方法诠释本题主要考查平行四边形的性质、等腰三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.
5. B [解析]∵四边形ABCD 是平行四边形,AC=10,BD=6,∴OA=OC=5,OD=OB=3.
在△OAB 中,OA-OB
∴∠ABC=∠D=102°,AD=BC.
∵AD=AE=BE,∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB.
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,∴∠CAB+∠ACB=3∠CAB=
7. D [解析]设D(x,y),
∵□ABCD的顶点坐标分别是A(0,1)、B(a,b)、C(3,-2),
∴D(-a+3,-b-1).故选 D.
知识拓展 平行四边形的性质有:平行四边形对边平行且相等;平行四边形对角相等,邻角互补;平行四边形对角线互相平分;平行四边形是中心对称图形,对称中心是两条对角线的交点等.
8. C [解析]∵四边形ABCD 是平行四边形,∴AB∥CD,∠1=∠EBA.
由折叠的性质,得∠EBD=∠ABD,
∴∠A=180°-∠2-∠ABD=180°-42°-28°=110°.故选C.
9.115° [解析]在四边形 BCDE 中,∠E=65°,∠EBC=
∵四边形ABCD 是平行四边形,∴∠A=∠C=115°.
10.(1,-1) [解析]如图,连接BD,设AD与y轴交于点M,
∵点A 的横坐标为4,AD 平行于x轴,且 AD 长为5.∴点D 的横坐标为-1.
∵平行四边形 ABCD 的面积为10, ∴点 D(-1,1).
∵四边形ABCD 是平行四边形,
∴BO=DO,∴点B(1,-1).
11.∵四边形 ABCD 是平行四边形,
∴AB=CD,AB∥CD,∴∠B=∠DCF,在△ABE与△DCF 中
∴△ABE≌△DCF(SAS).
12.∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC.∴∠EAO=∠FCO.
∵DE=BF,∴AE=CF.
在△AOE 和△COF 中
∴△AOE ≌△COF(AAS).∴OE=OF.
13.∵四边形ABCD 是平行四边形,
∴AD=BC,BD=2BO.
由已知BD=2AD,∴BO=BC.
又E是OC中点,∴BE⊥AC.
14.∵四边形ABCD 是平行四边形,
∴AB=CD,∠B=∠D,∠BAD=∠BCD.
∵AE平分∠BAD,交 BC 于点 E,CF 平分∠BCD,交AD于点F,∴∠BAE=∠FCD.
∴△ABE≌△CDF(ASA),∴AE=CF.
15.(1)∵四边形 ABCD 是平行四边形,∴AB=CD,BC=AD,∠B=∠D,AD∥BC.∴AF∥EC.
∵EA⊥AC,FC⊥AC,∴EA∥FC.
∴四边形 AECF 是平行四边形.
∴EC=AF.∴BE=BC-EC=AD-AF=DF.
在△ABE 和△CDF 中
∴△ABE ≌△CDF(SAS).
(2)如图,过点 A 作AG⊥EC于点G.
∵EA⊥AC,∠AEC=45°,
∴△AEC 为等腰直角三角形.
第2课时 平行四边形(2)
1. D [解析]A.根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;B.根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;C.根据平行四边形的判定定理:对角线互相平分的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;D.一组对边平行,另一组对边相等,可能是等腰梯形,故不能判断这个四边形是平行四边形,符合题意.故选 D.
2. C [解析]∵四边形ABCD 是平行四边形,
∵DE∥AC,CE∥BD,
∴四边形OCED 是平行四边形,
∴四边形OCED 的周长=2(OC+OD)=8.故选C.
3. DO=BO(答案不唯一)
4.如图,连接AC,交BD 于点O,
∵四边形ABCD 是平行四边形,
∴AO=CO,BO=DO.
∵DE=BF,∴BO-BF=DO-DE,即FO=EO,
∴四边形AECF 是平行四边形.
5. D
6. ①②④ [解析]①∵BD∥CF,DE∥BC,
∴四边形 BCFD 为平行四边形,故选项①符合题意;②∵DF∥BC,DF=BC,∴四边形 BCFD为平行四边形,故选项②符合题意;
③由DF∥BC,BD=CF,不能判定四边形 BCFD为平行四边形,故选项③不符合题意;
④∵DE∥BC,∴∠B+∠BDF=180°.
∵∠B=∠F,∴∠F+∠BDF=180°,
∴BD∥CF,∴四边形 BCFD 为平行四边形,故选项
④符合题意.综上所述,能使四边形 BCFD 是平行四边形的是①②④.
7.∵点E、F、G、H 分别是平行四边形ABCD 各边的中点,∴AH∥CF,AH=CF,
∴四边形AFCH 是平行四边形,∴AM∥CN.
同理可得,四边形AECG 是平行四边形,
∴AN∥CM,∴四边形AMCN 是平行四边形.
8.(1)∵B 是AC的中点,∴AB=BC,
在△ABE与△BCD 中
∴△ABE≌△BCD(SSS).
(2)∵△ABE≌△BCD,∴∠ABE=∠BCD,
∴BE∥CD.又BE=CD,
∴四边形 BCDE 为平行四边形.
方法诠释 本题考查了全等三角形的判定和性质以及平行四边形的判定,熟练掌握全等三角形的判定和性质定理是解题的关键.
9.(1)在△AEF 和△DEC中.
∴△AEF≌△DEC(SAS).
(2)∵△AEF≌△DEC,∴∠AFE=∠DCE,
∴AB∥CD.又AD∥BC,
∴四边形ABCD 为平行四边形.
10.1或3或13 [解析]∵A(4,0)、B(--3,2)、C(0, 2),∴OA=4,BC=3,BC∥x轴.
∵PC∥AQ,∴当 PC=AQ 时,以点 A、Q、C、P为顶点的四边形为平行四边形.
若 时,BP=2t,PC=3-2t,AQ=t,此时3-2t=t,解得t=1;
若 时,BP=2t,PC=2t-3,AQ=t,此时2t-3=t,解得t=3;
若 时,BP=2t,PC=2t-3,OQ=3(t-4),AQ=4-3(t-4),此时2t-3=4-3(t-4),解得 (舍去);
若 时,BP=2t,PC=2t--3,OQ=3(t-4),AQ=3(t-4)-4,此时2t-3=3(t-4)-4,解得t=13.综上所述,当t为1或3或13秒时,以点A、Q、C、P为顶点的四边形为平行四边形.
11.(1)∵△ABC≌△EAD,
∴BC=AD,∠B=∠EAD,AB=EA,
∴∠B=∠AEB,∴∠EAD=∠AEB,
∴BC∥AD,∴四边形ABCD是平行四边形.
(2)由(1),得∠B=∠AEB=∠EAD,四边形 ABCD是平行四边形,∴∠ADC=∠B.
∵AE平分∠DAB,∴∠BAE=∠EAD,
∴∠B=∠AEB=∠BAE,
∴△ABE 是等边三角形,
∴∠ADC=∠B=∠BAE=∠EAD=60°,
∴∠ADE=∠ADC-∠EDC=60°-30°=30°,
12.(1)∵四边形 ABCD 是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
∵AF=CE,∴AD-AF=BC-CE,∴DF=BE.
在△ABE 与△CDF 中
∴△ABE≌△CDF(SAS).
(2)添加BE=CE,理由如下:
∵AF=CE,BE=CE,∴AF=BE.
∵四边形ABCD 是平行四边形,∴AD∥BC,
∴四边形ABEF 是平行四边形.
方法诠释 本题主要考查了三角形全等的判定,证明三角形全等的几种方法:①SAS;②ASA;③AAS;④SSS;⑤HL.
第3课时 平行四边形(3)
1. C [解析]A.因为AD∥BC,AD=BC,因此由一组对边平行且相等的四边形是平行四边形,能判定四边形ABCD 是平行四边形,故A 不符合题意;
B.因为AD∥BC,AB∥DC,因此由两组对边分别平行的四边形是平行四边形,能判定四边形 ABCD 是平行四边形,故B不符合题意;
C. AB=DC,但AB 和CD不一定平行,因此不能判定四边形ABCD 是平行四边形,故C符合题意;
D.因为 AD∥BC 得到∠ADB=∠CBD.又∠A=∠C,BD=DB,因此△ABD≌△CDB(AAS),得到AD=CB,能判定四边形ABCD 是平行四边形,故D不符合题意.故选 C.
2. C [解析]∵AD∥BC,AD=BC,
∴四边形ABCD 是平行四边形.
A.如图,连接AC,交 BD于点O,
∵四边形ABCD 是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF,∴BO--BE=DO--DF,∴EO=FO,
∴四边形AECF 为平行四边形,故选项 A不符合题意;
B.∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵∠AEB=∠CFD,∴∠AEF=∠CFE,
∴AE∥CF.
在△ABE 和△CDF 中,
∴△ABE≌△CDF(AAS),∴AE=CF,又AE∥CF,∴四边形AECF 为平行四边形,故选项B不符合题意;
C.由AE=CF,不能证明△ABE≌△CDF,不能使四边形AECF 为平行四边形,故选项C符合题意;
D.∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF.
∴△ABE≌△CDF(AAS),∴AE=CF,
∴四边形AECF 为平行四边形,故选项D不符合题意.故选 C.
3.②④ [解析]①若四边形 ABCD 是平行四边形,则AC、BD 互相平分但不一定相等,故①错误;②若AB∥CD,∠A=∠C,则四边形 ABCD 是平行四边形,故②正确;③若AB=CD,∠A=∠C,则四边形ABCD 不一定是平行四边形,故③错误;④若四边形ABCD 是平行四边形,则当 AC⊥BD 时平行四边形ABCD 的面积最大,最大值是 AC·BD.故④正确.故正确的结论为②④.
4.∵四边形ABCD 是平行四边形,
∴AB=CD,AD=BC,∠A=∠C.
在△DAE 和△BCF 中
∴△DAE ≌△BCF(ASA),
∴DE=BF,AE=CF.
∵AB=CD,∴BE=DF,
∴四边形 BFDE 是平行四边形,∴OB=OD.
5.∵四边形ABCD 是平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF.
在△ADE 和△CBF 中
∴△ADE≌△CBF(SAS),∴∠1=∠2.
6. C [解析]在 ABCD中,AB=8,
∴CD=AB=8,AB∥CD.
∵AE=3,∴BE=AB-AE=5.
又CF∥DE,∴四边形DEFC是平行四边形,
∴EF=DC=8,∴BF=EF--BE=8-5=3.故选 C.
归纳总结 本题考查了平行四边形的性质以及判定,能够熟练运用平行四边形的判定是解题的关键,平行四边形的判定包括:(1)两组对边分别平行的四边形是平行四边形(定义判定法);(2)一组对边平行且相等的四边形是平行四边形;(3)两组对边分别相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形(两组对边平行判定);(5)对角线互相平分的四边形是平行四边形.
7.24 [解析]∵四边形 ABCD 是平行四边形,AD=8,∴AD=BC=8.∵EF 是线段BC 的垂直平分线,
∵CF∥BE,∴∠OCF=∠OBE.在△OCF 与△OBE 中
∴△OCF≌△OBE(ASA),∴OE=OF=3,
解后反思 本题考查的是平行四边形的性质、三角形的面积及线段垂直平分线的性质,根据题意得出OE=OF 是解题的关键.
8.2≤m≤4 [解析]在平行四边形ABCD 中,∠ABC+∠BCD=180°,
∵BP 平分∠ABC,PC平分∠BCD,
∴∠BPC=90°.
当点 Q 与点C 重合时,如图(1)所示:
∵BP 平分∠ABC,∴∠ABP=∠CBP.
∵∠BPC=90°,∴∠APB=∠BPC=90°.
又BP=BP,∴△ABP≌△CBP(ASA),
∴AB=BC.∵BC=4,∴m=4.
当点 Q 与点D 重合时,如图(2)所示:
延长CP 交BA 的延长线于点K,∵BP 平分∠ABC,∴∠ABP=∠CBP.
∵∠BPC=90°,∴∠KPB=∠BPC=90°.
又BP=BP,∴△KBP≌△CBP(ASA),
∴BK=BC,KP=CP.
∵AB∥CD,∴∠K=∠DCP.
又∠KPA=∠CPD,∴△KPA≌△CPD(ASA),
∴CD=AK.∵AB=CD,∴BC=2AB=4,
∴AB=2,∴m=2.
综上所述,当点Q落在线段CD上时,m的取值范围是2≤m≤4.
9.(1)∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD,∴∠BAC=∠DCA,
∴∠BAE=∠DCF.又∠ABE=∠CDF,
∴△ABE≌△CDF(ASA).
(2)∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD.
由(1)可知,△ABE≌△CDF,∴AE=CF,∴OA+AE=OC+CF,即OE=OF,又OB=OD,∴四边形BEDF 是平行四边形.
10.(1)∵O是AC的中点,∴OA=OC.
∵AD∥BC,∴∠ADO=∠CBO.
在△AOD 和△COB 中
∴△AOD ≌△COB(AAS).∴OD=OB.
∴四边形ABCD 是平行四边形.
(2)∵四边形ABCD 是平行四边形,AC⊥BD,∴□ABCD的面积:
11.(1)∵点E、F 分别是边AD、BC的中点,
∵四边形ABCD 是平行四边形,
∴AD=CB,AB=CD,∠ABF=∠CDE,
∴DE=BF.
在△ABF 和△CDE 中 ∴△ABF≌△CDE(SAS).
(2)∵BC∥AD,∴∠FBH=∠EDG.
∵△ABF≌△CDE,∴∠BFH=∠DEG.
在△BFH 和△DEG中,
∴△BFH≌△DEG(ASA),∴FH=EG.
∵CF∥AE,CF=AE,
∴四边形 AECF 是平行四边形,∴AF∥CE,
∴FH∥EG,又FH=EG,
∴四边形EHFG 是平行四边形.
12.(1)过点 A 作AH⊥BE于点 H,如图(1),
∵OC:EC=5:3,
不妨设OC=5x,则EC=3x,AC=10x,
∴CH=CE+EH=3x+2.
∵四边形 ABCD 是平行四边形,
∴AD∥BC,∴∠ACH=∠DAC=60°,
∴10x=2(3x+2),解得x=1.∴AC=10.
(2)延长EG 至点M,使得 EM=AE,连接AM,如图(2),
∵∠AEG=60°,∴△AEM 为等边三角形,
∴AE=AM,∠M=60°.
∵AB=AE,∴∠ABE=∠AEB,AB=AM.
∵四边形ABCD 是平行四边形,
∴AB∥CD. ∴∠ABC+∠BCD=180°.
∵∠AGB+∠BCD=180°,∴∠ABC=∠AGB.
∵∠AEG=∠ACB=60°,
∴∠AEB+∠CEG=∠CEG+∠CGE=120°,
∴∠AEB=∠CGE.
∵∠AGB=∠ABE=∠AEB,∠AGM=∠CGE,
∴∠AGB=∠AGM.
又AG=AG,∴△ABG≌△AMG(AAS).
∴BG=MG,∴BG+EG=MG+EG=EM.
∵AE=EM,∴AE=BG+EG.
∵四边形ABCD 是平行四边形,∴AB=DC.
∵AB=AE,∴BG+EG=DC.
13.(1)①如图(1),∵四边形 ABCD 是平行四边形,
∴AB∥CD.∴∠DEA=∠EAB.
∵AE 平分∠DAB,∴∠DAE=∠EAB.
∴∠DAE=∠DEA. ∴DE=AD=5.
同理可得BC=CF=5.
∵点E与点F 重合,∴AB=CD=10.
②当点E 与点C重合时,同理可证DE=DC=AD=5.
∵CF=BC=5,∴点 F 与点D 重合.
∴EF=DC=5.
(2)分三种情况讨论:
如图(2),易知AD=DE=EF=CF,∴AD=
如图(3),易知AD=DE,BC=CF.
又
如图(4),∵AD=DE,CB=CF,又
综上所述, 的值为 、 或2.
素养考向 动点问题:所谓“动点问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.
14.(1)根据小明的作法,知CF=AE,
∵四边形ABCD 是平行四边形,∴AD∥BC.
又CF=AE,∴四边形AFCE 是平行四边形,
∴AF∥CE.
(2)以A 为圆心,EC 为半径画弧,交 BC 于点F,此时会有两个交点,只有其中之一符合题意.故小丽的作法有问题.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
