第 1课时 矩形 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 第 1课时 矩形 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第 1课时 矩 形(1)
1. 如图,在矩形ABCD 中,对角线 AC 与 BD 相交于点O,则下列结论一定正确的是( ).
A. AB=AD
B. AC⊥BD
C. AC=BD
D. ∠ACB=∠ACD
2.(2023·十堰中考)如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( ).
A.四边形 ABCD 由矩形变为平行四边形
B.对角线 BD 的长度减小
C.四边形ABCD的面积不变
D.四边形 ABCD 的周长不变
3.如图,矩形OBCD 的顶点C 的坐标为(1,3),则 BD= .
4.(2024·连云港外国语学校一模改编)如图,矩形ABCD的对角线AC、BD 相交于点O,点E、F 在BD上,BE=DF.求证:AE=CF.
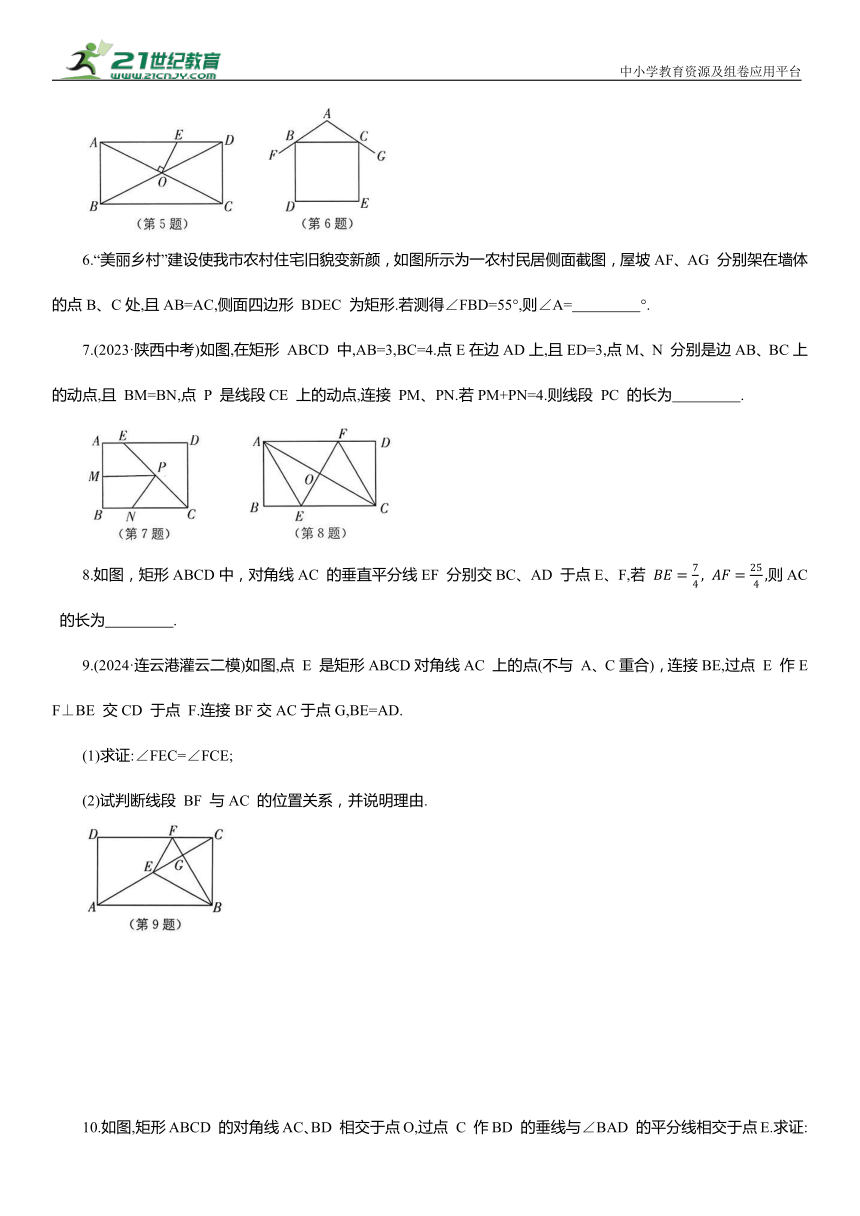
5.如图,在矩形 ABCD 中,AB=4,BC=8,对角线AC、BD 相交于点O,过点 O 作OE⊥AC交AD 于点E,则DE 的长是( ).
A. 3 B. 5 C. 2.4 D. 2.5
6.“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF、AG 分别架在墙体的点B、C处,且AB=AC,侧面四边形 BDEC 为矩形.若测得∠FBD=55°,则∠A= °.
7.(2023·陕西中考)如图,在矩形 ABCD 中,AB=3,BC=4.点E在边AD上,且ED=3,点M、N 分别是边AB、BC上的动点,且 BM=BN,点 P 是线段CE 上的动点,连接 PM、PN.若PM+PN=4.则线段 PC 的长为 .
8.如图,矩形ABCD中,对角线AC 的垂直平分线EF 分别交BC、AD 于点E、F,若 则AC 的长为 .
9.(2024·连云港灌云二模)如图,点 E 是矩形ABCD对角线AC 上的点(不与 A、C重合),连接BE,过点 E 作EF⊥BE 交CD 于点 F.连接BF交AC于点G,BE=AD.
(1)求证:∠FEC=∠FCE;
(2)试判断线段 BF 与AC 的位置关系,并说明理由.
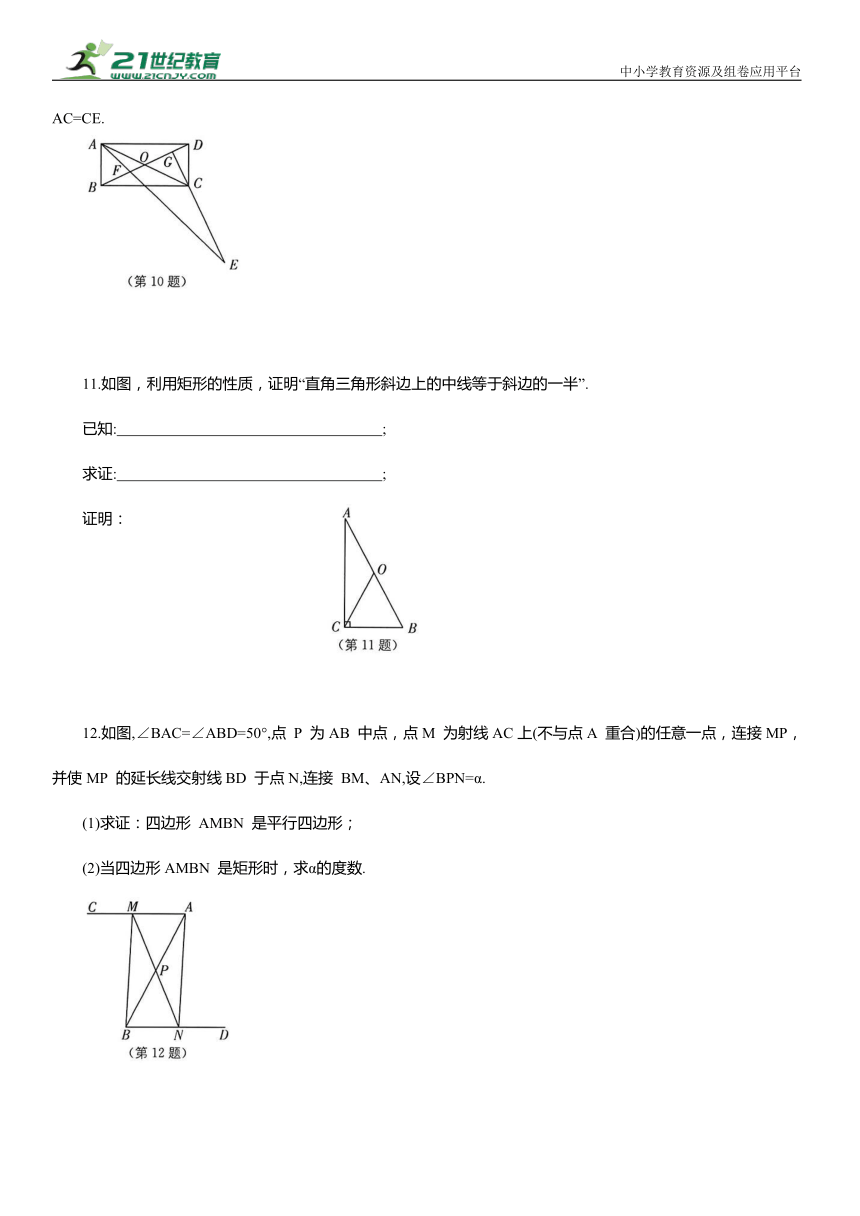
10.如图,矩形ABCD 的对角线AC、BD 相交于点O,过点 C 作BD 的垂线与∠BAD 的平分线相交于点E.求证:AC=CE.
11.如图,利用矩形的性质,证明“直角三角形斜边上的中线等于斜边的一半”.
已知: ;
求证: ;
证明:
12.如图,∠BAC=∠ABD=50°,点 P 为AB 中点,点M 为射线AC上(不与点A 重合)的任意一点,连接MP,并使MP 的延长线交射线BD 于点N,连接 BM、AN,设∠BPN=α.
(1)求证:四边形 AMBN 是平行四边形;
(2)当四边形AMBN 是矩形时,求α的度数.
13.(2024·陕西中考)如图,四边形 ABCD 是矩形,点E 和点F 在边BC 上,且BE=CF,求证:AF=DE.
第1课时 矩 形(1)
1. C [解析]∵四边形ABCD 是矩形,
∴AC=BD,∠ADC =90°,AD =BC,AD∥BC,OA= AC,∴AB =AD、AC⊥BD、∠ACB =∠ACD 不一定成立,AC=BD 一定成立.故选C.
2. C [解析]向左扭动矩形框架ABCD,只改变四边形的形状,四边形变成平行四边形,A不符合题意;向左扭动框架,此时对角线BD 减小,对角线AC增大,B不符合题意;向左扭动框架,BC边上的高减小,故面积变小,C符合题意;向左扭动框架,四边形的四条边不变,故周长不变,D不符合题意.故选C.
[解析]连接OC,
∵四边形OBCD 是矩形,.
4.∵四边形ABCD 是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,∴OE=OF,
在△AOE 和△COF 中,
∴△AOE≌△COF(SAS),∴AE=CF.
5. A [解析]如图,连接CE,
∵在矩形 ABCD 中,AB=4,BC=8,∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC.
∵OE⊥AC,∴AE=CE.设DE=x,
则AE=CE=8-x.
在 Rt△CDE 中,由勾股定理,得 解得x=3.
∴DE 的长为3.故选 A.
6.110 [解析]∵四边形 BDEC 为矩形,∴∠DBC=90°.∵∠FBD =55°,∴∠ABC=180°-∠DBC-∠FBD=35°.∵AB=AC,∴∠ABC=∠ACB=35°,∴∠A=180°-∠ABC-∠ACB=110°.
7. [解析]∵DE=AB=CD=3,∴△CDE 是等腰直角三角形.
作点 N 关于EC 的对称点 N',则点 N'在直线CD上,连接PN',如图,
∵PM+PN=4.∴PM+PN'=4=BC,即 此时M、P、N'三点共线且MN'∥AD,点 P 在MN'的中点处,
8.10 [解析]∵EF 是AC的垂直平分线,∴AO=CO.
∵四边形 ABCD 是矩形,
∴AD∥BC,∴∠OAF=∠OCE.
在△AOF 和△COE 中,
∴△AOF ≌△COE(ASA),∴AF=CE=
∵EF 是AC的垂直平分线,
又
在Rt△ABE 中,
在 Rt△ABC中,
思路引导 本题考查矩形的性质、线段垂直平分线的性质,解题关键是利用垂直平分线的性质以及矩形的性质证明△AOF≌△COE,进而得到AF=CE= ,再利用勾股定理求出AB和AC的长.
9.(1)∵四边形ABCD 是矩形,
∴AD=BC,∠DCB=90°.
∵BE=AD,∴BC=BE,∴∠BEC=∠BCE.
∵EF⊥BE,∴∠BEF=∠DCB=90°,
∴∠FEC=∠FCE.
(2)BF⊥AC.理由如下:
∵∠FEC=∠FCE,∴EF=CF.
∵BE=BC,∴BF垂直平分CE,∴BF⊥AC.
10.如图,过点 A 作AH⊥BD 于点H,
∵GE⊥BD,∴AH∥CE.∴∠HAE=∠E.
在Rt△ABD 和 Rt△AHB 中,∠1+∠ABD=90°,∠ABD+∠2=90°,∴∠1=∠2.
∵四边形ABCD 是矩形,
∴OA=OD.∴∠2=∠3.∴∠1=∠3.
∵AE平分∠BAD,∴∠BAE=∠DAE.
∴∠BAE-∠1=∠DAE-∠3,
即∠HAE=∠CAE.
∴∠E=∠CAE.∴AC=CE.
11.已知:在Rt△ABC中,∠ACB=90°,CO 是斜边AB上的中线.
求证:
证明:如图,延长CO至点E,使CO=OE,连接AE、BE,
∵CO=OE,点O为AB中点,
∴OA=OB,
∴四边形ACBE 为平行四边形.
∵∠ACB=90°,∴平行四边形AEBC是矩形,
12.(1)∵∠BAC=∠ABD=50°,∴AM∥BN.
∵P为AB 中点,∴AP=BP.∵∠APM=∠BPN,易证△APM≌△BPN(ASA),
∴AM=BN,∴四边形AMBN 是平行四边形.
(2)∵四边形AMBN 是矩形,
∴AB=MN,PB=PN,
∴△PBN 是等腰三角形,
∴∠PBN=∠BNP=50°.
∴在△PBN 中,∠BPN=180°-2∠PBN=80°,即α=80°.
13.∵四边形ABCD 为矩形,
∴AB=CD,∠B=∠C=90°.
∵BE=CF,∴BE+EF=CF+EF.即BF=CE.
在△ABF 和△DCE 中,
∴△ABF≌△DCE(SAS),∴AF=DE.
第 1课时 矩 形(1)
1. 如图,在矩形ABCD 中,对角线 AC 与 BD 相交于点O,则下列结论一定正确的是( ).
A. AB=AD
B. AC⊥BD
C. AC=BD
D. ∠ACB=∠ACD
2.(2023·十堰中考)如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( ).
A.四边形 ABCD 由矩形变为平行四边形
B.对角线 BD 的长度减小
C.四边形ABCD的面积不变
D.四边形 ABCD 的周长不变
3.如图,矩形OBCD 的顶点C 的坐标为(1,3),则 BD= .
4.(2024·连云港外国语学校一模改编)如图,矩形ABCD的对角线AC、BD 相交于点O,点E、F 在BD上,BE=DF.求证:AE=CF.
5.如图,在矩形 ABCD 中,AB=4,BC=8,对角线AC、BD 相交于点O,过点 O 作OE⊥AC交AD 于点E,则DE 的长是( ).
A. 3 B. 5 C. 2.4 D. 2.5
6.“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF、AG 分别架在墙体的点B、C处,且AB=AC,侧面四边形 BDEC 为矩形.若测得∠FBD=55°,则∠A= °.
7.(2023·陕西中考)如图,在矩形 ABCD 中,AB=3,BC=4.点E在边AD上,且ED=3,点M、N 分别是边AB、BC上的动点,且 BM=BN,点 P 是线段CE 上的动点,连接 PM、PN.若PM+PN=4.则线段 PC 的长为 .
8.如图,矩形ABCD中,对角线AC 的垂直平分线EF 分别交BC、AD 于点E、F,若 则AC 的长为 .
9.(2024·连云港灌云二模)如图,点 E 是矩形ABCD对角线AC 上的点(不与 A、C重合),连接BE,过点 E 作EF⊥BE 交CD 于点 F.连接BF交AC于点G,BE=AD.
(1)求证:∠FEC=∠FCE;
(2)试判断线段 BF 与AC 的位置关系,并说明理由.
10.如图,矩形ABCD 的对角线AC、BD 相交于点O,过点 C 作BD 的垂线与∠BAD 的平分线相交于点E.求证:AC=CE.
11.如图,利用矩形的性质,证明“直角三角形斜边上的中线等于斜边的一半”.
已知: ;
求证: ;
证明:
12.如图,∠BAC=∠ABD=50°,点 P 为AB 中点,点M 为射线AC上(不与点A 重合)的任意一点,连接MP,并使MP 的延长线交射线BD 于点N,连接 BM、AN,设∠BPN=α.
(1)求证:四边形 AMBN 是平行四边形;
(2)当四边形AMBN 是矩形时,求α的度数.
13.(2024·陕西中考)如图,四边形 ABCD 是矩形,点E 和点F 在边BC 上,且BE=CF,求证:AF=DE.
第1课时 矩 形(1)
1. C [解析]∵四边形ABCD 是矩形,
∴AC=BD,∠ADC =90°,AD =BC,AD∥BC,OA= AC,∴AB =AD、AC⊥BD、∠ACB =∠ACD 不一定成立,AC=BD 一定成立.故选C.
2. C [解析]向左扭动矩形框架ABCD,只改变四边形的形状,四边形变成平行四边形,A不符合题意;向左扭动框架,此时对角线BD 减小,对角线AC增大,B不符合题意;向左扭动框架,BC边上的高减小,故面积变小,C符合题意;向左扭动框架,四边形的四条边不变,故周长不变,D不符合题意.故选C.
[解析]连接OC,
∵四边形OBCD 是矩形,.
4.∵四边形ABCD 是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,∴OE=OF,
在△AOE 和△COF 中,
∴△AOE≌△COF(SAS),∴AE=CF.
5. A [解析]如图,连接CE,
∵在矩形 ABCD 中,AB=4,BC=8,∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC.
∵OE⊥AC,∴AE=CE.设DE=x,
则AE=CE=8-x.
在 Rt△CDE 中,由勾股定理,得 解得x=3.
∴DE 的长为3.故选 A.
6.110 [解析]∵四边形 BDEC 为矩形,∴∠DBC=90°.∵∠FBD =55°,∴∠ABC=180°-∠DBC-∠FBD=35°.∵AB=AC,∴∠ABC=∠ACB=35°,∴∠A=180°-∠ABC-∠ACB=110°.
7. [解析]∵DE=AB=CD=3,∴△CDE 是等腰直角三角形.
作点 N 关于EC 的对称点 N',则点 N'在直线CD上,连接PN',如图,
∵PM+PN=4.∴PM+PN'=4=BC,即 此时M、P、N'三点共线且MN'∥AD,点 P 在MN'的中点处,
8.10 [解析]∵EF 是AC的垂直平分线,∴AO=CO.
∵四边形 ABCD 是矩形,
∴AD∥BC,∴∠OAF=∠OCE.
在△AOF 和△COE 中,
∴△AOF ≌△COE(ASA),∴AF=CE=
∵EF 是AC的垂直平分线,
又
在Rt△ABE 中,
在 Rt△ABC中,
思路引导 本题考查矩形的性质、线段垂直平分线的性质,解题关键是利用垂直平分线的性质以及矩形的性质证明△AOF≌△COE,进而得到AF=CE= ,再利用勾股定理求出AB和AC的长.
9.(1)∵四边形ABCD 是矩形,
∴AD=BC,∠DCB=90°.
∵BE=AD,∴BC=BE,∴∠BEC=∠BCE.
∵EF⊥BE,∴∠BEF=∠DCB=90°,
∴∠FEC=∠FCE.
(2)BF⊥AC.理由如下:
∵∠FEC=∠FCE,∴EF=CF.
∵BE=BC,∴BF垂直平分CE,∴BF⊥AC.
10.如图,过点 A 作AH⊥BD 于点H,
∵GE⊥BD,∴AH∥CE.∴∠HAE=∠E.
在Rt△ABD 和 Rt△AHB 中,∠1+∠ABD=90°,∠ABD+∠2=90°,∴∠1=∠2.
∵四边形ABCD 是矩形,
∴OA=OD.∴∠2=∠3.∴∠1=∠3.
∵AE平分∠BAD,∴∠BAE=∠DAE.
∴∠BAE-∠1=∠DAE-∠3,
即∠HAE=∠CAE.
∴∠E=∠CAE.∴AC=CE.
11.已知:在Rt△ABC中,∠ACB=90°,CO 是斜边AB上的中线.
求证:
证明:如图,延长CO至点E,使CO=OE,连接AE、BE,
∵CO=OE,点O为AB中点,
∴OA=OB,
∴四边形ACBE 为平行四边形.
∵∠ACB=90°,∴平行四边形AEBC是矩形,
12.(1)∵∠BAC=∠ABD=50°,∴AM∥BN.
∵P为AB 中点,∴AP=BP.∵∠APM=∠BPN,易证△APM≌△BPN(ASA),
∴AM=BN,∴四边形AMBN 是平行四边形.
(2)∵四边形AMBN 是矩形,
∴AB=MN,PB=PN,
∴△PBN 是等腰三角形,
∴∠PBN=∠BNP=50°.
∴在△PBN 中,∠BPN=180°-2∠PBN=80°,即α=80°.
13.∵四边形ABCD 为矩形,
∴AB=CD,∠B=∠C=90°.
∵BE=CF,∴BE+EF=CF+EF.即BF=CE.
在△ABF 和△DCE 中,
∴△ABF≌△DCE(SAS),∴AF=DE.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
