第5课时 正方形 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 第5课时 正方形 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 274.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 05:25:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第5课时 正 方 形
1.(2024·无锡新吴区期中)给出下列判断:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线相等的四边形是矩形;
③对角线互相垂直且相等的四边形是正方形;
④有一条对角线平分一个内角的平行四边形为菱形.
其中,不正确的有( ).
A. 1个 B. 2个 C. 3个 D. 4个
2.(2024·盐城阜宁期中)如图,在正方形ABCD 中,F为边AB 上一点,CF 与BD 交于点E,连接AE,若∠BCF=25°,则∠AEF=( ).
A. 35° B. 40° C. 45° D. 50°
3.(2024·南京鼓楼区期末)如图,在平面直角坐标系中,正方形 ABCD 的两个顶点 A、B 坐标分别为(--2,0)、(0, ),则C点的坐标为 .
4.如图,四边形ABCD 是正方形,E、F 是AD、DC上的点,且∠EBF=45°,则 EF 与CF+AE 相等吗 说明理由.
5.如图,点 E、F、G、H 分别在矩形ABCD(AB>AD)的四条边上,连接EF、FG、GH、HE,得到四边形 EFGH.下列关于四边形 EFGH的说法正确的是( ).
①存在无数个四边形 EFGH 是平行四边形;
②存在无数个四边形 EFGH 是菱形;
③存在无数个四边形 EFGH 是矩形;
④存在无数个四边形 EFGH 是正方形.
A. ① B. ①②
C. ①②③ D. ①②③④
6.(2024·常州天宁区期中)如图,正方形 ABCD 的边长为2,点E 是CD的中点,HG 垂直平分AE 且分别交AE、BC 于点H、G,则BG= .
7.如图(1),小明用四根相同长度的木条制作了一个正方形学具,测得AB=2cm,将正方形学具变形为菱形(如图(2)),且∠ABC=60°,则图(2)中三角形 ABD 的面积为 .
8.如图,在 Rt△ABC 与 Rt△ABD 中,∠ABC=∠BAD=90°,AD=BC,AC、BD 相交于点 G,过点A 作AE∥DB 交CB 的延长线于点E,过点 B 作 BF∥CA 交 DA 的延长线于点 F,AE、BF 相交于点H.
(1)说明四边形AHBG 是菱形的理由.
(2)若使四边形AHBG 是正方形,还需在 Rt△ABC的边长之间再添加一个什么条件 请你写出这个条件.(不必证明)
9.如图,已知菱形ABCD 的对角线AC与BD 相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD 是正方形;
(2)E 是OB 上一点,DH⊥CE,垂足为 H,DH 与OC 相交于点F,求证:OE=OF.
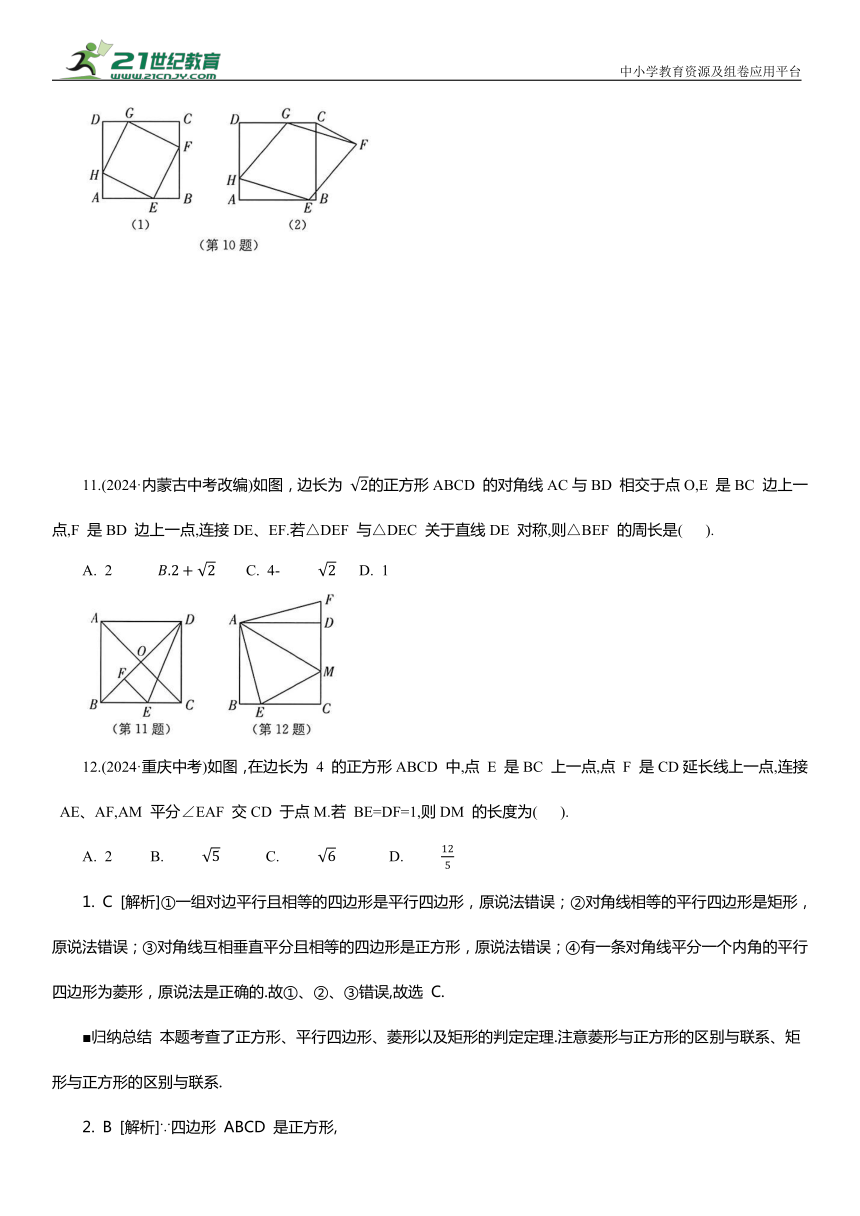
10. 如图,正方形 ABCD 的边长为6,菱形 EFGH 的三个顶点E、G、H 分别在正方形 ABCD 的边AB、CD、DA 上,AH=2.
(1)如图(1),当DG=2时,求证:菱形EFGH 是正方形;
(2)如图(2),连接CF,当△FCG 的面积等于1时,求线段DG 的长度.
11.(2024·内蒙古中考改编)如图,边长为 的正方形ABCD 的对角线AC与BD 相交于点O,E 是BC 边上一点,F 是BD 边上一点,连接DE、EF.若△DEF 与△DEC 关于直线DE 对称,则△BEF 的周长是( ).
A. 2 C. 4- D. 1
12.(2024·重庆中考)如图,在边长为 4 的正方形ABCD 中,点 E 是BC 上一点,点 F 是CD延长线上一点,连接 AE、AF,AM 平分∠EAF 交CD 于点M.若 BE=DF=1,则DM 的长度为( ).
A. 2 B. C. D.
1. C [解析]①一组对边平行且相等的四边形是平行四边形,原说法错误;②对角线相等的平行四边形是矩形,原说法错误;③对角线互相垂直平分且相等的四边形是正方形,原说法错误;④有一条对角线平分一个内角的平行四边形为菱形,原说法是正确的.故①、②、③错误,故选 C.
■归纳总结 本题考查了正方形、平行四边形、菱形以及矩形的判定定理.注意菱形与正方形的区别与联系、矩形与正方形的区别与联系.
2. B [解析]∵四边形 ABCD 是正方形,
∴AB=BC,∠ABE=∠CBE=45°,
易证△ABE≌△CBE(SAS),∴∠BEC=∠AEB.
∵∠BCF=25°,∴∠BEC=180°-25°-45°=110°=∠AEB,∴∠DEC=∠BEF=70°,
故选B.
[解析]如图,过点C作CE⊥y轴于点E,∴∠BEC=90°.
由正方形 ABCD 的两个顶点A、B坐标分别为(-2,0)、(0, ),得AO=2,BO=
∵四边形 ABCD 是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°.
∵∠AOB=90°,∴∠ABO+∠OAB=90°,
∴∠CBE=∠OAB.
在△AOB 和△BEC中,
∴△AOB≌△BEC(AAS),∴AO=BE=2,BO=
4. EF=CF+AE.理由如下:
延长FC到点P,使CP=AE,连接BP.
∵四边形ABCD 是正方形,
∴AB=BC,∠A=∠BCD=∠BCP=90°.
∵AE=CP,∴△ABE≌△CBP(SAS).
∴BE=BP,∠ABE=∠CBP.
∵∠ABC=∠ABE+∠EBC=90°,
∴∠CBP+∠EBC=90°,即∠EBP=90°.
∵∠EBF=45°,∠PBF=∠EBP-∠EBF=90°-45°=45°,∴∠EBF=∠PBF=45°.
∵BE=BP,BF=BF,
∴△EBF≌△PBF(SAS).∴EF=PF.
∵PF=PC+CF,CP=AE,∴EF=CF+AE.
5. C [解析]①如图,∵四边形 ABCD 是矩形,连接AC、BD交于点O,
过点O 作直线EG 和HF,分别交 AB、BC、CD、AD于E、F、G、H,则四边形EFGH 是平行四边形,故存在无数个四边形EFGH 是平行四边形.故①正确;②当EG⊥HF 时,存在无数个四边形 EFGH 是菱形.故②正确;
③当EG=HF时,四边形EFGH 是矩形,故存在无数个四边形 EFGH 是矩形.故③正确;
④当四边形 EFGH 是正方形时,EH=EF,则易证△AEH≌△BFE(AAS),∴AH=BE,AE=BF.
∵BF=DH,∴AB=AD,∴四边形 ABCD 是正方形.当四边形 ABCD 为正方形时,四边形 EFGH 是正方形.故④错误.故选 C.
6. [解析]如图,连接AG、EG,
∵HG垂直平分AE,∴AG=EG.
∵正方形ABCD 的边长为2,
∴∠B=∠C=90°,AB=BC=CD=2.
∵E是CD的中点,∴CE=1,设CG=x,则BG=2-x,
由勾股定理,得 解得
[解析]如题图(1),四边形A BCD是 正方形,AB=AD=2cm.
如图,连接AC交BD于O,
∵∠ABC=60°,AB=BC=2cm.
∴△ABC 是等边三角形,则AC=2cm.
∵四边形 ABCD 是菱形,
∴AO= AC=1cm,BO=DO,AC⊥BD,
8.(1)∵AH∥GB,BH∥GA,
∴四边形AHBG 为平行四边形.
在△ABC 和△BAD中
∴△ABC≌△BAD(SAS),∴∠ABD=∠BAC.
∴GA=GB.∴平行四边形AHBG是菱形.
(2)AB=BC.
9.(1)∵四边形ABCD 是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°.
∵∠CAD=∠DBC,∴∠BAD=∠ABC,
∴2∠BAD=180°,∴∠BAD=90°,
∴菱形ABCD 是正方形.
(2)∵四边形 ABCD 是正方形,
∴∠COB=∠DOC=90°,CO=DO.
∵DH⊥CE,垂足为 H,
∴∠DHE=90°,∴∠EDH+∠DEH=90°.
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH.
在△ECO和△FDO中
∴△ECO≌△FDO(ASA),∴OE=OF.
10.(1)∵四边形ABCD是正方形,∴∠D=∠A=90°.
∵四边形EFGH 是菱形,∴HG=HE.
在Rt△DHG 和△AEH 中,
∴Rt△DHG≌△AEH(HL),
∴∠DHG=∠AEH,∴∠DHG+∠AHE=90°,
∴∠GHE=90°,∴菱形 EFGH 为正方形.
(2)如图,过点 F 作FM⊥CD,交DC的延长线于点M,连接GE.
∵CD∥AB,∴∠AEG=∠MGE.∵GF∥HE,
∴∠HEG=∠FGE,∴∠AEH=∠FGM.
在△EHA 和△GFM中
∴△EHA≌△GFM(AAS),∴MF=AH=2.设DG=x,则( 6-x=1.解得x=5,即DG=5.
11. A [解析]∵正方形 ABCD 的边长是
∵△DEF 与△DEC 关于直线DE 对称,
的周长=BF+BE+EF=BF+BE+EC=BF+BC=2- + =2.故选 A.
12. D [解析]∵四边形ABCD 是正方形,
∴AB=AD,∠ABE=∠ADM=∠ADF=90°.
在 Rt△ABE 和 Rt△ADF 中,
∴Rt△ABE≌Rt△ADF(SAS),∴AE=AF.
∵AM平分∠EAF,∴∠EAM=∠FAM.
在△AEM 和△AFM中,
∴△AEM≌△AFM(SAS),∴EM=FM.
∵四边形ABCD 是正方形,
∴BC=CD=4,∠BCD=90°,
设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4--1=3,EM=FM=FD+DM=1+x,在 Rt△MCE 中,根据勾股定理,得 CE ,即( 解得 故选 D.
第5课时 正 方 形
1.(2024·无锡新吴区期中)给出下列判断:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线相等的四边形是矩形;
③对角线互相垂直且相等的四边形是正方形;
④有一条对角线平分一个内角的平行四边形为菱形.
其中,不正确的有( ).
A. 1个 B. 2个 C. 3个 D. 4个
2.(2024·盐城阜宁期中)如图,在正方形ABCD 中,F为边AB 上一点,CF 与BD 交于点E,连接AE,若∠BCF=25°,则∠AEF=( ).
A. 35° B. 40° C. 45° D. 50°
3.(2024·南京鼓楼区期末)如图,在平面直角坐标系中,正方形 ABCD 的两个顶点 A、B 坐标分别为(--2,0)、(0, ),则C点的坐标为 .
4.如图,四边形ABCD 是正方形,E、F 是AD、DC上的点,且∠EBF=45°,则 EF 与CF+AE 相等吗 说明理由.
5.如图,点 E、F、G、H 分别在矩形ABCD(AB>AD)的四条边上,连接EF、FG、GH、HE,得到四边形 EFGH.下列关于四边形 EFGH的说法正确的是( ).
①存在无数个四边形 EFGH 是平行四边形;
②存在无数个四边形 EFGH 是菱形;
③存在无数个四边形 EFGH 是矩形;
④存在无数个四边形 EFGH 是正方形.
A. ① B. ①②
C. ①②③ D. ①②③④
6.(2024·常州天宁区期中)如图,正方形 ABCD 的边长为2,点E 是CD的中点,HG 垂直平分AE 且分别交AE、BC 于点H、G,则BG= .
7.如图(1),小明用四根相同长度的木条制作了一个正方形学具,测得AB=2cm,将正方形学具变形为菱形(如图(2)),且∠ABC=60°,则图(2)中三角形 ABD 的面积为 .
8.如图,在 Rt△ABC 与 Rt△ABD 中,∠ABC=∠BAD=90°,AD=BC,AC、BD 相交于点 G,过点A 作AE∥DB 交CB 的延长线于点E,过点 B 作 BF∥CA 交 DA 的延长线于点 F,AE、BF 相交于点H.
(1)说明四边形AHBG 是菱形的理由.
(2)若使四边形AHBG 是正方形,还需在 Rt△ABC的边长之间再添加一个什么条件 请你写出这个条件.(不必证明)
9.如图,已知菱形ABCD 的对角线AC与BD 相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD 是正方形;
(2)E 是OB 上一点,DH⊥CE,垂足为 H,DH 与OC 相交于点F,求证:OE=OF.
10. 如图,正方形 ABCD 的边长为6,菱形 EFGH 的三个顶点E、G、H 分别在正方形 ABCD 的边AB、CD、DA 上,AH=2.
(1)如图(1),当DG=2时,求证:菱形EFGH 是正方形;
(2)如图(2),连接CF,当△FCG 的面积等于1时,求线段DG 的长度.
11.(2024·内蒙古中考改编)如图,边长为 的正方形ABCD 的对角线AC与BD 相交于点O,E 是BC 边上一点,F 是BD 边上一点,连接DE、EF.若△DEF 与△DEC 关于直线DE 对称,则△BEF 的周长是( ).
A. 2 C. 4- D. 1
12.(2024·重庆中考)如图,在边长为 4 的正方形ABCD 中,点 E 是BC 上一点,点 F 是CD延长线上一点,连接 AE、AF,AM 平分∠EAF 交CD 于点M.若 BE=DF=1,则DM 的长度为( ).
A. 2 B. C. D.
1. C [解析]①一组对边平行且相等的四边形是平行四边形,原说法错误;②对角线相等的平行四边形是矩形,原说法错误;③对角线互相垂直平分且相等的四边形是正方形,原说法错误;④有一条对角线平分一个内角的平行四边形为菱形,原说法是正确的.故①、②、③错误,故选 C.
■归纳总结 本题考查了正方形、平行四边形、菱形以及矩形的判定定理.注意菱形与正方形的区别与联系、矩形与正方形的区别与联系.
2. B [解析]∵四边形 ABCD 是正方形,
∴AB=BC,∠ABE=∠CBE=45°,
易证△ABE≌△CBE(SAS),∴∠BEC=∠AEB.
∵∠BCF=25°,∴∠BEC=180°-25°-45°=110°=∠AEB,∴∠DEC=∠BEF=70°,
故选B.
[解析]如图,过点C作CE⊥y轴于点E,∴∠BEC=90°.
由正方形 ABCD 的两个顶点A、B坐标分别为(-2,0)、(0, ),得AO=2,BO=
∵四边形 ABCD 是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°.
∵∠AOB=90°,∴∠ABO+∠OAB=90°,
∴∠CBE=∠OAB.
在△AOB 和△BEC中,
∴△AOB≌△BEC(AAS),∴AO=BE=2,BO=
4. EF=CF+AE.理由如下:
延长FC到点P,使CP=AE,连接BP.
∵四边形ABCD 是正方形,
∴AB=BC,∠A=∠BCD=∠BCP=90°.
∵AE=CP,∴△ABE≌△CBP(SAS).
∴BE=BP,∠ABE=∠CBP.
∵∠ABC=∠ABE+∠EBC=90°,
∴∠CBP+∠EBC=90°,即∠EBP=90°.
∵∠EBF=45°,∠PBF=∠EBP-∠EBF=90°-45°=45°,∴∠EBF=∠PBF=45°.
∵BE=BP,BF=BF,
∴△EBF≌△PBF(SAS).∴EF=PF.
∵PF=PC+CF,CP=AE,∴EF=CF+AE.
5. C [解析]①如图,∵四边形 ABCD 是矩形,连接AC、BD交于点O,
过点O 作直线EG 和HF,分别交 AB、BC、CD、AD于E、F、G、H,则四边形EFGH 是平行四边形,故存在无数个四边形EFGH 是平行四边形.故①正确;②当EG⊥HF 时,存在无数个四边形 EFGH 是菱形.故②正确;
③当EG=HF时,四边形EFGH 是矩形,故存在无数个四边形 EFGH 是矩形.故③正确;
④当四边形 EFGH 是正方形时,EH=EF,则易证△AEH≌△BFE(AAS),∴AH=BE,AE=BF.
∵BF=DH,∴AB=AD,∴四边形 ABCD 是正方形.当四边形 ABCD 为正方形时,四边形 EFGH 是正方形.故④错误.故选 C.
6. [解析]如图,连接AG、EG,
∵HG垂直平分AE,∴AG=EG.
∵正方形ABCD 的边长为2,
∴∠B=∠C=90°,AB=BC=CD=2.
∵E是CD的中点,∴CE=1,设CG=x,则BG=2-x,
由勾股定理,得 解得
[解析]如题图(1),四边形A BCD是 正方形,AB=AD=2cm.
如图,连接AC交BD于O,
∵∠ABC=60°,AB=BC=2cm.
∴△ABC 是等边三角形,则AC=2cm.
∵四边形 ABCD 是菱形,
∴AO= AC=1cm,BO=DO,AC⊥BD,
8.(1)∵AH∥GB,BH∥GA,
∴四边形AHBG 为平行四边形.
在△ABC 和△BAD中
∴△ABC≌△BAD(SAS),∴∠ABD=∠BAC.
∴GA=GB.∴平行四边形AHBG是菱形.
(2)AB=BC.
9.(1)∵四边形ABCD 是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°.
∵∠CAD=∠DBC,∴∠BAD=∠ABC,
∴2∠BAD=180°,∴∠BAD=90°,
∴菱形ABCD 是正方形.
(2)∵四边形 ABCD 是正方形,
∴∠COB=∠DOC=90°,CO=DO.
∵DH⊥CE,垂足为 H,
∴∠DHE=90°,∴∠EDH+∠DEH=90°.
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH.
在△ECO和△FDO中
∴△ECO≌△FDO(ASA),∴OE=OF.
10.(1)∵四边形ABCD是正方形,∴∠D=∠A=90°.
∵四边形EFGH 是菱形,∴HG=HE.
在Rt△DHG 和△AEH 中,
∴Rt△DHG≌△AEH(HL),
∴∠DHG=∠AEH,∴∠DHG+∠AHE=90°,
∴∠GHE=90°,∴菱形 EFGH 为正方形.
(2)如图,过点 F 作FM⊥CD,交DC的延长线于点M,连接GE.
∵CD∥AB,∴∠AEG=∠MGE.∵GF∥HE,
∴∠HEG=∠FGE,∴∠AEH=∠FGM.
在△EHA 和△GFM中
∴△EHA≌△GFM(AAS),∴MF=AH=2.设DG=x,则( 6-x=1.解得x=5,即DG=5.
11. A [解析]∵正方形 ABCD 的边长是
∵△DEF 与△DEC 关于直线DE 对称,
的周长=BF+BE+EF=BF+BE+EC=BF+BC=2- + =2.故选 A.
12. D [解析]∵四边形ABCD 是正方形,
∴AB=AD,∠ABE=∠ADM=∠ADF=90°.
在 Rt△ABE 和 Rt△ADF 中,
∴Rt△ABE≌Rt△ADF(SAS),∴AE=AF.
∵AM平分∠EAF,∴∠EAM=∠FAM.
在△AEM 和△AFM中,
∴△AEM≌△AFM(SAS),∴EM=FM.
∵四边形ABCD 是正方形,
∴BC=CD=4,∠BCD=90°,
设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4--1=3,EM=FM=FD+DM=1+x,在 Rt△MCE 中,根据勾股定理,得 CE ,即( 解得 故选 D.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
