9.5 三角形的中位线 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 9.5 三角形的中位线 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 05:28:16 | ||
图片预览

文档简介
9.5 三角形的中位线
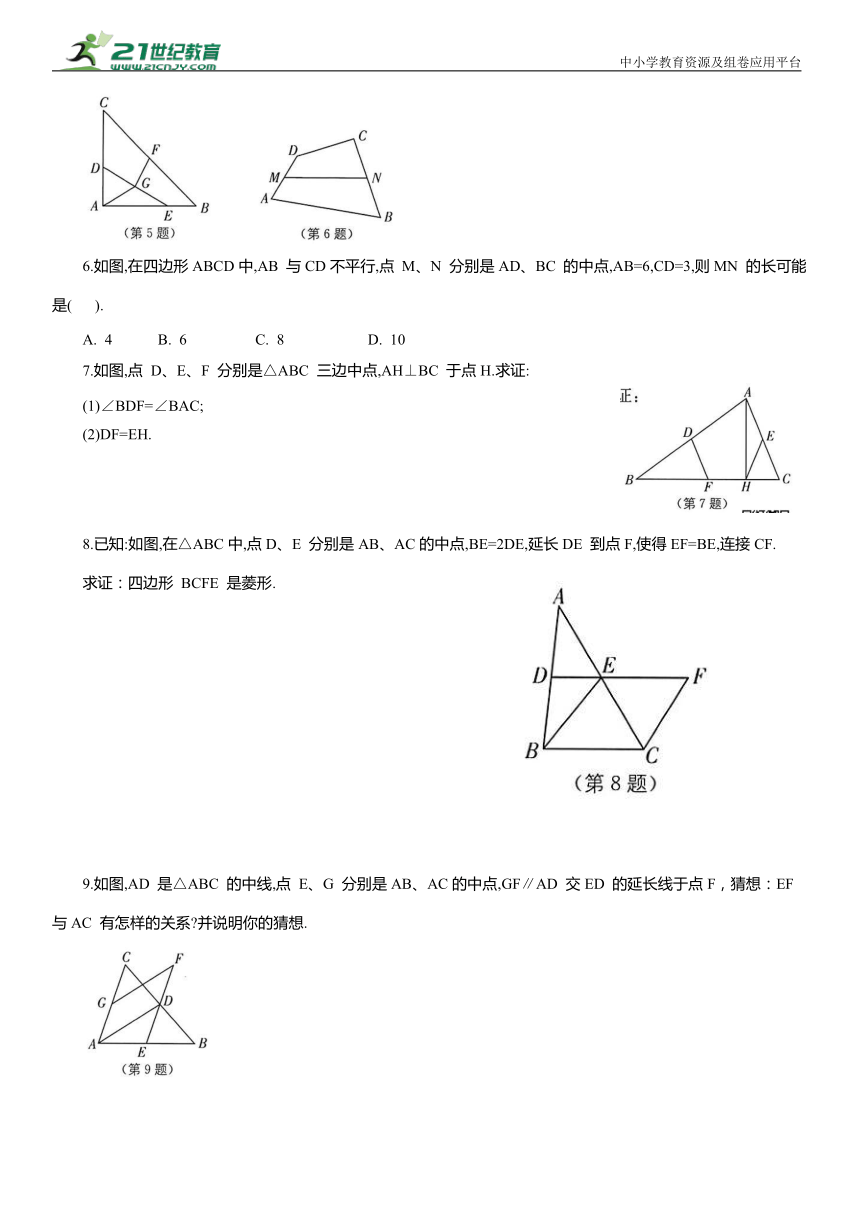
1.(2024·兰州中考)如图,小张想估测被池塘隔开的A、B两处景观之间的距离,他先在 AB 外取一点C,然后步测出 AC、BC 的中点D、E,并步测出 DE 的长约为 18m,由此估测A、B 之间的距离约为( ).
A. 18m B. 24m
C. 36m D. 54m
2.如图,在四边形ABCD 中,点 P 是对角线BD的中点,点 E、F 分别是AB、CD 的中点,AD= BC, ∠CBD = 30°, ∠ADB = 100°, 则∠PFE 的度数是( ).
A. 15° B. 20°
C. 25° D. 35°
3.(2024·盐城东台期中)在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 N 是BC 边上一点.点 M为AB 边上的动点(不与点 B 重合),点D、E分别为CN、MN 的中点,则 DE 的取值范围为( ).
A. 3C. 3≤DE≤4
4.(2024·浙江中考)如图,D、E 分别是△ABC 边AB、AC 的中点,连接 BE、DE.若∠AED=∠BEC,DE=2,则BE 的长为 .
5.如图,在△ABC 中,∠BAC=90°,AB=AC=5,点D 在AC上,且AD=2,点E 是AB上的动点,连接DE,点 F、G 分别是BC 和DE 的中点,连接AG、FG.当AG=FG 时,线段DE长为( ).
D. 4
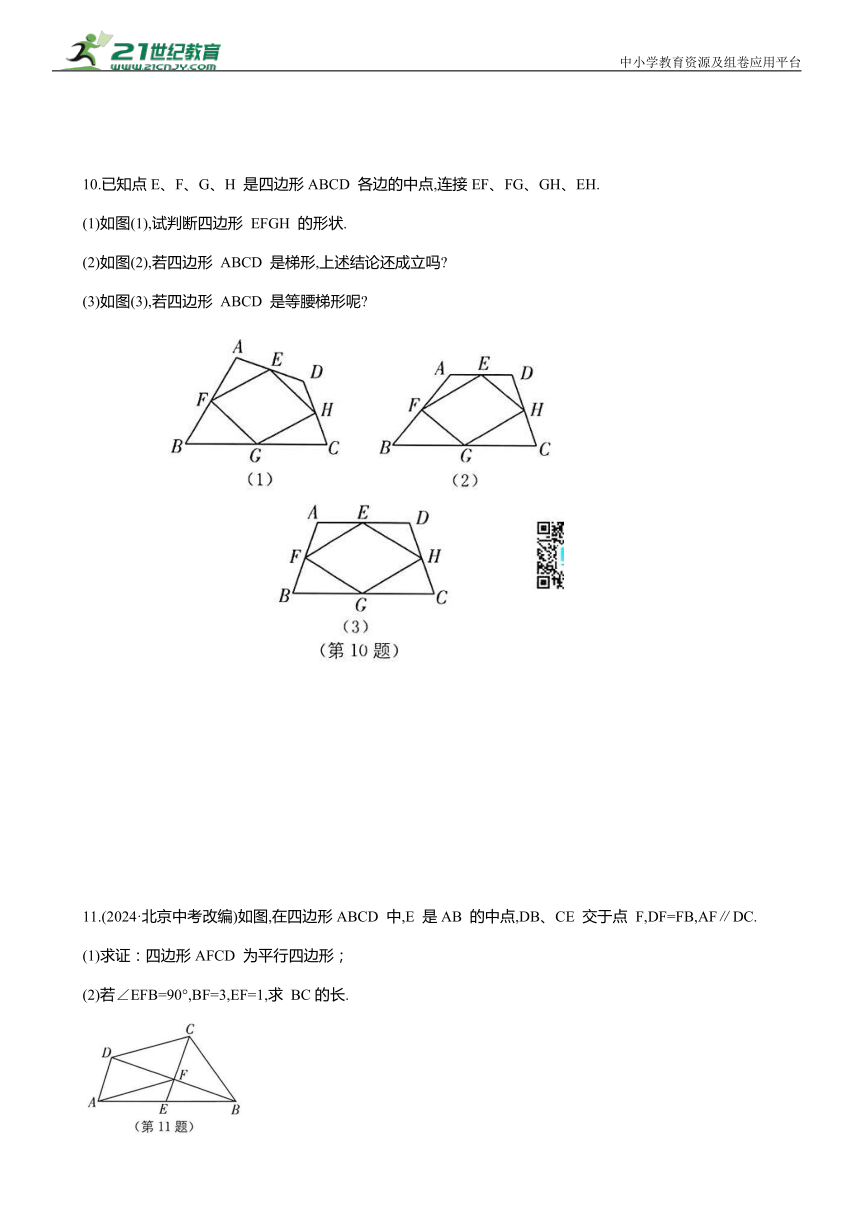
6.如图,在四边形ABCD中,AB 与CD不平行,点 M、N 分别是AD、BC 的中点,AB=6,CD=3,则MN 的长可能是( ).
A. 4 B. 6 C. 8 D. 10
7.如图,点 D、E、F 分别是△ABC 三边中点,AH⊥BC 于点H.求证:
(1)∠BDF=∠BAC;
(2)DF=EH.
8.已知:如图,在△ABC中,点D、E 分别是AB、AC的中点,BE=2DE,延长DE 到点F,使得EF=BE,连接CF.
求证:四边形 BCFE 是菱形.
9.如图,AD 是△ABC 的中线,点 E、G 分别是AB、AC的中点,GF∥AD 交ED 的延长线于点F,猜想:EF 与AC 有怎样的关系 并说明你的猜想.
10.已知点E、F、G、H 是四边形ABCD 各边的中点,连接EF、FG、GH、EH.
(1)如图(1),试判断四边形 EFGH 的形状.
(2)如图(2),若四边形 ABCD 是梯形,上述结论还成立吗
(3)如图(3),若四边形 ABCD 是等腰梯形呢
11.(2024·北京中考改编)如图,在四边形ABCD 中,E 是AB 的中点,DB、CE 交于点 F,DF=FB,AF∥DC.
(1)求证:四边形AFCD 为平行四边形;
(2)若∠EFB=90°,BF=3,EF=1,求 BC的长.
中小学教育资源及组卷应用平台
9.5 三角形的中位线
1. C [解析]∵D、E 分别是AC、BC的中点,
∴DE 是△ABC的中位线.
∴根据三角形的中位线定理,得AB=2DE=36m.故选 C.
2. D [解析]∵点 P 是 BD 的中点,点 F 是DC 的中点,∴PF 是△DBC的中位线,
∴PF= BC,PF∥BC,∴∠FPD=∠CBD=30°.
同理
∴∠EPD=180°-∠ADB=80°.∴∠EPF=110°.
∵AD=BC,∴EP=FP,
故选 D.
3. D [解析]连接CM,
∵∠C=90°,AC=6,BC=8,
∵点 D、E 分别为CN、MN的中点,
∴当CM最小时,DE 取最小值,当CM⊥AB时,CM 取最小值.
即 6×8=10CM,
解得
即 DE 的最小值为
∵CM≤BC,∴CM<8,∴DE<4,
故选 D.
■归纳总结 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
4.4 [解析]∵D、E 分别是△ABC 的边 AB、AC 的中点,
∴BC=2DE=2×2=4,DE∥BC,∴∠AED=∠C.
∵∠AED=∠BEC,∴∠BEC=∠C,
∴BE=BC=4.
5. A [解析]如图,分别过点G、F作AB 的垂线,垂足为M、N,过点G作GP⊥FN 于点 P,
∴四边形GMNP 是矩形,∴GM=PN,GP=MN.
∵∠BAC=90°,AB=AC=5,∴CA⊥AB,∴MG∥AC,NF∥AC.
又点G 和点F 分别是DE 和BC 的中点,GM、FN分别为△ADE 和△ABC的中位线,
设AE=m,则
在 Rt△AGM中,
在Rt△GPF中,
解得m=3,即AE=3,
在Rt△ADE 中,
6. A [解析]如图,连接BD,取 BD 的中点E,连接ME、NE.
∵点M是AD的中点,点E是BD的中点,
同理
在△MNE中,3--1.57.(1)∵点 D、F 分别是边AB、BC的中点,
∴DF 是△ABC的中位线,
∴∠BDF=∠BAC.
(2)∵AH⊥BC于点H,点 E 是AC的中点,
8.∵BE=2DE,EF=BE,∴EF=2DE.
∵D、E分别是AB、AC的中点,
∴BC=2DE且DE∥BC,∴EF=BC.又EF∥BC,
∴四边形 BCFE 是平行四边形.
又 EF=BE,∴四边形 BCFE 是菱形.
9. EF∥AC且EF=AC.理由如下:
∵ED 是△ABC的中位线,
又GF∥AD,∴四边形AGFD 是平行四边形.
∴AC∥EF,AC=EF.
10.(1)四边形 EFGH 是平行四边形.理由如下:连接BD.
∵点 E、F、G、H 是四边形ABCD 各边的中点,
∴EF 是△ABD 的中位线,GH 是△BCD 的中位线.
∴EF=GH,EF∥GH.
∴四边形 EFGH 是平行四边形.
(2)结论成立.
(3)四边形 EFGH 是菱形.理由如下:
连接AC、BD.
∵四边形ABCD 为等腰梯形,∴AC=BD.
同(1)可证四边形 EFGH 是平行四边形.
又 EF 是△ABD的中位线,
又EH 是△ADC的中位线,
∴EF=EH.∴四边形EFGH 是菱形.
11.(1)∵E 是AB 的中点,∴AE=BE.
∵DF=BF,∴EF 是△ABD的中位线,
∴EF∥AD,∴CF∥AD.
又AF∥CD,∴四边形AFCD为平行四边形.
(2)由(1)知,EF 是△ABD的中位线,
∴AD=2EF=2.
∵BF=3,DF=FB,∴DF=BF=3.
∵AD∥CE,∴∠ADF=∠EFB=90°,
∵四边形AFCD为平行四边形,
∵DF=BF,CE⊥BD,∴BC=CD=
解后反思 本题考查了平行四边形的判定和性质、三角形中位线定理、勾股定理,熟练掌握平行四边形的判定和性质定理是解题的关键.
1.(2024·兰州中考)如图,小张想估测被池塘隔开的A、B两处景观之间的距离,他先在 AB 外取一点C,然后步测出 AC、BC 的中点D、E,并步测出 DE 的长约为 18m,由此估测A、B 之间的距离约为( ).
A. 18m B. 24m
C. 36m D. 54m
2.如图,在四边形ABCD 中,点 P 是对角线BD的中点,点 E、F 分别是AB、CD 的中点,AD= BC, ∠CBD = 30°, ∠ADB = 100°, 则∠PFE 的度数是( ).
A. 15° B. 20°
C. 25° D. 35°
3.(2024·盐城东台期中)在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 N 是BC 边上一点.点 M为AB 边上的动点(不与点 B 重合),点D、E分别为CN、MN 的中点,则 DE 的取值范围为( ).
A. 3
4.(2024·浙江中考)如图,D、E 分别是△ABC 边AB、AC 的中点,连接 BE、DE.若∠AED=∠BEC,DE=2,则BE 的长为 .
5.如图,在△ABC 中,∠BAC=90°,AB=AC=5,点D 在AC上,且AD=2,点E 是AB上的动点,连接DE,点 F、G 分别是BC 和DE 的中点,连接AG、FG.当AG=FG 时,线段DE长为( ).
D. 4
6.如图,在四边形ABCD中,AB 与CD不平行,点 M、N 分别是AD、BC 的中点,AB=6,CD=3,则MN 的长可能是( ).
A. 4 B. 6 C. 8 D. 10
7.如图,点 D、E、F 分别是△ABC 三边中点,AH⊥BC 于点H.求证:
(1)∠BDF=∠BAC;
(2)DF=EH.
8.已知:如图,在△ABC中,点D、E 分别是AB、AC的中点,BE=2DE,延长DE 到点F,使得EF=BE,连接CF.
求证:四边形 BCFE 是菱形.
9.如图,AD 是△ABC 的中线,点 E、G 分别是AB、AC的中点,GF∥AD 交ED 的延长线于点F,猜想:EF 与AC 有怎样的关系 并说明你的猜想.
10.已知点E、F、G、H 是四边形ABCD 各边的中点,连接EF、FG、GH、EH.
(1)如图(1),试判断四边形 EFGH 的形状.
(2)如图(2),若四边形 ABCD 是梯形,上述结论还成立吗
(3)如图(3),若四边形 ABCD 是等腰梯形呢
11.(2024·北京中考改编)如图,在四边形ABCD 中,E 是AB 的中点,DB、CE 交于点 F,DF=FB,AF∥DC.
(1)求证:四边形AFCD 为平行四边形;
(2)若∠EFB=90°,BF=3,EF=1,求 BC的长.
中小学教育资源及组卷应用平台
9.5 三角形的中位线
1. C [解析]∵D、E 分别是AC、BC的中点,
∴DE 是△ABC的中位线.
∴根据三角形的中位线定理,得AB=2DE=36m.故选 C.
2. D [解析]∵点 P 是 BD 的中点,点 F 是DC 的中点,∴PF 是△DBC的中位线,
∴PF= BC,PF∥BC,∴∠FPD=∠CBD=30°.
同理
∴∠EPD=180°-∠ADB=80°.∴∠EPF=110°.
∵AD=BC,∴EP=FP,
故选 D.
3. D [解析]连接CM,
∵∠C=90°,AC=6,BC=8,
∵点 D、E 分别为CN、MN的中点,
∴当CM最小时,DE 取最小值,当CM⊥AB时,CM 取最小值.
即 6×8=10CM,
解得
即 DE 的最小值为
∵CM≤BC,∴CM<8,∴DE<4,
故选 D.
■归纳总结 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
4.4 [解析]∵D、E 分别是△ABC 的边 AB、AC 的中点,
∴BC=2DE=2×2=4,DE∥BC,∴∠AED=∠C.
∵∠AED=∠BEC,∴∠BEC=∠C,
∴BE=BC=4.
5. A [解析]如图,分别过点G、F作AB 的垂线,垂足为M、N,过点G作GP⊥FN 于点 P,
∴四边形GMNP 是矩形,∴GM=PN,GP=MN.
∵∠BAC=90°,AB=AC=5,∴CA⊥AB,∴MG∥AC,NF∥AC.
又点G 和点F 分别是DE 和BC 的中点,GM、FN分别为△ADE 和△ABC的中位线,
设AE=m,则
在 Rt△AGM中,
在Rt△GPF中,
解得m=3,即AE=3,
在Rt△ADE 中,
6. A [解析]如图,连接BD,取 BD 的中点E,连接ME、NE.
∵点M是AD的中点,点E是BD的中点,
同理
在△MNE中,3--1.5
∴DF 是△ABC的中位线,
∴∠BDF=∠BAC.
(2)∵AH⊥BC于点H,点 E 是AC的中点,
8.∵BE=2DE,EF=BE,∴EF=2DE.
∵D、E分别是AB、AC的中点,
∴BC=2DE且DE∥BC,∴EF=BC.又EF∥BC,
∴四边形 BCFE 是平行四边形.
又 EF=BE,∴四边形 BCFE 是菱形.
9. EF∥AC且EF=AC.理由如下:
∵ED 是△ABC的中位线,
又GF∥AD,∴四边形AGFD 是平行四边形.
∴AC∥EF,AC=EF.
10.(1)四边形 EFGH 是平行四边形.理由如下:连接BD.
∵点 E、F、G、H 是四边形ABCD 各边的中点,
∴EF 是△ABD 的中位线,GH 是△BCD 的中位线.
∴EF=GH,EF∥GH.
∴四边形 EFGH 是平行四边形.
(2)结论成立.
(3)四边形 EFGH 是菱形.理由如下:
连接AC、BD.
∵四边形ABCD 为等腰梯形,∴AC=BD.
同(1)可证四边形 EFGH 是平行四边形.
又 EF 是△ABD的中位线,
又EH 是△ADC的中位线,
∴EF=EH.∴四边形EFGH 是菱形.
11.(1)∵E 是AB 的中点,∴AE=BE.
∵DF=BF,∴EF 是△ABD的中位线,
∴EF∥AD,∴CF∥AD.
又AF∥CD,∴四边形AFCD为平行四边形.
(2)由(1)知,EF 是△ABD的中位线,
∴AD=2EF=2.
∵BF=3,DF=FB,∴DF=BF=3.
∵AD∥CE,∴∠ADF=∠EFB=90°,
∵四边形AFCD为平行四边形,
∵DF=BF,CE⊥BD,∴BC=CD=
解后反思 本题考查了平行四边形的判定和性质、三角形中位线定理、勾股定理,熟练掌握平行四边形的判定和性质定理是解题的关键.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
