9.3~9.5阶段巩固检测 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册
文档属性
| 名称 | 9.3~9.5阶段巩固检测 同步提优练习 (含答案)2024-2025学年苏科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 227.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.3~9.5阶段巩固检测
题型1 平行四边形
1.(2024·湖南中考)如图,在四边形ABCD 中,AB∥CD,点 E 在边AB 上, .请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 BCDE 为平行四边形;
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
题型2 菱形
2.(2024·扬州江都区一模)如图,在四边形ABCD 中,AB∥DC,AB=AD,对角线 AC、BD 交于点O,AC 平分∠BAD,过点 C 作CE⊥AB 交AB 的延长线于点E,连接OE.
(1)求证:四边形 ABCD 是菱形;
(2)若 求OE 的长.
题型3 矩形
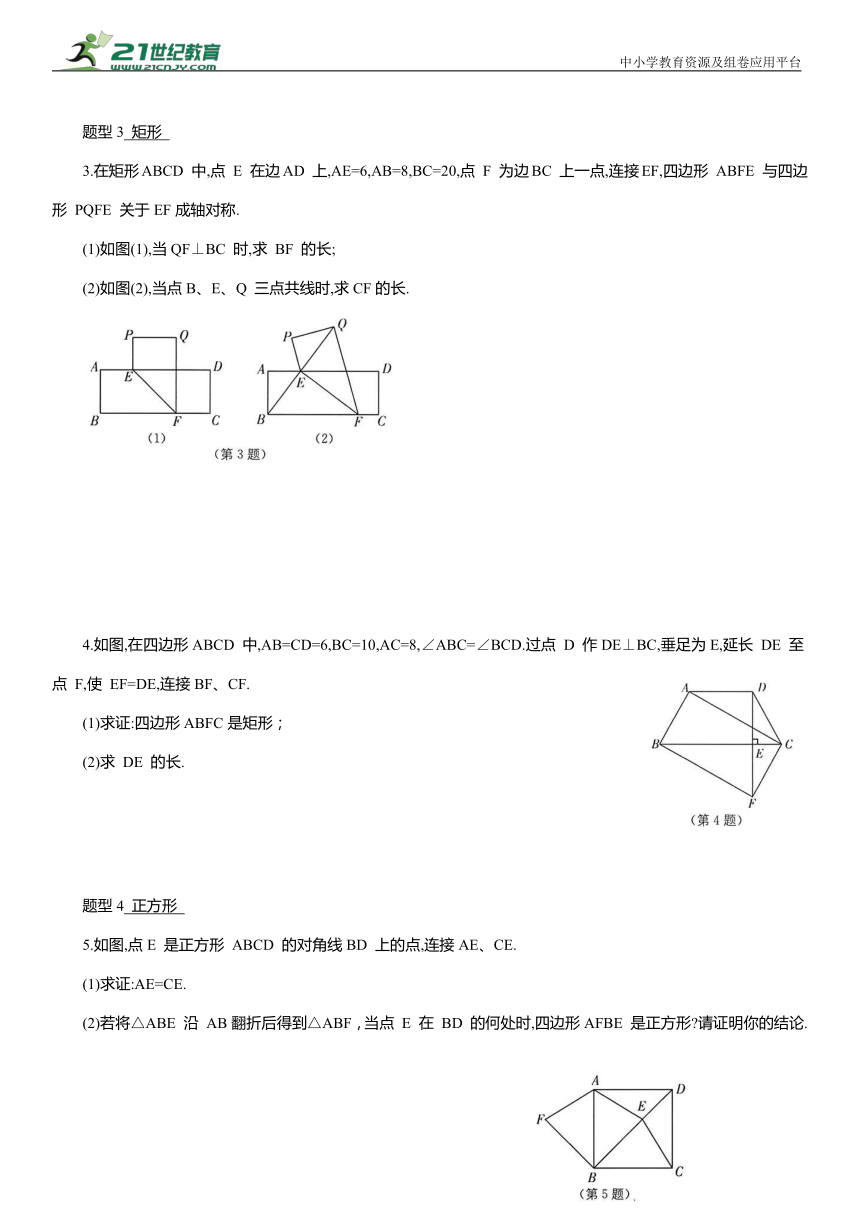
3.在矩形ABCD 中,点 E 在边AD 上,AE=6,AB=8,BC=20,点 F 为边BC 上一点,连接EF,四边形 ABFE 与四边形 PQFE 关于EF成轴对称.
(1)如图(1),当QF⊥BC 时,求 BF 的长;
(2)如图(2),当点B、E、Q 三点共线时,求CF的长.
4.如图,在四边形ABCD 中,AB=CD=6,BC=10,AC=8,∠ABC=∠BCD.过点 D 作DE⊥BC,垂足为E,延长 DE 至点 F,使 EF=DE,连接BF、CF.
(1)求证:四边形ABFC是矩形;
(2)求 DE 的长.
题型4 正方形
5.如图,点E 是正方形 ABCD 的对角线BD 上的点,连接AE、CE.
(1)求证:AE=CE.
(2)若将△ABE 沿 AB翻折后得到△ABF,当点 E 在 BD 的何处时,四边形AFBE 是正方形 请证明你的结论.
题型5 中位线定理
6.(2024·盐城东台期中)如图,BD、CE 分别为△ABC的中线,BD、CE 交于点G,点 M、N 分别是BG、CG 的中点.求证:
(1)EM∥DN;
(2)CG=2EG.
7.如图,在四边形ABCD中,AD∥BC,AB=4,BC=8,AD=6,∠B=90°,点M从点B 出发,以每秒 单位长度的速度沿 BC 向右运动,移动到点C时立即沿原路按原速返回,点N 从点D 出发,以每秒1个单位长度的速度沿线段 DA 向左运动. M、N两点同时出发,当点 N 运动到点A 时,M、N两点同时停止运动,设运动时间为t(秒).
(1)当t= 秒时,四边形 ABMN 为矩形;
(2)在整个运动过程中,t为何值时,以C、D、M、N为顶点的四边形为平行四边形
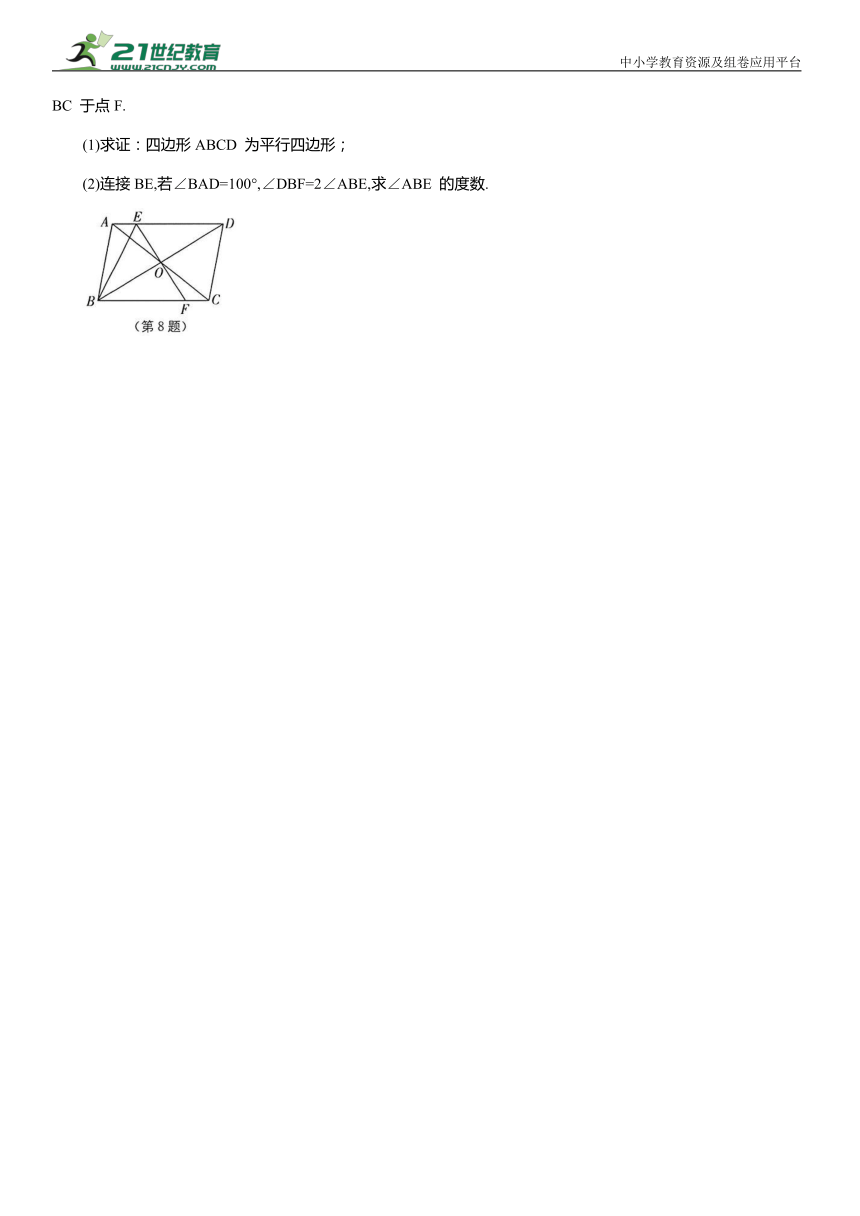
8.如图,在四边形ABCD 中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD 于点E,交 BC 于点F.
(1)求证:四边形ABCD 为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE 的度数.
阶段巩固检测(9.3~9.5)
1.(1)选择①,∵∠B=∠AED,∴BC∥DE.
∵AB∥CD,∴四边形 BCDE 为平行四边形.
选择②,∵AE=BE,AE=CD,∴BE=CD,∵AB∥CD,∴四边形 BCDE 为平行四边形.
(2)由(1)可知,四边形 BCDE 为平行四边形,
∴DE=BC=10.∵AD⊥AB,∴∠A=90°,
即线段AE 的长为6.
归纳总结 判定一个四边形是平行四边形的方法:
判定方法
边 两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
角 两组对角分别相等的四边形是平行四边形
对角 线 对角线互相平分的四边形是平行四边形
2.(1)∵AB∥DC,∴∠OAB=∠DCA.
∵AC为∠DAB 的平分线,∴∠OAB=∠DAC,
∴∠DCA=∠DAC,∴CD=AD=AB.
又AB∥DC,∴四边形ABCD 是平行四边形.
∵AD=AB,∴平行四边形ABCD 是菱形.
(2)∵四边形ABCD 是菱形,
∴OA=OC,BD⊥AC.
∵CE⊥AB,∴OE=OA=OC.
在Rt△AOB 中,AB= ,OB=1,
.
解后反思 本题主要考查了菱形的判定和性质,掌握平行四边形的判定和性质,角平分线的定义,勾股定理,判断出CD=AD=AB是解答本题的关键.
3.(1)设QF 与AD 相交于点G,
∵四边形ABCD 是矩形,
∴∠A=∠B=90°,AD∥BC.
∵QF⊥BC,∴QF⊥AD.
∵四边形 ABFE 与四边形 PQFE 关于 EF 成轴对称,
∴∠P=∠A=90°,∠Q=∠B=90°,PE=AE=6,PQ=AB=8,∴四边形ABFG、PEGQ都是矩形,
∴BF=AG,EG=PQ=8,
∴BF=AG=AE+EG=14.
(2)∵四边形 ABFE 与四边形 PQFE 关于EF 成轴对称,∴B、Q关于EF 成轴对称.
当B、E、Q三点共线时,∴∠BEF=∠QEF=90°.如图,过点 E作EM⊥BC于点M,
又∠A=∠ABC=90°,∴四边形ABME 是矩形,
∴BM=AE=6,EM=AB=8.
∵∠A=90°,AE=6,AB=8,
在Rt△BEF 中,
在 Rt△MEF 中,
又BC=20,∴CF=BC-BF=
4.(1)∵DE⊥BC,∴∠DEC=∠FEC=90°.在△DEC 和△FEC中
∴△DEC≌△FEC(SAS),∴CF=CD.
∵AB=CD,∴CF=AB.
同理BF=AC.∴四边形ABFC是平行四边形.
∵AB=6,BC=10,AC=8,
∴平行四边形ABFC 是矩形.
(2)如图,过点A 作AH⊥BC于点 H,
∴∠AHB=∠DEC=90°.
在△ABH 和△DCE 中.
∴△ABH≌△DCE(AAS),∴AH=DE.
∴DE=AH=4.8.
5.(1)∵四边形ABCD 是正方形,
∴AB=CB,∠ABE=∠CBE=45°.
在△ABE 和△CBE 中,
∴△ABE≌△CBE(SAS),
∴AE=CE.
(2)点E 在BD 的中点时,四边形AFBE 是正方形.理由如下:
由折叠的性质,得∠F=∠AEB,AF=AE,BF=BE,
∵∠BAD=90°,E 是BD的中点,
∵BF=BE,∴AE=BE=AF=BF,
∴四边形 AFBE 是菱形,E 是正方形ABCD 对角线的交点,∴AE⊥BD,∴∠AEB=90°,
∴四边形AFBE 是正方形.
6.(1)连接AG,
∵BD、CE 分别为△ABC 的中线,点 M、N 分别是BG、CG的中点,
∴AE=BE,BM=GM,AD=CD,CN=GN,
∴EM∥AG,DN∥AG,∴EM∥DN.
(2)由(1)知AE=BE,BM=GM,AD=CD,CN=GN
∵EM∥DN,∴∠MEG=∠DNG,∠EMG=∠NDG,
∴易证△EMG≌△NDG(ASA),
∴EG=GN,∴CG=2EG.
7.(1) [解析]∵AD∥BC,∠B=90°,
∴当AN=BM时,四边形ABMN 为矩形.
由题意知AN=AD-DN=6-t,
当点 M 从点 B 运动到点C时,
令 解得
当点M 从点C返回到点B时,
令 解得
当t=6时,点M、N停止运动,故 不符合题意,舍去,
秒时,四边形ABMN 为矩形.
(2)∵AD∥BC,
∴当DN=CM时,以C、D、M、N 为顶点的四边形为平行四边形,
由题意知DN=t,
当点 M 从点 B 运动到点C时, 令 解得
当点 M从点C返回到点B时, 令 解得
检验可知 和 均符合题意,
∴t为 或 时,以C、D、M、N为顶点的四边形为平行四边形.
8.(1)∵AD∥BC,∴∠OAD=∠OCB.
在△AOD 和△COB 中,
∴△AOD≌△COB(ASA),∴AD=CB.
又AD∥BC,∴四边形ABCD为平行四边形.
(2)设∠ABE=x,则∠DBF=2x.
由(1),得四边形ABCD 为平行四边形,∴OB=OD.
∵EF⊥BD,∴BE=DE,∴∠EBD=∠EDB.
∵AD∥BC,∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x.
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
解得x=16°,即
9.3~9.5阶段巩固检测
题型1 平行四边形
1.(2024·湖南中考)如图,在四边形ABCD 中,AB∥CD,点 E 在边AB 上, .请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 BCDE 为平行四边形;
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
题型2 菱形
2.(2024·扬州江都区一模)如图,在四边形ABCD 中,AB∥DC,AB=AD,对角线 AC、BD 交于点O,AC 平分∠BAD,过点 C 作CE⊥AB 交AB 的延长线于点E,连接OE.
(1)求证:四边形 ABCD 是菱形;
(2)若 求OE 的长.
题型3 矩形
3.在矩形ABCD 中,点 E 在边AD 上,AE=6,AB=8,BC=20,点 F 为边BC 上一点,连接EF,四边形 ABFE 与四边形 PQFE 关于EF成轴对称.
(1)如图(1),当QF⊥BC 时,求 BF 的长;
(2)如图(2),当点B、E、Q 三点共线时,求CF的长.
4.如图,在四边形ABCD 中,AB=CD=6,BC=10,AC=8,∠ABC=∠BCD.过点 D 作DE⊥BC,垂足为E,延长 DE 至点 F,使 EF=DE,连接BF、CF.
(1)求证:四边形ABFC是矩形;
(2)求 DE 的长.
题型4 正方形
5.如图,点E 是正方形 ABCD 的对角线BD 上的点,连接AE、CE.
(1)求证:AE=CE.
(2)若将△ABE 沿 AB翻折后得到△ABF,当点 E 在 BD 的何处时,四边形AFBE 是正方形 请证明你的结论.
题型5 中位线定理
6.(2024·盐城东台期中)如图,BD、CE 分别为△ABC的中线,BD、CE 交于点G,点 M、N 分别是BG、CG 的中点.求证:
(1)EM∥DN;
(2)CG=2EG.
7.如图,在四边形ABCD中,AD∥BC,AB=4,BC=8,AD=6,∠B=90°,点M从点B 出发,以每秒 单位长度的速度沿 BC 向右运动,移动到点C时立即沿原路按原速返回,点N 从点D 出发,以每秒1个单位长度的速度沿线段 DA 向左运动. M、N两点同时出发,当点 N 运动到点A 时,M、N两点同时停止运动,设运动时间为t(秒).
(1)当t= 秒时,四边形 ABMN 为矩形;
(2)在整个运动过程中,t为何值时,以C、D、M、N为顶点的四边形为平行四边形
8.如图,在四边形ABCD 中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD 于点E,交 BC 于点F.
(1)求证:四边形ABCD 为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE 的度数.
阶段巩固检测(9.3~9.5)
1.(1)选择①,∵∠B=∠AED,∴BC∥DE.
∵AB∥CD,∴四边形 BCDE 为平行四边形.
选择②,∵AE=BE,AE=CD,∴BE=CD,∵AB∥CD,∴四边形 BCDE 为平行四边形.
(2)由(1)可知,四边形 BCDE 为平行四边形,
∴DE=BC=10.∵AD⊥AB,∴∠A=90°,
即线段AE 的长为6.
归纳总结 判定一个四边形是平行四边形的方法:
判定方法
边 两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
角 两组对角分别相等的四边形是平行四边形
对角 线 对角线互相平分的四边形是平行四边形
2.(1)∵AB∥DC,∴∠OAB=∠DCA.
∵AC为∠DAB 的平分线,∴∠OAB=∠DAC,
∴∠DCA=∠DAC,∴CD=AD=AB.
又AB∥DC,∴四边形ABCD 是平行四边形.
∵AD=AB,∴平行四边形ABCD 是菱形.
(2)∵四边形ABCD 是菱形,
∴OA=OC,BD⊥AC.
∵CE⊥AB,∴OE=OA=OC.
在Rt△AOB 中,AB= ,OB=1,
.
解后反思 本题主要考查了菱形的判定和性质,掌握平行四边形的判定和性质,角平分线的定义,勾股定理,判断出CD=AD=AB是解答本题的关键.
3.(1)设QF 与AD 相交于点G,
∵四边形ABCD 是矩形,
∴∠A=∠B=90°,AD∥BC.
∵QF⊥BC,∴QF⊥AD.
∵四边形 ABFE 与四边形 PQFE 关于 EF 成轴对称,
∴∠P=∠A=90°,∠Q=∠B=90°,PE=AE=6,PQ=AB=8,∴四边形ABFG、PEGQ都是矩形,
∴BF=AG,EG=PQ=8,
∴BF=AG=AE+EG=14.
(2)∵四边形 ABFE 与四边形 PQFE 关于EF 成轴对称,∴B、Q关于EF 成轴对称.
当B、E、Q三点共线时,∴∠BEF=∠QEF=90°.如图,过点 E作EM⊥BC于点M,
又∠A=∠ABC=90°,∴四边形ABME 是矩形,
∴BM=AE=6,EM=AB=8.
∵∠A=90°,AE=6,AB=8,
在Rt△BEF 中,
在 Rt△MEF 中,
又BC=20,∴CF=BC-BF=
4.(1)∵DE⊥BC,∴∠DEC=∠FEC=90°.在△DEC 和△FEC中
∴△DEC≌△FEC(SAS),∴CF=CD.
∵AB=CD,∴CF=AB.
同理BF=AC.∴四边形ABFC是平行四边形.
∵AB=6,BC=10,AC=8,
∴平行四边形ABFC 是矩形.
(2)如图,过点A 作AH⊥BC于点 H,
∴∠AHB=∠DEC=90°.
在△ABH 和△DCE 中.
∴△ABH≌△DCE(AAS),∴AH=DE.
∴DE=AH=4.8.
5.(1)∵四边形ABCD 是正方形,
∴AB=CB,∠ABE=∠CBE=45°.
在△ABE 和△CBE 中,
∴△ABE≌△CBE(SAS),
∴AE=CE.
(2)点E 在BD 的中点时,四边形AFBE 是正方形.理由如下:
由折叠的性质,得∠F=∠AEB,AF=AE,BF=BE,
∵∠BAD=90°,E 是BD的中点,
∵BF=BE,∴AE=BE=AF=BF,
∴四边形 AFBE 是菱形,E 是正方形ABCD 对角线的交点,∴AE⊥BD,∴∠AEB=90°,
∴四边形AFBE 是正方形.
6.(1)连接AG,
∵BD、CE 分别为△ABC 的中线,点 M、N 分别是BG、CG的中点,
∴AE=BE,BM=GM,AD=CD,CN=GN,
∴EM∥AG,DN∥AG,∴EM∥DN.
(2)由(1)知AE=BE,BM=GM,AD=CD,CN=GN
∵EM∥DN,∴∠MEG=∠DNG,∠EMG=∠NDG,
∴易证△EMG≌△NDG(ASA),
∴EG=GN,∴CG=2EG.
7.(1) [解析]∵AD∥BC,∠B=90°,
∴当AN=BM时,四边形ABMN 为矩形.
由题意知AN=AD-DN=6-t,
当点 M 从点 B 运动到点C时,
令 解得
当点M 从点C返回到点B时,
令 解得
当t=6时,点M、N停止运动,故 不符合题意,舍去,
秒时,四边形ABMN 为矩形.
(2)∵AD∥BC,
∴当DN=CM时,以C、D、M、N 为顶点的四边形为平行四边形,
由题意知DN=t,
当点 M 从点 B 运动到点C时, 令 解得
当点 M从点C返回到点B时, 令 解得
检验可知 和 均符合题意,
∴t为 或 时,以C、D、M、N为顶点的四边形为平行四边形.
8.(1)∵AD∥BC,∴∠OAD=∠OCB.
在△AOD 和△COB 中,
∴△AOD≌△COB(ASA),∴AD=CB.
又AD∥BC,∴四边形ABCD为平行四边形.
(2)设∠ABE=x,则∠DBF=2x.
由(1),得四边形ABCD 为平行四边形,∴OB=OD.
∵EF⊥BD,∴BE=DE,∴∠EBD=∠EDB.
∵AD∥BC,∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x.
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
解得x=16°,即
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
