九年级数学上册人教版 24.1.3 《弧、弦、圆心角》课时练习(含答案)
文档属性
| 名称 | 九年级数学上册人教版 24.1.3 《弧、弦、圆心角》课时练习(含答案) | 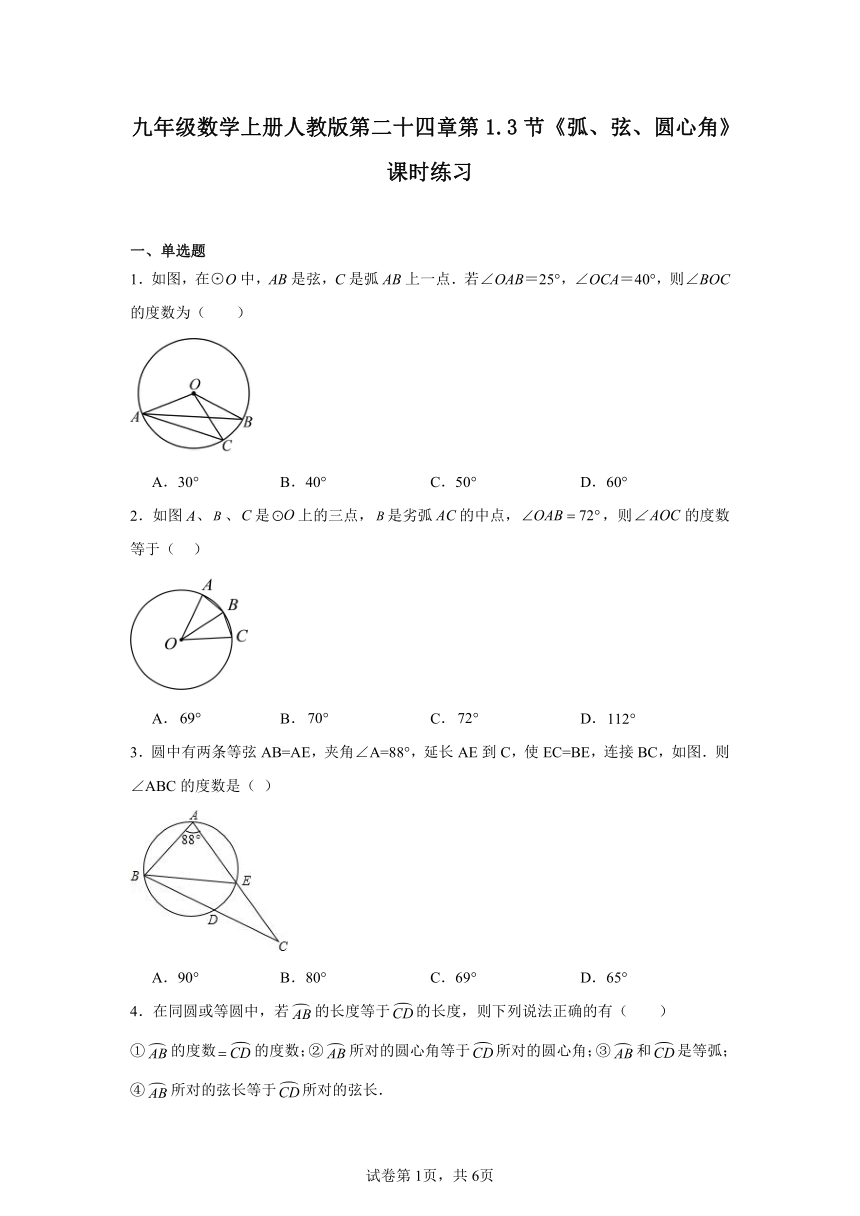 | |
| 格式 | docx | ||
| 文件大小 | 1011.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 07:53:26 | ||
图片预览



文档简介
九年级数学上册人教版第二十四章第1.3节《弧、弦、圆心角》课时练习
一、单选题
1.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
2.如图A、、是上的三点,是劣弧的中点,,则的度数等于( )
A. B. C. D.
3.圆中有两条等弦AB=AE,夹角∠A=88°,延长AE到C,使EC=BE,连接BC,如图.则∠ABC的度数是( )
A.90° B.80° C.69° D.65°
4.在同圆或等圆中,若的长度等于的长度,则下列说法正确的有( )
①的度数的度数;②所对的圆心角等于所对的圆心角;③和是等弧;④所对的弦长等于所对的弦长.
A.1个 B.2个 C.3个 D.4个
5.如图,在中,,是两条弦,,,如果,则下列结论不正确的是( )
A. B.
C. D.
6.如图1为某酒店的圆形旋转门,可看成如图2由外围的和3翼隔风玻璃组成,外围圆有通道和,且它们关于圆心中心对称,圆内的3翼隔风玻璃可绕圆心转动,且所成的夹角,3翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内保温作用.例如:当隔风玻璃转到如图2位置时,大厅内外空气被隔风玻璃,隔离.则通道所对圆心角的度数的最大值为( )
A.30° B.60° C.90° D.120°
7.如图,已知:是的直径,、是上的三等分点,,则是( )
A. B. C. D.
8.如图所示,在中,,则在①;②;③;④中,正确结论的个数是( )
A.1 B.2 C.3 D.4
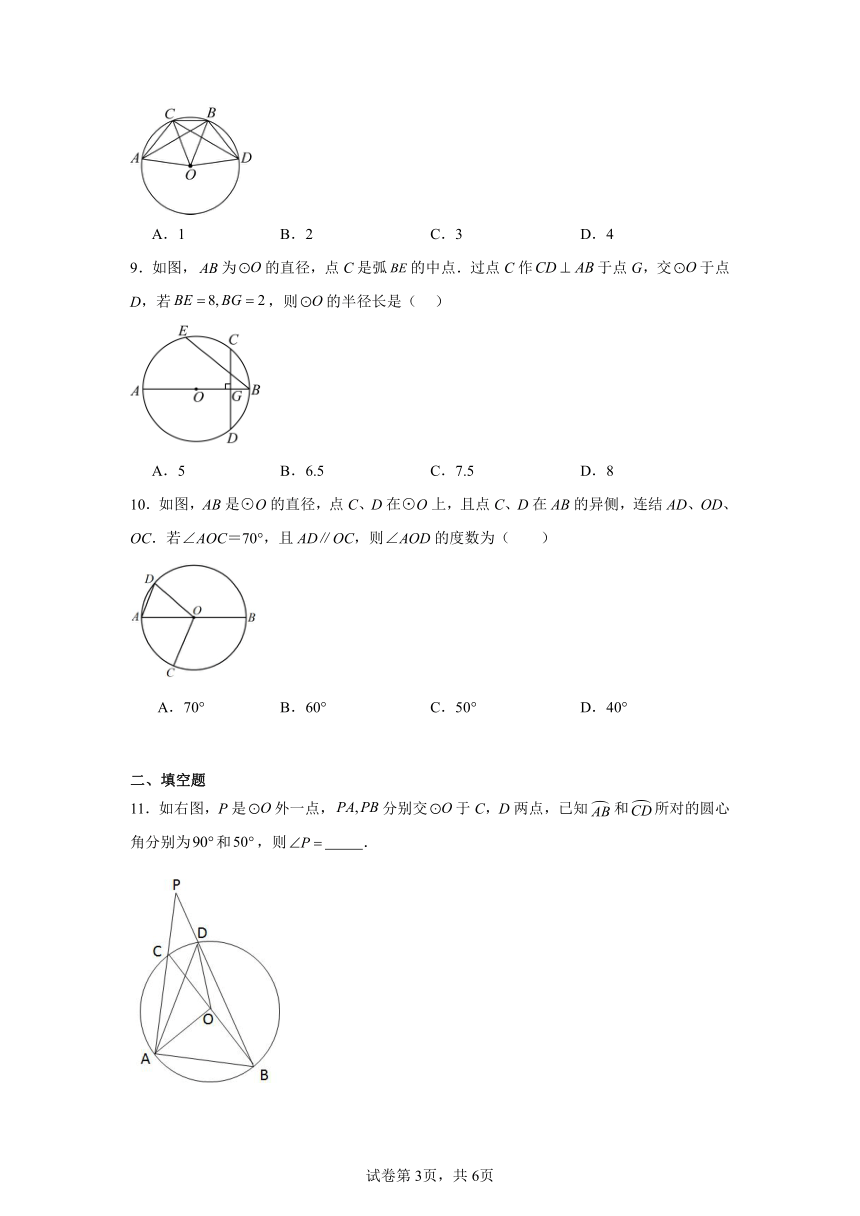
9.如图,为的直径,点C是弧的中点.过点C作于点G,交于点D,若,则的半径长是( )
A.5 B.6.5 C.7.5 D.8
10.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
二、填空题
11.如右图,P是外一点,分别交于C,D两点,已知和所对的圆心角分别为和,则 .
12.如图,一把三角尺,,.将其放置在量角器上,点O与圆心重合,若三角尺的直角边和量角器所在圆的半径相等,点C是斜边与量角器边缘的交点,若B点的对应刻度为,则C点的对应刻度为 .
13.如图,⊙O1的半径是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,若的度数是48°,那么的度数是 .
14.如图,点,点,点在上,分别连接,,.若,,则 .
15.如图,已知为的直径,为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角 .
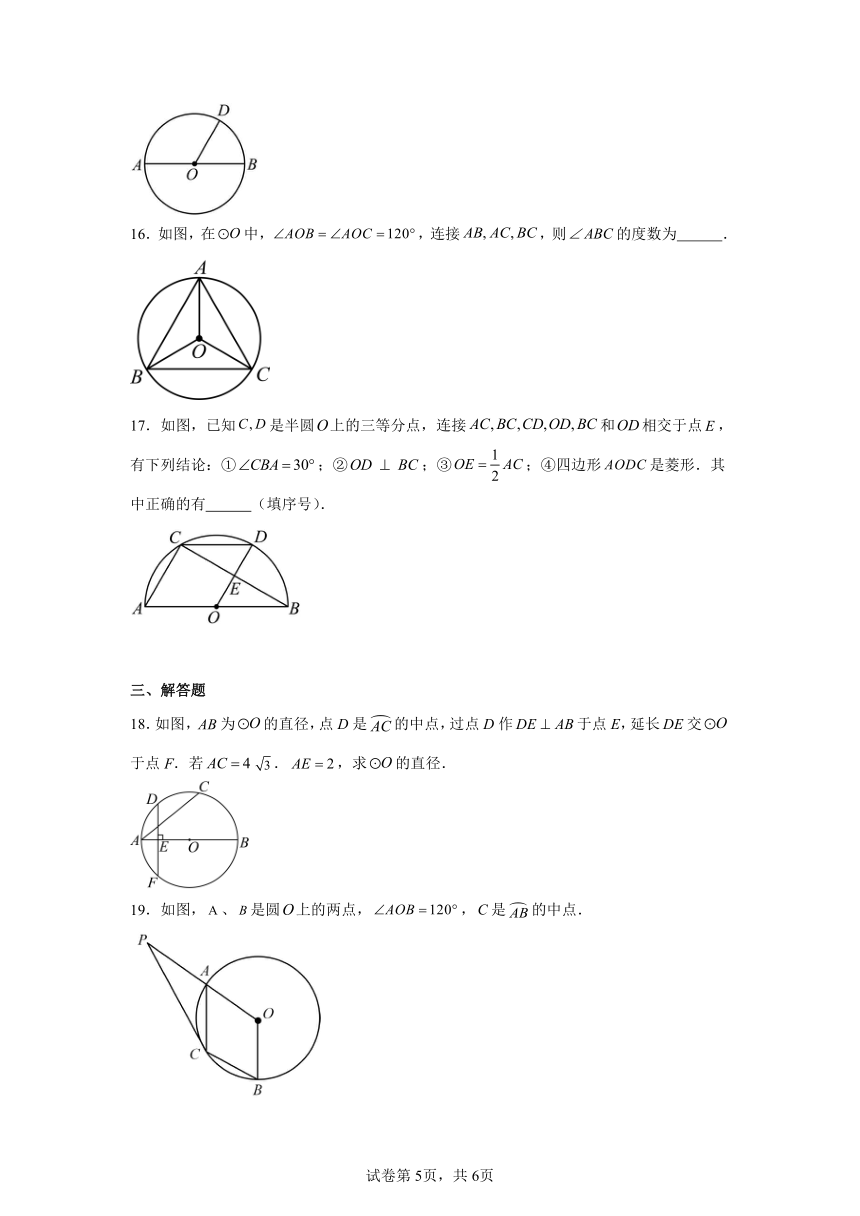
16.如图,在中,,连接,则的度数为 .
17.如图,已知是半圆上的三等分点,连接和相交于点,有下列结论:①;②;③;④四边形是菱形.其中正确的有 (填序号).
三、解答题
18.如图,为的直径,点D是的中点,过点D作于点E,延长交于点F.若.,求的直径.
19.如图,、是圆上的两点,,是的中点.
(1)求证:平分;
(2)延长至,使得,连接,若圆的半径,求的长.
20.如图,在中,弦相交于点E,连接,已知.
(1)求证:;
(2)如果的半径为5,,求的长.
21.如图,A、B是上的两个点,连接、点C,D是、上靠近圆心O的三等分点,点E、F是的三等分点,连接,,
(1)求证:
(2)连接,,请你判断,的位置关系,并说明理由.
22.如图,在中,C,D是直径上的两点,且,交于C、D,点E,G,F,H在上.
(1)若,求半径;
(2)求证:;
(3)若C,D分别为的中点,则成立吗?请说明理由.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章第1.3节《弧、弦、圆心角》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D C B C D A D
11.20°
12./82度
13.24°
14./20度
15.60
16./60度
17.解:连接,
∵已知是半圆上的三等分点,
∴,
∴,故①正确;
∴,
∴,故②正确;
∴,,
∴是的中位线,
∴,故③正确;
∵是半圆O的直径,
∴,又,
∴,
∵,,
∴是等边三角形,
∴,
∴四边形是平行四边形,又,
∴四边形是菱形.故④正确,
故答案为:①②③④.
18.解:如图,连接,
∵,
∴,
∵点D是弧的中点,
∴
∴,
∴,
∴
设,
∵,
∴
∴,
∴的直径.
故答案为:
19.(1)证明:连接、,
∵,是弧的中点,
∴,
∵,
∴是等边三角形,
∴,同理,
∴,
∴四边形是菱形,
∴平分;
(2)解:∵是等边三角形,
∴,,
又∵,
∴,
∴,
∴,
∴是直角三角形,
∵,,
∴.
20.(1)证明:∵,
∴,
在与中,
,
∴,
∴;
(2)解:过O作与F,于G,连接,则,
∴四边形是矩形,
根据垂径定理得:,
∵,
∴,
在与中,
,
∴,
∴,
∵,
∴四边形是正方形,
∴,
设,则,
∴,
即,
解得:或(舍去),
∴,
∴.
21.(1)证明:连接、,则,
∵C、D为、三等分点,
∴,
∵E、F为的三等分点,
∴,
∴,
∴,
∴;
(2)解:.理由如下:
取的中点M,连接,则,
∴,,
∴,
∵为等腰三角形,,
∴,
∴.
22.(1)如图1,连接,
设半径为r,
∵,
∴.
∵,
∴,
在中,,
∴,
解得,
∴半径为5;
(2)如图1,在(1)基础上连接,
∵,
∴.
∵,
∴在和中,,
∴,
∴,
∴;
(3)成立,理由如下:
∵C,D分别为的中点,
∴,
∴
∴,
同理,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
2.如图A、、是上的三点,是劣弧的中点,,则的度数等于( )
A. B. C. D.
3.圆中有两条等弦AB=AE,夹角∠A=88°,延长AE到C,使EC=BE,连接BC,如图.则∠ABC的度数是( )
A.90° B.80° C.69° D.65°
4.在同圆或等圆中,若的长度等于的长度,则下列说法正确的有( )
①的度数的度数;②所对的圆心角等于所对的圆心角;③和是等弧;④所对的弦长等于所对的弦长.
A.1个 B.2个 C.3个 D.4个
5.如图,在中,,是两条弦,,,如果,则下列结论不正确的是( )
A. B.
C. D.
6.如图1为某酒店的圆形旋转门,可看成如图2由外围的和3翼隔风玻璃组成,外围圆有通道和,且它们关于圆心中心对称,圆内的3翼隔风玻璃可绕圆心转动,且所成的夹角,3翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内保温作用.例如:当隔风玻璃转到如图2位置时,大厅内外空气被隔风玻璃,隔离.则通道所对圆心角的度数的最大值为( )
A.30° B.60° C.90° D.120°
7.如图,已知:是的直径,、是上的三等分点,,则是( )
A. B. C. D.
8.如图所示,在中,,则在①;②;③;④中,正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,为的直径,点C是弧的中点.过点C作于点G,交于点D,若,则的半径长是( )
A.5 B.6.5 C.7.5 D.8
10.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
二、填空题
11.如右图,P是外一点,分别交于C,D两点,已知和所对的圆心角分别为和,则 .
12.如图,一把三角尺,,.将其放置在量角器上,点O与圆心重合,若三角尺的直角边和量角器所在圆的半径相等,点C是斜边与量角器边缘的交点,若B点的对应刻度为,则C点的对应刻度为 .
13.如图,⊙O1的半径是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,若的度数是48°,那么的度数是 .
14.如图,点,点,点在上,分别连接,,.若,,则 .
15.如图,已知为的直径,为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角 .
16.如图,在中,,连接,则的度数为 .
17.如图,已知是半圆上的三等分点,连接和相交于点,有下列结论:①;②;③;④四边形是菱形.其中正确的有 (填序号).
三、解答题
18.如图,为的直径,点D是的中点,过点D作于点E,延长交于点F.若.,求的直径.
19.如图,、是圆上的两点,,是的中点.
(1)求证:平分;
(2)延长至,使得,连接,若圆的半径,求的长.
20.如图,在中,弦相交于点E,连接,已知.
(1)求证:;
(2)如果的半径为5,,求的长.
21.如图,A、B是上的两个点,连接、点C,D是、上靠近圆心O的三等分点,点E、F是的三等分点,连接,,
(1)求证:
(2)连接,,请你判断,的位置关系,并说明理由.
22.如图,在中,C,D是直径上的两点,且,交于C、D,点E,G,F,H在上.
(1)若,求半径;
(2)求证:;
(3)若C,D分别为的中点,则成立吗?请说明理由.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章第1.3节《弧、弦、圆心角》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D C B C D A D
11.20°
12./82度
13.24°
14./20度
15.60
16./60度
17.解:连接,
∵已知是半圆上的三等分点,
∴,
∴,故①正确;
∴,
∴,故②正确;
∴,,
∴是的中位线,
∴,故③正确;
∵是半圆O的直径,
∴,又,
∴,
∵,,
∴是等边三角形,
∴,
∴四边形是平行四边形,又,
∴四边形是菱形.故④正确,
故答案为:①②③④.
18.解:如图,连接,
∵,
∴,
∵点D是弧的中点,
∴
∴,
∴,
∴
设,
∵,
∴
∴,
∴的直径.
故答案为:
19.(1)证明:连接、,
∵,是弧的中点,
∴,
∵,
∴是等边三角形,
∴,同理,
∴,
∴四边形是菱形,
∴平分;
(2)解:∵是等边三角形,
∴,,
又∵,
∴,
∴,
∴,
∴是直角三角形,
∵,,
∴.
20.(1)证明:∵,
∴,
在与中,
,
∴,
∴;
(2)解:过O作与F,于G,连接,则,
∴四边形是矩形,
根据垂径定理得:,
∵,
∴,
在与中,
,
∴,
∴,
∵,
∴四边形是正方形,
∴,
设,则,
∴,
即,
解得:或(舍去),
∴,
∴.
21.(1)证明:连接、,则,
∵C、D为、三等分点,
∴,
∵E、F为的三等分点,
∴,
∴,
∴,
∴;
(2)解:.理由如下:
取的中点M,连接,则,
∴,,
∴,
∵为等腰三角形,,
∴,
∴.
22.(1)如图1,连接,
设半径为r,
∵,
∴.
∵,
∴,
在中,,
∴,
解得,
∴半径为5;
(2)如图1,在(1)基础上连接,
∵,
∴.
∵,
∴在和中,,
∴,
∴,
∴;
(3)成立,理由如下:
∵C,D分别为的中点,
∴,
∴
∴,
同理,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
