由样本所占百分比估计总体的数量综合题典型题型 归纳练 2025年中考数学二轮复习备考
文档属性
| 名称 | 由样本所占百分比估计总体的数量综合题典型题型 归纳练 2025年中考数学二轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 16:59:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
由样本所占百分比估计总体的数量综合题典型题型
归纳练 2025年中考数学二轮复习备考
一、解答题
1.为丰富学生业余活动,某中学决定再增加四种选修课,分别是:.青春舌战辩论;.时政瞭望;.美食与地理;.动漫创作,为了解学生喜好,在全校七年级范围内展开抽样问卷调查每位被调查的同学必须选择且只能选择一种,将数据进行整理后绘制成如下两幅不完整的统计图.
请根据上述信息,解答下列问题:
(1)这次一共调查了______名学生,并补全条形统计图;
(2)求扇形统计图中所对应的扇形的圆心角度数;
(3)若该地区七年级学生共有人,估计该地区七年级学生中喜欢“动漫创作”的学生有多少人?
2.某学校为了掌握中考复习状况,对会考指导讲解阶段学生课堂参与的深度和广度进行调查,其项目为:主动质疑、独立思考、专注听讲、能为他人讲解题目四项.调查组随机抽取了若干名九年级学生的课堂参与情况,获得了初步数据如下:
主动质疑:80人,独立思考120人,专注听讲160人,能为他人讲题学生若干,绘制了如下图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)这次评价中一共抽查了_____名学生;
(2)请将条形统计图补充完整;
(3)若全校有2000名九年级学生,请估计在复习后期模拟试卷讲评课中,“主动质疑”的学生约有多少人?
3.某校组织全体学生参加一次大型知识竞赛,从中随机抽取部分学生的竞赛成绩组成一个样本.所有学生的竞赛成绩分为四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.现根据抽取的学生的竞赛成绩绘制了如下两幅不完整的统计图.请你根据信息,解答下列问题:
抽取的学生的竞赛成绩条形统计图
抽取的学生的竞赛成绩扇形统计图
(1)在抽取的样本中,等级、等级的各有多少人?请把条形统计图补充完整.
(2)在扇形统计图中,求等级所对应的圆心角的度数.
(3)若知识竞赛成绩等级为优秀,请你估计该校参加竞赛的1500名学生中成绩优秀的人数.
4.学校为了响应国家“五育并举”的号召,增强学生体质,计划开展阳光体育锻炼活动.学校准备开设以下四个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),要求每位学生必须参加,且只能选择其中一项,并将选择项目的抽样调查结果绘制成如下不完整的统计图,请你结合图中信息解答下列问题:
(1)本次调查的学生人数是______人;
(2)在扇形统计图中,B对应的圆心角为______度;
(3)已知该学校共有2000名学生,请根据样本估计全校选择篮球的人数是多少?
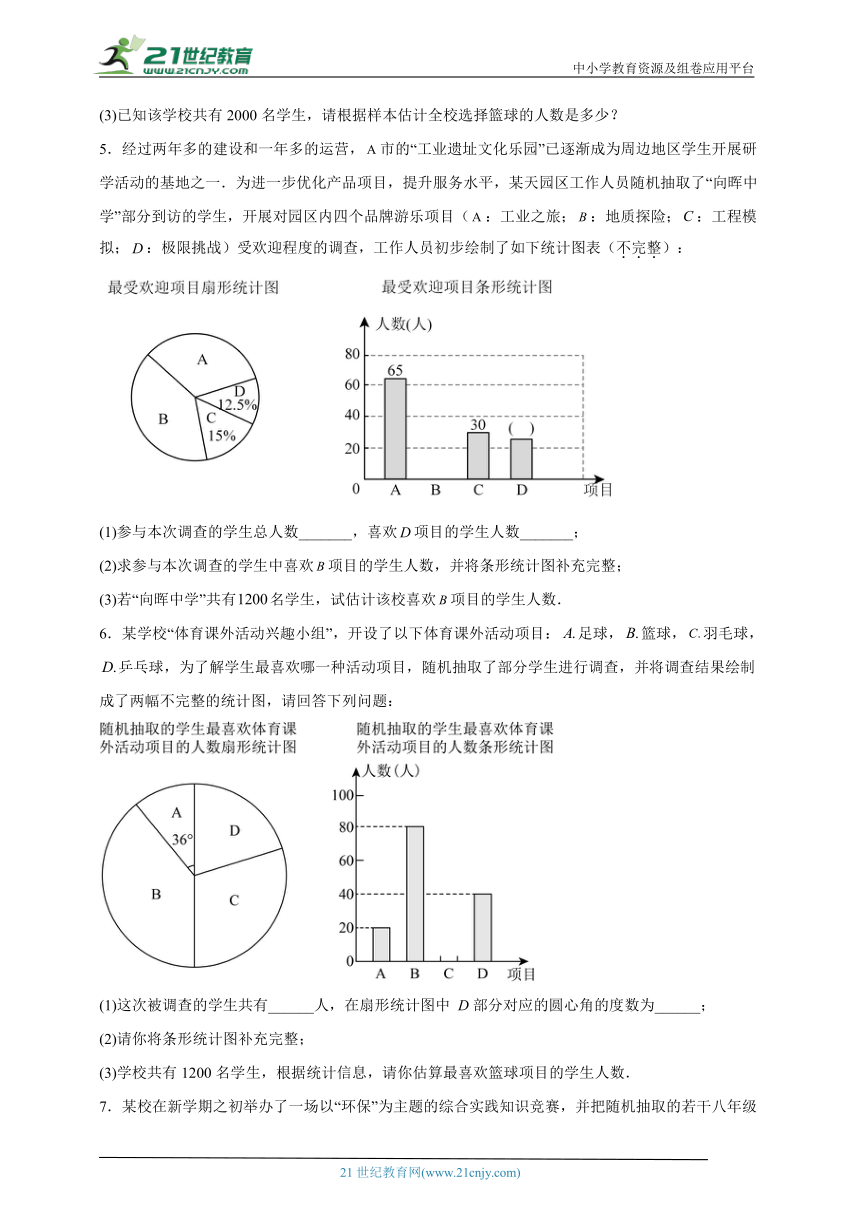
5.经过两年多的建设和一年多的运营,市的“工业遗址文化乐园”已逐渐成为周边地区学生开展研学活动的基地之一.为进一步优化产品项目,提升服务水平,某天园区工作人员随机抽取了“向晖中学”部分到访的学生,开展对园区内四个品牌游乐项目(:工业之旅;:地质探险;:工程模拟;:极限挑战)受欢迎程度的调查,工作人员初步绘制了如下统计图表(不完整):
(1)参与本次调查的学生总人数_______,喜欢项目的学生人数_______;
(2)求参与本次调查的学生中喜欢项目的学生人数,并将条形统计图补充完整;
(3)若“向晖中学”共有名学生,试估计该校喜欢项目的学生人数.
6.某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:足球,篮球,羽毛球,乒乓球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有______人,在扇形统计图中 D部分对应的圆心角的度数为______;
(2)请你将条形统计图补充完整;
(3)学校共有1200名学生,根据统计信息,请你估算最喜欢篮球项目的学生人数.
7.某校在新学期之初举办了一场以“环保”为主题的综合实践知识竞赛,并把随机抽取的若干八年级学生的竞赛成绩进行整理,绘制成如下不完整的统计表和统计图.
组别 成绩(分) 频数
A 2
B a
C 14
D b
E 10
(1)写出a,b的值,并补全频数直方图.
(2)求扇形统计图中,A组所对应的圆心角度数.
(3)该校八年级共有480人,根据统计信息,估计该校八年级学生的竞赛成绩在D组的人数.
8.某学校开展了以“红色文化”为主题的研学活动,为了解学生参与情况,随机抽取部分学生对研学活动时长(用表示,单位:)进行调查.经过整理,将数据分成四组(组:;组:;组:;组:,并绘制了如下不完整的条形统计图和扇形统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了_____名学生;
(2)补全条形统计图;
(3)扇形统计图中,组对应的扇形圆心角的度数是_____;
(4)若该学校共有学生名,请估计该校研学活动时长为的学生人数.
9.某校为了解学生的数学素养,随机抽取100名学生进行模拟测试(每位学员答5道数学题,其中答对4道及以上为优秀),经过两周训练,对这些学生进行第二次模拟测试,将这两次模拟成绩进行整理、分析,并制作成如下统计表.
(1)在扇形统计图中,“答对4道”所在扇形的圆心角为________度.
(2)若该校有1200名学生,估计第一次模拟测试达到“优秀”的学生人数.
(3)你认为学生的两周训练是否有效?请用相关统计量说明理由.
10.某校为丰富学生的课余生活,开展了多姿多彩的体育活动,开设了五种球类运动项目:A篮球,B足球,C排球,D羽毛球,E乒乓球.为了解学生最喜欢以上哪种球类运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并绘制了统计图.某同学不小心将图中部分数据丢失,请结合统计图,完成下列问题:
(1)本次随机抽取多少名学生进行调查?并补全条形统计图;
(2)求扇形统计图中C对应圆心角的度数;
(3)若该校共有2000名学生,请你估计该校最喜欢“E乒乓球”的学生人数.
参考答案
1.(1),作图见解析
(2)
(3)人
本题考查条形统计图和扇形统计图的关联、求扇形统计图中扇形的圆心角的度数、用样本估计总体,理解题意,能从统计图中获取有用信息是解答的关键.
(1)用喜欢选修课A的学生人数除以其所占的百分比调查总人数,进而求得喜欢选修课C的学生人数,然后补全条形统计图即可;
(2)用乘以所占的百分比即可求解;
(3)用学生总人数乘以样本中喜欢“动漫创作”的学生所占比例即可求解.
(1)解:调查总数为名,
喜欢“美食与地理”的人数为(名),
补全条形统计图如图所示:
故答案为:800;
(2)解:,
答:所对应的扇形的圆心角度数为;
(3)解:人,
答:估计该地区七年级学生中喜欢“动漫创作”的学生有人.
2.(1)400
(2)见解析
(3)400人
本题考查了条形统计图与扇形统计图信息相关联,用样本估计总体数量等知识,从统计图中获取必要的信息是解题的关键.
(1)根据专注听讲的人数及其所占的百分数,可求得抽查的学生人数;
(2)抽查的总人数分别减去主动质疑、独立思考、专注听讲的人数,求得讲解题目的人数,从而可补充条形统计图;
(3)主动质疑学生人数所占的百分比与全校九年级学生人数的乘积,即为所求.
(1)解:由题意知,抽查的学生人数为:(名)
故答案为:400;
(2)解:讲解题目的人数为:(人),
补充条形统计图如下:
(3)解:(人)
答:在复习后期模拟试卷讲评课中,“主动质疑”的学生约有400人.
3.(1)等级有50人,等级有40人,图见解析
(2)
(3)375名
本题主要考查了条形统计图和扇形统计图的关联,用样本估计总体,求扇形统计图中的圆心角的度数,熟练掌握以上知识是解题的关键.
(1)根据B组人数除以B组所占的百分比即可求出抽取的学生总人数,进而求得等级、等级的人数即可;
(2)先求出D级人数所占的百分比,再利用乘以这个百分比,即可求出D级对应扇形的圆心角的度数.
(3)根据总人数乘以成绩优秀学生所占的百分比即可求出本次竞赛的学生中成绩为优秀的学生人数.
(1)解:共抽取总人数为(人),
则等级人数为(人),
等级人数为(人),
补全条形统计图如图所示:
(2)解:等级所对应的圆心角的度数为;
(3)解:(名),
答:估计该校参加竞赛的1500名学生中成绩优秀的人数为375名.
4.(1)100
(2)
(3)520
本题主要考查了条形统计图和扇形统计图的综合运用、用样本估计整体等知识点读懂统计图,从不同的统计图中得到必要的信息是解题的关键,
(1)直接利用排球的人数除以其所占百分比即可求得总人数;
(2)用总人数减去A、C、D的人数求出选择乒乓球的人数,然后利用乘B的人数所占的比例即可;
(4)用总人数乘以选择篮球的人数所占的比例即可解答.
(1)解:本次调查的学生人数是(人).
故答案为:100.
(2)解:本次调查的学生中选择B(乒乓球)的人数为(人),
在扇形统计图中,B对应的圆心角为.
故答案为:.
(3)解:(人),
答:估计全校选择篮球的人数是520人.
5.(1),
(2)补图见解析
(3)名
()用项目学生人数除以其百分比可求出本次调查的学生总人数,进而可求出喜欢项目的学生人数;
()求出参与本次调查的学生中喜欢项目的学生人数,进而补全条形统计图即可;
()用乘以喜欢项目的学生人数占比即可求解;
本题考查了扇形统计图和条形统计图,样本估计总体,看懂统计图是解题的关键.
(1)解:参与本次调查的学生总人数为,
喜欢项目的学生人数为,
故答案为:,;
(2)解:参与本次调查的学生中喜欢项目的学生人数为,
∴将条形统计图补充完整如下:
(3)解:,
答:估计该校喜欢项目的学生人数为名.
6.(1)200,
(2)见解析
(3)480人
本题考查的是条形统计图和扇形统计图的综合运用,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)利用扇形统计图得到A类的百分比为,则用A类的频数除以可得到样本容量;然后用D类的百分比乘以得到在扇形统计图中“D”对应的圆心角的度数;
(2)先计算出C类的频数,然后补全统计图;
(3)利用总人数乘以对应的比例即可求解.
(1)解:(人),
所以这次被调查的学生共有200人,
在扇形统计图中“D”对应的圆心角的度数;
故答案为:200,;
(2)解:类人数为(人),
完整条形统计图为:
(3)解:(人),
答:估算最喜欢篮球项目的学生人数为480人.
7.(1),见解析;
(2)
(3)192人
本题考查频数分布表、扇形统计图、条形统计图、样本估计总体,解题的关键是从频数分布表和扇形统计图中获取关键信息.
(1)根据E组频数及所占百分数求出班级的总人数,进而可求出a、b;根据求出的a、b补全即可;
(2)先求出本次调查中A组的占比,再与360°相乘,即可作答;
(3)本次调查中八年级中分数在D组的占比与480相乘,即可作答.
(1)解:班级总人数为:,
∴
,
补全条形统计图如下:
(2)解:,
∴A组对应的圆心角的度数为;
(3)解:(人),
∴估计八年级中分数在D组的人数为192人.
8.(1);
(2)补全统计图见解析;
(3);
(4)估计该校研学活动时长为的学生人数有名.
本题考查了条形统计图,扇形统计图,圆心角,用样本估计总体,解题的关键在于对知识的熟练掌握与灵活运用.
()用“”组的人数除以所占比例即可得出答案;
()先求出“”组的人数,然后利用总人数减去,,组人数,即可补全条形统计图;
()用乘以“”所占的比例即可;
()学校总人数乘以组人数所占的比即可得出答案.
(1)解:本次调查学生总数:(名),
故答案为:;
(2)解:组:(名),组:(名),
补全统计图如图所示,
(3)解:组对应扇形的圆心角度数为,
故答案为:;
(4)解:估计该校研学活动时长为的学生人数为:(名),
答:估计该校研学活动时长为的学生人数有名.
9.(1)
(2)人
(3)有效,理由见解析
本题考查的从条形图与扇形图中获取信息,理解题意是关键;
(1)由乘以“答对4道”的占比即可得到答案;
(2)由乘以第一次测试答对4道及以上的占比即可得到答案;
(3)由答对3道及以上的百分率的提升可得训练有效.
(1)解:在扇形统计图中,“答对4道”所在扇形的圆心角为:
;
(2)解:该校有1200名学生,第一次模拟测试达到“优秀”的学生人数有:
(人);
(3)解:学生的两周训练有效,理由如下:
∵第一次训练答对3道及以上占,
第二次训练答对3道及以上占.
10.(1)200;图见解析
(2)
(3)460人
本题主要考查了条形统计图和扇形统计图,样本估计总体:
(1)用最喜欢“D羽毛球”的学生人数除以其所占的百分比,可得样本容量,求出最喜欢“B足球”的学生人数,即可求解;
(2)再用360度乘以最喜欢“C排球”的学生人数所占的百分比,即可求解;
(3)用2000乘以最喜欢“E乒乓球”的学生人数所占的百分比,即可求解.
(1)解:本次调查的样本容量是;
最喜欢“B足球”的学生人数为人,
补全条形统计图,如图:
;
(2)解:扇形统计图中C对应圆心角的度数为;
(3)解:人,
即该校最喜欢“E乒乓球”的学生人数为460人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
由样本所占百分比估计总体的数量综合题典型题型
归纳练 2025年中考数学二轮复习备考
一、解答题
1.为丰富学生业余活动,某中学决定再增加四种选修课,分别是:.青春舌战辩论;.时政瞭望;.美食与地理;.动漫创作,为了解学生喜好,在全校七年级范围内展开抽样问卷调查每位被调查的同学必须选择且只能选择一种,将数据进行整理后绘制成如下两幅不完整的统计图.
请根据上述信息,解答下列问题:
(1)这次一共调查了______名学生,并补全条形统计图;
(2)求扇形统计图中所对应的扇形的圆心角度数;
(3)若该地区七年级学生共有人,估计该地区七年级学生中喜欢“动漫创作”的学生有多少人?
2.某学校为了掌握中考复习状况,对会考指导讲解阶段学生课堂参与的深度和广度进行调查,其项目为:主动质疑、独立思考、专注听讲、能为他人讲解题目四项.调查组随机抽取了若干名九年级学生的课堂参与情况,获得了初步数据如下:
主动质疑:80人,独立思考120人,专注听讲160人,能为他人讲题学生若干,绘制了如下图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)这次评价中一共抽查了_____名学生;
(2)请将条形统计图补充完整;
(3)若全校有2000名九年级学生,请估计在复习后期模拟试卷讲评课中,“主动质疑”的学生约有多少人?
3.某校组织全体学生参加一次大型知识竞赛,从中随机抽取部分学生的竞赛成绩组成一个样本.所有学生的竞赛成绩分为四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.现根据抽取的学生的竞赛成绩绘制了如下两幅不完整的统计图.请你根据信息,解答下列问题:
抽取的学生的竞赛成绩条形统计图
抽取的学生的竞赛成绩扇形统计图
(1)在抽取的样本中,等级、等级的各有多少人?请把条形统计图补充完整.
(2)在扇形统计图中,求等级所对应的圆心角的度数.
(3)若知识竞赛成绩等级为优秀,请你估计该校参加竞赛的1500名学生中成绩优秀的人数.
4.学校为了响应国家“五育并举”的号召,增强学生体质,计划开展阳光体育锻炼活动.学校准备开设以下四个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),要求每位学生必须参加,且只能选择其中一项,并将选择项目的抽样调查结果绘制成如下不完整的统计图,请你结合图中信息解答下列问题:
(1)本次调查的学生人数是______人;
(2)在扇形统计图中,B对应的圆心角为______度;
(3)已知该学校共有2000名学生,请根据样本估计全校选择篮球的人数是多少?
5.经过两年多的建设和一年多的运营,市的“工业遗址文化乐园”已逐渐成为周边地区学生开展研学活动的基地之一.为进一步优化产品项目,提升服务水平,某天园区工作人员随机抽取了“向晖中学”部分到访的学生,开展对园区内四个品牌游乐项目(:工业之旅;:地质探险;:工程模拟;:极限挑战)受欢迎程度的调查,工作人员初步绘制了如下统计图表(不完整):
(1)参与本次调查的学生总人数_______,喜欢项目的学生人数_______;
(2)求参与本次调查的学生中喜欢项目的学生人数,并将条形统计图补充完整;
(3)若“向晖中学”共有名学生,试估计该校喜欢项目的学生人数.
6.某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:足球,篮球,羽毛球,乒乓球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有______人,在扇形统计图中 D部分对应的圆心角的度数为______;
(2)请你将条形统计图补充完整;
(3)学校共有1200名学生,根据统计信息,请你估算最喜欢篮球项目的学生人数.
7.某校在新学期之初举办了一场以“环保”为主题的综合实践知识竞赛,并把随机抽取的若干八年级学生的竞赛成绩进行整理,绘制成如下不完整的统计表和统计图.
组别 成绩(分) 频数
A 2
B a
C 14
D b
E 10
(1)写出a,b的值,并补全频数直方图.
(2)求扇形统计图中,A组所对应的圆心角度数.
(3)该校八年级共有480人,根据统计信息,估计该校八年级学生的竞赛成绩在D组的人数.
8.某学校开展了以“红色文化”为主题的研学活动,为了解学生参与情况,随机抽取部分学生对研学活动时长(用表示,单位:)进行调查.经过整理,将数据分成四组(组:;组:;组:;组:,并绘制了如下不完整的条形统计图和扇形统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了_____名学生;
(2)补全条形统计图;
(3)扇形统计图中,组对应的扇形圆心角的度数是_____;
(4)若该学校共有学生名,请估计该校研学活动时长为的学生人数.
9.某校为了解学生的数学素养,随机抽取100名学生进行模拟测试(每位学员答5道数学题,其中答对4道及以上为优秀),经过两周训练,对这些学生进行第二次模拟测试,将这两次模拟成绩进行整理、分析,并制作成如下统计表.
(1)在扇形统计图中,“答对4道”所在扇形的圆心角为________度.
(2)若该校有1200名学生,估计第一次模拟测试达到“优秀”的学生人数.
(3)你认为学生的两周训练是否有效?请用相关统计量说明理由.
10.某校为丰富学生的课余生活,开展了多姿多彩的体育活动,开设了五种球类运动项目:A篮球,B足球,C排球,D羽毛球,E乒乓球.为了解学生最喜欢以上哪种球类运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并绘制了统计图.某同学不小心将图中部分数据丢失,请结合统计图,完成下列问题:
(1)本次随机抽取多少名学生进行调查?并补全条形统计图;
(2)求扇形统计图中C对应圆心角的度数;
(3)若该校共有2000名学生,请你估计该校最喜欢“E乒乓球”的学生人数.
参考答案
1.(1),作图见解析
(2)
(3)人
本题考查条形统计图和扇形统计图的关联、求扇形统计图中扇形的圆心角的度数、用样本估计总体,理解题意,能从统计图中获取有用信息是解答的关键.
(1)用喜欢选修课A的学生人数除以其所占的百分比调查总人数,进而求得喜欢选修课C的学生人数,然后补全条形统计图即可;
(2)用乘以所占的百分比即可求解;
(3)用学生总人数乘以样本中喜欢“动漫创作”的学生所占比例即可求解.
(1)解:调查总数为名,
喜欢“美食与地理”的人数为(名),
补全条形统计图如图所示:
故答案为:800;
(2)解:,
答:所对应的扇形的圆心角度数为;
(3)解:人,
答:估计该地区七年级学生中喜欢“动漫创作”的学生有人.
2.(1)400
(2)见解析
(3)400人
本题考查了条形统计图与扇形统计图信息相关联,用样本估计总体数量等知识,从统计图中获取必要的信息是解题的关键.
(1)根据专注听讲的人数及其所占的百分数,可求得抽查的学生人数;
(2)抽查的总人数分别减去主动质疑、独立思考、专注听讲的人数,求得讲解题目的人数,从而可补充条形统计图;
(3)主动质疑学生人数所占的百分比与全校九年级学生人数的乘积,即为所求.
(1)解:由题意知,抽查的学生人数为:(名)
故答案为:400;
(2)解:讲解题目的人数为:(人),
补充条形统计图如下:
(3)解:(人)
答:在复习后期模拟试卷讲评课中,“主动质疑”的学生约有400人.
3.(1)等级有50人,等级有40人,图见解析
(2)
(3)375名
本题主要考查了条形统计图和扇形统计图的关联,用样本估计总体,求扇形统计图中的圆心角的度数,熟练掌握以上知识是解题的关键.
(1)根据B组人数除以B组所占的百分比即可求出抽取的学生总人数,进而求得等级、等级的人数即可;
(2)先求出D级人数所占的百分比,再利用乘以这个百分比,即可求出D级对应扇形的圆心角的度数.
(3)根据总人数乘以成绩优秀学生所占的百分比即可求出本次竞赛的学生中成绩为优秀的学生人数.
(1)解:共抽取总人数为(人),
则等级人数为(人),
等级人数为(人),
补全条形统计图如图所示:
(2)解:等级所对应的圆心角的度数为;
(3)解:(名),
答:估计该校参加竞赛的1500名学生中成绩优秀的人数为375名.
4.(1)100
(2)
(3)520
本题主要考查了条形统计图和扇形统计图的综合运用、用样本估计整体等知识点读懂统计图,从不同的统计图中得到必要的信息是解题的关键,
(1)直接利用排球的人数除以其所占百分比即可求得总人数;
(2)用总人数减去A、C、D的人数求出选择乒乓球的人数,然后利用乘B的人数所占的比例即可;
(4)用总人数乘以选择篮球的人数所占的比例即可解答.
(1)解:本次调查的学生人数是(人).
故答案为:100.
(2)解:本次调查的学生中选择B(乒乓球)的人数为(人),
在扇形统计图中,B对应的圆心角为.
故答案为:.
(3)解:(人),
答:估计全校选择篮球的人数是520人.
5.(1),
(2)补图见解析
(3)名
()用项目学生人数除以其百分比可求出本次调查的学生总人数,进而可求出喜欢项目的学生人数;
()求出参与本次调查的学生中喜欢项目的学生人数,进而补全条形统计图即可;
()用乘以喜欢项目的学生人数占比即可求解;
本题考查了扇形统计图和条形统计图,样本估计总体,看懂统计图是解题的关键.
(1)解:参与本次调查的学生总人数为,
喜欢项目的学生人数为,
故答案为:,;
(2)解:参与本次调查的学生中喜欢项目的学生人数为,
∴将条形统计图补充完整如下:
(3)解:,
答:估计该校喜欢项目的学生人数为名.
6.(1)200,
(2)见解析
(3)480人
本题考查的是条形统计图和扇形统计图的综合运用,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)利用扇形统计图得到A类的百分比为,则用A类的频数除以可得到样本容量;然后用D类的百分比乘以得到在扇形统计图中“D”对应的圆心角的度数;
(2)先计算出C类的频数,然后补全统计图;
(3)利用总人数乘以对应的比例即可求解.
(1)解:(人),
所以这次被调查的学生共有200人,
在扇形统计图中“D”对应的圆心角的度数;
故答案为:200,;
(2)解:类人数为(人),
完整条形统计图为:
(3)解:(人),
答:估算最喜欢篮球项目的学生人数为480人.
7.(1),见解析;
(2)
(3)192人
本题考查频数分布表、扇形统计图、条形统计图、样本估计总体,解题的关键是从频数分布表和扇形统计图中获取关键信息.
(1)根据E组频数及所占百分数求出班级的总人数,进而可求出a、b;根据求出的a、b补全即可;
(2)先求出本次调查中A组的占比,再与360°相乘,即可作答;
(3)本次调查中八年级中分数在D组的占比与480相乘,即可作答.
(1)解:班级总人数为:,
∴
,
补全条形统计图如下:
(2)解:,
∴A组对应的圆心角的度数为;
(3)解:(人),
∴估计八年级中分数在D组的人数为192人.
8.(1);
(2)补全统计图见解析;
(3);
(4)估计该校研学活动时长为的学生人数有名.
本题考查了条形统计图,扇形统计图,圆心角,用样本估计总体,解题的关键在于对知识的熟练掌握与灵活运用.
()用“”组的人数除以所占比例即可得出答案;
()先求出“”组的人数,然后利用总人数减去,,组人数,即可补全条形统计图;
()用乘以“”所占的比例即可;
()学校总人数乘以组人数所占的比即可得出答案.
(1)解:本次调查学生总数:(名),
故答案为:;
(2)解:组:(名),组:(名),
补全统计图如图所示,
(3)解:组对应扇形的圆心角度数为,
故答案为:;
(4)解:估计该校研学活动时长为的学生人数为:(名),
答:估计该校研学活动时长为的学生人数有名.
9.(1)
(2)人
(3)有效,理由见解析
本题考查的从条形图与扇形图中获取信息,理解题意是关键;
(1)由乘以“答对4道”的占比即可得到答案;
(2)由乘以第一次测试答对4道及以上的占比即可得到答案;
(3)由答对3道及以上的百分率的提升可得训练有效.
(1)解:在扇形统计图中,“答对4道”所在扇形的圆心角为:
;
(2)解:该校有1200名学生,第一次模拟测试达到“优秀”的学生人数有:
(人);
(3)解:学生的两周训练有效,理由如下:
∵第一次训练答对3道及以上占,
第二次训练答对3道及以上占.
10.(1)200;图见解析
(2)
(3)460人
本题主要考查了条形统计图和扇形统计图,样本估计总体:
(1)用最喜欢“D羽毛球”的学生人数除以其所占的百分比,可得样本容量,求出最喜欢“B足球”的学生人数,即可求解;
(2)再用360度乘以最喜欢“C排球”的学生人数所占的百分比,即可求解;
(3)用2000乘以最喜欢“E乒乓球”的学生人数所占的百分比,即可求解.
(1)解:本次调查的样本容量是;
最喜欢“B足球”的学生人数为人,
补全条形统计图,如图:
;
(2)解:扇形统计图中C对应圆心角的度数为;
(3)解:人,
即该校最喜欢“E乒乓球”的学生人数为460人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
