鲁教版(五四制)八年级下册数学 9.8 相似三角形的性质(2) 课件 (共20张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学 9.8 相似三角形的性质(2) 课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 852.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 08:29:59 | ||
图片预览






文档简介
(共20张PPT)
9.8 相似三角形的性质(2)
鲁教版五四学制八年级数学下册课件
01 复习巩固
02 新课导入
03 课堂检测
04 延伸拓展
目录
复习巩固
第壹部分
相似三角形的性质
相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比.
新课导入
新课导入
第貳部分
1.△ABC与△A′B′C′的相似比为1:5,如果A′C′边上的中线B′D′=20cm,则AC边上的中线BD=____ .
2.如图△ABC∽△A′B′C′,对应中线AD=6 cm,A′D′=10 cm,若BC=4.2 cm,则B′C′=______.
4cm
7cm
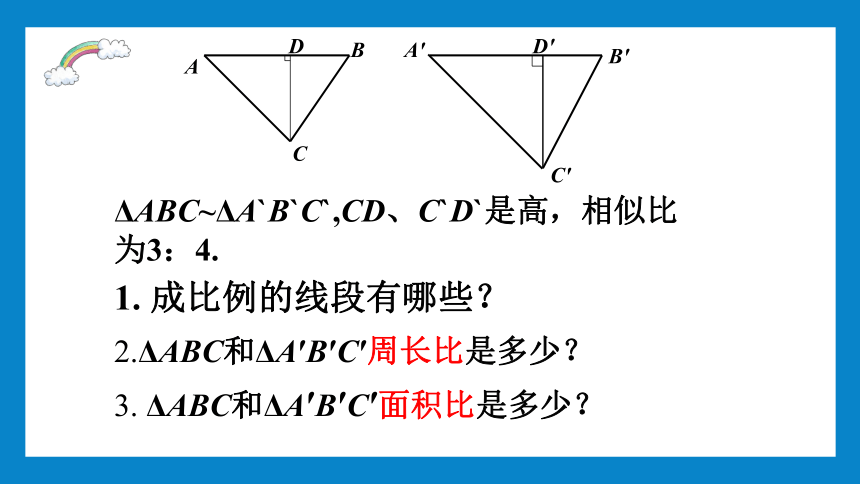
ΔABC~ΔA`B`C`,CD、C`D`是高,相似比为3:4.
A
B
C
D
A'
B'
C'
D'
1. 成比例的线段有哪些?
2.ΔABC和ΔA′B′C′周长比是多少?
3. ΔABC和ΔA′B′C′面积比是多少?
A
B
C
D
A'
B'
C'
D'
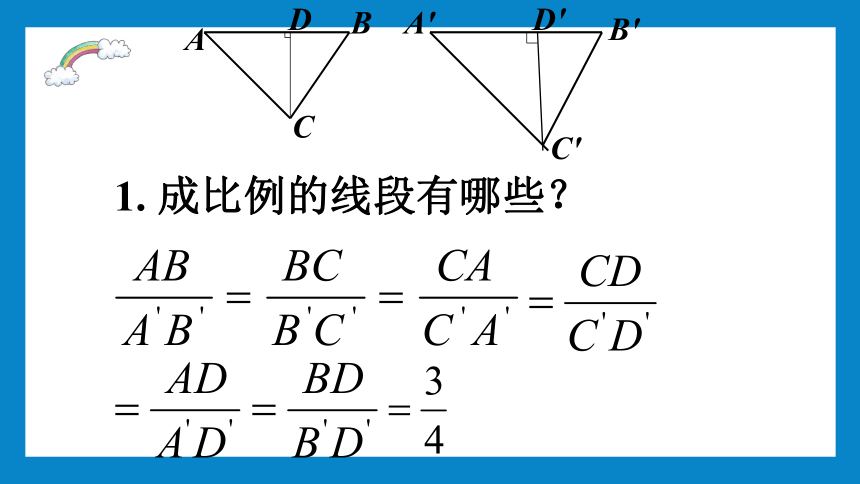
1. 成比例的线段有哪些?
A
B
C
D
A'
B'
C'
D'
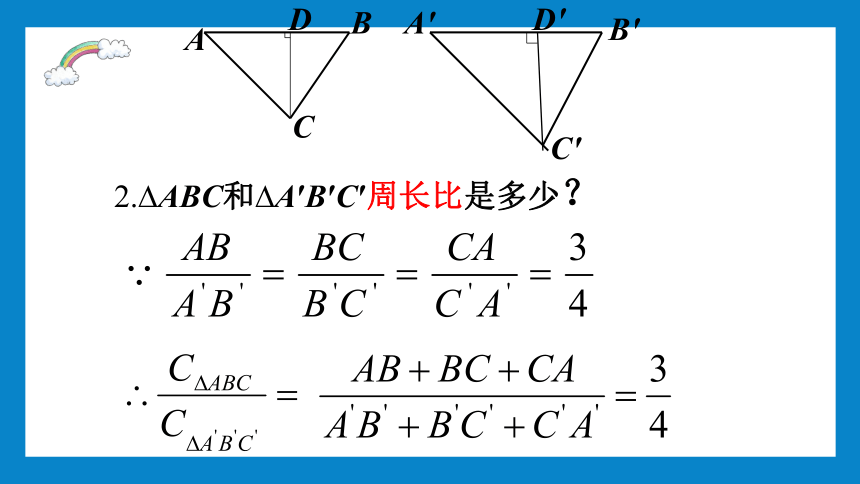
2. ABC和 A′B′C′周长比是多少?
A
B
C
D
A'
B'
C'
D'
3. ABC和 A′B′C′面积比是多少?
A
B
C
D
A'
B'
C'
D'
3. △ABC和△A′B′C′面积比是多少?
___
=
______
课堂检测
第叁部分
上题中,△ABC~△A′B′C′, 如果相似比为k,那么周长比应该是多少?
面积比呢?
课堂检测
相似三角形的周长比等于______,面积比等于_____________
相似比
相似比的平方.
课堂检测
四边形ABCD~四边形EFGH,相似比为K.
A
B
C
D
E
F
G
H
讨论:它们的周长比会是多少?
它们的面积比会是多少?
例2 如图,将△ABC沿BC方向平移得到△DEF, ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB,
∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC(两角分别相等的两个三角形相似).
∴ (相似三角形
面积的比等于相似比的平方),
即
∴EC2=2.∴EC= .
∴BE=BC-EC=2- ,
即△ABC平移的距离
为2-
延伸拓展
第肆部分
判断题:
1.如果把一个三角形三边长同时扩大为原来的10倍,那么它的周长也扩大为原来的10倍.
(Y)
2. 如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍.
(N)
相似多边形的性质:
相似三角形对应高的比,对应角平分线的比,对应中线的比,对应周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
相似多边形对应对角线的比等于相似比.
相似多边形对应三角形相似,且相似比等于相似多边形的相似比.
相似多边形对应三角形面积的比等于相似多边形的相似比的平方.
相似多边形面积的比等于相似比的平方.
延伸拓展
9.8 相似三角形的性质(2)
鲁教版五四学制八年级数学下册课件
9.8 相似三角形的性质(2)
鲁教版五四学制八年级数学下册课件
01 复习巩固
02 新课导入
03 课堂检测
04 延伸拓展
目录
复习巩固
第壹部分
相似三角形的性质
相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比.
新课导入
新课导入
第貳部分
1.△ABC与△A′B′C′的相似比为1:5,如果A′C′边上的中线B′D′=20cm,则AC边上的中线BD=____ .
2.如图△ABC∽△A′B′C′,对应中线AD=6 cm,A′D′=10 cm,若BC=4.2 cm,则B′C′=______.
4cm
7cm
ΔABC~ΔA`B`C`,CD、C`D`是高,相似比为3:4.
A
B
C
D
A'
B'
C'
D'
1. 成比例的线段有哪些?
2.ΔABC和ΔA′B′C′周长比是多少?
3. ΔABC和ΔA′B′C′面积比是多少?
A
B
C
D
A'
B'
C'
D'
1. 成比例的线段有哪些?
A
B
C
D
A'
B'
C'
D'
2. ABC和 A′B′C′周长比是多少?
A
B
C
D
A'
B'
C'
D'
3. ABC和 A′B′C′面积比是多少?
A
B
C
D
A'
B'
C'
D'
3. △ABC和△A′B′C′面积比是多少?
___
=
______
课堂检测
第叁部分
上题中,△ABC~△A′B′C′, 如果相似比为k,那么周长比应该是多少?
面积比呢?
课堂检测
相似三角形的周长比等于______,面积比等于_____________
相似比
相似比的平方.
课堂检测
四边形ABCD~四边形EFGH,相似比为K.
A
B
C
D
E
F
G
H
讨论:它们的周长比会是多少?
它们的面积比会是多少?
例2 如图,将△ABC沿BC方向平移得到△DEF, ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB,
∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC(两角分别相等的两个三角形相似).
∴ (相似三角形
面积的比等于相似比的平方),
即
∴EC2=2.∴EC= .
∴BE=BC-EC=2- ,
即△ABC平移的距离
为2-
延伸拓展
第肆部分
判断题:
1.如果把一个三角形三边长同时扩大为原来的10倍,那么它的周长也扩大为原来的10倍.
(Y)
2. 如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍.
(N)
相似多边形的性质:
相似三角形对应高的比,对应角平分线的比,对应中线的比,对应周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
相似多边形对应对角线的比等于相似比.
相似多边形对应三角形相似,且相似比等于相似多边形的相似比.
相似多边形对应三角形面积的比等于相似多边形的相似比的平方.
相似多边形面积的比等于相似比的平方.
延伸拓展
9.8 相似三角形的性质(2)
鲁教版五四学制八年级数学下册课件
