华师大版七下(2024版)9.1.1生活中的轴对称教案
文档属性
| 名称 | 华师大版七下(2024版)9.1.1生活中的轴对称教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 08:34:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《9.1.1生活中的轴对称》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本节课主要以现实生中的对称引入,通过观察、分析现实生活实例和典型图形的过程,认识轴对称和轴对称图形,会找出简单的轴对称图形的对称轴,了解轴对称和轴对称图形的联系和区别,通过欣赏现实生活中的轴对称图形,让学生体验轴对称在现实生活中的广泛应用,体会数学来源于生活。
学习者分析 学生在学习本节课之前曾经学过轴对称图形:等腰三角形、长方形、正方形、圆等图形,也学过线段的基本性质,角平分线定义,所以本节课是通过具体实例认识轴对称,欣赏生活中的轴对称图形,体验轴对称在现实生活中的运用,在探索中发现轴对称图形的性质。
教学目标 1.通过观察、分析现实生活中的实例和典型图形,认识轴对称和轴对称图形. 2.会找出简单的轴对称图形的对称轴. 3.理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称图形的基本特征. 4.通过欣赏现实生活中的轴对称图形,体验轴对称在现实生活中的广泛应用,体会数学来源于生活.
教学重点 轴对称图形的概念及判断图形是否是轴对称图形.
教学难点 寻找轴对称图形的对称轴,轴对称图形与成轴对称的区别与联系.
学习活动设计
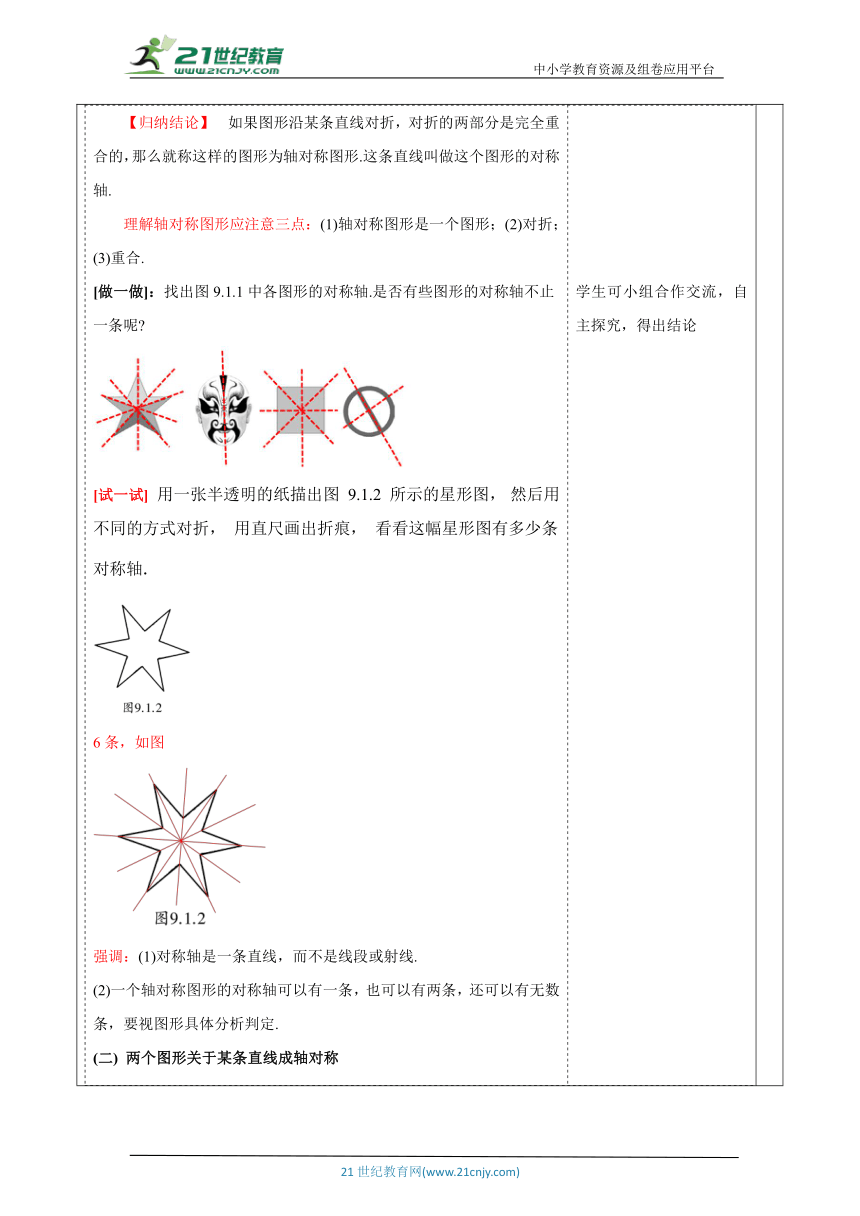
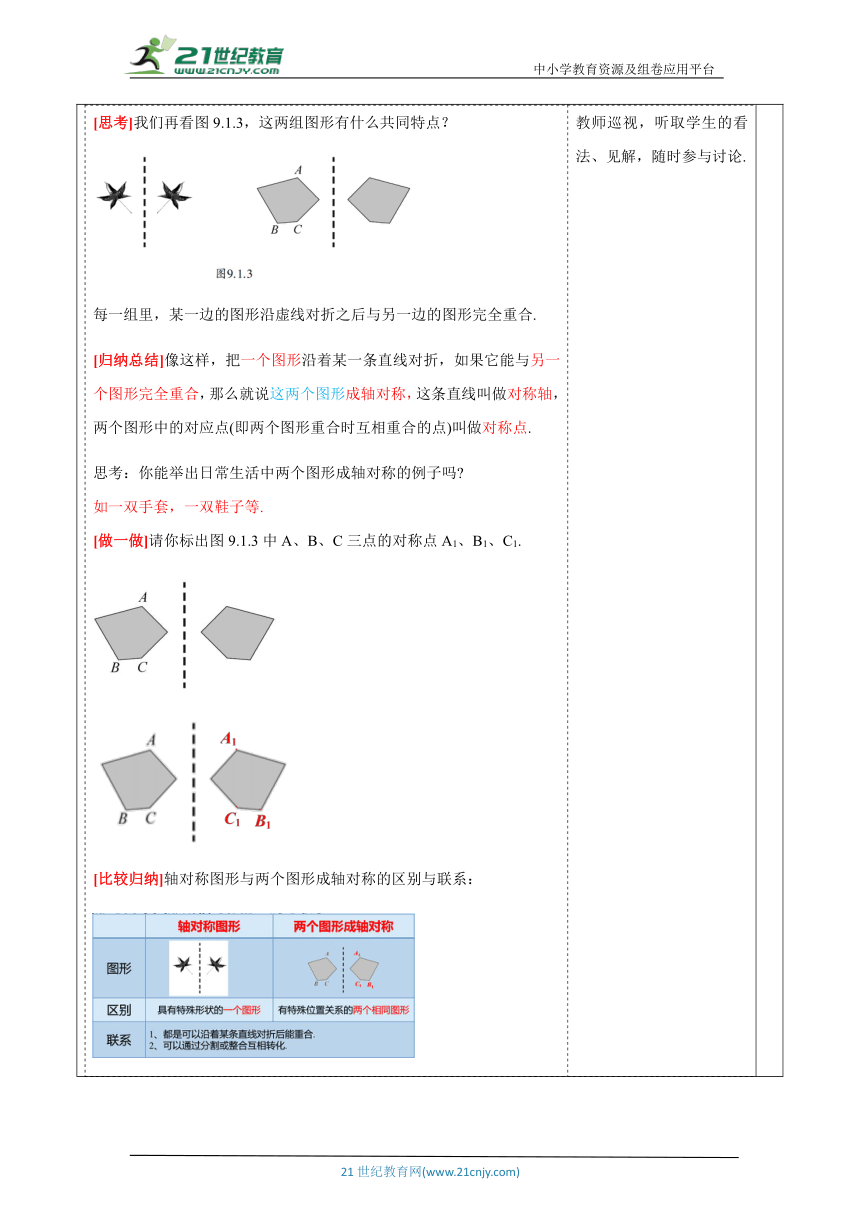
教师活动学生活动环节一:情境导入教师活动1: 世界充满着运动,从天体、星球的运行,到原子、粒子的作用,其中最基本的是轴对称、平移、旋转等运动.轴对称、平移与旋转等合成了大千世界千姿百态的运动. 本章将探究在轴对称、平移与旋转的图形变化下图形的不变性质,并应用轴对称、平移与旋转等方法进行图案设计,从中体会图形变化在几何研究中的作用.学生活动1: 通过探究活动理解.学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知. 激发学生探究生活中的轴对称,从生活中观察轴对称的现象.活动意图说明: 从实际出发,从学生已有的生活经验出发.初步体会现实生活中的图形,引出本节内容轴对称.环节二:新知探究教师活动2: (一)轴对称图形 不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的. 这些图形,你可能都见过.把它们沿着某条直线对折一下,看看对折后的两部分能完全重合吗?如果折一次得不到你想要的结果,那再多折几次试试. 【归纳结论】 如果图形沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形.这条直线叫做这个图形的对称轴. 理解轴对称图形应注意三点:(1)轴对称图形是一个图形;(2)对折;(3)重合. [做一做]:找出图9.1.1中各图形的对称轴.是否有些图形的对称轴不止一条呢 [试一试] 用一张半透明的纸描出图 9.1.2 所示的星形图, 然后用不同的方式对折, 用直尺画出折痕, 看看这幅星形图有多少条对称轴. 如图 强调:(1)对称轴是一条直线,而不是线段或射线. (2)一个轴对称图形的对称轴可以有一条,也可以有两条,还可以有无数条,要视图形具体分析判定. (二) 两个图形关于某条直线成轴对称 [思考]我们再看图9.1.3,这两组图形有什么共同特点? 每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合. [归纳总结]像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点. 思考:你能举出日常生活中两个图形成轴对称的例子吗 如一双手套,一双鞋子等. [做一做]请你标出图9.1.3中A、B、C三点的对称点A1、B1、C1. [比较归纳]轴对称图形与两个图形成轴对称的区别与联系: (三)轴对称(或成轴对称图形)的基本特征 思考:如图9.1.3中,两个图形有什么基本特征? [归纳总结]轴对称图形的基本特征: 轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的.所以轴对称图形(或成轴对称的两个图形)的对称线段(对折后重合的线段)相等,对应角(对折后能够重合的角)相等.学生活动2: 学生小组合作交流. 学生可小组合作交流,自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论. 活动意图说明:引导学生建立模型,鼓励学生大胆探索,会找出简单的轴对称图形的对称轴,了解轴对称和轴对称图形的联系和区别.理解轴对称(或成轴对称图形)的基本特征,积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1下列交通标志图案是轴对称图形的是( ) A. B. C. D. 【分析】根据轴对称图形的概念可知,只有B是轴对称图形. 【答案】B 【总结】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就是轴对称图形. 例2 观察图中的图形,哪些图形是轴对称图形?如果是轴对称图形,请找出它的对称轴. 【分析】轴对称图形的对称轴都有几条呢? 【解】第一、二、三、五、六个图形是轴对称图形,它们的对称轴如图. 【总结】判断一个图形是否为轴对称图形,关键是看能否找到一条直线,沿这条直线折叠,使它两旁的部分能够互相重合. 例3 如图所示,哪一组的右边图形与左边图形成轴对称? 【分析】轴对称和轴对称图形的区别是什么?怎样区别它们呢? 【解】④⑤⑥中右边图形与左边图形成轴对称. 【总结】把一个图形沿某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称. 例4 如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角. 【分析】在本题中我们能说线段AF为对称轴吗? 学生思考,学生代表发言:不可以,∵对称轴是直线,而AF是线段. 【解】相等的线段:AB=AE,CB=DE,CF=DF;相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFC=∠AFD. 【总结】在轴对称图形或成轴对称的两个图形中,注意:对称轴是一条直线.学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 活动意图说明: 让学生在一定的数学活动中去体验、感受数学,通过对例题的学习,进一步加深对三角形的概念和三角形分类的理解和掌握.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 9.1.1生活中的轴对称 轴对称图形: 对称轴: 区别: 轴对称的基本特征: 例1: 例2: 例3: 例4:
课堂练习 【知识技能类作业】 必做题: 1.下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案不是轴对称图形的是( ) A.B.C. D. 2.如图,在下列四个图形中,是轴对称图形的是( ) A.B.C. D. 3.下列图形中对称轴最多的是 选做题: 4.如图所示,其中与甲成轴对称的图形是 . 5.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 点. 6.正方形的对称轴的条数为 . 【综合拓展类作业】 7.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图)。请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形。 8.已知在同一平面内的两条相等线段,它们通过一次或两次轴对称变化就可以重合.如图,方格纸上的每个小方格都是边长为1个单位长度的正方形,点,,,都在格点上,请分别在图1、图2中画出对称轴,使得线段通过轴对称变化能与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段. 1.【答案】B 2.【答案】C 3.【答案】圆 4.【答案】丁 5.【答案】D 6.【答案】4 7.【答案】解:答案不唯一,如图所示, 8.【答案】解:如图1、图2所示.
作业设计 【知识技能类作业】 必做题: 1.数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( ) A B C D 2.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠D=80°,则∠BAD的度数为( ) 第2题图 A.170° B.150° C.130° D.110° 3.如图,△ABC与△A'B'C'关于直线l对称,且∠A=105°,∠C'=30°,则∠B的度数为( ) 第3题图 A.25° B.45° C.30° D.20° 选做题: 4.将一张正方形纸片按如图步骤①②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( ) A B C D 5.如图,在△ABC中,点D、E分别在边AB、BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为( ) 第5题图 A.9 B.10 C.11 D.12 6.围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,则所得的对弈图是轴对称图形.(填写A、B、C、D中的一处即可,A、B、C、D位于棋盘的格点上) 第6题图 【综合拓展类作业】 7.如图,在△ABC中,将∠B、∠C按如图所示的方式折叠,点B、C均落于边BC上的点Q处,MN、EF为折痕.若∠A=82°,则∠MQE的度数为 . 8.如图,弹性小球从点P出发,沿图所示的方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到长方形的边时,反弹点为Q,第2次碰到长方形的边时,反弹点为M……则第2025次碰到长方形的边时,反弹点为图中的( ) A.点P B.点Q C.点M D.点N 1.B 2.C 3.B 4.A 5.B 6.A或C 7.82° 8.D
教学反思 本节课充分利用多媒体教学,给学生以直观指导,主动向学生质疑,促使学生思考与发现,形成认识,使学生独立获取知识和技能.另外,借助多媒体教学给学生创设宽松的学习氛围,使学生在学习中始终保持兴奋、愉悦、渴求思索的心理状态,有利于学生主体性的发挥和创新能力的培养.
21世纪教育网(www.21cnjy.com)
分课时教学设计
《9.1.1生活中的轴对称》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本节课主要以现实生中的对称引入,通过观察、分析现实生活实例和典型图形的过程,认识轴对称和轴对称图形,会找出简单的轴对称图形的对称轴,了解轴对称和轴对称图形的联系和区别,通过欣赏现实生活中的轴对称图形,让学生体验轴对称在现实生活中的广泛应用,体会数学来源于生活。
学习者分析 学生在学习本节课之前曾经学过轴对称图形:等腰三角形、长方形、正方形、圆等图形,也学过线段的基本性质,角平分线定义,所以本节课是通过具体实例认识轴对称,欣赏生活中的轴对称图形,体验轴对称在现实生活中的运用,在探索中发现轴对称图形的性质。
教学目标 1.通过观察、分析现实生活中的实例和典型图形,认识轴对称和轴对称图形. 2.会找出简单的轴对称图形的对称轴. 3.理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称图形的基本特征. 4.通过欣赏现实生活中的轴对称图形,体验轴对称在现实生活中的广泛应用,体会数学来源于生活.
教学重点 轴对称图形的概念及判断图形是否是轴对称图形.
教学难点 寻找轴对称图形的对称轴,轴对称图形与成轴对称的区别与联系.
学习活动设计
教师活动学生活动环节一:情境导入教师活动1: 世界充满着运动,从天体、星球的运行,到原子、粒子的作用,其中最基本的是轴对称、平移、旋转等运动.轴对称、平移与旋转等合成了大千世界千姿百态的运动. 本章将探究在轴对称、平移与旋转的图形变化下图形的不变性质,并应用轴对称、平移与旋转等方法进行图案设计,从中体会图形变化在几何研究中的作用.学生活动1: 通过探究活动理解.学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知. 激发学生探究生活中的轴对称,从生活中观察轴对称的现象.活动意图说明: 从实际出发,从学生已有的生活经验出发.初步体会现实生活中的图形,引出本节内容轴对称.环节二:新知探究教师活动2: (一)轴对称图形 不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的. 这些图形,你可能都见过.把它们沿着某条直线对折一下,看看对折后的两部分能完全重合吗?如果折一次得不到你想要的结果,那再多折几次试试. 【归纳结论】 如果图形沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形.这条直线叫做这个图形的对称轴. 理解轴对称图形应注意三点:(1)轴对称图形是一个图形;(2)对折;(3)重合. [做一做]:找出图9.1.1中各图形的对称轴.是否有些图形的对称轴不止一条呢 [试一试] 用一张半透明的纸描出图 9.1.2 所示的星形图, 然后用不同的方式对折, 用直尺画出折痕, 看看这幅星形图有多少条对称轴. 如图 强调:(1)对称轴是一条直线,而不是线段或射线. (2)一个轴对称图形的对称轴可以有一条,也可以有两条,还可以有无数条,要视图形具体分析判定. (二) 两个图形关于某条直线成轴对称 [思考]我们再看图9.1.3,这两组图形有什么共同特点? 每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合. [归纳总结]像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点. 思考:你能举出日常生活中两个图形成轴对称的例子吗 如一双手套,一双鞋子等. [做一做]请你标出图9.1.3中A、B、C三点的对称点A1、B1、C1. [比较归纳]轴对称图形与两个图形成轴对称的区别与联系: (三)轴对称(或成轴对称图形)的基本特征 思考:如图9.1.3中,两个图形有什么基本特征? [归纳总结]轴对称图形的基本特征: 轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的.所以轴对称图形(或成轴对称的两个图形)的对称线段(对折后重合的线段)相等,对应角(对折后能够重合的角)相等.学生活动2: 学生小组合作交流. 学生可小组合作交流,自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论. 活动意图说明:引导学生建立模型,鼓励学生大胆探索,会找出简单的轴对称图形的对称轴,了解轴对称和轴对称图形的联系和区别.理解轴对称(或成轴对称图形)的基本特征,积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1下列交通标志图案是轴对称图形的是( ) A. B. C. D. 【分析】根据轴对称图形的概念可知,只有B是轴对称图形. 【答案】B 【总结】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就是轴对称图形. 例2 观察图中的图形,哪些图形是轴对称图形?如果是轴对称图形,请找出它的对称轴. 【分析】轴对称图形的对称轴都有几条呢? 【解】第一、二、三、五、六个图形是轴对称图形,它们的对称轴如图. 【总结】判断一个图形是否为轴对称图形,关键是看能否找到一条直线,沿这条直线折叠,使它两旁的部分能够互相重合. 例3 如图所示,哪一组的右边图形与左边图形成轴对称? 【分析】轴对称和轴对称图形的区别是什么?怎样区别它们呢? 【解】④⑤⑥中右边图形与左边图形成轴对称. 【总结】把一个图形沿某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称. 例4 如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角. 【分析】在本题中我们能说线段AF为对称轴吗? 学生思考,学生代表发言:不可以,∵对称轴是直线,而AF是线段. 【解】相等的线段:AB=AE,CB=DE,CF=DF;相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFC=∠AFD. 【总结】在轴对称图形或成轴对称的两个图形中,注意:对称轴是一条直线.学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 活动意图说明: 让学生在一定的数学活动中去体验、感受数学,通过对例题的学习,进一步加深对三角形的概念和三角形分类的理解和掌握.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 9.1.1生活中的轴对称 轴对称图形: 对称轴: 区别: 轴对称的基本特征: 例1: 例2: 例3: 例4:
课堂练习 【知识技能类作业】 必做题: 1.下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案不是轴对称图形的是( ) A.B.C. D. 2.如图,在下列四个图形中,是轴对称图形的是( ) A.B.C. D. 3.下列图形中对称轴最多的是 选做题: 4.如图所示,其中与甲成轴对称的图形是 . 5.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 点. 6.正方形的对称轴的条数为 . 【综合拓展类作业】 7.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图)。请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形。 8.已知在同一平面内的两条相等线段,它们通过一次或两次轴对称变化就可以重合.如图,方格纸上的每个小方格都是边长为1个单位长度的正方形,点,,,都在格点上,请分别在图1、图2中画出对称轴,使得线段通过轴对称变化能与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段. 1.【答案】B 2.【答案】C 3.【答案】圆 4.【答案】丁 5.【答案】D 6.【答案】4 7.【答案】解:答案不唯一,如图所示, 8.【答案】解:如图1、图2所示.
作业设计 【知识技能类作业】 必做题: 1.数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( ) A B C D 2.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠D=80°,则∠BAD的度数为( ) 第2题图 A.170° B.150° C.130° D.110° 3.如图,△ABC与△A'B'C'关于直线l对称,且∠A=105°,∠C'=30°,则∠B的度数为( ) 第3题图 A.25° B.45° C.30° D.20° 选做题: 4.将一张正方形纸片按如图步骤①②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( ) A B C D 5.如图,在△ABC中,点D、E分别在边AB、BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为( ) 第5题图 A.9 B.10 C.11 D.12 6.围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,则所得的对弈图是轴对称图形.(填写A、B、C、D中的一处即可,A、B、C、D位于棋盘的格点上) 第6题图 【综合拓展类作业】 7.如图,在△ABC中,将∠B、∠C按如图所示的方式折叠,点B、C均落于边BC上的点Q处,MN、EF为折痕.若∠A=82°,则∠MQE的度数为 . 8.如图,弹性小球从点P出发,沿图所示的方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到长方形的边时,反弹点为Q,第2次碰到长方形的边时,反弹点为M……则第2025次碰到长方形的边时,反弹点为图中的( ) A.点P B.点Q C.点M D.点N 1.B 2.C 3.B 4.A 5.B 6.A或C 7.82° 8.D
教学反思 本节课充分利用多媒体教学,给学生以直观指导,主动向学生质疑,促使学生思考与发现,形成认识,使学生独立获取知识和技能.另外,借助多媒体教学给学生创设宽松的学习氛围,使学生在学习中始终保持兴奋、愉悦、渴求思索的心理状态,有利于学生主体性的发挥和创新能力的培养.
21世纪教育网(www.21cnjy.com)
