华师大版七下(2024版)9.1.1生活中的轴对称课件
文档属性
| 名称 | 华师大版七下(2024版)9.1.1生活中的轴对称课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 08:34:14 | ||
图片预览









文档简介
(共37张PPT)
第九章 轴对称、平移与旋转
9.1.1生活中的轴对称
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
通过观察、分析现实生活中的实例和典型图形,认识轴对称和轴对称图形.
01
会找出简单的轴对称图形的对称轴.
02
理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称图形的基本特征.
03
通过欣赏现实生活中的轴对称图形,体验轴对称在现实生活中的广泛应用,体会数学来源于生活.
04
02
新知导入
世界充满着运动,从天体、星球的运行,到原子、粒子的作用,其中最基本的是轴对称、平移、旋转等运动.轴对称、平移与旋转等合成了大千世界千姿百态的运动.
02
新知导入
本章将探究在轴对称、平移与旋转的图形变化下图形的不变性质,并应用轴对称、平移与旋转等方法进行图案设计,从中体会图形变化在几何研究中的作用.
03
新知探究
探究一
轴对称图形
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的.
03
新知探究
这些图形,你可能都见过.把它们沿着某条直线对折一下,看看对折后的两部分能完全重合吗?如果折一次得不到你想要的结果,那再多折几次试试.
探究一
轴对称图形
03
新知探究
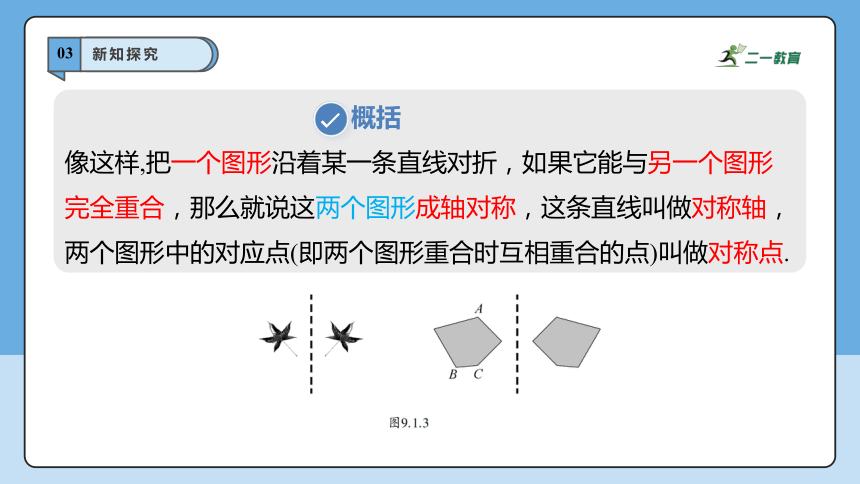
如果图形沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形.这条直线叫做这个图形的对称轴.
概括
(1)轴对称图形是一个图形;(2)对折;(3)重合.
注意
03
新知探究
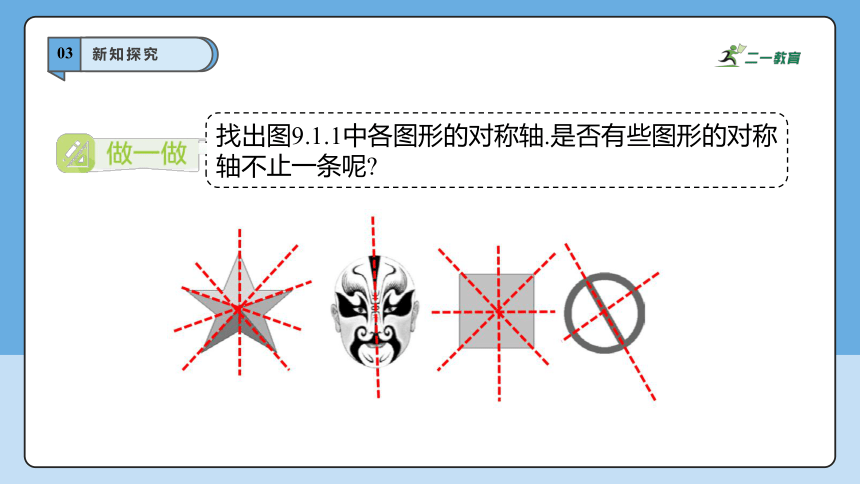
找出图9.1.1中各图形的对称轴.是否有些图形的对称轴不止一条呢
03
新知探究
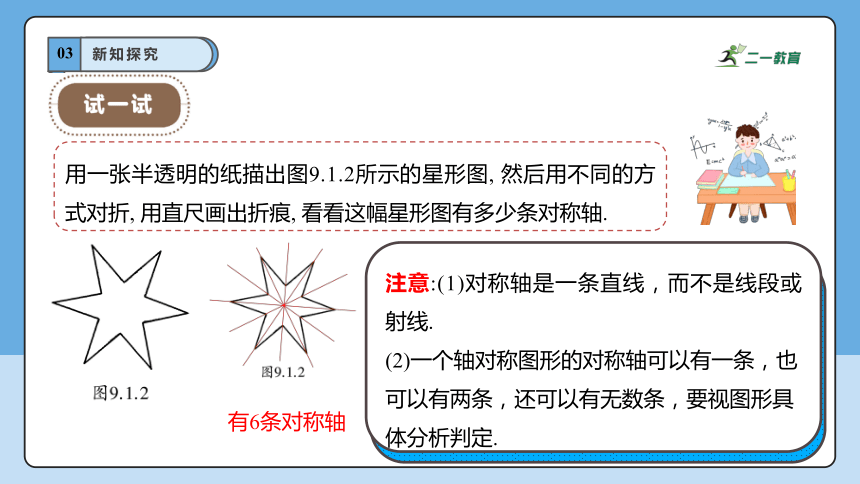
有6条对称轴
用一张半透明的纸描出图9.1.2所示的星形图, 然后用不同的方式对折, 用直尺画出折痕, 看看这幅星形图有多少条对称轴.
注意:(1)对称轴是一条直线,而不是线段或射线.
(2)一个轴对称图形的对称轴可以有一条,也可以有两条,还可以有无数条,要视图形具体分析判定.
03
新知探究
探究二
两个图形关于某条直线成轴对称
我们再看图9.1.3,这两组图形有什么共同特点?
每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
03
新知探究
像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
概括
03
新知探究
你能举出日常生活中两个图形成轴对称的例子吗
03
新知探究
请你标出图9.1.3中A、B、C三点的对称点A1、B1、C1.
03
新知探究
轴对称图形与两个图形成轴对称的区别与联系:
概括
轴对称图形 两个图形成轴对称
图形
区别 具有特殊形状的一个图形 有特殊位置关系的两个相同图形
联系 1、都是可以沿着某条直线对折后能重合. 2、可以通过分割或整合互相转化.
03
新知探究
探究三
轴对称(或成轴对称图形)的基本特征
思考:如图9.1.3中,两个图形有什么基本特征?
03
新知探究
轴对称图形的基本特征:
轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的.所以轴对称图形(或成轴对称的两个图形)的对称线段(对折后重合的线段)相等,对应角(对折后能够重合的角)相等.
概括
04
例题讲解
下列交通标志图案是轴对称图形的是( )
例1
总结
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就是轴对称图形.
B
04
例题讲解
观察图中的图形,哪些图形是轴对称图形?如果是轴对称图形,请找出它的对称轴.
例2
【解】第一、二、三、五、六个图形是轴对称图形,它们的对称轴如图.
04
例题讲解
总结
判断一个图形是否为轴对称图形,关键是看能否找到一条直线,沿这条直线折叠,使它两旁的部分能够互相重合.
04
例题讲解
如图所示,哪一组的右边图形与左边图形成轴对称?
例3
【解】④⑤⑥中右边图形与左边图形成轴对称.
总结
把一个图形沿某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
04
例题讲解
【解】相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFC=∠AFD.
总结
在轴对称图形或成轴对称的两个图形中, 对称轴是一条直线.
如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
例4
1.下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案不是轴对称图形的是( )
04
课堂练习
【知识技能类作业】必做题:
B
C
2.如图,在下列四个图形中,是轴对称图形的是( )
04
课堂练习
【知识技能类作业】必做题:
圆
3.下列图形中对称轴最多的是 .
4.如图所示,其中与甲成轴对称的图形是 .
04
课堂练习
【知识技能类作业】选做题:
丁
5.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 点.
D
6.正方形的对称轴的条数为 .
4
04
课堂练习
【知识技能类作业】选做题:
解:答案不唯一,如图所示:
7.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图)。请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形。
04
课堂练习
【知识技能类作业】选做题:
解:如图1、图2所示.
8.已知在同一平面内的两条相等线段,它们通过一次或两次轴对称变化就可以重合.如图,方格纸上的每个小方格都是边长为1个单位长度的正方形,点A,B,C,D都在格点上,请分别在图1、图2中画出对称轴,使得线段AB通过轴对称变化能与线段CD重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段.
05
课堂小结
生活中的轴对称
如果一个图形沿着某条直线对折,对折后的两部分完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
定义
轴对称图形的期末特征
轴对称图形:具有特殊形状的一个图形.
成轴对称:有特殊位置关系的两个相同图形.
区别
对应线段相等,对应角相等.
把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做对称点.
06
作业布置
【知识技能类作业】必做题:
1.数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
B
2.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠D=80°,则∠BAD的度数为( )
A.170° B.150° C.130° D.110°
C
3.如图,△ABC与△A'B'C'关于直线l对称,且∠A=105°,∠C'=30°,则∠B的度数为( )
A.25° B.45° C.30° D.20°
06
作业布置
【知识技能类作业】必做题:
B
06
作业布置
【知识技能类作业】选做题:
4.将一张正方形纸片按如图步骤①②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A
5.如图,在△ABC中,点D、E分别在边AB、BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为( )
A.9 B.10 C.11 D.12
06
作业布置
【知识技能类作业】选做题:
C
6.围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,则所得的对弈图是轴对称图形.(填写A、B、C、D中的一处即可,A、B、C、D位于棋盘的格点上)
06
作业布置
【知识技能类作业】选做题:
A或C
06
作业布置
【综合拓展类作业】
7.如图,在△ABC中,将∠B、∠C按如图所示的方式折叠,点B、C均落于边BC上的点Q处,MN、EF为折痕.若∠A=82°,则∠MQE的度数为 .
82°
06
作业布置
【综合拓展类作业】
D
8.如图,弹性小球从点P出发,沿图所示的方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到长方形的边时,反弹点为Q,第2次碰到长方形的边时,反弹点为M……则第2025次碰到长方形的边时,反弹点为图中的( )
A.点P B.点Q C.点M D.点N
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第九章 轴对称、平移与旋转
9.1.1生活中的轴对称
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
通过观察、分析现实生活中的实例和典型图形,认识轴对称和轴对称图形.
01
会找出简单的轴对称图形的对称轴.
02
理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称图形的基本特征.
03
通过欣赏现实生活中的轴对称图形,体验轴对称在现实生活中的广泛应用,体会数学来源于生活.
04
02
新知导入
世界充满着运动,从天体、星球的运行,到原子、粒子的作用,其中最基本的是轴对称、平移、旋转等运动.轴对称、平移与旋转等合成了大千世界千姿百态的运动.
02
新知导入
本章将探究在轴对称、平移与旋转的图形变化下图形的不变性质,并应用轴对称、平移与旋转等方法进行图案设计,从中体会图形变化在几何研究中的作用.
03
新知探究
探究一
轴对称图形
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的.
03
新知探究
这些图形,你可能都见过.把它们沿着某条直线对折一下,看看对折后的两部分能完全重合吗?如果折一次得不到你想要的结果,那再多折几次试试.
探究一
轴对称图形
03
新知探究
如果图形沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形.这条直线叫做这个图形的对称轴.
概括
(1)轴对称图形是一个图形;(2)对折;(3)重合.
注意
03
新知探究
找出图9.1.1中各图形的对称轴.是否有些图形的对称轴不止一条呢
03
新知探究
有6条对称轴
用一张半透明的纸描出图9.1.2所示的星形图, 然后用不同的方式对折, 用直尺画出折痕, 看看这幅星形图有多少条对称轴.
注意:(1)对称轴是一条直线,而不是线段或射线.
(2)一个轴对称图形的对称轴可以有一条,也可以有两条,还可以有无数条,要视图形具体分析判定.
03
新知探究
探究二
两个图形关于某条直线成轴对称
我们再看图9.1.3,这两组图形有什么共同特点?
每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
03
新知探究
像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
概括
03
新知探究
你能举出日常生活中两个图形成轴对称的例子吗
03
新知探究
请你标出图9.1.3中A、B、C三点的对称点A1、B1、C1.
03
新知探究
轴对称图形与两个图形成轴对称的区别与联系:
概括
轴对称图形 两个图形成轴对称
图形
区别 具有特殊形状的一个图形 有特殊位置关系的两个相同图形
联系 1、都是可以沿着某条直线对折后能重合. 2、可以通过分割或整合互相转化.
03
新知探究
探究三
轴对称(或成轴对称图形)的基本特征
思考:如图9.1.3中,两个图形有什么基本特征?
03
新知探究
轴对称图形的基本特征:
轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的.所以轴对称图形(或成轴对称的两个图形)的对称线段(对折后重合的线段)相等,对应角(对折后能够重合的角)相等.
概括
04
例题讲解
下列交通标志图案是轴对称图形的是( )
例1
总结
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就是轴对称图形.
B
04
例题讲解
观察图中的图形,哪些图形是轴对称图形?如果是轴对称图形,请找出它的对称轴.
例2
【解】第一、二、三、五、六个图形是轴对称图形,它们的对称轴如图.
04
例题讲解
总结
判断一个图形是否为轴对称图形,关键是看能否找到一条直线,沿这条直线折叠,使它两旁的部分能够互相重合.
04
例题讲解
如图所示,哪一组的右边图形与左边图形成轴对称?
例3
【解】④⑤⑥中右边图形与左边图形成轴对称.
总结
把一个图形沿某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
04
例题讲解
【解】相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFC=∠AFD.
总结
在轴对称图形或成轴对称的两个图形中, 对称轴是一条直线.
如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
例4
1.下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案不是轴对称图形的是( )
04
课堂练习
【知识技能类作业】必做题:
B
C
2.如图,在下列四个图形中,是轴对称图形的是( )
04
课堂练习
【知识技能类作业】必做题:
圆
3.下列图形中对称轴最多的是 .
4.如图所示,其中与甲成轴对称的图形是 .
04
课堂练习
【知识技能类作业】选做题:
丁
5.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 点.
D
6.正方形的对称轴的条数为 .
4
04
课堂练习
【知识技能类作业】选做题:
解:答案不唯一,如图所示:
7.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图)。请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形。
04
课堂练习
【知识技能类作业】选做题:
解:如图1、图2所示.
8.已知在同一平面内的两条相等线段,它们通过一次或两次轴对称变化就可以重合.如图,方格纸上的每个小方格都是边长为1个单位长度的正方形,点A,B,C,D都在格点上,请分别在图1、图2中画出对称轴,使得线段AB通过轴对称变化能与线段CD重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段.
05
课堂小结
生活中的轴对称
如果一个图形沿着某条直线对折,对折后的两部分完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
定义
轴对称图形的期末特征
轴对称图形:具有特殊形状的一个图形.
成轴对称:有特殊位置关系的两个相同图形.
区别
对应线段相等,对应角相等.
把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做对称点.
06
作业布置
【知识技能类作业】必做题:
1.数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
B
2.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠D=80°,则∠BAD的度数为( )
A.170° B.150° C.130° D.110°
C
3.如图,△ABC与△A'B'C'关于直线l对称,且∠A=105°,∠C'=30°,则∠B的度数为( )
A.25° B.45° C.30° D.20°
06
作业布置
【知识技能类作业】必做题:
B
06
作业布置
【知识技能类作业】选做题:
4.将一张正方形纸片按如图步骤①②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A
5.如图,在△ABC中,点D、E分别在边AB、BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为( )
A.9 B.10 C.11 D.12
06
作业布置
【知识技能类作业】选做题:
C
6.围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,则所得的对弈图是轴对称图形.(填写A、B、C、D中的一处即可,A、B、C、D位于棋盘的格点上)
06
作业布置
【知识技能类作业】选做题:
A或C
06
作业布置
【综合拓展类作业】
7.如图,在△ABC中,将∠B、∠C按如图所示的方式折叠,点B、C均落于边BC上的点Q处,MN、EF为折痕.若∠A=82°,则∠MQE的度数为 .
82°
06
作业布置
【综合拓展类作业】
D
8.如图,弹性小球从点P出发,沿图所示的方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到长方形的边时,反弹点为Q,第2次碰到长方形的边时,反弹点为M……则第2025次碰到长方形的边时,反弹点为图中的( )
A.点P B.点Q C.点M D.点N
Thanks!
https://www.21cnjy.com/recruitment/home/fine
